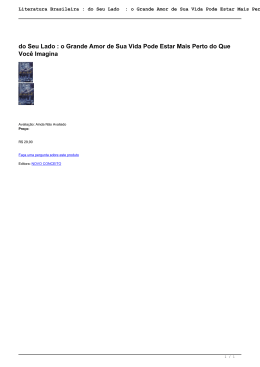
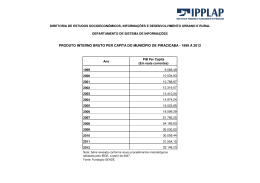
196
Revista Brasileira de Ensino de F
sica, vol. 23, no. 2, Junho, 2001
Perl de Velocidade para o Escoamento de
Fluido em uma Placa Plana
Velocity Prole fo the Fluid Flow in a Flat Plane
Katia Barros de Lacerda e A. E. A. Amorim
Faculdade de Tecnologia de Jahu, CEETEPS
CEP 17212-650, Ja
u, SP
Recebido em 21/02/2001. Aceito em 12/03/2001
Neste trabalho discutimos a abordagem feita para se estudar o conceito de camada limite usando
uma distribuic~ao polinomial para o perl de velocidade no escoamento de um uido em uma placa
plana e comparamos os resultados obtidos na literatura com um outro metodo onde a distribuic~ao
de velocidade e obtida atraves da serie de Taylor em torno da camada limite.
In this work we discuss the approach done to study the layer boundary concept using a polinomial
distribution for the velocity prole for the ow of a uid in a at plate and we compare the results
obtained in the literature with another method where the distribution of velocity is obtained trough
the series of Taylor around the boundary layer.
I
Introdu
c~
ao
Nos livros-textos de Mec^anica dos Fluidos utilizados na graduac~ao, um assunto de especial relev^ancia
para as Engenharias e a Fsica, trata sobre o escoamento de uidos atraves de corpos submersos.
De uma maneira geral, os livros abordam inicialmente o conceito de camada limite, introduzido por
Prandtl[1], em 1904, que sugeriu que a analise do escoamento do uido, em torno do objeto, pudesse ser
feito em duas regi~oes: uma proxima ao objeto onde os
efeitos do atrito s~ao muito importantes, e uma externa,
onde o atrito pode ser desprezado. O contorno que delimita estas regi~oes chama-se camada limite.
Assim, os livros abordam inicialmente o estudo do
escoamento do uido sobre uma placa plana, onde se
discute a formac~ao da camada limite. A analise qualitativa deste processo e feita usando o conceito de linha de corrente. Nas linhas adjacentes a placa, aparece uma forca de interac~ao entre o uido e a placa,
que produz uma reduca~o na velocidade de escoamento
destas linhas. Em virtude da diferenca de velocidade
entre estas linhas com as linhas de corrente adjacentes
do uido, ocorre o cisalhamento sobre um elemento de
uido tomado nesta regi~ao. A forma como ocorre o cisalhamento do uido esta associada com a viscosidade
do uido.
medida que nos afastamos da placa, o cisalhaA
mento diminui. O resultado nal e uma distribuica~o de
velocidade entre as linhas de corrente, tambem conhe-
cida como perl de velocidade. A forma analtica exata
desta distribuic~ao e desconhecida e, por esta raz~ao, s~ao
utilizadas algumas express~oes aproximadas nos livrostextos, que satisfazem as condic~oes de contorno do pro assumido que a velocidade do uido, junto
blema. E
a placa e nula. Esta e a hipotese do n~ao escorregamento. A outra condic~ao assume que a velocidade do
uido, num ponto distante da placa, e constante e igual
a velocidade do uido sem a placa.
Embora o procedimento adotado pelos livros-textos
seja muito utilizado, do ponto de vista didatico, o aluno
perde a correlac~ao existente entre os coecientes de seu
modelo matematico com as condic~oes de contorno do
problema.
Por outro lado podemos aplicar a serie de Taylor ao
perl de velocidade em torno da camada limite, utilizando as mesmas condic~oes de contorno, comparando
os resultados com as express~oes dos livros.
Neste artigo sera feita uma discuss~ao sobre estas
metodologias para se obter o perl de velocidade do
escoamento do uido atraves de uma placa plana.
Antecipando os resultados, observamos que a
soluc~ao obtida usando a expans~ao em serie de Taylor
e unica para expans~oes de primeira e segunda ordem.
Nestas ordens de expans~ao, a express~ao e valida para
camadas limites muito estreitas. Para expans~oes de terceira ordem ou superior, o resultado n~ao e unico, apresentando innitas soluc~oes dependentes dos valores dos
coecientes da serie de Taylor. O outro metodo, pelo
fato de ser polinomial n~ao apresenta restric~ao no resul-
197
K
atia Barros de Lacerda e A. E. A. Amorim
tado.
Por outro lado, observamos que os coecientes da
expans~ao est~ao relacionados com as condic~oes de contorno. Este fato permite ao aluno entender a depend^encia dos coecientes do perl de velocidade com
as condic~oes de contorno.
Finalmente, notamos que os pers obtidos s~ao
id^enticos na forma. Contudo devemos destacar que o
metodo da serie de Taylor imp~oe um regime de validade
para a aplicac~ao do perl de velocidade para camadas
limites estreitas enquanto que o metodo do polin^omio
n~ao faz qualquer restric~ao.
O trabalho esta organizado na seguinte forma: na
sec~ao seguinte discutimos algumas considerac~oes iniciais e apresentamos o modelo. Na ultima seca~o apresentamos as conclus~oes e resultados principais.
II
Camada limite
As camadas do uido, num escoamento real, t^em a
sua velocidade relativa a placa v(y) afetada por tens~oes
de cisalhamento provocadas pelas interac~oes existentes
as partculas do uido que percorrem distintas linhas de
corrente. De acordo com Prandtl, identicamos uma
regi~ao na qual o uido pode ser tratado como ideal,
ja que a velocidade relativa entre as linhas de corrente
e a mesma, e uma outra regi~ao na qual a viscosidade
desempenha um papel fundamental.
Devido ao atrito existente entre o uido e a placa,
o escoamento da camada de uido diminui ate parar.
Esta hipotese do n~ao escorregamento do uido pressup~oe que a velocidade da camada do uido na placa
e nula v (0) = 0.Evid^encias experimentais comprovam
este fato[2].
medida que nos afastamos da placa a velocidade
A
do uido cresce rapidamente ate atingir a velocidade
do escoamento inicial vo , a uma dist^ancia Æ da placa,
denindo a espessura da camada limite naquele ponto
da placa.
Nesta situac~ao a velocidade do uido e id^entica a velocidade de escoamento do uido fora da camada limite
v (Æ ) = vo .
Alguns livros assumem que a variac~ao da velocidade,
na borda da camada limite e desprezvel,
@v @y y =Æ
= 0;
(1)
utilizando tal equac~ao como condic~ao de contorno.
Contudo, devemos frisar que, em um estudo mais realista, as condic~oes de contorno est~ao restritas ao escoamento do uido junto a placa (v (0) = 0) e fora da
camada limite (v (Æ ) = vo ).
Tais resultados podem ser resumidos como mostra
a Figura 1.
Figura 1. Camada limite e o perl de velocidade do uido.
As echas indicam a magnitude da velocidade do uido. A
linha curva e tracejada representa a camada limite. A linha
curva e contnua, que delimita as echas, expressa o perl
de velocidade do uido.
Contudo, a forma exata do perl da velocidade e
desconhecida, sendo conhecido apenas os seus valores
numericos atraves da soluc~ao de Blasius[3]. Em func~ao
disto, alguns autores[3] escrevem o perl de velocidade
como uma func~ao polinomial.
Para um estudo inicial sobre a forma aproximada do
perl de velocidade, os livros-textos assumem uma distribuic~ao das velocidades como uma curva de segundo
grau na forma
v (y )
= Ay 2 + By + C;
(2)
onde A e B s~ao determinadas pelas condic~oes de contorno ja mencionadas.
Com as condic~oes de contorno impostas na Eq.2,
temos
vo
= AÆ 2 + BÆ;
(3)
= 0;
(4)
C
e
2AÆ + B = 0:
(5)
Com estes resultados, as constantes se escrevem
vo
A
=
B
=2
e
Æ2
vo
Æ
;
(6)
;
(7)
de forma que o perl de velocidade e dado por
v (y )
= vo
vo
Æ2
(Æ
2
y) :
(8)
Observe que nesta deduc~ao o resultado nal do perl expressa a depend^encia da velocidade em func~ao da
coordenada y e, a primeira vista, a Eq.8 n~ao apresenta
de forma clara a depend^encia das condic~oes de contorno
no perl de velocidade.
Para efeito comparativo iremos deduzir o perl de
velocidade usando a serie de Taylor. Considere agora
uma expans~ao do perl de velocidade em torno da camada limite, ate a segunda ordem, conservando um
ponto xo na placa, como mostra a Figura 2.
198
Revista Brasileira de Ensino de F
sica, vol. 23, no. 2, Junho, 2001
1 d2 v v (0) = 0 = vo +
Æ2 :
2 dy 2 y=Æ
por
Assim
v (y )
= vo +
dy y=Æ
1 d2 v Æ) +
(y
2 dy 2 y=Æ
(y
Æ )2 ;
Desta forma, temos que o perl de velocidade e dado
v (y )
vo
= vo
Æ2
2
(y
Æ) ;
(11)
cujo resultado coincide com a express~ao obtida anteriormente na Eq. 8 usando o metodo do polin^omio.
Contudo, a validade do resultado dado pela Eq.11 esta
restrita a camadas limites estreitas, devido a ordem de
expans~ao considerada.
Por outro lado, truncando a serie ate termos de terceira ordem e aplicando as mesmas condic~oes de contorno,
Figura 2. Expans~ao do perl de velocidade em torno de um
ponto da camada limite.
dv (10)
(9)
0 = vo +
Aplicando as condic~oes de contorno temos que o segundo termo do lado direito da equaca~o acima e nulo e
que, para y = 0,
1 d2 v Æ2
2 dy 2 y=Æ
1 d3 v Æ3 ;
6 dy 3 y=Æ
(12)
o perl de velocidade do uido se escreve
c
v (y )
= vo +
Æ 2 d2 v 2
y
1
2 dy 2 y=Æ Æ
!
+ vo +
Æ 2 d2 v 2 dy 2 y=Æ
3
y
1
Æ
(13)
:
Expandindo as pot^encias e separando as express~oes em termos de pot^encia de y=Æ o perl se escreve
!
v (y )
=
3vo +
Æ 2 d2 v 2
dy 2 vo +
Æ
y =Æ
!
Æ 2 d2 v 2 dy 2 y=Æ
d2 v 3vo + Æ 2 2 dy y=Æ
y
y 3
Æ
!
y 2
Æ
+
(14)
:
d
Observe que com series de terceira ordem ou superiores o perl de velocidade v (y ) e indeterminado, pois
depende do valor da segunda derivada da velocidade.
Desta forma, este tratamento t^em validade para camadas limites estreitas se e utilizada uma soluca~o exata.
Para ordens mais elevadas, a distribuic~ao da velocidade
ca indeterminada.
Contudo, Shames prop~oe uma soluc~ao particular
para este caso de forma que termos da segunda ordem
sejam nulos[5]. Portanto, partindo da forma polinomial, o perl de velocidade obtido e
v (y )
= vo
3y
2Æ
y3
2Æ 3
:
(15)
Este mesmo resultado e obtido, partindo da Eq.14.
Desta forma, pelo fato do coeciente de segunda ordem
ser nulo, ent~ao
d2 v dy 2 y =Æ
=
3vo
Æ2
:
(16)
Substituindo na express~ao, o perl de velocidade reduz a
y3
3y
:
(17)
v (y ) = vo
2Æ 2Æ 3
O resultado e o mesmo que o obtido por Shames,
considerando um polin^omio. Observe que em ambos
os casos estudados, as express~oes para a velocidade do
uido s~ao equivalentes, mostrando que os metodos s~ao
equivalentes. Contudo a abordagem feita utilizando
expans~ao em series de Taylor para o perl de velocidade e mais natural. Os coecientes apresentam um
conteudo fsico e matematico bem claro, ressaltando
que o limite de validade do perl depende da ordem
de grandeza considerada. Para ordens elevadas, o perl
199
K
atia Barros de Lacerda e A. E. A. Amorim
admite varias soluc~oes e a soluc~ao exata e encontrada
para camadas limites estreitas.
III
Conclus~
oes
Neste trabalho, foi efetuado um estudo sobre a
abordagem utilizada nos livros sobre o conceito do perl de velocidade para um uido escoando por uma placa
plana. A abordagem feita atraves da expans~ao do perl
de velocidade em torno da camada limite, utilizando a
serie de Taylor, torna mais clara ao aluno, permitindo
que o mesmo avalie a validade da soluc~ao obtida em
termos da ordem considerada. Termos de terceira ordem ou superior cam indeterminadas. Para termos de
segunda ordem, a soluc~ao e exata. A escolha de func~oes
polinomiais para o perl de velocidade n~ao permite que
se tenha uma ideia clara da relac~ao dos coecientes em
termos das condic~oes de contorno, alem do que n~ao
imp~oe uma restric~ao sobre a validade deste tratamento,
induzindo o estudante a crer que e valido para camadas
limites de qualquer tamanho.
Agradecimentos
Os autores agradecem o apoio nanceiro da FA-
PESP. Um dos autores (AEAA) agradece ao prof. Marcos Shoiti pela confecc~ao dos desenhos e leitura do artigo.
References

[1] L. Prandtl, L., Uber
Flussigkeitsbewengung bei sehr kleiner Reibung, Verhandl. des III Intern. Math.-Kongr.,
Heidelberg, 1904.
[2] Rui Carlos Camargo Vieira, Atlas de Mec^anica dos Fluidos, p. 109, Editora Edgard Bl
ucher Ltda. 1971.
[3] Willian S. Janna, Introduction to Fluid Mechanics, third
Ed., International Thomson Publishing, p. 697, 1993.
[4] Ennio Cruz da Costa, Mec^anica dos Fluidos, Editora
Globo, 1973.
[5] Irving H. Shames, Mec^anica dos Fluidos, Editora Edgard Blucher Ltda,Volume I e II, 1973. Traduc~ao Mauro
O.C. Amorelli.
[6] Dayr Schiozer, Mec^anica dos Fluidos, Editora Argentina,1990.
[7] Victor L. Streeter e E. Benjamin Wyllie, Mec^anica dos
Fluidos, Editora McGraw-Hill do Brasil Ltda, 1982.
Traduc~ao de Milton Goncalves Sanches.