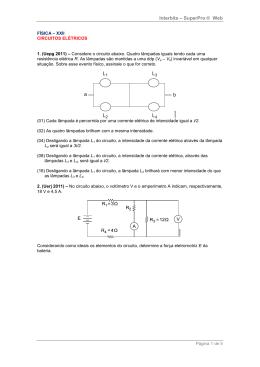
FÍSICA
Prof. Cazuza
LISTA DE EXERCÍCIOS – APOSTILA 13
1. (G1 - ifsc 2012) Um estudante do ensino médio quer montar em seu
quarto um circuito com quatro lâmpadas idênticas com a seguinte
especificação (2,0 V – 8,0 W). Mas para alimentar o circuito ele conta
somente com uma fonte (ε 20,0 V e r 1,0 ). Para não queimar as
lâmpadas ele usa um resistor R, como está indicado na figura abaixo:
Com base na situação exposta, é CORRETO afirmar que:
a) as lâmpadas vão queimar, independentemente do valor de R.
b) a resistência R vale 2,0 .
c) o objetivo do resistor R neste circuito é transformar energia elétrica em energia luminosa.
d) a resistência R vale 4,0 .
e) se o estudante associar as lâmpadas em paralelo, elas não vão queimar.
2. (Pucsp 2012) O resistor RB dissipa uma potência de 12 W. Nesse caso, a potência dissipada pelo
resistor RD vale:
a) 0,75 W
b) 3 W
c) 6 W
d) 18 W
e) 24 W
3. (Unesp 2012) Considere o circuito elétrico que esquematiza dois
modos de ligação de duas lâmpadas elétricas iguais, com valores
nominais de tensão e potência elétrica 60 V e 60 W, respectivamente.
Modo A – ambiente totalmente iluminado: a chave Ch, ligada no ponto A,
mantém as lâmpadas L1 e L2 acesas.
Modo B – ambiente levemente iluminado: a chave Ch, ligada no ponto B,
mantém apenas a lâmpada L1 acesa, com potência menor do que a
nominal, devido ao resistor R de resistência ôhmica constante estar ligado
em série com L1 .
Considerando que as lâmpadas tenham resistência elétrica constante, que os fios tenham resistência
elétrica desprezível e que a diferença de potencial de 120 V que alimenta o circuito seja constante, calcule a
energia elétrica consumida, em kWh, quando as lâmpadas permanecem acesas por 4 h, ligadas no modo A
– ambiente totalmente iluminado. Determine a resistência elétrica do resistor R, para que, quando ligada no
modo B, a lâmpada L1 dissipe uma potência de 15 W.
4. (Ufmg 2012) Arthur monta um circuito com duas lâmpadas
idênticas e conectadas à mesma bateria, como mostrado
nesta figura:
Considere nula a resistência elétrica dos fios que fazem a
ligação entre a bateria e as duas lâmpadas. Nos pontos A,
B, C e D, indicados na figura, as correntes elétricas têm,
respectivamente, intensidades iA , iB , iC e iD .
1
a) A corrente elétrica IB é menor, igual ou maior à corrente elétrica iC ? Justifique sua resposta.
b) Qual é a relação correta entre as correntes elétricas iA , iB e iD ? Justifique sua resposta.
c) O potencial elétrico no ponto A é menor, igual ou maior ao potencial elétrico no ponto C? Justifique
sua resposta.
5. (Uff 2012) Um estudante montou o circuito da figura com três lâmpadas idênticas, A, B e C, e uma
bateria de 12V. As lâmpadas têm resistência de 100 .
a) Calcule a corrente elétrica que atravessa cada uma das lâmpadas.
b) Calcule as potências dissipadas nas lâmpadas A e B e identifique o que acontecerá com seus
respectivos brilhos (aumenta, diminui ou permanece o mesmo) se a lâmpada C queimar.
6. (Uftm 2012) Assinale a alternativa que explica corretamente o funcionamento dos elementos
componentes de um circuito elétrico.
a) A resistência interna do amperímetro deve ser muito pequena, de forma a não interferir no valor da
corrente a ser medida.
b) Os fusíveis são elementos de proteção, pois não deixam passar qualquer corrente que os atinja.
c) Os resistores são elementos muito utilizados para economizar energia elétrica, pois produzem energia
térmica.
d) A capacidade de geração de energia por uma bateria termina quando sua resistência interna diminui,
esgotando-a.
e) Os receptores de um circuito elétrico convertem toda a energia elétrica recebida em energia térmica.
7. (Uerj 2011) No circuito abaixo, o voltímetro V e o amperímetro A indicam, respectivamente, 18 V e 4,5 A.
Considerando como ideais os elementos do circuito, determine a força eletromotriz E da bateria.
8. (Ifsul 2011) Um circuito elétrico é formado por uma fonte de alimentação ideal V com tensão de 12 V e
três resistores ligados conforme a figura abaixo.
Considerando-se que cada resistor tem resistência elétrica igual a 10
circuito e a potência dissipada no resistor R3 valem, respectivamente,
a) 30
e 14,4 W.
c) 15
e 14,4 W.
b) 30
e 1,6 W.
d) 15
e 1,6 W.
2
, a resistência equivalente do
GABARITO
Resposta da questão 1: B
Dados: UL = 2 V; PL = 8 W; ε = 20 V e r = 1 .
Como as lâmpadas estão em série, a tensão na associação é a soma das tensões individuais:
Uassic 4 2 8 V.
Calculando a corrente no circuito:
PL UL i
8 2 i
i 4 A.
Calculando a resistência de cada lâmpada:
UL RL i
2 RL 4
RL 0,5 .
Aplicando a lei de Ohm-Pouiillet ao circuito:
ε Req i
ε r Rassoc R i
20
R
2
1 4 0,5
R
4
5
3 R
.
Resposta da questão 2: C
Dados: E = 24 V; I = 1 A; iA = 0,5 A; PB = 12 W; iC = 0,25 A.
Como nos dois ramos superiores a corrente se divide igualmente (0,5 A em cada ramo), as resistências têm
mesmo valor. Assim: R A 8 Ω.
O resistor RB dissipa potência PB = 12 W, com corrente I = 1 A. Da expressão da potência elétrica dissipada
num resistor: PB
RB I2
12 RB 1
2
RB
Aplicando a lei de Ohm-Pouillet:
RA
E Req I
E
RB RCD I
2
RCD
12 Ω.
8
12 RCD 1
2
24
8 Ω.
A ddp nesse ramo é:
UCD RCD I 8 1
UCD
8 V.
A corrente (iD) em RD é:
iD iC I
iD 0,25 1
iD 0,75 A.
A potência dissipada em RD por ser calculada por:
PD UCD iD 8 0,75
PD 6 W.
Resposta da questão 3:
Dados: UL = 60 V; PL = 60 W = 0,6 kW; U = 120 V.
No modo A as lâmpadas estão em série e ligadas à rede de 120 V. Portanto, elas estão operando em
condições nominais, ou seja, cada uma está sob tensão de 60 V, dissipando 60 W. A energia elétrica
consumida pelas duas lâmpadas em 4 h é:
E 2 P t 2 0,06 4
E 0,48 kWh.
A resistência RL de cada lâmpada é:
RL
UL2
PL
60 60
60
RL
60
.
No modo B, a potência é PL' = 15 W. Para essa potência a corrente é:
PL'
RLi2
15
60 i2
i2 =
1
4
i
0,5.
Aplicando a lei de Ohm-Poullet para o modo B:
U
R RL i
120
R 60 0,5
R
120
60
0,5
3
R
180
.
Resposta da questão 4:
O esquema a seguir ilustra a situação:
a) Os pontos B e C estão no mesmo fio, portanto, por eles passa a mesma corrente: iB = iC = i.
b) Como as duas lâmpadas estão em paralelo e têm resistências iguais, elas são percorridas por correntes
iguais. Então:
iB = iD = i.
Essas duas correntes, iB e iD, somam-se formando a corrente iA. Assim:
iA = iB + iD = i + i
iA = 2 i. .
Portanto, a relação correta é:
iA
iB iD
.
2
c) A diferença de potencial elétrico entre dois pontos é U = R i. Como entre os pontos citados, A e C, não
há elemento resistivo algum, o potencial elétrico no ponto A é igual ao potencial elétrico no ponto C.
Resposta da questão 5:
.
a) Dados: U = 12 V; R = 100
A resistência equivalente do circuito é:
100
Req 100
Req 150 Ω.
2
Aplicando a lei de Ohm-Pouillet:
12
U RI
I
I 0,08 A.
150
Assim:
eq
iA
I
0,08 A;
iB
iC
I
2
0,04 A.
b) Calculemos as potências dissipadas para o caso do item anterior:
P
2
Ri
PA
100 0,08
PB
PC
2
0,64 W;
100 0,04
2
0,16 W.
Se a lâmpada C queimar, as lâmpadas A e B ficam em série, submetidas à tensão U’ = 6 V cada uma.
As novas potências dissipadas serão:
P
U'
2
R
PA'
PB'
62
100
0,36 W.
Comparando os valores obtidos, concluímos que o brilho da lâmpada A diminui e o brilho da lâmpada B
aumenta.
Resposta da questão 6: A
O amperímetro é um instrumento ligado em série com os demais elementos do circuito. Por isso, a sua
resistência interna deve ser desprezível em relação às demais resistências do circuito, de forma a não
alterar significativamente a resistência equivalente desse circuito, fornecendo leitura de erro desprezível.
4
Resposta da questão 7:
Dados: UCD = UBE = 18 V; i2 = 4,5 A.
1ª Solução:
No resistor R3:
UCD = R3 i3
18 = 12 i3
i3 = 1,5 A.
A corrente total é:
i = i2 + i3 = 4,5 + 1,5
i = 6 A.
Aplicando a Lei de Kirchoff na malha ABCDEFA:
E – R1 i – UCD – R4 i = 0
E = 3 (6) + 18 + 4 (6)
E = 60 V.
2ª Solução:
No resistor R3:
UCD = R3 i3
18 = 12 i3
i3 = 1,5 A.
No resistor R2:
UBE = R2 i2
18 = R2 (4,5)
R2 = 4 Ω .
A corrente total é:
i = i2 + i3 = 4,5 + 1,5
i = 6 A.
Calculando a resistência equivalente do circuito:
R 2 R3
12 4
R4
Req 3
4
Req = R1
R 2 R3
12 4
Req = 10
.
Aplicando a Lei de Ohm-Pouillet:
E = Req i
E = 10 (6)
E = 60 V.
Resposta da questão 8: D
Dados: R1 = R2 = R3 = 10 Ω ; U = 12 V.
Calculando a resistência equivalente:
R2 R3
10 10
Req R1
10
10 5
R2 R3
20
Req 15 .
Calculando a corrente total (I) no circuito:
U
12
U Req I
I
0,8 A.
Req 15
Como R2 e R3 são iguais, a corrente em cada um desses resistores é i, igual à metade da corrente total:
I 0,8
i
0,4 A.
2
2
A potência dissipada em R3 é:
P3
R3 i2 = 10 0,4
P3
1,6 W.
2
5