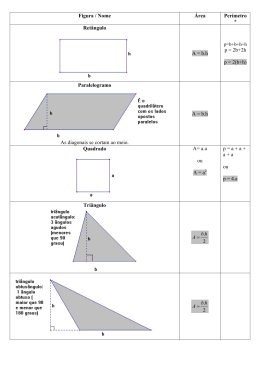
Áreas de figuras geométricas planas
Profa. Dra. Denise Ortigosa Stolf
Sumário
Página
Cálculo da área de algumas figuras planas ..................................................................... 1
Retângulo.................................................................................................................. 1
Quadrado .................................................................................................................. 1
Triângulo qualquer ................................................................................................... 1
Triângulo retângulo .................................................................................................. 1
Triângulo eqüilátero ................................................................................................. 1
Paralelogramo........................................................................................................... 1
Losango .................................................................................................................... 2
Trapézio.................................................................................................................... 2
Regiões circulares..................................................................................................... 2
Polígono regular ....................................................................................................... 2
Referências bibliográficas............................................................................................... 9
1
Áreas de figuras geométricas planas
Cálculo da área de algumas figuras planas
Retângulo
Quadrado
S = b⋅h
S = l2
Triângulo qualquer
S=
b⋅h
2
Triângulo eqüilátero
Triângulo retângulo
S=
produto das medidas dos catetos
2
Paralelogramo
S = b⋅h
S=
l2 ⋅ 3
4
2
Losango
S=
D⋅d
2
Trapézio
S=
(B + b) ⋅ h
2
Regiões circulares
Polígono regular
S = π ⋅r2
S = semiperímetro ⋅ medida do apótema
3
EXERCÍCIOS A
(1) (CESGRANRIO-RJ) Se as duas diagonais de um losango medem,
respectivamente, 6 cm e 8 cm, então a área do losango é:
a) 18 cm2
b) 24 cm2
c) 30 cm2
d) 36 cm2
(2) (CESGRANRIO-RJ) A área da sala representada na figura é:
a) 15 m2
b) 17 m2
c) 19 m2
d) 20 m2
4
(3) Na figura, há três quadrados. A área do quadrado 1 mede 16 cm2 e a área do
quadrado 2 mede 25 cm2. A área do terceiro quadrado é:
a) 36 m2
b) 40 m2
c) 64 m2
d) 81 m2
(4) (MACK-SP) A área do triângulo ABC da figura abaixo é:
a) 24
b) 12
c) 6
d) 18
e) 30
5
(5) (PUC-SP) A área do quadrado sombreado é:
a) 36
b) 40
c) 48
d) 50
(6) (FAAP-SP) Uma praça está inscrita em uma área retangular cujos lados
medem 300 m e 500 m, conforme a figura abaixo. Calculando a área da praça,
obtemos:
a) 100000 m2
b) 110500 m2
c) 128750 m2
d) 133750 m2
6
(7) (UFRGS-RS) A área do polígono da figura é 30. O lado x mede:
a) 3
b) 4
c) 5
d) 17
(8) Você quer fazer uma pipa em forma de losango, de tal forma que as varetas
meçam 75 cm e 50 cm. Nessas condições, quantos centímetros quadrados de
papel de seda você irá usar para fazer essa pipa?
7
(9) Um hexágono regular está inscrito numa circunferência de raio 18 cm.
Nessas condições, determine:
a) a medida do lado desse hexágono;
b) o semiperímetro do hexágono;
c) a medida do apótema do hexágono;
d) a área desse hexágono.
(10) (ITE-SP) A área do círculo da figura é:
a) 2π m2
b) 4π m2
c) 6π m2
d) 9π m2
8
(11) (UC-BA) Na figura abaixo temos dois círculos concêntricos, com raios
5 cm e 3 cm. A área da região sombreada, em cm2, é:
a) 9π
b) 12π
c) 16π
d) 20π
9
Referências bibliográficas
ANDRINI, Álvaro; VASCONCELLOS, Maria José. Novo praticando
matemática. São Paulo: Brasil, 2002.
BIGODE, Antonio José Lopes. Matemática hoje é feita assim. São Paulo:
FTD, 2006.
COLÉGIO ZACCARIA. Disponível em: <http:// www.zaccaria.g12.b>. Acesso
em: 12 de novembro de 2008.
DANTE, Luiz Roberto. Tudo é matemática. São Paulo: Ática, 2005.
EDIÇÕES EDUCATIVAS DA EDITORA MODERNA. Projeto Araribá:
Matemática. São Paulo: Moderna, 2007.
GIOVANNI, José Ruy; GIOVANNI JUNIOR, José Ruy. Matemática: pensar e
descobrir. São Paulo: FTD, 2005.
GIOVANNI, José Ruy; CASTRUCCI; Benedito; GIOVANNI JUNIOR, José
Ruy. A conquista da matemática. São Paulo: FTD, 1998.
GUELLI, Oscar. Matemática em construção. São Paulo: Ática, 2004.
GUELLI, Oscar. Matemática: uma aventura do pensamento. São Paulo:
Ática, 1998.
IMENES, Luiz Márcio; LELLIS, Marcelo Cestari. Matemática paratodos. São
Paulo: Scipione, 2006.
MIANI, Marcos. Matemática no plural. São Paulo: IBEP, 2006.
SÓ MATEMÁTICA. Disponível em: <http://www.somatematica.com.br>.
Acesso em: 23 de outubro de 2008.