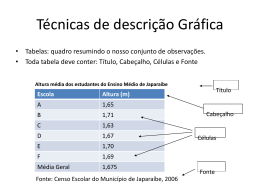
Análise Exploratória de
Dados - 2006
R - LIG-05
Objetivos da aula
Definir e calcular medidas de dispersão:
amplitude amostral, distância entre
quartis, desvio-médio, variância e desviopadrão.
Definir e calcular o coeficiente de variação
amostral.
Definir e calcular quantis de uma
distribuição de freqüências.
Exemplo 1
Suponha que um grupo de 120 estudantes
foi aleatoriamente distribuído em 6 grupos
de 20.
Cada grupo recebeu um tipo de
treinamento e depois todos foram
submetidos a um mesmo teste.
Ao teste é atribuída uma nota de zero a
10.
Exemplo 1 (continuação)
Os dados (fictícios) com as notas dos
testes para os seis grupos estão no
arquivo notas.txt.
notas=read.table(“http://www.im.ufrj/~flavia/aed06/notas.txt”)
names(notas)=c(“G1”,”G2”,”G3”,”G4”,”G5”,”G6”)
Exemplo 1 (continuação)
Calcule a média e a mediana das notas
para cada grupo.
É possível ver que todos os grupos
apresentam a mesma média 5 e a mesma
mediana 5.
Será que podemos afirmar que as
performances foram iguais para os
diferentes grupos?
> mean(notas)
G1 G2 G3 G4 G5 G6
5 5 5 5 5 5
medianaNotas<-matrix(0,1,6)
# cria o vetor medianaNotas com todas as entradas nulas
# de dimensão 1 por 6
for (i in 1:6) {medianaNotas[1,i]=median(notas[,i])}
# para i variando de 1 a 6 atribui a medianaNotas da
#coluna i a mediana das notas do i-ésimo grupo.
> medianaNotas
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 5 5 5 5 5 5
Ramo e folhas das notas
Para responder a pergunta anterior,
podemos construir os ramo-e-folhas das
notas para observar a variação das
mesmas nos diferentes grupos.
Ramo e folhas das notas
> stem(notas$G1)
5 | 00000000000000000000
> stem(notas$G2)
0 | 00
2 | 00000
4 | 000000
6 | 00000
8 | 00
> stem(notas$G3)
4 | 000000
4|
5 | 00000000
5|
6 | 000000
> stem(notas$G4,scale=2)
1 | 0000
2 | 00
3 | 00
4|0
5 | 00
6|0
7 | 00
8 | 00
9 | 0000
> stem(notas$G5)
3 | 56789
4 | 0248
5 | 00268
6 | 012345
> stem(notas$G6,scale=2)
1 | 000000
2 | 0000
3|
4|
5|
6|
7|
8 | 0000
9 | 000000
Comparação
Pelos ramos-e-folhas de cada grupo podemos
ver que há diferenças entre as respectivas
performances.
Por exemplo, no grupo 1 não houve variação:
todos os 20 estudantes obtiveram nota 5.
Já no grupo 6, nenhum estudante obteve nota 5:
ou as notas foram 1 e 2 ou 8 e 9.
Enfim, a partir deste exemplo, percebe-se a
necessidade de outras medidas para
caracterizar um conjunto de dados além de
medidas tais como média e mediana.
Medidas de Dispersão
É necessário caracterizar o conjunto
também usando medidas que avaliam a
variabilidade dos dados no conjunto.
A seguir, apresentaremos algumas
medidas de dispersão comuns.
Amplitude Amostral R
A amplitude amostral é uma das medidas
de dispersão mais simples.
É dada pela diferença entre os valores
máximo e mínimo observados na amostra.
Se x é o vetor que contém os dados,
podemos calcular a amplitude amostral
como amplitude<-max(x)-min(x).
Amplitude amostral
(continuação)
Obtenha a amplitude amostral dos
diferentes grupos.
É claro que no grupo 1 a amplitude
amostral é zero.
Vemos que nos grupos 2, 4 e 6, a
amplitude é 8; e nos grupos 3 e 5 são
respectivamente 2 e 3.
Amplitude amostral nos grupos
amplitudeNotas<-matrix(0,1,6)
# cria o vetor amplitudeNotas com entradas nulas de dimensão
# 1 por 6
for (i in 1:6) {amplitudeNotas[1,i]=max(notas[,i])-min(notas[,i])}
# atribui a cada entrada do vetor amplitudeNotas a diferença entre a
# nota máxima e mínima do respectivo grupo
> amplitudeNotas
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0 8 2 8 3 8
Desvantagens da amplitude
amostral
A grande desvantagem da amplitude
amostral como medida para caracterizar a
dispersão num conjunto de dados é que
ela só leva em conta o mínimo e o
máximo dos dados, ignorando todo o
resto.
Observe que há diferenças nos grupos 2,
4 e 6. Porém, todos eles têm a mesma
amplitude amostral.
Ramo e folhas dos grupos 2, 4 e 6
> stem(notas$G2,scale=2)
1 | 00
2|
3 | 00000
4|
5 | 000000
6|
7 | 00000
8|
9 | 00
> stem(notas$G4,scale=2)
1 | 0000
2 | 00
3 | 00
4|0
5 | 00
6|0
7 | 00
8 | 00
9 | 0000
> stem(notas$G6,scale=2)
1 | 000000
2 | 0000
3|
4|
5|
6|
7|
8 | 0000
9 | 000000
Função range()
Se x é um vetor numérico, a função
range(x) retorna o valor mínimo e o valor
máximo em x.
Assim, range(x)[2]-range(x)[1] é
equivalente à max(x)-min(x).
Amplitude interquartílica ou
Distância entre quartis (DEQ)
Uma medida de dispersão um pouco mais
refinada que a amplitude amostral é a
distância entre quartis (DEQ).
Depois de ordenada a amostra, divide-se
ela em quatro partes de freqüência
relativa ¼. Tomam-se então os valores
que correspondem à freqüência relativa
acumulada de ¼ e ¾, que são chamados
respectivamente de primeiro e terceiro
quartis (Q1 e Q3).
Distância entre quartis
DEQ=Q3-Q1
No R podemos calcular a distância entre
quartis para um vetor de dados x da
seguinte forma
deq<-IQR(x)
Para as notas do exemplo temos os
valores 0.00 4.00 2.00 6.00 2.05 8.00 para
as distâncias entre quartis dos grupos 1,
2, 3, 4, 5 e 6, respectivamente.
Valores observados de DEQ para
os diferentes grupos
DEQNotas<-matrix(0,1,6)
# cria o vetor amplitudeNotas com entradas nulas de dimensão
# 1 por 6
for (i in 1:6) {DEQNotas[1,i]=IQR(notas[,i])}
# atribui a cada entrada do vetor DEQNotas a distância entre
# quartis do respectivo grupo
> DEQNotas
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0 4 2 6 2.05 8
Distância entre quartis
(continuação)
Podemos ver que a distância entre quartis
apresenta diferenças que não foram
detectadas pela amplitude amostral entre
os diferentes grupos.
Mas, esta medida, ainda tem a
desvantagem de só levar em conta dois
valores do conjunto, ignorando os
extremos e o meio.
Função quantile(x,p)
A função quantile(x,p) retorna o quantil de
ordem p, q(p), considerando a
distribuição de freqüências dos valores no
vetor x, 0<p<1.
Assim, pedir IQR(x) é equivalente à pedir
quantile(x,0.75)-quantile(x,0.25) que
retornará Q3-Q1.
Desvio médio
É uma medida de dispersão que leva em
conta todos os valores no conjunto de dados.
Primeiro vamos definir desvio absoluto da
média.
Se x1,x2,...,xn são os valores observados e x
é a correspondente média aritmética, então um
desvio absoluto da média é dado por:
xi  x
Desvio médio
O desvio médio absoluto (DMA) é definido como a
média aritmética dos desvios absolutos da média no
vetor x, isto é,
DMA 
1
n
|x

n
i
i 1
x|
Desvio médio absoluto
dma<-c(0,0,0,0,0,0)
#atribui à dma um vetor nulo de dimensão 6
for (i in 1:6){for (j in 1:20){dma[i]<-dma[i]+abs(notas[j,i]-mean(notas[,i]))}}
#acumula em cada grupo (i variando de 1 a 6) os desvios absolutos da média
#(j variando de 1 a 20)
dma<-dma/20
#calcula a média, dividindo por 20 que é o número de notas em cada
#grupo
Desvios médios no exemplo
Para as notas nos seis grupos podemos
ver que os desvios médios são,
respectivamente,
0.00 1.80 0.60 2.70 0.91 3.60
Variância amostral
É a média dos desvios da média tomados
ao quadrado.
Veremos na disciplina Introdução à
Estatística, que no caso particular da
variância, é comum adotar o denominador
da média em n-1.
O R possui uma função própria para
calcular a variância com denominador n-1
dada por var(x), se x é o vetor contendo
os valores cuja variância está para ser
calculada.
Variância amostral
s 
2
1
n
(x

n 1
i
i 1
 x)
2
Variância de notas
Neste exemplo, temos para os grupos,
respectivamente, as variâncias
(arredondadas para duas casas decimais):
0.00 5.47 0.63 9.58 1.11 13.89
>vetVar<-c(0,0,0,0,0,0)
#vetVar é criado como um vetor #nulo de dimensão 6
>for (i in 1:6){vetVar[i]<-var(notas[,i])}
#cada entrada de vetVar recebe a variãncia amostral do
#grupo correspondente
> vetVar
[1] 0 5.473684 0.631579 9.578947 1.114737 13.894737
Desvio-padrão
É a raiz quadrada positiva da variância:
sqrt(var(x)) ou sd(x).
Neste exemplo temos os seguintes
desvios-padrão (arredondados para duas
casas decimais): 0.00 2.34 0.79 3.09 1.06
3.73
> sqrt(vetVar)
[1] 0 2.3395906 0.7947194 3.0949875 1.0558110 3.7275645
Resumo
Grupo
R
DEQ
s2
DMA
s
1
0
0
0
0
0
2
8
4.00
1.80
5.47
2.34
3
2
2.00
0.60
0.63
0.79
4
8
6.00
2.70
9.58
3.09
5
3
2.05
0.91
1.11
1.06
6
8
8.00
3.60
13.89
3.73
Histogramas na escala das freqüências
Histogramas com as escalas uniformizadas
Coeficiente de Variação
Amostral
É uma medida da variação relativa em um
conjunto de valores numéricos.
Costuma ser expresso em termos
percentuais.
Mede a dispersão dos dados em relação à
média aritmética.
É definido por CV=(DP/média)x100%,
onde DP é o desvio-padrão dos dados,
média é a média aritmética dos dados.
Exemplo 2: Considere os três
conjuntos de dados abaixo:
A
B
C
12
4.65
551
15
11.65
554
23
10.65
555
22
11.65
562
23
0.65
562
16
3.65
561
Exemplo 2: (cont.)
Os comandos estão em exemplo2.txt
Calcule a variância de cada um dos três conjuntos de dados.
dadosA<-c(12,15,23,22,23,16)
dadosB<-c(0.65,3.65,11.65,10.65,11.65,4.65)
dadosC<-c(551,554,555,562,562,561)
var(dadosA)
mean(dadosA)
22.7
18.5
var(dadosB)
mean(dadosB)
22.7
7.15
var(dadosC)
mean(dadosC)
22.7
557.5
Exemplo 2: (cont.)
dotchart(dadosA,main="A")
dotchart(dadosB,main="B")
dotchart(dadosC,main="C")
Exemplo 2: coeficiente de
variação
CV para o conjunto A:
sqrt(var(dadosA))*100/mean(dadosA) 25.75%
CV para o conjunto B:
sqrt(var(dadosB))*100/mean(dadosB) 66.66%
CV para o conjunto C:
sqrt(var(dadosC))*100/mean(dadosC) 0.85%
Conclusão: O conjunto C é o que apresenta
menor variabilidade relativa à média.
Quantis de uma distribuição de
freqüências
Tanto a média como o desvio-padrão
podem não ser medidas adequadas para
representar um conjunto de dados, pois:
(i) são afetados, de forma exagerada por
valores extremos;
(ii) apenas com estes dois valores não
temos idéia da simetria ou assimetria da
distribuição dos dados.
Quantis de uma distribuição de
freqüências (2)
Por exemplo, vimos que a mediana é
o valor que deixa 50% dos dados
(depois de ordenados) abaixo dela e
50%, acima dela.
Analogamente, podemos definir
outras medidas, variando o
percentual 50% (abaixo e acima de),
para um percentual qualquer.
Quantis de uma distribuição de
freqüências (3)
De um modo geral, podemos definir uma
medida chamada QUANTIL de ordem p,
com p representando uma proporção
qualquer, 0<p<1, tal que 100p% das
observações sejam menores do que o
quantil de ordem p.
NOTAÇÃO: q(p)
Quantis Especiais: QUARTIS
São três medidas (Q1, Q2 e Q3) que repartem a
distribuição em quatro intervalos de freqüência
relativa ¼:
q(0,25),q(0,50) e q(0,75)
q(0,25): primeiro quartil (Q1) ou vigésimo-quinto
percentil;
q(0,50): segundo quartil (Q2), ou mediana ou
qüinquagésimo percentil;
q(0,75): terceiro quartil (Q3) ou septuagésimoquinto percentil.
Quantis Especiais: DECIS
São 9 medidas que repartem a distribuição em
10 intervalos de freqüência relativa 1/10:
q(0,1),q(0,2),q(0,3),...,q(0,9)
q(0,1): primeiro decil (D1) ou décimo percentil;
q(0,2): segundo decil (D2), ou vigésimo
percentil;
q(0,3): terceiro decil (D3), ou trigésimo percentil;
etc.
Quantis Especiais: PERCENTIS
q(0,01),q(0,02),q(0,03),...,q(0,99)
q(0,01): primeiro percentil;
q(0,02): segundo percentil;
q(0,03): terceiro percentil;
etc.
Determinação dos quantis usando
oR
A função apropriada do R para obter os
quantis de um vetor numérico x é a função
quantile.
Se x é o vetor contendo os dados, e
desejamos determinar os três quartis,
pedimos quantile(x,c(0.25,0.5,0.75)).
Se desejamos o quinto e o nonagésimoquinto percentis, pedimos
quantile(x,c(0.05,0.95)), etc.
Exemplo 3: Emissão de Dióxido
de Carbono
Os dados no arquivo dados13bm.txt
fornecem emissões de dióxido de carbono
"per capita", para uma amostra de 72
países. Os dados são do ano de 1995.
Fonte: Stabilizing The Atmosphere:
Population, Consumption and Greenhouse
Gases.
Exemplo 3: Emissão de Dióxido
de Carbono (cont.)
Determine os três quartis, os decis, a
média e o desvio-padrão das emissões
registradas para os 72 países em 1995.
Exemplo 3: Emissão de Dióxido
de Carbono (cont.)
dados=read.table(”http://www.im.ufrj/~flavia/aed06/dados13bm.txt",header=T)
names(dados)
[1] "pais" "emissao"
quantile(dados$emissao,c(0.25,0.5,0.75))
25% 50% 75%
0.0675 0.4150 1.4725
quantile(dados$emissao,c(0.1,0.2,.3,.4,.5,.6,.7,.8,0.9))
10% 20% 30% 40% 50% 60% 70% 80% 90%
0.02 0.05 0.14 0.28 0.42 0.87 1.26 1.99 3.02
Exemplo 3: Emissão de Dióxido
de Carbono (cont.)
> mean(dados$emissao)
[1] 1.174167
> sqrt(var(dados$emissao))
[1] 1.689093
Histograma das emissões
Quantis para dados agrupados
Uma aproximação para obter o quantil de ordem p
quando os dados estão agrupados em classes é a
seguinte.
Passo 1: Encontre a classe que contém o p-quantil.
Seja [ap,ap+1[ esse intervalo e Fp a freqüência relativa
acumulada desta classe.
Passo 2: Encontre o comprimento desse intervalo (cp),
a freqüência relativa dessa classe (fp) e a freqüência
relativa acumulada da classe anterior (Fp-1).
Passo 3: Calcule q(p) como
cp
q( p)  a p 
( p  Fp 1 )
fp
Quantis para dados agrupados
q( p)  a p 
(ap,ap+1) - classe que contém
q(p);
Fp - freqüência relativa
acumulada da classe (ap,ap+1)
cp – a amplitude da classe
fp – a freqüência relativa da
classe e
FP-1- freqüência relativa
acumulada da classe
imediatamente anterior
cp
fp
 ( p  Fp 1 )
Atividade
Trabalhe com os dados sobre
temperaturas médias mensais de
Cananéia e Ubatuba no estado de São
Paulo.
Selecione as temperaturas de janeiro,
para as duas cidades, ao longo dos anos
estudados.
Determine os quartis das temperaturas
médias de janeiro para as duas cidades
Atividade (continuação)
Repita a atividade anterior para os outros
meses do ano.
Faça um resumo dos resultados obtidos
numa tabela e num gráfico.