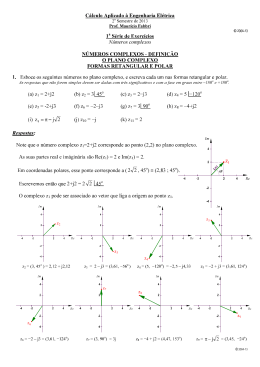
Combinação de Elementos de Simetria
Para descrever a simetria externa de qualquer cristal temos
32 grupos pontuais.
m
1
1 2 3 4 6 2 3 4 6
+ 22 combinações
Apenas 22 combinações porque muitas combinações se
repetem e algumas são impossíveis nos sistemas
cristalinos.
Combinação de um eixo de rotação
com o centro de inversão
n impar
n
n par
n/m
n + i
Temos então 3 novos grupos pontuais.
2
+
1
4 +
1
6 +
1
Combinação de eixos de rotação
A combinação de apenas 2 eixos de simetria é impossível, pois se dois
eixos se combinam pelo menos um terceiro eixo passará pelo ponto
comum entre eles.
z/2
A Figura ao lado ilustra o triângulo esférico ( em
vermelho) formado pelos eixos X, Y e Z na superfície
de uma esfera.
X
x/2
Z
Y
Como a soma dos ângulos do triângulo esférico (x/2,
y/2 e z/2) deve ser maior que 180o mas não pode
exceder 540o:
180 
o
y/2
x
2

y
2

z
2
 5400
Sabendo que x , y e z são os graus de giro dos eixos
X, Y e Z respectivamente, pode ser demonstrado
matematicamente que as combinações possíveis para X,
Y e Z são: 222, 322, 422, 622, 432 e 233.
Através da aplicação da lei dos cosenos para triângulo esférico
podemos obter os ângulos formados pelos eixos X, Y e Z
X
Y
Z
X^Y
X^Z
Y^Z
2
3
2
2
2
2
90o
90o
90o
90o
90o
60o
4
2
2
90o
90o
45o
6
2
2
90o
90o
30o
4
3
2
54o44’
45o
35o16’
2
3
3
54o44’
54o44’
72o32’
4
Perpendicular
às faces
3
2
Meio de arestas
opostas
Diagonal de
corpo
Guia do cubo
2
3
Meio de arestas
opostas
Perpendicular
às faces
Diagonal
de corpo
Não tem
simetria