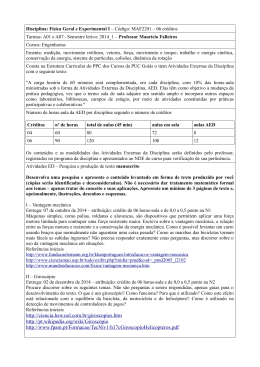
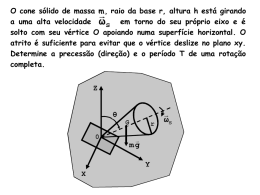
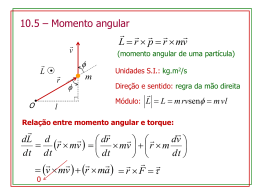
Ensaio Laboratorial de Mecânica Aplicada 2
Movimento Giroscópico
1. Introdução
O giroscópio consiste num disco solidário com um
eixo normal que, por sua vez, está montado num
aro, num plano transversal do disco que, por sua
vez, pode girar em torno de outro eixo, no plano
longitudinal.
O giroscópio foi inventado em 1850 por Jean
Bernard Léon Foucault (1819 - 1868), que o
utilizou para mostrar que a Terra, de facto, gira
sobre seu próprio eixo.
A rotação do disco a alta velocidade confere ao
mecanismo duas propriedades importantes que o tornam bastante útil, em diversas
aplicações:
- a primeira resulta do facto de o vector do momento angular resultante ser
constante e ter a direcção do eixo de suporte do disco, quando este não está
sujeito a momentos. Portanto, o eixo do giroscópio tem uma direcção invariável no
espaço, em relação a um referencial de inércia. Assim, se o eixo estiver na
horizontal, ele efectuará, aparentemente, uma revolução no sentido contrário à
rotação da Terra. O movimento é aparente porque a direcção do eixo é invariável e
o que roda é a Terra. Esta propriedade permitiu Foucault mostrar que a Terra roda
em torno do seu próprio eixo. Esta propriedade justifica a utilização em plataformas
de inércia, giro-bússulas e outros instrumentos de navegação, dando-se, como
exemplo, o aparelho de Aubry que estabiliza o movimento de um torpedo num
plano horizontal, em que o eixo do giroscópio coincide com a direcção do alvo. Se
o torpedo, num dado instante, é desviado do seu percurso, o giroscópio, ao
retomar a direcção original, actua, através de mecanismos reguladores, sobre o
leme do torpedo, obrigando este a retomar a direcção pré-estabelecida.
- a segunda, denominada precessão, é observada, por
exemplo, quando o giroscópio é sujeito a uma rotação
que tende a alterar a direcção do seu eixo. Quando a
intersecção dos dois eixos, o de rotação e o do
referencial, não coincide com o centro de gravidade, o
eixo do giroscópio descreve uma trajectória cónica em
torno do outro eixo. Este movimento denomina-se
movimento de precessão e pode ser observado no
movimento de um pião. Esta propriedade também
pode ser observada no giroscópio onde a intersecção
dos eixos coincide com o centro de gravidade, mas está sujeito a um momento de
torção aplicado no eixo transversal ao disco. Então, o giroscópio efectua um
movimento de precessão em torno do eixo longitudinal. A velocidade do
movimento de precessão é proporcional ao momento aplicado. Se fizermos a
comparação com o que se passa com a aplicação do mesmo momento a um corpo
que não se encontra em rotação, o corpo roda com uma aceleração angular
proporcional ao momento aplicado. Se retirarmos o momento, o corpo continua em
movimento. Quando o momento deixa de
actuar
no
precessar.
giroscópio,
ele
Um
exemplos
dos
deixa
de
de
fenómenos de precessão na Natureza é o
da precessão de equinócios da Terra. Se a
Terra
fosse
perfeitamente
esférica,
nenhum dos outros membros do sistema
solar
exerceria
qualquer
momento
gravitacional. Mas, a Terra não é uma
esfera perfeita e, por isso, principalmente
o Sol (pelo seu tamanho) e a Lua (pela
sua proximidade) exercem um momento
de torção gravitacional sobre ela, provocando o movimento de precessão do seu
eixo, com uma velocidade de 50,25”/ano, ou seja, uma rotação completa em cerca
de 26000 anos.
O trabalho experimental a ser realizado no Laboratório de Mecânica Aplicada
utiliza um giroscópio didático que permite observar as propriedades deste
mecanismo e tem, por finalidade, comprovar que existe uma relação de
proporcionalidade entre o momento de torção aplicado num dos eixos e a
velocidade de precessão e que essa relação é o momento angular.
2. Descrição sumária do equipamento
O giroscópio, que vai ser utilizado neste trabalho experimental, possui um disco de
150 mm de diâmetro montado num veio de um motor de baixa inércia. O disco está
montado com um anel removível. O motor está rigidamente ligado a uma protecção
do disco que, com dois pinos bloqueadores, formam o aro interior que, por sua
vez, está ligado por dois semi-eixos a um suporte em forma de “U”. Este suporte
constitui o aro exterior e é suportado por rolamentos numa coluna vertical, de
forma a poder girar livremente
sobre esta.
Ligados ao aro interior, encontram-se dois
braços de extensão calibrados, nos quais é
possível colocar três massas de 150 g, cada,
a fim de produzirem um momento externo,
em relação ao eixo transversal. Se o anel,
que
se
encontra
ligado
ao
disco,
for
removido, então o aro interior deverá ser
calibrado através da colocação da massa de
50 g no braço de extensão que lhe está
ligado.
O giroscópio e a coluna estão montados num
conjunto de alimentação que fornece potência eléctrica de corrente contínua e
voltagem variável ao motor que acciona o giroscópio e que permite que a sua
velocidade de rotação varie até cerca de 5000 rpm. Trocando a polaridade da
alimentação eléctrica é possível inverter o sentido de rotação do motor. A
velocidade do disco do giroscópio pode ser medida com precisão, através do
tacómetro óptico. Para medir a velocidade de precessão, é necessário instalar um
dispositivo de fim-de-curso.
3. Teoria
3.1 Lista de símbolos
h = momento angular
J = momento polar de inércia em relação a X-X
k = raio de giração
l = comprimento do cilindro
kg m2/s
kg m2
m
m
m = massa
r = raio do cilindro
dt = tempo de processão no ângulo i
ρ = densidade
τ = momento de torção aplicado
di = ângulo de precessão no tempo t
ω = velocidade de rotação no eixo X-X
Ω = velocidade de precessão em Z-Z
kg
r
s
kg/m3
Nm
radianos
rad/s
rad/s
3.2 Introdução Teórica
A
figura
representa,
esquemáticamente,
o
disco de um giroscópio
e do motor a que está
acoplado, que roda em
torno do eixo X-X com
uma velocidade angular,
ω.
Se o momento polar de
inércia do conjunto rotor em relação ao eixo X-X for J, então o momento angular
em relação ao eixo de rotação X-X é h = Jω, que pode ser representado pelo
vector ab.
Se se aplicar um momento de torção, τ , ao aro interior, no eixo
determinado período de tempo,
relação ao eixo
z-z,
y-y,
num
δt, haverá uma variação do momento angular em
igual a τ dt, representado pelo vector, bc, que fará o eixo
descrever um ângulo δθ. Este movimento do eixo é denomidada por precessão.
A partir da triangulação dos vectores abc, é possivel concluir que
τ dt = Jω dθ
(1)
ou
dθ
dt
(2)
= JωΩ
(3)
τ = Jω
= hΩ
em que Ω =
(4)
dθ
, ou seja, a velocidade angular de precessão.
dt
Portanto, se a velocidade do disco for constante, existe uma relação proporcional
entre o momento de torção e a velocidade de precessão. Observa-se, também,
que a constante de proporcionalidade é função do momento polar de inércia. A
demonstração experimental destas relações constitui o objectivo deste trabalho.
3.3 Dimensões
As dimensões do disco rotor do giroscópio e do anel removível são indicadas na
figura:
O material do disco e anel é latão de densidade, ρ, igual a 8410 kg/m3.
4. Experiência
4.1 Equipamento
O trabalho experimental será realizado com o seguinte equipamento:
- um Giroscópio eléctrico Cussons P5377
- um tacómetro óptico Cussons P4740
4.2 Procedimento
Os alunos irão encontrar o giroscópio equilibrado. A sua equilibragem deve ser
efectuada da seguinte forma:
4.2.1 - Colocar a massa de 50 g no braço de extensão do aro interior do lado
do motor. Desapertar o parafuso de fixação para libertar o aro interior do aro
exterior. Ajustar a posição da massa de 50 g na extensão até que o giroscópio
esteja equilibrado relativamente ao eixo y-y.
4.2.2 – Segurar um dos braços de extensão de modo a que o eixo rotativo
esteja na horizontal e rodar, simultaneamente, o controlo de velocidade no
sentido dos ponteiros do relógio até que seja alcançada a velocidade desejada.
Medir a velocidade de rotação com o tacómetro óptico.
4.2.3 – Libertar o braço de extensão com o eixo rotativo na horizontal e se
necessário ajustar a posição a massa de equilíbrio de 50 g de modo a que o
giroscópio permaneça horizontal e não rode em torno do eixo z-z.
Portanto, o trabalho a realizar pelos alunos consistirá em:
4.2.4 – Prender um dos braços de extensão e colocar uma massa de 150 g no
braço de extensão do aro interior na marca de 20 cm e libertar o braço de
extensão com o eixo rotativo na horizontal e medir o período de precessão e a
direcção de precessão. Medir a velocidade do giroscópio.
4.2.5 – Repetir o procedimento do parágrafo anterior movendo a massa para
distâncias diferentes da coluna vertical. Efectuar mais leituras adicionando uma
segunda e uma terceira massa, no braço de extensão.
4.3 Tratamento dos Resultados
4.3.1 – Preencher a folha de cálculo, em anexo.
4.3.2 – Trace um gráfico do momento aplicado, τ ,em função do produto das duas
velocidades,
ω Ω , fazendo passar uma recta pelos pontos. Determine
graficamente o valor do momento polar de inércia.
4.3.3 – Determine a intersecção da recta, na origem das abcissas (ou seja, para
velocidade de precessão igual a zero).
4.3.4 - Calcule o momento polar de inércia do disco e do anel e do conjunto motor
e compare com o valor obtido experimentalmente.
4.4 Discussão dos Resultados
A partir do tratamento dos resultados, tece as considerações que considere
pertinentes.
5. Bibliografia
P5377 Mk.2 Electrical Gyroscope Instruction Manual, Cussons Technology Ltd.,
2002.
Goldstein, H., Poole, C., Safko, J., Classical Mechanics, Addison Wesley, 3º ed.,
2000, pag. 223.
Targ, S., Curso Teórico-Prático de Mecânica, Ed. MIR, 1ª ed. 1974, 433-439.
Anexo
Posição do
peso 1
Posição do
peso 2
Posição do
peso 3
Momento
de Torção
Velocidade
do rotor
Período de
Precessão
Velocidade de
Precessão
cm
cm
cm
τ
Nm
ω
r.p.m
Τ
sec
Ω = 60/Τ
r.p.m.