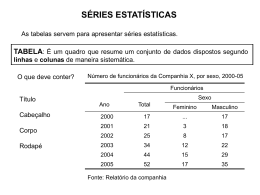
Matemática
Professora Ana Paula Medeiros
[email protected]
Estatística
Aula 1
O que é a Estatística?
É uma parte da Matemática que
fornece métodos de coleta, organização,
descrição, análise e interpretação de
dados.
Exemplos de utilização da estatística

Para calcular o índice do custo de vida, afim de determinar o índice de inflação
em certo período, inicialmente colhemos os dados sobre a variação dos
preços nesse período e, em seguida, organizamos esses dados para,
analisando-os, poder determinar o índice desejado.

Para fazer projeções sobre o número de habitantes que o planeta terá em
2020, precisamos primeiro obter os dados sobre o crescimento da população
nos últimos anos, depois organizar esses dados e, finalmente, analisá-los
para chegar à projeção desejada.

Em uma pesquisa, para determinar a intenção de voto numa eleição para
prefeito de certa cidade, em primeiro lugar colhemos os dados, ou seja, a
intenção de voto de uma parcela previamente escolhida da população, em
segundo lugar organizamos esses dados e, por ultimo, fazemos uma análise.
1. Conceitos Básicos





População
Amostra
Dado Estatístico
Divisão da Estatística
Variáveis
1.1 População
É o conjunto de elementos (pessoas, coisas,
objetos).
Exemplos: os usuários de um plano de saúde, os
membros de uma equipe de futebol, os funcionário
de uma empresa, os eleitores de um município,
estado ou pais, os alunos de uma escola, os
associados de um sindicato, os integrantes de uma
casa e várias situações que envolvem um grupo
geral de elementos.
Na estatística a população é
classificada como finita ou infinita.


População finita: Nesse caso o número de
elementos de um grupo não é muito grande,
a entrevista e análise de informações devem
abordar a todos do grupo.
População infinita: O número de elementos
nesse caso é muito elevado, sendo
considerado infinito.
Exemplos de População
Exemplo 1: Relativamente à população constituída
pelos alunos do ensino técnico matriculados na ACM,
podemos estar interessados em estudar as seguintes
características populacionais:
- Altura (em cm) dos alunos: Depois de medir a
altura de cada aluno, obteríamos um conjunto de
dados com o seguinte aspecto:
175, 161, 158, 156, 163, ... ,185, 139, 162
- Notas obtidas na disciplina de Estatística:
7,5; 9; 2,5; 10; 8,5; ...
Exemplos de População
Exemplo 2: Conjunto das temperaturas (em graus),
num determinado dia às 9h, em todas as cidades da
Europa: 12 ,8, 15, 4, 10, 11, 13, 12, ... , 14, 12, 10, 11
Por vezes, identifica-se População com a
característica populacional que se pretende estudar.
Relativamente ao exemplo 1, falamos da:
- População das alturas dos alunos do ...
-População das notas em Estatística ...
Relativamente ao exemplo 2, falamos da:
- População das temperaturas às 9h ...
População
Nem sempre é possível estudar exaustivamente todos
os elementos da população!
Porquê?
Pode o estudo da população ser muito exaustivo.
Exemplo: Sondagens exaustivas de todos os eleitores, sobre determinado
candidato.
Quando não é possível estudar, exaustivamente, todos
os elementos da população, estudam-se só alguns
elementos, a que damos o nome de Amostra.
1.2 Amostra
Conjunto de dados ou observações,
recolhidos a partir de um subconjunto da
população, que se estuda com o objetivo
de tirar conclusões para a população de
onde foi recolhida.
Exemplos de Amostra
Exemplo 1: Relativamente à população das alturas dos alunos do curso técnico da ACM,
consideremos a seguinte amostra, constituída pelas alturas (em cm) de 20 alunos
escolhidos ao acaso: 145, 163, 157, 152, 156, 149, 160, 157, 148, 147, 151, 152, 150,
148, 156, 160, 148, 157, 153, 162
Exemplo 2:
É importante a fase de recolhimento de
dados da amostra?
Sim, pois a amostra deve ser tão representativa quanto
possível da População que se pretende estudar, uma vez que
vai ser a partir do estudo da amostra, que vamos tirar
conclusões para a População.
Quando a amostra não representa corretamente a
população sua utilização pode dar origem a interpretações
erradas, como se sugere no seguinte exemplo:
Utilizar uma amostra constituída pelos leitores habituais de
determinada revista especializada, para tirar conclusões sobre
a população geral.
1.3 Dado Estatístico
É sempre um número real.

Primitivo ou Bruto: Número direto.

Elaborado ou secundário: porcentagem,
média, ...
1.4 Divisão da Estatística

Estatística Descritiva.

Estatística Indutiva.
Divisão da Estatística



Estatística Descritiva é a que tem por
objetivo descrever os dados observados,
tendo as seguintes atribuições.
A obtenção ou coleta de dados.
A organização dos dados.
A representação dos dados.
Divisão da Estatística
Estatística Indutiva é a parte da estatística que
tem por objetivo obter e generalizar
conclusões para a população a partir de uma
amostra, através do cálculo de probabilidade.
As tais conclusões estão sempre associados a
um grau de incerteza e consequentemente a
uma probabilidade de erro.
1.5 Variáveis
Uma variável é uma característica de um
elemento observado (pessoa, objeto ou
animal). Podendo ser:

Qualitativa

Quantitativa
Variáveis
Qualitativa: quando seus valores são
expressos por atributos.
Exemplo: Sexo (masculino ou feminino), cor
da pele (branca, preta, amarela, vermelha,...),
designação de emprego, ...
Variáveis


Quantitativa: quando seus valores são expressos
em números.
Exemplos: salários dos operários, idade dos alunos
de uma escola, número de filhos, renda anual, peso,
altura, ...)
Variável Quantitativa Discreta : é expressa por
número inteiro. Ex: 5
Variável Quantitativa Contínua : é expressa por
números decimais. Ex: 5,25
"Os campos de aplicação da Estatística
são muitos e os mais variados."
Estudos de mercado
O gerente de uma fábrica de detergentes pretende lançar um
novo produto para lavar a louça, pelo que, encarrega uma
empresa especialista em estudos de mercado de "estimar" a
porcentagem de potenciais compradores desse produto.
População:conjunto de todos os agregados familiares do País
Amostra:conjunto de alguns agregados familiares, inquiridos
pela empresa
Problema:pretende-se, a partir da porcentagem de respostas
afirmativas, de entre os inquiridos sobre a compra do novo
produto, obter uma estimativa do número de compradores na
População.
"Os campos de aplicação da Estatística
são muitos e os mais variados."
Medicina
Pretende-se estudar o efeito de um novo
medicamento para curar determinada doença. É
selecionado um grupo de 20 doentes, administrandose o novo medicamento a 10 desses doentes
escolhidos ao acaso e o medicamento habitual aos
restantes.
População:conjunto de todos os doentes com a
doença que o medicamento a estudar pretende tratar.
Amostra:conjunto dos 20 doentes selecionados
Problema:pretende-se, a partir dos resultados
obtidos, realizar um "teste de hipóteses" para tomar
uma decisão sobre qual dos medicamentos é melhor.
"Os campos de aplicação da Estatística
são muitos e os mais variados."
Controle de Qualidade
O administrador de uma fábrica de parafusos pretende
assegurar-se de que a porcentagem de peças
defeituosas não excede um determinado valor, a partir
do qual determinada encomenda poderia ser rejeitada.
População:conjunto de todos os parafusos fabricados
ou a fabricar pela fábrica, utilizando o mesmo processo.
Amostra:conjunto de parafusos escolhidos ao acaso de
entre o lote de produzidos.
Problema:pretende-se, a partir da porcentagem de
parafusos defeituosos presentes na amostra, "estimar" a
porcentagem de defeituosos em toda a produção.
"Os campos de aplicação da Estatística
são muitos e os mais variados."
Pedagogia
Um conjunto de pedagogos desenvolveu uma técnica nova
para a aprendizagem da leitura, na escola primária, a qual,
segundo dizem, encurta o tempo de aprendizagem
relativamente ao método tradicional.
População:conjunto de todos os alunos que entram para a
escola primária, sem saber ler.
Amostra:conjunto de alunos de algumas escolas selecionadas
para este estudo. Os alunos foram separados em dois grupos
para se aplicarem as duas técnicas em confronto.
Problema:do estudo da amostra, decidir qual a técnica melhor.
2. Arredondamento De Dados
De acordo com a resolução 886/66 da
Fundação IBGE, o arredondamento é feito
da seguinte maneira:

Quando o primeiro algarismo a ser
abandonado é 0, 1, 2, 3 ou 4, fica inalterado
o ultimo algarismo a permanecer.
Exemplo: 53,224 passa a ser 53,22
Arredondamento De Dados

Quando o primeiro algarismo a ser
abandonado é 6, 7, 8 ou 9, aumenta-se de
uma unidade o algarismo a permanecer.
Exemplos:
42,878 passa a 42,88
25,008 passa a 25,01
53,999 passa a 54,00
Arredondamento De Dados

Se o 5 for o ultimo algarismo ou se ao 5 só
seguirem os zeros, o último algarismo a ser
conservado só será aumentado de uma
unidade se for impar.
Exemplo:
24,775 passa a 24,78
24,565 passa a 24,56
24,46500 passa a 24,46
3. Apresentação De Dados Estatísticos


Tabular
Séries Estatísticas
3.1 Apresentação Tabular
A apresentação de dados estatísticos na
forma tabular consiste na reunião ou
grupamento dos dados em tabelas ou
quadros com a finalidade de apresentá-los
de modo ordenado, simples e de fácil
percepção e com economia de espaço.
3.1.1. Principais Elementos de uma
Tabela






Título: Conjunto de informações, respondendo às perguntas: O
quê? Onde? Quando?
Cabeçalho: Parte superior da tabela que especifica o conteúdo
das colunas.
Coluna indicadora: Parte da tabela que especifica o conteúdo
das linhas.
Linhas: Retas imaginarias que facilitam a leitura, no sentido
horizontal, de dados que se inscrevem nos seus cruzamentos
com as colunas.
Casa ou célula: espaço destinado a uma ao número.
Rodapé: são mencionadas a fonte se a série é extraída de
alguma publicação.
3.1.2. Componentes Básicos
Em termos genéricos, uma tabela se compõe dos seguintes
elementos básicos:
Título
Cabeçalho
Indicadora
De
Coluna
C
o
Casa l Linha
u
n
A
Rodapé
Componentes Básicos
Exemplo:
Brasil - Estimativa de População 1970 - 76
Ano
População (1000)
1970
93.139
1971
95.993
1972
98.690
1973
101.433
1974
104.243
1975
107.145
1976
110.124
Fonte: Anuário Estatístico do Brasil
3.2. Séries Estatísticas




As séries estatísticas consistem na apresentação
das informações (variáveis estatísticas) em formas
de tabelas, objetivando sintetizar os dados
estatísticos observados e tornando-os mais
compreensivos. Classificação das séries
estatísticas:
Séries Temporais ou Cronológicas
Séries Geográficas
Séries Específicas
Séries Composta ou Mista
Séries Temporais ou Cronológicas
São aquelas nas quais os dados são reunidos segundo o tempo que varia,
permanecendo fixos o local e a espécie.
Exemplo:
Produção de petróleo bruto - Brasil 1966 - 1970
Anos
Quantidade (cm³)
1966
6.748.889
1967
8.508.848
1968
9.509.639
1969
10.169.531
1970
9.685.641
Fonte Brasil em dados
Séries Geográficas
São aquelas nas quais os dados são reunidos segundo o local que varia
permanecendo fixos o tempo e a espécie.
Rebanho bovinos - Brasil 1970
Regiões
Bovinos
Norte
2.132
Nordeste
20.194
Sudeste
35.212
Sul
18.702
Centro-oeste
15.652
Fonte Brasil em dados
Séries Específicas
São aquelas nas quais os dados são reunidos segundo a
espécie que varia permanecendo fixos o tempo e o local.
Produção pesqueira - Brasil 1969
Itens
Produção (ton.)
Peixes
314
Crustáceos
62
Moluscos
3
Mamíferos
12
Fonte Brasil em dados
Séries Composta ou Mista
É a combinação de dois ou mais fundamentais de séries estatísticas.
Evolução do transporte de carga marítimas nas 4
Bacias
principais bacias - Brasil 1968 - 1970
Anos
1968
1969
1970
Amazônica
233.768
324.350
316.557
Nordeste
16.873
20.272
20.246
Prata
177.705
203.966
201.464
São Francisco
53.142
48.667
57.948
Fonte Brasil em dados