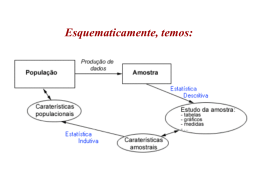
Capítulo 6
• Preparando os dados para data mining
 Os dados são a espinha dorsal do data mining e KDD
 Usualmente os dados não estão disponíveis de uma forma pronta para
data mining;
 O maior desafio para os mineradores é preparar os dados de uma
forma adequada para modelagem;
 Muitos negociadores mantém dados armazenados e facilidades de
acesso – DATA WAREHOUSE;
1
 Data warehousing é definido como um gerenciamento de dados
centralizado e que permite ao analista acessar, atualizar e manter os
dados para análises e relatórios;
 Data warehouse melhora a eficiência em extrair e preparar dados
para data mining;
 Data warehouse populares usam base de dados relacionais
(Oracle, Informix, Sybase), e arquivos com formato de computadores
pessoais (planilhas eletrônicas e MS Access);
 Aproximadamente 70% do tempo de operação de data mining é
gasto com a preparação dos dados obtidos de diferentes fontes; assim
considerável tempo e esforço deveria ser gasto na preparação de
tabelas de dados para estar adequado para modelagem em data
mining.
2
Dados necessários em data mining
Dados resumidos não são adequados para data mining pois
não se tem informação sobre os consumidores ou produtos
individualmente. Por exemplo, para identificar os perfis
dos consumidores, os registros individuais dos
consumidores que incluem as informações são necessários
para criar os cluster baseados em seus padrões de
aquisição. De forma similar, para identificar as
características dos consumidores lucrativos num modelo
preditivo, variáveis target (objetivo, resposta) e de entrada
(preditoras), devem ser incluídas. Assim, para resolver
problemas específicos, dados adequados devem ser
extraídos de data warehouses ou dados novos coletados que
forneçam as exigências do data mining.
3
Estrutura ideal dos dados para data mining
As linhas (que são os casos ou observações) e as colunas (variáveis) similar ao
formato de arquivo de uma planilha eletrônica, é necessário para data mining.
As linhas usualmente contém informações relativos aos consumidores
individualmente ou aos produtos adquiridos.
As colunas descrevem os atributos (variáveis) dos casos individuais.
Informações únicas dos consumidores, como número do telefone, devem ser
excluídas das técnicas de modelagem. Entretanto, estas variáveis com valores
únicos (individuais) podem ser utilizadas como variáveis ID (identificadoras),
para identificar casos individuais e excluir valores discrepantes e extremos.
Também não é recomendável incluir variáveis preditoras contínuas altamente
correlacionadas (coeficiente de correlação maior do que 0,95) nos modelos
preditivos, pois podem produzir modelos instáveis que trabalham com a particular
amostra usada.
4
Colunas com apenas um valor
Não contém informação que possa fazer a distinção entre linhas da base de dados.
Como ela não representa informação dever der desprezada para fins de mineração
de dados.
Coluna com grande predominância de apenas um único
valor
Questão: quando esta(s) coluna(s) podem ser desprezada(s)? 1O ) praticamente
todos os registros devem ter o mesmo valor e 2O) poucos registros com valores
diferentes e que representam uma porção (muito pequena para ter importância)
desprezível dos dados.
5
Coluna com valores únicos
É o outro extremo. São variáveis categóricas que para cada linha assumem um
valor diferente. Exemplos: nome do cliente, endereço, número do telefone, etc.
Estas colunas não tem valor preditivo.
Colunas sinônimos com a variável target
Quando uma coluna é altamente correlacionada com a coluna target isto pode
significar que ela é sinônimo. Exemplo: se um cliente está com o seu cartão de
crédito em inatividade, pode indicar que ele não vai responder a uma campanha de
marketing. Variáveis sinônimos com a variável target devem ser ignoradas da
análise.
6
Entendendo a escala de medida das variáveis
A escala de medida de uma variável de entrada ou de saída determina o tipo de
ferramenta de modelagem que é apropriada para um específico projeto de data
mining.
Como já visto as variáveis podem ser classificadas em dois tipos:
1. Contínuas
2. Categorizadas
As variáveis contínuas (ou intervalares) são variáveis numéricas que
descrevem quantidades e tem uma escala contínua. Média e desvio padrão são
medidas para quantificar uma medida de tendência central e dispersão,
respectivamente. Total de vendas por consumidor, custo por produto, o total de
vendas por produto, o número de unidades adquiridas por cada consumidor, a
renda anual por consumidor, são exemplos de casos intervalares. Uma variável
contínua é necessária para modelagem preditiva em regressão linear múltipla e
redes neurais artificiais.
7
As variáveis categorizadas podem ser classificadas como:
i.
Ordinal
Uma variável com rank (ordenação) categorizada ou discreta com mais de dois
níveis. Exemplo: grupo de idades. Regressão Logística Politômica é adequada para
modelar variáveis ordinais.
ii. Nominal
Uma variável categorizada com mais de dois níveis e não ordenada. A moda é a
estatística mais utilizada para tendência central, e o estudo da distribuição de
freqüência é a técnica mais utilizada para descrição.
Exemplos: diferentes tipos de serviços bancários, raça.
Análise discriminante e Árvores de decisão são métodos adequados para modelar
variáveis objetivo (target) nominais.
iii. Binárias
Uma variável binária com apenas dois níveis. Exemplo: bom e ruim, vendeu e não
vendeu.
Regressão logística é adequada para modelar variável objetivo (target) binária.
8
Números
Métodos de transformação de dados
1) Normalização
Os valores resultantes são dados dentro de uma certa faixa, por exemplo, 0 e 1.
Esta transformação não muda a forma da distribuição dos valores. Normalização
pode ser útil quando usamos técnicas que realizam operações de multiplicação
sobre os dados, tais como Redes Neurais e Cluster Analysis. Árvores de Decisão
não são afetadas pela normalização, pois não muda a ordem dos valores.
Valor  Mín
1,0  0 ,0   0 ,0
v 
Máx  Mín
'
2) Padronização
Transforma os valores em números de desvios padrões a partir da média. É
dada por:
X X
S
z
A padronização não afeta a ordem dos valores.
9
3) Caixas com igual largura (Equal-width binning) [Discretização]
Transforma as variáveis em faixas de tamanhos fixos. A variável resultante tem
aproximadamente a mesma distribuição da variável original. Entretanto, valores
em caixa afetam todos os algoritmos de data mining.
Exemplo: rendimento de domicílios. A distribuição desta variável é bem
assimétrica, devido a outliers. Os valores poderiam ser divididos em 10 faixas, por
exemplo, faixa 1: R$ 0 até R$ 1.500,00.
4) Caixas com igual altura (Equal-height binning) [Discretização]
Transforma as variáveis em decis, percentis, tal que o mesmo número de registros
pertencem a uma mesma caixa. A variável resultante tem distribuição uniforme.
Exemplo: rendimento de domicílios, muito baixo (20% menores rendimentos),
baixo (entre 20% e 40% menores), médio (40% e 60%), alto (60% e 80%) e muito
alto (acima de 80%).
Redes Neurais: valores em caixa é uma forma de reduzir a influência dos outliers,
pois todos os outliers serão agrupados dentro da mesma caixa.
Árvore de Decisão: resulta em folhas que têm tamanhos mais próximos nos níveis
10
mais alto da árvore.
5) Outras transformações
Por exemplo: transformação logarítmica.
Datas e Tempos
Um formato típico para datas e tempo é o número de dias ou horas desde alguma data
no passado. Neste caso os algoritmos tratam datas como números e é adequado para
detectar o que aconteceu mais cedo ou mais tarde.
Variáveis Categorizadas
Os algoritmos trabalham melhor com poucas categorias. Para reduzir o número de
categorias pode-se usar atributos dos códigos, ao invés dos próprios códigos. Pode-se
substituir o CEP pelo rendimento médio ou valor médio da casa, porém tratar como
variável categorizada.
Redes Neurais e Cluster Analysis entendem variáveis quantitativas, portanto, na
presença de variáveis categorizadas, utilizar variáveis binárias.
11
Usar toda a base de dados versus amostra
representativa
Para encontrar tendências e padrões nos dados, mineradores podem usar toda a base
de dados (se desejar uma solução para toda a base) ou selecionar amostras aleatórias
de toda a base. Com os recursos computacionais atuais é possível analisar toda a
base de dados, porém, o uso de amostras representativas selecionadas aleatoriamente
na construção de modelos é mais atrativo pelas seguintes razões:
 Usando amostras aleatórias permite ao analista desenvolver o modelo a partir de
amostra de treinamento1 ou calibração, validar o modelo2 com um arquivo de “
validação”, e testar3 o modelo com outra amostra teste independente.
 Minerar uma amostra aleatória representativa é mais fácil e mais eficiente e pode
produzir resultados precisos similares àqueles produzidos usando toda a base de
dados.
 Quando amostras são usadas, a exploração e visualização dos dados ajudam a
ganhar conhecimento, que por sua vez, conduzem aos modelos mais rapidamente e
com maior precisão.
 Amostras representativas necessitam relativamente de menor tempo para limpeza,
12
exploração, e desenvolver e validar modelos. Isto implica em menor custo.
1
Usado para ajuste inicial do modelo. Por exemplo, usada para
estimar os parâmetros do modelo de regressão, ou seja, gerar
uma explicação da variável dependente em termos das variáveis
independentes.
2A validação
de modelos obtidos a partir de arquivo de dados de
treinamento através de arquivos de validação independentes é
uma importante exigência em data mining para confirmar a
usabilidade do modelo criado. A validação do modelo verifica a
qualidade do modelo ajustado e protege contra a
superparametrização ou sub-parametrização do modelo. Assim,
a validação do modelo pode ser considerada a etapa mais
importante na seqüência da construção do modelo. É o ajuste
fino, usada para selecionar o melhor modelo. Para isso existem
critérios de seleção de modelos.
3
É a avaliação do modelo.É usada para testar a performance do
modelo selecionado. Dados ainda não utilizados pelo modelo
13
Amostragem para data mining
A amostra usada na modelagem deve representar toda a base de dados porque o
objetivo principal em data mining é fazer predições sobre toda a base de dados.
O tamanho e outras características da amostra selecionada determina se a amostra
usada na modelagem é representativa de toda a base de dados.
Os seguintes tipos de amostragem são comumente usados em data mining:
I.
Amostragem Aleatória Simples
II.
Amostragem de Conglomerados
III.
Amostragem Aleatória Estratificada
14
I.
Amostra aleatória simples
É o plano de amostragem mais comumente utilizado em data mining.
Cada observação, registro ou caso da base de dados tem igual chance de
ser incluída na amostra.
A amostra aleatória simples serve quando a população é razoavelmente
homogênea para a característica em estudo.
Exemplo: clientes de cartão de crédito especial (internacional) de um
determinado banco.
15
Uso do SAS para obtenção de uma amostra aleatória simples.
Nome do arquivo de dados: wilson.txt
Nome do programa SAS: Amostra_aleatoria_simples.sas
Estimação
Objetivo: obter estimativas para valores populacionais desconhecidos, tais como
a média ou a proporção.
16
Variáveis quantitativas
A estimativa da média populacional é feita através da média da amostra selecionada,
calculada por:
n
x
x
i 1
i
n
A variância populacional, 2X, é estimada através da variância da amostra:
n
s X2 
2


x

x
 i
i 1
n 1
17
A variância da média amostral será calculada, na amostra sorteada por:
2
s
s x2  1 f  X
n
Onde f=n/N é a fração de amostragem.
Exemplo: deseja-se estimar a concentração média de fumonisina (micotoxina no
milho armazenado), dada em ug/g, no Estado de Santa Catarina. Através de uma
amostra casual simples de 10 armazéns, os resultados obtidos foram:
1,05
3,25
0,78
2,21
4,01
1,98
0,68
2,28
2,02
1,15
18
Os resultados obtidos foram:
x  1,941g / g
s X2  1,1719(g/g) 2
sx2  1,1719/ 10  0,1172
Pois f=n/N  0 (zero)
sx  0,3426g/g
Variáveis qualitativas
Exemplo: Foi realizada uma pesquisa por amostragem em 4 estabelecimentos
comerciais no município de Florianópolis sobre o consumo de tomates
minimamente processados. Duas variáveis qualitativas de interesse foram:
1.
O consumidor prefere tomates com casca de cor: a) verde; b) rosado ou c)
vermelho;
2.
Se o consumidor compraria o tomate fatiado e embalado.
19
No caso da variável 2, deseja-se estimar a porcentagem (), de consumidores
que comprariam o tomate fatiado e embalado.
Em casos dicotômicos, pode-se definir uma nova variável quantitativa da
seguinte forma:
x=1 se compraria
x=0 se não compraria
Assim, a proporção de casos favoráveis na amostra, p, pode ser tratada como:
xp
A variância de P é calculada por:
 pq 
s  1  f 

 n 1 
2
P
Onde q=(1-p).
20
Exemplo: Os resultados obtidos na pesquisa (n=400 consumidores) foram:
Consumo
ni=freqüência absoluta
Consumiria
364
Não Consumiria
36
Total
400
364
px
 0,91  91%
400
pq 0,91(0,09) 0,0819
s 


 0,00021
n 1
400  1
399
2
P
Pois 1-f é desprezível.
sP  0,0143 1,43%
21
No caso da variável 1, cor da casca, com 3 categorias (politômica), a variância da
proporção é calculada como anteriormente:
s
2
P



 1 f 
pq 

 n 1 
fixando-se a categoria de interesse e reunindo todos os demais elementos
(pertencentes às outras categorias) na classe que corresponde ao valor 0 (zero)
para X.
Exemplo: para estimar a proporção de consumidores que preferem tomates
com casca vermelha, tem-se:
p
244
 0,61
400
q=1-0,61=0,39.
Assim:
0,61(0,80)
s 
 0,00122
400  1
2
P
sP  0,035 3,5%
22
Intervalos de confiança
Deseja-se, a partir das estimativas pontuais, construir expressões que com certo
coeficiente de confiança, nos forneçam informações sobre os valores
populacionais desconhecidos. Ou seja, desejamos construir um intervalo dentro do
qual esperamos que esteja o verdadeiro valor da característica em estudo.
Exemplo: vamos construir o intervalo de confiança para a concentração média de
fumonisina (vamos supor que a amostra seja grande).
x  1,941
s x  0,3423
2,00* s x  2,00* 0,3423 0,6846
x  2,00* s x  1,941 0,6846 1,2564
x  2,00* s x  1,941 0,6846 2,6256
 1,2564   2,6256
23
Exemplo: vamos construir o intervalo de confiança para a proporção dos
consumidores que preferem tomates com casca de cor vermelha.
p  0,61
sP  0,035
2,00* sP  2,00* 0,035  0,07
p  2,00* s P  0,61 0,07  0,54
p  2,00* sP  0,61 0,07  0,68

0,54    0,68
24
II.
Amostra estratificada
A base de dados é dividida em estratos mutuamente exclusivos (intersecção
é nula) ou sub-populações; amostras aleatórias são retiradas de cada estrato,
podendo ser, por exemplo, proporcional aos seus tamanhos.
Situação de uso: quando a população apresenta grande variabilidade com
respeito a variável em estudo. Nesse caso, procede-se a divisão da
população de N elementos, em sub-populações, sem superposição
(ESTRATOS) de tamanho nh. Estes estratos devem ser internamente mais
homogêneos que a população toda.
O critério para a formação dos estratos deve ter relação com a(s) variável(is)
em estudo (target, objetivo) e, que derive estratos homogêneos.
25
Fatores que contribuem para a não utilização de uma AAS:
a)
A população é extremamente heterogênea, o que acarreta falta de precisão
nas estimativas. Exemplo: levantamento da renda familiar no município de
Florianópolis.
b)
A população se subdivide naturalmente em diferentes setores, áreas de
estudo, ou regiões geográficas. Neste caso há interesse em enfocar cada
parte isoladamente. Exemplo: levantamento de dados para as estimativas e
previsões de produção de leite no Estado de Santa Catarina, podemos ter:
Região Litorânea, Baixo, Médio e Alto Vale do Itajaí, Planalto e Oeste
Catarinense.
c)
Embora a população seja homogênea e não se subdivida naturalmente em
setores ou áreas, a própria natureza do problema nos indica a necessidade
de se enfocar isoladamente certos campos. Interesse em produzir
estimativas para os estratos. Nesse caso, a precisão é fixada para cada
estrato que passa a se chamar domínio. Exemplo: podemos estar
interessados em estudar isoladamente cada grande rede de supermercados
de Florianópolis.
26
d)
Sistemas de referências diferentes, isso implica na aplicação de planos e/ou
estimativas diferentes em cada estrato.
e)
Deseja-se controlar o efeito de alguma característica na distribuição da
característica que está sendo avaliada. Exemplo: o efeito da escolaridade dos
chefes de famílias sobre o estado nutricional de crianças menores de 5 anos
pode ser controlado pela composição de uma amostra que contenha os
diversos níveis de escolaridade dos chefes de família da população estudada.
Outro exemplo: num estudo da avaliação do desvio da torção permanente do
tronco (coluna vertebral) pode-se estratificar por sexo, categorização por
grau de dor, categorização por grupos de idades.
f)
Deseja-se que a amostra mantenha a composição da população segundo
algumas características básicas. Por exemplo, em estudos sociais ou
epidemiológicos, é usual a obtenção de amostras que apresentam
composição segundo o sexo e a idade semelhante à população estudada.
g)
Deseja-se obter amostras viesadas para fins de modelagem. Por exemplo:
em estudos de marketing, é usual a obtenção de amostras que apresentam
praticamente a mesma porcentagem de respondentes e não respondentes.
27
Exemplos:
1.
Estratificação pela qualificação dos operários.
2.
Estratificação dos supermercados da grande Florianópolis de acordo com o
número de caixas.
3.
Estratificação de uma cidade em bairros
4.
Estratificação de uma população por sexo, por nível de escolaridade, tamanho
da cidade, idade.
5.
Estratificação das empresas por volume de vendas ou por setores.
6.
Estratificação das propriedade agrícolas pelo número de vacas leiterias.
28
Exemplo
Objetivo: fazer um levantamento para estimar a proporção de aceitação de
uma nova formulação de alimento em uma população de escolares de
primeiro grau.
A aceitação do novo alimento é diferente quando se considera a idade e o
sexo das crianças, é recomendável que essa população seja estratificada
por essas características, antes da seleção da amostra.
29
Obtenção da amostra
População
Amostra
Estrato 1
Estrato 1 da amostra
Estrato 2
•
Estrato 2 da amostra
Amostra
•
Estratificada
•
•
Estrato k
Estrato k da amostra
30
Notação
N representa o tamanho da população;
Nh é o tamanho do h-ésimo estrato da população;
Nh
é o peso do estrato h (ponderação).
Wh 
N
31
Cálculo da média estratificada
k
xest   Wh xh 
h 1
onde k é o número de estratos, e
nh
xh 
x
i ,h
i 1
nh
A variância da média estratificada é dada por:

k
s
2
xest
W s
h 1
2 2
h x ,h
s
 x
nh
onde
2
x ,h

2
h
s
 1  f h 
nh
nh
fh 
Nh
sh2 
i 1
i ,h
 xh 
nh  1
2
32
Amostra estratificada Uniforme
Sorteia-se igual número de elementos em cada estrato.
n
nh 
k
Uso
1.
Quando o interesse é derivar estimativas para cada estrato, ou quando desejase comparar diversos estratos.
2.
É recomendável quando os estratos da população forem aproximadamente do
mesmo tamanho.
33
Exemplo: selecionar uma amostra estratificada uniforme de tamanho n=12 da
comunidade da universidade. Nesse caso devemos selecionar quatro pessoas de
cada categoria (Professores, Estudantes e Técnicos Administrativos).
N=12
k=3
nh=12/3=4, portanto, n1=n2=n3=4
Objetivo: deseja-se estimar o número médio de pessoas por família.
Amostra 1 (Professores): 2 3 3 4
Amostra 2 (Estudantes): 4 5 6 6
Amostra 3 (Técnicos-Administrativos): 4 6 7 7
34
Cálculo da média amostral
h
nh
X 
xh
1
2
3
4
4
4
(2,3,3,4)
(4,5,6,6)
(4,6,7,7)
3,00
5,25
6,00
i ,h
Nh
Wh 
N
2500/22500=0,11
15000/22500=0,67
5000/22500=0,22
3
xest   Wh xh   0,11* 3  0,67* 5,25  0,22* 6,00  5,1675
h 1
35
Cálculo da variância amostral
h
nh
1
2
3
4
4
4
4/2500=0,0016
4/15000=0,0003
4/5000=0,0008
3
s

s h2
n
fh  h
Nh
2
xest

0,67
0,92
2,00
W s
 
h 1
s X2 ,h
2 2
h X ,h
(1-0,0016)0,67/4=0,1672
(1-0,0003)0,92/4=0,2299
(1-0,0008)2,00/4=0,4996

 

sx2est  0,112 * 0,1672  0,672 * 5,25  0,222 * 6,00  5,1675
sxest  0,1294  0,3597pessoas/família
O desvio dos valores em
relação à média é, em
média, igual a 0,3597. 36
Intervalo de confiança
x  2,00* sxest  5,1675 2,00* 0,3597 5,1675 0,7194
4,45    5,88
Pode-se afirmar com 95% de confiança que a média real está entre 4,45 e 5,88.
37
Amostra Estratificada Proporcional
População
Amostra
Professores
20%
Professores
20%
Servidores
20%
Servidores
20%
Alunos
60%
Alunos
60%
A proporção na população é mantida na amostra. A amostra sorteada será ,
portanto, considerada auto ponderada, e o procedimento de estimação poderá
sofrer simplificações. Melhor quando as variâncias dos estratos são próximas.
38
Exemplo
Objetivo: levantar o estilo de liderança preferido
População: 10 professores, 10 servidores e 30 alunos
Amostra: amostragem estratificada, proporcional por categoria, de tamanho
n=10. (podemos determinar o valor de n; para isso precisamos da variância,
precisão e confiança).
Cálculo do tamanho da amostra por estrato
Estrato
Professores
Servidores
Alunos
Proporção na
população
10/50=0,20=20%
10/50=0,20=20%
30/50=0,60=60%
Tamanho do estrato
na amostra
np=20% de 10=2
ss=20% de 10=2
na=60% de 10=6
Fator de amostragem
f1=2/10=0,20=20%
F2=2/10=0,20=20%
f3=6/30=0,20=20%
39
Estrato são mais homogêneos que a população, isto implica em resultados mais
precisos (mais próximos dos parâmetros~), e necessidade de menor tamanho de
amostra.
Uso do SAS para obtenção de uma amostra aleatória
estratificada.
Nome do arquivo de dados: wilson.txt
Nome do programa SAS: Amostra_estratificada_uniforme_proporcional.sas
40
Exemplo
Objetivo: estimar o número médio de pessoas por família.
População: 10 professores, 10 servidores e 30 alunos.
Amostra: n=10 (2 professores(20%), 2 servidores (20%) e 6 alunos (60%))
n1=0,20*10=2 (20% da amostra)
n2=0,20*10=2 (20% da amostra)
n3=0,60*10=6 (60% da amostra)
A média estratificada e a variância, simplificam-se para:
n
xest   xi / n  x
i 1
s
2
xest

1 f 

n
k
W s
h 1
2
h h
41
Cálculo da média e da variância da média amostral
h
1
2
3
nh
2
2
6
(xi,h)
(3, 4)
(4, 8)
(5, 6, 4,
8, 6, 7)
s h2
0,50
8,00
2,00
Wh=Nh/N
10/50=0,20
10/50=0,20
30/50=0,60
Wh s h2
0,10
1,60
1,20
x  5,5 pessoas/família
s
2
xest
 1  0,20 

* 2,90  0,232

 10 
s xest  0,232  0,4817 pessoas/família
42
Intervalo de confiança
5,5  2,00* 0,4817
5,5  0,9634
4,5    6,5
43
Estimativas para proporções
Partilha proporcional
Exemplo
Objetivo: estimar a proporção de crianças vacinadas.
População: 984 crianças menores de 12 meses.
Estrato 1: crianças com assistência pré-natal, N1=325.
Estrato 2: crianças sem assistência pré-natal, N2=659.
Amostra: f1=f2=f=200/984=0,2033
n1=66
n2=134
Resultados: no estrato 1, 33 foram vacinadas e, no estrato 2, 40 crianças foram vacinadas.
44
200
pest  x   xi / 200  73/ 200  0,365(36,5%)
i 1
Cálculo da variância:
h
1
2
Wh
325/984=0,3303
659/984=0,6697
nh
66
134
ph
0,50
0,30
qh
0,50
0,70
Wh(ph)(1-ph)(nh/(nh-1))
0,0838
0,1417
k


nh 
1

f


2
 
s pest  
 Wh ( ph )(1  ph )
nh  1 
 n  h 1
1  0,2033
2
0,0838 0,1417  0,000898
s pest 
200
 s pest  0,000898 0,0299 0,03(3%)
45
Intervalo de confiança:
IC ;95%  : pest  1,96* s p
est
IC ;95%  : 0,365 1,96* 0,0299
IC ;95%  : 0,365 0,0586
 0,3064   0,4236
46
iii. Amostragem de Conglomerados
A base de dados é dividida em clusters (grupos) no primeiro estágio da seleção
da amostra e alguns desses clusters são aleatoriamente selecionados através de
uma amostragem aleatória . Todos os registros dos clusters aleatoriamente
selecionados são incluídos no estudo.
Cada conglomerado é uma mini-população  os conglomerados são subgrupos
heterogêneos.
É adequada quando é possível dividir a população em um grande número de
sub-populações.
Vantagens:
 Facilidade administrativa.
 Tende a ser mais econômica.
Não exige uma lista de todos os elementos da população. Basta uma lista dos
conglomerados selecionados.
47
Desvantagens:
 Produz uma amostra que gera resultados menos precisos do que uma AAS ou
AE.
48
População dividida em conglomerados
Primeiro estágio: seleção aleatória de conglomerados
Segundo estágio: seleção aleatória de elementos
Amostra
49
Exemplo:
1.
Numa população de domicílios de uma cidade, os quarteirões formam
conglomerados de domicílios.
2.
Numa população de propriedades agrícolas no Estado de Santa Catarina,
os municípios formam conglomerados.
3.
Numa população de domicílios do Estado de Santa Catarina, podemos no
primeiro estágio, selecionar municípios, no segundo estágio, selecionar
quarteirões e, finalmente, no terceiro estágio selecionar domicílios.
50
Exemplo:
Deseja-se sortear uma amostra de 500 escolares (elementos). Vamos sortear
algumas escolas e considerar todas as crianças dessas escolas para compor a
amostra. Se as escolas tivessem o mesmo número de crianças (Bj=100), o
procedimento seria por conglomerados em um único estágio, e (n=a*Bj) ou
(500=5*100).
Outros procedimentos (3 estágios)
50 escolas  2 classes por escola  5 crianças por classe
25 escolas  4 classes por escola  5 crianças por classe
51
Exemplo
Pesquisa Nacional por Amostra de Domicílios (PNAD) (Fundação IBGE).
Primeiro estágio:amostras de municípios para cada uma das sete regiões
geográficas do Brasil.
Segundo estágio: setores censitários (áreas menores, por exemplo, 300
domicílios) são sorteados em cada município.
Terceiro estágio: sorteados domicílios.
52
Como selecionar a amostra?
Primeiro estágio: selecionar conglomerados de elementos.
Segundo estágio: 1) observa-se todos os elementos dos conglomerados
(amostragem em um estágio único);
2) faz-se a seleção de elementos dos conglomerados (AAS,
AE, AC).
53
Exemplo
Selecionar uma amostra de domicílios de uma cidade de tamanho n=12, em 3
conglomerados (ruas). Pode-se tomar as ruas como conglomerados.
Ruas
A
B
C
D
E
Domicílios
A1
B1
C1
D1
E1
A2
B2
C2
D2
E2
A3
B3
C3
D3
E3
A4
B4
C4
D4
E4
A5 A6
B5 B6 B7 B8 B9 B10 B11 B12 B13 B14
C5 C6 C7 C8 C9 C10
E5 E6 E7
Primeiro estágio: sorteio de conglomerados (ruas).
Segundo estágio: sorteio de domicílios, dentro de cada rua selecionada
54
Amostragem de Conglomerados em Um
Único Estágio- Conglomerados de
Tamanhos Diferentes
Notação:
População:
1
2
...
i
...
M
XiT é o total do cluster;
Ni é o tamanho do cluster i;
Ni
X iT   X ij
j 1
X i é a média do luster
c
Xij valor da variável de interesse do elemento j
e cluster i.
55
Amostra: a amostra de cluster consiste de todos os elementos de cada um dos m
cluster selecionados aleatoriamente a partir dos M cluster da população.
1
2
...
i
...
m
xiT é o total do cluster;
ni é o tamanho do cluster;
xi é a média do luster
c
Unidades primárias: são os clusters;
Unidades secundárias: são os elementos da população dentro dos clusters;
A amostra de cluster é uma amostra aleatória simples de clusters.
56
A média populacional geral (isto é, o valor médio de X das unidades secundárias) é:
M
Ni
M
X   X ij
M
M
N  X N
i 1 j 1
i 1
i
i 1
iT
i 1
i
Interpretação: razão do total dos valores XiT para o total dos valores Ni.
Estimação: desejamos estimar X(barra) a partir de uma
amostra de conglomerados.
m
xC   xiT
i 1
m
n
i 1
i
A qual é a razão da soma dos totais de clusters para a soma dos tamanhos de clusters,
na amostra de clusters selecionada.
57
Variância de
xC
pode ser estimada a partir da amostra por:
2

M  mM m  ni 
2


VarxC  
x

x
  i C

mm  1 i 1  N 
E se N for desconhecido, ele pode ser substituído pelo estimador Mn/m, onde n é o
tamanho efetivo da amostra, obtendo-se:
VarxC  
M  mm  ni  x  x 2
  i C

M m  1 i 1  n 
m
2
Estimação do total geral XT
xT  NxC
Var  xT   N 2Var  xC 
58
Exemplo:
Trata-se de avaliar o rendimento dos alunos da primeira série do primeiro grau,
na rede de ensino público de certa localidade.
A partir da relação das 3500 turmas existentes, foram preparados
conglomerados (clusters), juntando turmas de diferentes escolas, com o objetivo
de grupar alunos o mais possível diferentes no que se refere ao rendimento
(necessidade dos conglomerados serem heterogêneos).
Os conglomerados foram formados com 5 turmas e, aproximadamente, 150
alunos, supondo uma base de 30 alunos por turma.
Deseja-se observar uma amostra de 1500 alunos.
Considerando:
n  mN  m  1500/ 150  10 conglomera
dos
59
Conglomerados da
amostra
1
2
3
4
5
6
7
8
9
10
Total
Número de alunos
ni
162
170
145
151
160
162
145
148
171
178
1592
Soma dos escores
xiT
1004,4
952,0
1015,0
830,5
960,0
793,8
855,5
947,2
1214,1
1032,4
9604,9
60
Estimativa do rendimento médio por aluno
m
m
xC   xiT
n
i 1
10
xC   xiT
i 1
10
n
i 1
i
i
i 1
 9604,9 / 1592 6,033
Estimativa da variância de xC

M  mm  ni 
2
VarxC  
  xi  xC 

M m  1 i 1  n 
m
2
61
Conglomerados
ni
n
1
2
3
4
5
6
7
8
9
10
Total
0,1018
0,1068
0,0911
0,0948
0,1005
0,1018
0,0911
0,0930
0,1074
0,1118
 ni 
 
n
2
0,0104
0,0114
0,0083
0,0090
0,0101
0,0104
0,0083
0,0086
0,0115
0,0125
xi  xC 
 x i  x C 2
0,1670
-0,4330
0,9670
-0,5330
-0,0330
-1,1330
-0,1330
0,3670
1,0670
-0,2330
0,0279
0,1875
0,9351
0,2841
0,0011
1,2837
0,0177
0,1347
1,1385
0,0543
 ni 
 
n
2
 x i  x C 2
0,00029
0,002138
0,007761
0,002557
1,11E-05
0,01335
0,000147
0,001158
0,013093
0,000679
0,041184

700 1010
Var xC  
0,041184 0,451
70010  1
62
Estimativa do coeficiente de variação de
xC
Var( xC )
0,451
CV xC  

 0,1113
xC
6,033
Estimação de uma Proporção
Notação:
X é uma variável de interesse de estudo. Por exemplo: 1) número de famílias
com casa própria; 2) número de domicílios com pelo menos um automóvel.
Xij = 1 se o elemento j do conglomerado i tem o atributo ou característica em estudo;
Xij = 0 se o elemento j do conglomerado i não tem o atributo ou característica em
estudo;
63
População:
XiT é a quantidade de elementos que possui o atributo ou a característica em
estudo no conglomerado i.
Ni
X iT   X ij
j 1
X iT
Xi 
 Pi
Ni
A proporção de elementos que possuem o
atributo ou a característica no conglomerado i
M
X 
X
i 1
M
iT
N
i 1
i
P
A proporção dos elementos que
possuem o atributo ou a característica
na população
64
Estimador:
m
Proporção na
população
pC 
x
i 1
m
iT
n
i 1
i
xiT é a quantidade de elementos que possuem o atributo no conglomerado i
selecionado.
ni é o tamanho (a quantidade de registros, casos, observações) no conglomerado i
selecionado.
65

M  mm  ni 
2


Var pC  
p

p
  i

C
M m  1 i 1  n 
m
2
n é a quantidade total de registros, casos ou observações na amostra
selecionada.
pi é a proporção amostral de elementos com o atributo no conglomerado i
selecionado.
66
Exemplo:
No exemplo anterior observou-se, também, o número de alunos fumantes, cujos
resultados foram:
Conglomerados da
amostra
Número de alunos
(ni)
1
2
3
4
5
6
7
8
9
10
Total
162
170
145
151
160
162
145
148
171
178
1592
Número de alunos que
fumam
(xiT)
50
63
47
48
68
59
36
45
71
75
562
67
 Estimativa da proporção dos alunos que fumam
m
pC 
x
i 1
m
iT
n
i 1
562

 0,3530 35,3%
1592
i
 Estimativa da variância da proporção dos alunos que
fumam

M  mm  ni 
2


Var pC  
p

p
  i

C
M m  1 i 1  n 
m
2
68
Conglomerados ni
da amostra
1
2
3
4
5
6
7
8
9
10
Total
162
170
145
151
160
162
145
148
171
178
x iT
50
63
47
48
68
59
36
45
71
75
ni
n
0,101759
0,106784
0,09108
0,094849
0,100503
0,101759
0,09108
0,092965
0,107412
0,111809
 ni 
 
n
2
0,010355
0,011403
0,008296
0,008996
0,010101
0,010355
0,008296
0,008642
0,011537
0,012501
pi
0,308642
0,370588
0,324138
0,317881
0,425
0,364198
0,248276
0,304054
0,415205
0,421348
 p i  p C 2
0,001969
0,000309
0,000834
0,001234
0,005182
0,000125
0,01097
0,002397
0,003868
0,004669
2
 ni 
2
   pi  pC 
n
2,03884E-05
3,52137E-06
6,91765E-06
1,11053E-05
5,23404E-05
1,29485E-06
9,10057E-05
2,07175E-05
4,46212E-05
5,83738E-05
0,000310286

700 1010
Var pC  
0,000310286 0,0003398
70010  1
DP pC   0,000310286 0,017615
69
Determinação do Tamanho de uma Amostra
Aleatória Simples
Para a determinação do tamanho da amostra é preciso fixar o erro máximo
desejado, o grau de confiança do intervalo de confiança e ter algum
conhecimento a priori da variabilidade da população. Os dois primeiros são
fixados (fornecidos) pelo responsável pelo trabalho, enquanto o terceiro pode
ser obtido de pesquisas passadas (referências bibliográficas), próprios dados
do pesquisador ou de amostras pilotos. Outro procedimento é considerar um
intervalo onde aproximadamente 95% dos indivíduos da população estariam
concentrados, e aí, igualar à amplitude deste intervalo a quantidade 4 (pois,
se os dados seguem aproximadamente uma distribuição normal, então, 95%
dos mesmos encontram-se no intervalo média2*desvio padrão). Podemos,
grosseiramente estimar s tomando-se os 2 valores extremos dos dados e
determinar a amplitude.
O tamanho da amostra depende também da estatística que se deseja estudar
(média, proporção ou um total), se a amostra é com ou sem reposição e dos
custos.
70
Conceito de erro amostral
Chama-se de erro amostral a diferença entre o valor que a estatística
pode acusar e o verdadeiro valor do parâmetro que se deseja estimar.

e  ˆ 

Aumentando-se o tamanho da amostra, as estimativas amostrais
aproximam-se cada vez mais dos valores populacionais (o erro amostral
diminui)
71
Amostragem para proporções
Se deseja-se estimar uma proporção na população e queremos, com nível (1-)
de confiança, que a proporção da amostra esteja, no máximo a uma distância e
da proporção verdadeira, então:
n  z P1  P / e
2
2
Onde:  é o risco aceitável de que a proporção populacional esteja fora dos
limites pe; z é o valor que elimina a área  de ambos os lados (bilateral)
da distribuição normal (valores obtidos em tabelas ou softwares da
distribuição normal); P é a proporção populacional.
A proporção populacional geralmente não é conhecida, então usa-se alguma
estimativa para a mesma; pode ser de um estudo anterior, referências
bibliográficas, pode-se também usar p=1/2, assim,
n  z 4e
2
2
Neste caso, a amostra será, possivelmente, superestimada.
72
Para valores de P muito pequenos (P < 0,10), a aproximação de Poisson
pode ser utilizada, e o cálculo do tamanho da amostra é dado por:
n  z P / e
2
2
Quando a amostragem é sem reposição, e a fração de amostragem n/N não é
desprezível (n  0,05N), uma estimativa mais satisfatória do tamanho da
amostra é dada por:
n 
'
n
n
1
N
(1)
Onde n é obtido como na equação dada anteriormente.
73
Exemplo:
Deve-se realizar uma pesquisa sobre consumo de hortaliças. Deseja-se
determinar a proporção de pessoas que consomem tomate no preparo da salada.
Quantas pessoas deverão ser ouvidas para que sejam satisfeitas as seguintes
condições: e(precisão da pesquisa)=0,05; p=0,60; (1-)( confiança dos
resultados)=0,95, isto implica que z=1,96. O tamanho da amostra será:
(3,84)(0,60)(0,40)
n
 368 pessoas
2
0,05
Para p=1/2, teríamos:
z2
3,84
n 2 
 384 pessoas
2
4e
4(0,05)
74
Amostragem para médias
O tamanho da amostra, n, é calculado por:
 t * s 
n

 e 
2
Onde s é o desvio padrão e t é um valor obtido na tabela ou software da
distribuição t de Student; este valor depende do nível de confiança (1-) e do
tamanho da amostra.
Quando a amostragem é sem reposição e a fração de amostragem é maior ou
igual a 5%, usar a expressão (1) para correção para população finita.
75
Exemplo:
Deseja-se realizar um estudo sobre o fornecimento de leite, em litros, em uma
cooperativa que reúne 180 pequenos produtores, no mês de dezembro.
Dimensionar uma amostra, com grau de precisão e=0,10(média da amostra
piloto), com a finalidade de se estimar a média, com grau de confiança de 95%.
Utilizar uma amostra piloto de tamanho n=12.
150
285
Temos:
400
300
Tabela: Amostra piloto
320
140
310
230
300
500
285
474
t( 0, 05;11)  2,201
n
s2 
2


y

y
 i
i 1
 12.135,42
n 1
e  0,10(307,8
)  30,78 litros
s  s 2  110,16 litros
76
Portanto:

2,201 12.135,42
n
 61,99  62
2
30,782
A fração de amostragem n/N=62/180=0,3444, é maior do que 5%, e a
amostragem foi feita sem reposição, então o tamanho final da amostra será:
62
n 
 46,11  47.
62
1
180
'
Então devemos acrescentar mais 35 fornecedores na amostra piloto.
77
Referências Bibliográficas
Barbetta,P.A.(1998), Estatística Aplicada às Ciências Sociais, Florianópolis:
Editora da UFSC.
Bolfarine,H.,e Bussab,W.O.(1994), Elementos de Amostragem, 11º Simpósio
Nacional de Probabilidade e Estatística, Belo Horizonte, MG.
Cochran,W.G.(1977), Sampling Techniques, New York: John Wiley & Sons.
Silva, N.N.(1998), Amostragem Probabilística, São Paulo: Editora da
Universidade de São Paulo.
Som,R.K.(1996), Practical Sampling Techniques, New York: Marcel Dekker,
Inc.
78
Software para amostragem:
SAMPLING
Endereço: www.est.ufmg.br/sampling/
(Funciona acoplado ao MINITAB)
Professora coordenadora: Sueli Ap. Mingoti.
79