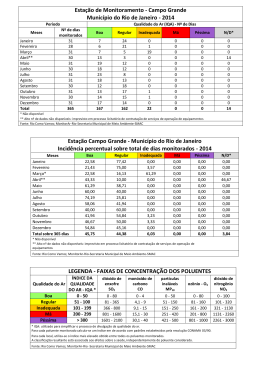
A variação de temperatura da atmosfera com a
altitude, é dada pela constante l
dT
 l
dz
Para atmosfera padrão o valor de l é de 6,5 oK/km, para
z  11km, To = 288,15 oK e po = 101,323 kPa. Onde To e
po são a temperatura e pressão em z = 0.
A variação adiabática de temperatura da atmosfera
com a altitude, é dada pela constante G
1  g
G
 9,8K/km
 R
Onde  é a razão de calor específico, R é a constante do
gás (Ar) e g a aceleração da gravidade.
Dessa forma:
l < G é a condição de equilíbrio estável;
l = G é a condição neutra;
l > G é a condição estatisticamente instável.
A freqüência natural (Brunt-Väisällä) de oscilação de um
poluente sob empuxo (devido a diferença de
temperatura), o qual atingiu a altura de equilíbrio,
depende das propriedades do ar atmosférico e é dada
por:
g
N
(G  l )
T
, Gl > 0
O fluxo de calor da chaminé é dado por:
Q  Cpc (Tc  Ta )  c wc
Onde:
Cpc
Tc
Ta
rc
wc
dc
d c2
4
é o calor específico do poluente
é a temperatura do poluente
é a temperatura do ar
é a massa específica do poluente
é a velocidade de saída do poluente
é o diâmetro da chaminé
O fluxo de empuxo é definido por:
g (Tc  Ta )c wc d c2
Fb 
Ta
4
O comprimento de empuxo é definido por:
gQ
lb 
CpTau 3
Se o produto Cp for o mesmo para o gás poluente e
para a atmosfera, a expressão do comprimento de
empuxo é dada por:
Fb
lb  3
u
O parâmetro de estabilidade é definido por:
u
S
lb N
A sobre-elevação da pluma é dada por:
h  2.27lb S 2 / 3
E calcula-se a altura efetiva através da expressão simples:
H  h  Hc
Onde Hc é a altura da chaminé
Finalmente, a concentração em (x,y,z) pode ser
determinada usando a equação:
 y 2 
 ( z  H )2 
 ( z  H )2 


exp
c ( x, y , z ) 
exp 

exp




2
2
 2 2 
2u  y z
2

2

y 
z
z






Qp
Para z = 0, a equação se reduz a:
2 
 y2
H

c ( x, y , z ) 
exp 

2
2
 2

u  y z
2

y
z


Qp
Onde Qp é a vazão de poluente em [g/s]
Os coeficientes de dispersão y e z são determinados a partir
da tabela e figuras a seguir (levando em conta as classes
atmosféricas):