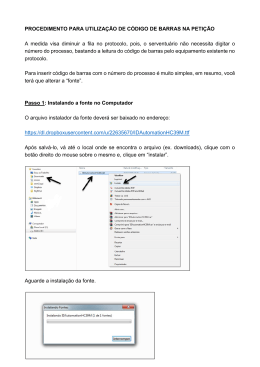
Universidade Federal da Bahia
Escola Politécnica
Departamento de Engenharia Elétrica
Programa de Pós-Graduação em Engenharia
Elétrica
Reconfiguração Ótima de Sistemas de
Distribuição de Energia Elétrica
Aplicando o Algoritmo
MAX-MIN Ant System
Autor:
Orientador:
Huilman Sanca Sanca
Prof. Dr. Niraldo Roberto Ferreira - UFBA
Dissertação submetida à Coordenação do Programa de
Pós-Graduação em Engenharia Elétrica da Universidade
Federal da Bahia, como parte dos requisitos para obtenção
do Tı́tulo de
Mestre em Engenharia Elétrica
Linha de Pesquisa: Sistemas de Potência
Área de Concentração: Processamento de Energia
Banca Examinadora
Dr. Niraldo Roberto Ferreira - UFBA (Presidente)
Dr. André Luı́s de Carvalho Valente - UFBA Dr. Renato José Pino de Araújo - UNIJORGE
Dr. Benemar Alencar de Souza - UFCG
Salvador-BA-Brasil, 26 de Julho de 2013.
i
c
Copyright 2013
de Huilman Sanca Sanca. Texto editado em LATEX2e
FICHA CATALOGRÁFICA
S199
Sanca, Huilman Sanca
Reconfiguração ótima de sistemas de distribuição de energia
elétrica aplicando o algoritmo MAX-MIN Ant System /
Huilman Sanca Sanca. - Salvador, 2013.
110 f. : il. color.
Orientador: Prof. Dr. Niraldo Roberto Ferreira.
Dissertação (mestrado) - Universidade Federal da Bahia.
Escola Politécnica, 2013.
1. Energia elétrica - Distribuição. 2. Algoritmos. 3. Análise
combinatória. I. Ferreira, Niraldo Roberto. II. Universidade
Federal da Bahia. III. Tı́tulo.
CDD: 621.31
ii
Com muito amor dedico este trabalho a Deus e a minha familia. Por tudo que o eles
representam para mim e pelo apoio que me deram em toda a minha vida para a
realização de meus objetivos, especialmente a meu pai e a minha mãe.
Juan e Victoria Melina
iv
”Se eu fui capaz de ver mais longe é porque estava de pé nos ombros de gigantes”
Isaac Newton (1643 - 1727)
v
vi
Resumo
Dissertação de Mestrado
Programa de Pós Graduação em Engenharia Elétrica
Universidade Federal da Bahia
Reconfiguração Ótima de Sistemas de Distribuição de Energia Elétrica
Aplicando o Algoritmo MAX-MIN Ant System
Autor: Huilman Sanca Sanca
Orientador: Niraldo Roberto Ferreira
Neste trabalho apresenta-se uma metodologia para resolver o problema da reconfiguração de sistemas de distribuição de energia elétrica. Este caso pode ser visto
como um problema de programação não linear de variáveis inteiras e reais, e de
natureza combinatória, podendo ser de difı́cil resolução. Para resolver este problema de otimização utilizou-se um algoritmo MAX-MIN Ant System - (MMAS),
uma variante do algoritmo colônia de formigas. Esta meta-heurı́stica é baseada
no comportamento social e natural das formigas reais. A principal caracterı́stica
do algoritmo implementado, é a incorporação de limites máximo e mı́nimo para
o feromônio, no algoritmo colônia de formigas (ACO). Estes limites incorporados,
têm um efeito de intensificação no processo de busca da melhor solução para obter
uma intensa exploração das soluções no espaço de busca. O objetivo do problema
de reconfiguração de sistemas de distribuição de energia elétrica é encontrar uma
topologia radial para o sistema que apresente perda ativa mı́nima, e perfis equilibrados das tensões nas barras. O Método de Soma de Potência - MSP, foi utilizado
para o cálculo do fluxo de carga e determinação das perdas de potência ativa dos
sistemas de testados. Para verificar a eficácia e robustez da metodologia implementada, foram realizados testes com sistemas de 33, 69 e 136 barras, os resultados
obtidos são comparados com os resultados encontrados na literatura.
Palavras Chave
Reconfiguração; Colônia de formigas; MAX-MIN Ant System; MMAS;
Rede de Distribuição; Perdas ativas; Fluxo de carga radial; Método da soma
de potências; MSP.
vii
viii
Abstract
Masters Dissertation
Post-Graduation Program in Electrical Engineering
Federal University of Bahia
Optimal Network Reconfiguration in Electrical Distribution System
Applying MAX-MIN Ant System Algorithm
Author: Huilman Sanca Sanca
Supervisor: Niraldo Roberto Ferreira
This work presents a methodology to solve the problem of the reconfiguration of
electrical energy distribution systems. This case can be seen as a problem of nonlinear programming of integer variables and real, and combinatorial nature, can be
difficult to resolve. To solve this optimization problem using a MAX-MIN Ant System algorithm-(MMAS), a variant of the Ant Colony algorithm. This meta-heuristic
is based on the natural and social behavior of real ants. The main characteristic of
the algorithm implemented, is the incorporation of maximum and minimum limits
for the pheromone, on ant colony algorithm (ACO). These limits incorporated has
an effect of intensifying the process of searching for the best solution, to get an
intense exploration of solutions in the search space. The objective of the problem of
reconfiguration of electrical energy distribution systems is to find a radial topology
for the system that provides active minimal loss and balanced profiles of tension
buses. The power summation method-PSM, was used to calculate the load flow and
determination of active power losses in the systems tested. To verify the effectiveness and hardiness of the methodology implemented tests with 33, 69 and 136 buses,
the results obtained are compared with the results found in the literature.
keywords
Reconfiguration; ant colony; MAX-MIN ant system; MMAS; distribution network;
active power loss; radial load flow; power summation method; PSM.
ix
x
Agradecimentos
Um desafio tão grande quanto escrever esta dissertação, foi utilizar apenas três
páginas para dar meus mais sinceros agradecimentos às instituições e às pessoas que
fizeram parte desta minha trajetória. Um espaço limitado esta secção de agradecimentos, que com certeza, não me permitirá agradecer como deveria às pessoas que,
ao longo do meu Mestrado em Engenharia Elétrica me ajudaram, direta ou indiretamente, a cumprir os meus objetivos. Desta forma, deixo apenas algumas palavras,
poucas, porém de um profundo sentimento de reconhecimento e agradecimento.
Meu Sincero Agradecimento.
Ao Prof. Dr. Jés de Jesus Fiais Cerqueira por ter me aceito durante o perı́odo
de inscrição para o programa de Mestrado em Engenharia Elétrica, por ter ajudado
a minha vinda ao Brasil. Ao professor Doutor Niraldo Roberto Ferreira orientador
deste trabalho, pela amizade e pela confiança em mim depositada quando aceitou
ser o meu orientador. Ao professor Doutor Benemar Alencar de Souza pela coorientação deste trabalho e pela ajuda que deu durante o perı́odo de intercâmbio com
a Universidade federal de Campina Grande. Obrigado professores pela dedicação e
competência demonstradas, acima de tudo, pela presença humana e cientı́fica. Dificilmente poderei com palavras expressar todos os meus sentimentos de agradecimento a estes professores, porém sem duvida nenhuma tentarei sempre aplicar os
ensinamentos que me deram, tanto na minha atuação profissional quanto na minha
vida pessoal.
Ao Professor Doutor Fermando Augusto Moreira, pela amizade, pelos incentivos
e pelas trocas de ideias.
Aos comentários e as sugestões dos membros da banca examinadora desta dissertação: Prof. Dr. Benemar Alencar de Souza, da UFCG; ao Prof. Dr. André Luı́s
de Carvalho Valente, da UFBA; e ao Prof. Dr. Renato José Pino de Araújo, da
UNIJORGE.
Muito Obrigado Professores!.
xi
• Aos Professores e Funcionários do Departamento de Engenharia Elétrica (DEE)
da Universidade Federal da Bahia - UFBA, pela amizade e cordialidade, e por
tudo que me ensinaram, contribuindo em muito para o meu aprimoramento
profissional. Especialmente à Prof.a Dr.a Luciana Martinez e ao Prof. Dr.
Evangivaldo Almeida Lima.
• Aos Professores e Funcionários do Departamento de Engenharia Elétrica do
Centro de Engenharia Elétrica e Informática da Universidade Federal de Campina Grande - UFCG, pelos ensinamentos, pela amizade e cordialidade que me
deram durante o periodo de intercâmbio. Especialmente ao Prof. Dr. Washington Luı́s de Araújo Nevis e ao Prof. Dr. Wellington Santos Mota.
• À Universidade Federal da Bahia, à Coordenação do Programa de Pós-graduação
em Engenharia Elétrica, à Coordenação de Aperfeiçoamento de Pessoal de
Nı́vel Superior (CAPES), pela concessão de uma bolsa de estudos durante a
realização do curso de mestrado; À Fundação de Amparo à Pesquisa do Estado
da Bahia (FAPESB).
• Aos colegas e amigos que tive a oportunidade de conhecer durante o curso de
mestrado na UFBA, em especial aos do DEE.
• A todos os amigos que conviveram comigo no Laboratório de Sistemas Potência,
pelo companheirismo e respeito mútuo, Leroy Umasi Ramos, Jose Antônio Sobrinho de Sousa e Romel França.
Meu Agradecimento Especial
• A Deus o Único cujo nome é Jeová, por ter me dado uns maravilhosos pais,
Juan Sanca Apaza y Victoria Melina Sanca de Sanca, a ellos por lo
más valioso que supieron darme, la vida, por darme tan ejemplar educación y
por todo el esfuerzo que hicieron por mı́, por tantas penurias que tuvieron que
pasar y tantos dı́as de trabajo sin descanso, solo con el único fin de darnos lo
que de repente la vida no supo darles a ellos, todo esto les debo y que ni con
una vida entera podre recompensarles, valió la pena tanto esfuerzo, desde el
fondo de mi corazón gracias papá y mamá.
• A toda mi familia que son tan especiales como lo son mis padres, a mis hermanos Nancy Karina, Ruben a su esposa Gretty y a mi sobrinito André
Marcelo, gracias hermanos por soportar mi ausencia. Y agradezco de especial forma a mi hermano Armando por ser como eres y por mostrarnos a todos
nosotros tus hermanos el camino del estudio y la sabiduria, tu representas para
mı́ el pilar más importante del conocimiento. E como esquecer de dar meus
agradecimentos à esposa de Armando, Ana Lı́gia, que eu acho que ela teve,
ainda mais do que eu, a Fé de que eu possa chegar ao Brasil, obrigado Aninha
pela força, agradeço também a sua famı́lia, Graça Lago, Claudia, Ana Raquel,
xii
Charles Lago e a todos aqueles que conheci e que souberam me receber como
se fosse parte da sua própria famı́lia. Gracias Dios mı́o por conocer a todas
estas personas tan especiales en mi vida y que me diste el gusto y la honra de
llamarlos FAMILIA!.
• Aos meus amigos de Salvador, Omar Alexander Chura Vilcanqui, Elvis Zevallos à esposa dele Rosário e aos seus filhos, agradeço também a Antônio
Sobrinho, Carolina Moreno, Wilton La Cerda, Ademário Carvalho, Aston,
Miguel Pereira, Cersar Peña, Francis Mari Noronha, Sandra Aleluia, Eduardo
Andrade, Lucas Lima. Aos meus amigos de Campina Grande, especialmente a
José do Pratrocı́nio Santos Silva a Alyson Henrique, João Campos, Boris Alva,
obrigado pela ajuda, pelo apoio, e por tantas coisas que, por vezes, somente
bons amigos podem fazer por nós.
A todos os amigos que, direta ou indiretamente, contribuı́ram para a realização
desta conquista,
Muito obrigado mesmo!
Salvador-BA, 26 de Julho de 2013.
Huilman Sanca Sanca.
xiii
xiv
Índice
Resumo
vii
Abstract
ix
Agradecimentos
xi
Índice
xv
Lista de Figuras
xix
Lista de Tabelas
xxi
Nomenclatura Matemática
xxiii
1 Introdução
1.1 Reconfiguração de sistemas de distribuição
1.2 Motivação . . . . . . . . . . . . . . . . . .
1.3 Objetivo . . . . . . . . . . . . . . . . . . .
1.4 Contribuições e Propostas da Dissertação .
1.5 Estrutura do Texto . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
2
4
4
4
5
2 Revisão Bibliográfica
2.1 Introdução . . . . . . . . . . . . . . . . . . . . . .
2.2 Metodologias e principais trabalhos publicados . .
2.2.1 Heurı́sticas . . . . . . . . . . . . . . . . . .
2.2.2 Redes Neurais Artificiais . . . . . . . . . .
2.2.3 Algoritmos Genéticos . . . . . . . . . . . .
2.2.4 Têmpera Simulada (Simulated Annealing)
2.2.5 Busca Tabu (Tabu Search) . . . . . . . . .
2.2.6 Nuvem de Partı́culas (Particle swarm) . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
7
7
8
8
10
11
11
12
12
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3 Meta-heurı́stica Colônia de Formigas
15
3.1 Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
3.2 Inspiração Biológica . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
xv
3.3
Otimização por Colônia de Formigas . . . . . . . . . . . . . . . . .
3.3.1 Colônia de formigas aplicado ao problema do caixeiro viajante
(Traveling salesman problem - TSP) . . . . . . . . . . . . .
Colônia de Formigas . . . . . . . . . . . . . . . . . . . . . . . . . .
3.4.1 Ant System - AS . . . . . . . . . . . . . . . . . . . . . . . .
3.4.2 Elitist Ant System - EAS . . . . . . . . . . . . . . . . . . .
3.4.3 Ant Colony System - ACS . . . . . . . . . . . . . . . . . . .
3.4.4 MAX-MIN Ant System - MMAS . . . . . . . . . . . . . . .
Aplicação do Algoritmo Colônia de Formigas . . . . . . . . . . . . .
3.5.1 Problema de Reconfiguração de Sistemas de Distribuição de
Energia Elétrica . . . . . . . . . . . . . . . . . . . . . . . . .
Conclusão do Capı́tulo . . . . . . . . . . . . . . . . . . . . . . . . .
. 18
4 Metodologia Proposta
4.1 Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2 Formulação do problema . . . . . . . . . . . . . . . . . . . . . . . .
4.3 Algoritmo MAX-MIN Ant System - MMAS . . . . . . . . . . . . .
4.3.1 O Paradigma do Algoritmo MAX-MIN Ant System Utilizada
para a Reconfiguração de Sistemas de Distribuição de Energia
Elétrica . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.2 Regra de Transição de Estado . . . . . . . . . . . . . . . . .
4.3.3 Regra de Atualização do Feromônio . . . . . . . . . . . . . .
4.3.4 Limites de Feromônio . . . . . . . . . . . . . . . . . . . . . .
4.4 Exemplo de Busca das configurações radiais . . . . . . . . . . . . .
29
. 29
. 30
. 31
3.4
3.5
3.6
5 Fluxo de Carga
5.1 Introdução . . . . . . . . . . . . . . . . . . . . . . . . . .
5.2 Fluxo de Carga para Sistemas de Distribuição de Energia
5.2.1 Modelo da Rede de Distribuição . . . . . . . . . .
5.2.2 Método de Soma de Potências - MSP . . . . . . .
5.3 Teste Fluxo de Carga MSP . . . . . . . . . . . . . . . .
5.3.1 Sistema de 33 barras . . . . . . . . . . . . . . . .
5.3.2 Sistema de 69 barras . . . . . . . . . . . . . . . .
5.3.3 Sistema de 136 barras . . . . . . . . . . . . . . .
5.4 Conclusão do Capı́tulo . . . . . . . . . . . . . . . . . . .
6 Testes e Resultados
6.1 Estudo de Casos . . . . . .
6.2 Sistema Teste de 33 barras .
6.3 Sistema Teste de 69 barras .
6.4 Sistema Teste de 136 barras
6.5 Conclusão do Capı́tulo . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
xvi
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . .
Elétrica
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
. . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
18
20
20
23
23
24
25
. 25
. 27
.
.
.
.
.
31
32
33
34
36
.
.
.
.
.
.
.
.
.
43
43
44
44
44
51
51
52
53
55
.
.
.
.
.
57
57
58
61
64
68
7 Conclusões e Trabalhos Futuros
69
7.1 Sugestões de Futuros Trabalhos . . . . . . . . . . . . . . . . . . . . . 70
Referências Bibliográficas
71
A Divulgação da Pesquisa
77
B Dados dos Sistemas Testados
79
B.1 Sistema de 33 barras . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
B.2 Sistema de 69 barras . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
B.3 Sistema de 136 barras . . . . . . . . . . . . . . . . . . . . . . . . . . 83
xvii
xviii
Lista de Figuras
1.1 Sistema elétrico de potência, geração, transformação e distribuição. .
2
3.1 Experimento ponte de cumprimentos iguais. . . . . . . . . . . . . . . 17
3.2 Experimento ponte de cumprimentos diferentes. . . . . . . . . . . . . 18
3.3 Resultado obtido para o problema do caixeiro viajante Traveling Salesman Problem - TSP para 30 cidades aplicando sistema de formigas
Ant System - AS (Dorigo et al., 1991). . . . . . . . . . . . . . . . . . 19
4.1 Exemplo de uma colônia de formigas real explicando o comportamento delas na procura de alimento. . . . . . . . . . . . . . . . . . .
4.2 Sistema fictı́cio de 5 barras, rede malhada. . . . . . . . . . . . . . . .
4.3 Sistema fictı́cio de 5 barras na inicialização do processo, (a) sistema
com os trechos não ativados, (b) trechos adjacentes (ativáveis) por
onde a formiga pode se movimentar. . . . . . . . . . . . . . . . . . .
4.4 Roleta aleatória para escolha entre os trechos 1-2 e 1-3. . . . . . . . .
4.5 Sistema fictı́cio de 5 barras, deslocamento do agente desde a barra 1
até a barra 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.6 Roleta aleatória para escolha entre os trechos 1-2, 3-2, 3-4 e 3-5. . . .
4.7 Sistema fictı́cio de 5 barras, deslocamento do agente desde a barra 3
até a barra 4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.8 Roleta aleatória para escolha entre os trechos 1-2, 3-2, 3-5, 4-2 e 4-5. .
4.9 Sistema fictı́cio de 5 barras, deslocamento do agente desde a barra 3
até a barra 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.10 Roleta aleatória para escolha entre os trechos 1-2, 3-2 e 4-2. . . . . .
4.11 Sistema fictı́cio de 5 barras na inicialização do processo, (a) deslocamento do agente desde a barra 1 até a barra 2, (b) uma das configurações radiais encontrada. . . . . . . . . . . . . . . . . . . . . . .
4.12 Fluxograma do Max-Min Ant System - MMAS para reconfiguração
de sistemas de distribuição de energia elétrica. . . . . . . . . . . . . .
32
37
37
38
38
39
39
40
40
41
41
42
5.1 Exemplo de um sistema de distribuição de energia elétrica radial. . . 45
5.2 Rede distribuição radial. . . . . . . . . . . . . . . . . . . . . . . . . . 46
5.3 Trecho da rede distribuição radial para a aplicação do método de
soma de potências. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
xix
5.4
5.5
5.6
5.7
Algoritmo do fluxo de carga método de soma de potências - MSP, do
tipo Backward - Forward. . . . . . . . . . . . . . . . . . . . . . . .
Perfil da tesão para a configuração inicial do sistema de 33 barras. .
Perfil da tesão para a configuração inicial do sistema de 69 barras. .
Perfil da tesão para a configuração inicial do sistema de 136 barras.
6.1
6.2
.
.
.
.
Configuração inicial do sistema de distribuição de 33 barras e 37 ligações.
Evolução do processo de convergência do algoritmo MMAS, perdas
totais versus expedições, sistema de 33 barras. . . . . . . . . . . . . .
6.3 Comparação do perfil da tensão em cada barra da configuração inicial
e da configuração final encontrada pelo algoritmo MAX-MIN Ant
System - MMAS implementado, sistema de 33 barras. . . . . . . . . .
6.4 Rede de distribuição reconfigurada obtida pelo algoritmo MAX-MIN
Ant System - MMAS implementado, sistema de 33 barras. . . . . . .
6.5 Configuração inicial do sistema de distribuição de 69 barras e 73 ligações.
6.6 Evolução do processo de convergência do algoritmo MMAS, perdas
totais versus expedições, sistema de 69 barras. . . . . . . . . . . . . .
6.7 Comparação do perfil da tensão em cada barra da configuração inicial
e da configuração final encontrada pelo algoritmo MAX-MIN Ant
System - MMAS implementado, sistema de 69 barras. . . . . . . . . .
6.8 Rede de distribuição reconfigurada obtida pelo algoritmo MAX-MIN
Ant System - MMAS implementado, sistema de 69 barras. . . . . . .
6.9 Configuração inicial do sistema de distribuição de 136 barras e 156
ligações. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.10 Evolução do processo de convergência do algoritmo MMAS, perdas
totais versus expedições, sistema de 136 barras. . . . . . . . . . . . .
6.11 Comparação do perfil da tensão em cada barra da configuração inicial
e da configuração final encontrada pelo algoritmo MAX-MIN Ant
System - MMAS implementado, sistema de 136 barras. . . . . . . . .
6.12 Rede de distribuição reconfigurada obtida pelo algoritmo MAX-MIN
Ant System - MMAS implementado, sistema de 136 barras. . . . . . .
xx
50
51
53
54
59
59
61
61
62
62
64
64
65
66
67
68
Lista de Tabelas
5.1
5.2
5.3
5.4
5.5
Relação R/X para diversos valores de tensão . . . . . . . . .
Tensões da configuração inicial para o sistema de 33 barras.
Tensões da configuração inicial para o sistema de 69 barras.
Tensões da configuração inicial para o sistema de 136 barras,
Tensões da configuração inicial para o sistema de 136 barras,
. . .
. . .
. . .
(a).
(b).
.
.
.
.
.
6.1 Parâmetros utilizados para o algoritmo nos sistemas de distribuição
testados. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.2 Comparação de resultados obtidos para a reconfiguração do sistema
de 33 barras. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.3 Comparação de resultados obtidos para a reconfiguração do sistema
de 69 barras. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.4 Comparação de resultados obtidos para a reconfiguração do sistema
de 136 barras. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
B.1
B.2
B.3
B.4
B.5
B.6
B.7
Dados
Dados
Dados
Dados
Dados
Dados
Dados
do
do
do
do
do
do
do
sistema
sistema
sistema
sistema
sistema
sistema
sistema
de
de
de
de
de
de
de
33 barras. . . . . . . . .
69 barras, parte 1 de 2. .
69 barras, parte 2 de 2. .
136 barras, parte 1 de 4.
136 barras, parte 2 de 4.
136 barras, parte 3 de 4.
136 barras, parte 4 de 4.
xxi
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
44
51
52
53
54
. 58
. 60
. 63
. 67
.
.
.
.
.
.
.
80
81
82
83
84
85
86
xxii
Nomenclatura Matemática
A menos que referência contrária seja fornecida, os sı́mbolos matemáticos abaixo
possuem os seguintes significados:
P robk
η(i,j)
Jk
α
β
dij
m
Q
Lk
∆τ (i, j)
W
e
C bs
q
q0
J
ρ
∆τ best
ξ
P rob
η(i,j)
τ0
τ(i,j)
Jk
PT,perdas
|Ii |
Probabilidade de que a formiga k escolha o caminho (i, j).
E uma informação previa (heurı́stica) do problema, um ı́ndice
de atratividade de escolha pelo caminho (i, j).
Conjuntos das cidades ainda não visitadas pela formiga k.
Peso da concentração de feromônio.
Peso da informação heurı́stica do problema.
Distancia entre as cidades (i, j).
Número de formigas.
Constante de peso para o depósito de feromônio.
Comprimento da rota da k-ésima formiga.
Depósito de feromônio das formigas para o caminho (i, j).
Valor constante.
Parâmetro que define o peso ao T bs .
Comprimento do menor caminho encontrado.
Número aleatório de intervalo [0, 1].
Parâmetro com valor: 0 ≤ q0 ≤ 1.
Regra de probabilidade.
Parâmetro de decaimento do feromônio.
Depósito de feromônio para o melhor caminho.
Parâmetro de decaimento do feromônio, variando entre zero e um.
Probabilidade que um trecho (i, j) seja escolhida.
E uma informação prévia (heurı́stica) do problema, um ı́ndice
de atratividade de escolha pelo caminho (i, j).
Parâmetro com o valor inicial da trilha de feromônio.
Quantidade de feromônio na ligação escolhida (i, j).
Conjuntos de barras ainda não visitadas pela formiga k.
é a perda de potência ativa total do sistema.
Amplitude da corrente no trecho.
xxiii
Ii,max
NB
NT
Fmelhor
Pbest
λI
Vi ∠δi
Vi+1 ∠δi+1
Ii+1 ∠θi+1
Ri,i+1
jXi,i+1
PLi + jQLi
PLi+1
QLi+1
Pi+1
Qi+1
∆Pi+1
∆Qi+1
Limite máximo de corrente em cada trecho i.
é o número de barras do sistema.
é o conjunto de trechos de linha do sistema.
Melhor solução da iteração.
Probabilidade de uma formiga construir o melhor caminho.
Fator de penalidade com respeito à corrente admissı́vel no trecho.
Tensões (módulo e ângulo) das barras i.
Tensões (módulo e ângulo) das barras i + 1.
Corrente que atravessa o trecho (i, i + 1).
Resistência do trecho (i, i + 1).
Reatância do trecho (i, i + 1).
Carga instalada em cada barra i.
Carga ativa instalada em cada barra i + 1.
Carga reativa instalada em cada barra i + 1.
Fluxo de carga de potência ativa do trecho i + 1.
Fluxo de carga de potência reativa do trecho i + 1.
Fluxo de potência ativa chegando para o trecho i + 1.
Fluxo de potência reativa chegando para o trecho i + 1.
xxiv
Capı́tulo 1
Introdução
A
ENERGIA elétrica tornou-se um produto indispensável, proporcionando avanço
tecnológico que no Brasil impulsiona um mercado altamente competitivo,
exigindo que as empresas concessionárias de energia elétrica adotem medidas para
aumentar a eficiência, tanto na gestão administrativa como na técnica. É por isso, as
empresas do setor colocam esforços em realizar uma correta operação do sistema com
a finalidade de promover e fornecer um serviço adequado, eficiente e de qualidade.
A função dos sistemas elétricos de potência consiste em fornecer energia elétrica
aos usuários com a qualidade adequada. Para desempenhar esta função deve-se
produzir a energia e distribuı́-la. Os sistemas de energia elétrica podem ser divididos
em três grandes grupos conforme a Figura 1.1: Geração, Transmissão e Distribuição.
A geração compreende os centros produtores de energia elétrica como as usinas
hidrelétricas, e tem a função de converter de alguma forma energia potencial em
energia elétrica. A transmissão é a responsável do transporte da energia gerada,
desde os centros de produção aos centros de consumo ou de distribuição. As redes de
distribuição primária ou redes de média tensão saem das subestações de distribuição
e operam normalmente em configuração radial. Estas redes atendem a os consumidores primários (industriais de porte médio, conjuntos comerciais e residenciais,
entre outros).
Sistemas de distribuição de energia elétrica devem operar de forma confiável e
econômica, respeitando tanto as restrições de carga como as restrições operacionais
(Cavellucci, 1998). O primeiro tipo de restrição está relacionado com o suprimento
da demanda total dos consumidores alimentados pelo sistema, enquanto que o se1
2
Capı́tulo 1. Introdução
Geração
Transmissão
Distribuição
Figura 1.1: Sistema elétrico de potência, geração, transformação e distribuição.
gundo estabelece os limites de tensão e corrente para garantir que as linha e os
equipamentos instalados operem de forma segura e eficiente.
Uma vez que o sistema está operando em regime permanente, é desejável aumentar
sua eficiência e diminuir seu custo operacional. Uma das formas de se obter este
resultado é através da operação do sistema no estado de mı́nimas perdas. Neste
estado o sistema de distribuição apresenta um melhor perfil de tensão ao longo
dos alimentadores, caracterizada por uma melhor distribuição do fluxo de potência
nas linhas, o que influencia diretamente no aumento da vida útil dos equipamentos
instalados na rede (Cavellucci, 1998).
Cabe mencionar que existem exemplos de algumas técnicas para reduzir as perdas
de energia elétrica nas redes de distribuição, as mais importantes são, provavelmente
o aumento do nı́vel de tensão da rede, o recondutoramento total ou parcial do
sistema e a reconfiguração da rede de distribuição elétrica. Dentre estas técnicas,
a reconfiguração é a técnica mais atrativa para a empresa distribuidora de energia
elétrica, pois permite a utilização de recursos já existentes no sistema.
1.1
Reconfiguração de sistemas de distribuição
A reconfiguração de sistemas de distribuição de energia elétrica tem o objetivo
de encontrar a melhor topologia para o sistema de distribuição através da abertura
e fechamento de chaves de interconexões respeitando sempre que a topologia final
achada seja radial (Civanlar et al., 1988; Nara et al., 1992). A reconfiguração é
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 1.1. Reconfiguração de sistemas de distribuição
3
um procedimento realizado principalmente, visando minimizar as perdas ativas do
sistema, melhorar o perfil da tensão nas barras, manter a confiabilidade do sistema,
fazer isolamento rápido quando acontecer faltas e realizar manutenção preventiva
do sistema. Os chaveamentos são utilizados para manter o controle sobre a rede,
e assegurar a operação dentro de padrões de qualidade de fornecimento de energia
elétrica (Guimarães, 2005).
O problema de reconfiguração é de natureza combinatória e pode ser modelado
como um problema de programação não linear inteiro (PNLI), cujo objetivo é minimizar as perdas de potência ativa no sistema elétrico, sujeito às restrições essenciais
para a operação do sistema como a condição de radialidade, limites de corrente nos
circuitos (Civanlar et al., 1988; Baran e Wu., 1989; Ching-Tzong et al., 2005; Pereira
et al., 2006; Chung-Fu, 2008; Ding e Loparo, 2012). A dimensão do problema está
relacionada ao número de chaves envolvidas na busca de uma configuração ótima.
Dado um sistema com X chaves, existem 2X possı́veis configurações correspondendo
às posições aberta e fechada de todas as chaves no sistema (Pereira et al., 2006).
Algumas destas configurações não são permitidas, por não satisfazerem a restrição
de radialidade, ou não são factı́veis, por violarem restrições operacionais. Por outro
lado, o problema cresce exponencialmente com a quantidade e disposição destes
dispositivos.
Nas últimas décadas, tem sido crescente a atenção a algoritmos inspirados na observação de fenômenos naturais para ajudar a resolver os complexos problemas combinatórios da engenharia moderna. O algoritmo colônia de formigas - ACO é uma
meta-heurı́stica utilizada para resolver este tipo de problemas de otimização combinatória. Esta meta-heurı́stica foi aplicada pela primeira vez ao problema clássico
do caixeiro viajante, Traveling Salesman Problem - TSP (Dorigo e Stutzle, 2004) e
mais tarde aplicado para resolver o problema de configuração de redes (Ching-Tzong
et al., 2005; Charles et al., 2005; Pereira et al., 2006; Zhijiam et al., 2008; ChungFu, 2008). O algoritmo colônia de formigas é inspirado no comportamento das
formigas, em particular, como é conhecido, as formigas são capazes de encontrar
o caminho mais curto a partir do formigueiro para a fonte de alimento sem a utilização de sinais visuais, o meio de comunicação das formigas ocorre mediante uma
substância quı́mica depositada por elas chamada de feromônio.
3
4
Capı́tulo 1. Introdução
1.2
Motivação
Nas últimas décadas, tem sido crescente a atenção em algoritmos inspirados na
observação de fenômenos naturais para ajudar a resolver os complexos problemas
combinatórios da engenharia moderna.
A exigência que as empresas concessionárias de energia elétrica adotem medidas
para aumentar a eficiência, tanto na gestão administrativa como na técnica. É por
isso, as empresas do setor colocam esforços em realizar uma correta operação do
sistema com a finalidade de fornecer um serviço adequado eficiente e com qualidade.
1.3
Objetivo
Este trabalho tem por objetivo principal o desenvolvimento de um algoritmo de
reconfiguração baseado em colônia de formigas MAX-MIN Ant system objetivando
a redução das perdas de potência ativa do sistema de distribuição de energia elétrica
radial.
Assim também como objetivos secundários temos:
• Estudar e implementar o algoritmo MAX-MIN Ant System aplicado para reconfiguração de sistemas de distribuição de energia elétrica.
• Encontrar uma configuração radial dos sistemas testados que apresente um
menor valor de perdas de potência ativa com respeito ao valor inicial.
• Realizar comparações dos resultados obtidos com outros métodos que foram
aplicados na literatura.
1.4
Contribuições e Propostas da Dissertação
Uma metodologia para resolver o problema de reconfiguração de sistemas de distribuição de energia elétrica mediante o uso de uma variante do algoritmo colônia
de formigas, o MAX-MIN Ant system - MMAS (Dorigo et al., 1996; Dorigo e Gambardella, 1997; Stutzle e Hoos, 2000) é apresentado. Esse algoritmo tem como principal caracterı́stica a intensa exploração em torno das melhores soluções encontradas.
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 1.5. Estrutura do Texto
5
Outra caracterı́stica do MMAS é a existência de limites superior e inferior para
a taxa de feromônio. Esses limites foram introduzidos para evitar a convergência
precoce do algoritmo.
1.5
Estrutura do Texto
O texto está organizado da seguinte forma:
• O capı́tulo 2 apresenta a revisão bibliográfica, os conceitos teóricos preli-
minares necessários para a compreensão do conteúdo desta dissertação objetivando descrever as principais heurı́sticas e métodos da otimização aplicados
ao problema da reconfiguração de sistemas de distribuição.
• No capı́tulo 3, é apresentado o algoritmo colônia de formigas e alguns dos
métodos mais conhecidos baseados na sua estrutura, assim também é mostrado
alguns trabalhos que utilizaram este algoritmo para resolver problemas de
reconfiguração.
• No capı́tulo 4, é apresentado o algoritmo MAX-MIN Ant System - MMAS
implementado neste trabalho para resolver o problema de reconfiguração de
sistemas de distribuição de energia elétrica.
• No capı́tulo 5, é apresentado uma breve introdução aos cálculos de fluxo de
carga utilizado neste trabalho.
• O capı́tulo 6 são apresentados os sistemas de distribuição testados e resultados
obtidos pela metodologia implementada.
• O capı́tulo 7 apresenta as conclusões e sugestões de trabalhos futuros.
• O apêndice A apresenta a divulgação da pesquisa (artigos publicados deco-
rrentes deste trabalho), e no apêndice B é apresentado os dados dos sistemas
testados.
5
6
Huilman Sanca Sanca - Dissertação de Mestrado
Capı́tulo 1. Introdução
Capı́tulo 2
Revisão Bibliográfica
O capı́tulo a seguir apresenta uma revisão dos conceitos teóricos preliminares necessários para compreensão do conteúdo da dissertação, objetivando o estudo dos principais métodos aplicados para reconfiguração de
redes de distribuição de energia elétrica. Apesar de ter sido proposta há
mais de 30 anos, a reconfiguração de redes de distribuição para redução
de perdas ativas ainda faz parte de pesquisas onde várias técnicas têm
sido propostas ao longo dos anos.
2.1
E
Introdução
NERGIA elétrica tornou-se, ao longo dos anos, um produto indispensável ao
desenvolvimento humano. Descobrir novas fontes de energia disponı́vel onde for
necessário, converter a energia de uma forma para outra e usá-la sem criar poluição
que destruirá nossa biosfera são, entre os outros, os maiores desafios enfrentados
pelo mundo de hoje.
O sistema elétrico de potência é composto de centrais geradoras, linhas de transmissão e os sistemas de distribuição, e é a principal ferramenta para converter,
transportar e distribuir energia elétrica. Em grande parte do século passado foram
realizadas pesquisas voltados ao planejamento da geração e transmissão de energia
devido a sua complexidade por que apresentaram muitos desafios. Com o aumento
do consumo de energia elétrica o planejamento e a operação exigiram novas técnicas
de análise para uma adequada operação do sistema.
7
8
Capı́tulo 2. Revisão Bibliográfica
Os problemas de otimização relacionados ao planejamento e operação de sistemas
de distribuição são complexos, tanto pelas próprias caracterı́sticas das redes, quanto
pelo grande número de variáveis. Neste trabalho será abordado o problema de
reconfiguração de redes de distribuição primária como um problema de otimização,
cujo objetivo é minimizar as perdas ativas do sistema. Este problema de otimização
é um exemplo de problema de Programação Não-linear Inteira Mista - PNLIM e
apresenta o fenômeno de explosão combinatória.
No capı́tulo a seguir serão analisadas as principais teorias propostas existentes na
literatura dos primeiros métodos utilizados para a reconfiguração dos sistemas de
distribuição de energia elétrica.
2.2
Metodologias e principais trabalhos publicados
Várias metodologias tem sido propostas para a solução de problemas de PNLIM,
que são como já mencionados, difı́ceis de resolver, considerando que apresenta uma
natureza combinatória elevada e muitas soluções locais ótimas podem ser encontrados.
2.2.1
Heurı́sticas
Branch and Bound
É uma técnica que pode ser utilizada na resolução de problemas de programação
inteira mista. Consiste em um método de programação exata, portanto, capaz de
obter o ótimo global (Merlin e Back, 1975). Contudo, para sistemas de grande porte
torna-se inviável.
Em 1875 os franceses Merlin e Back apresentaram uma das primeiras propostas
especializadas para reconfiguração de redes de distribuição de energia elétrica para
diminuição de perdas ativas que aparece na literatura. Considera-se uma configuração inicial em malha em que todas as chaves de interconexão existentes no
sistema estão fechadas. A partir desta configuração, o algoritmo desenvolvido determina a abertura sequencial das chaves até que se tenha uma configuração com
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 2.2. Metodologias e principais trabalhos publicados
9
menores perdas.
Duas metodologias heurı́sticas foram aplicadas para resolver o problema de reconfiguração de sistemas de distribuição: a primeira metodologia foi a aplicação de
uma técnica de otimização clássica (Bueno, 2005) e a segunda metodologia utiliza
um algoritmo heurı́stico construtivo (H. back) 1 .
A primeira é a metodologia denominada Busca Menor Energia, inspirada na
técnica de abertura sequencial de chaves. A segunda técnica, denominada árvore
de aproximação, faz uso das idéias de árvore geradora de custo mı́nimo. Ambas
são combinadas com uma busca local, denominada Troca de Ramos Generalizada,
baseada na técnica de Troca de Ramos.
Um método heurı́stico simples em que utilizam uma técnica de busca em árvores
do tipo branch and bound para encontrar o conjunto das melhores configurações
para redes radiais foi apresentado em (Mantovani et al., 2000). Onde apresentam
um método de cálculo de fluxo de potência radial rápido e eficiente, além de um
critério de corte para reduzir o espaço de busca de configurações baseado no limite
máximo de queda de tensão permitido na rede.
Troca de Ligações (Branch Exchange)
Esta metodologia Branch Exchange ou troca de ligações é conhecida como heurı́stica
construtiva, é um método utilizado no problema de reconfiguração de redes de distribuição. Sendo heurı́stico não garante a solução ótima global, mas pode conduzir a
ótimos locais. Esta proposta consiste na avaliação de configurações radiais, geradas
a partir de uma configuração inicial através da abertura e fechamento de chaves
(Civanlar et al., 1988).
Civanlar et al., (1988) propõem uma metodologia heurı́stica para ser utilizada
como ferramenta tanto de planejamento como de controle e restauração de alimentadores primários objetivando a redução de perdas ativas. A proposta de solução
possui a capacidade de estimar, com mı́nimo esforço computacional, as mudanças nas
perdas que resultam da reconfiguração dos alimentadores. Utilizam, como critério
para reduzir o número de reconfigurações candidatas, uma fórmula interessante e
1
Merlin, A.; H. Back. (1975).Search for a Minimal-Loss operating spanning tree configuration in
an urban power distribution system. In Proceedings of 5th Power System Computation Conference.
- PSCC, Cambridge, U.K., v.1, p. 1-18
9
10
Capı́tulo 2. Revisão Bibliográfica
de uso simples que exclui opções indesejadas de chaveamentos sem a necessidade
de efetuar numerosos cálculos de fluxo de potência, reduzindo significativamente o
esforço computacional.
Baran e Wu., (1989) tratam do problema de reconfiguração de redes de distribuição para redução de perdas e balanceamento de cargas entre os alimentadores,
utilizando a aproximação proposta por Civanlar para abertura dos laços e realização
das operações de chaveamento. A idéia básica de busca da metodologia é que a partir de uma configuração factı́vel, fechar no primeiro nı́vel as chaves abertas uma a
uma (Baran e Wu., 1989). Então, é escolhida a configuração que, pela troca de
um ramo, tem a maior redução das perdas. A configuração escolhida passa para o
próximo nı́vel. Como pode ser notado, a busca não examina todas as possibilidades
e dessa maneira esta metodologia não garante uma solução ótima global.
Morelato e Monticelli (1989) nesta linha de pesquisa da operação on-line de redes
de distribuição apresentam uma estratégia de busca direcionada com a utilização de
regras práticas (baseadas na experiência dos operadores), para resolver problemas
como restauração do serviço de fornecimento de energia e reconfiguração de sistemas.
Uma técnica de busca heurı́stica em árvore de decisão binária (Morelato e Monticelli,
1989), que permite percorrer o espaço de possibilidades dos estados das chaves do
sistema, enquanto que o conhecimento de domı́nio especı́fico (regras práticas) é
essencial para limitar o tamanho da árvore, evitando uma explosão combinatória,
mantendo o problema dentro de um espaço de busca de dimensão gerenciável.
2.2.2
Redes Neurais Artificiais
Em 1993 os autores Kim et al., (1993) propuseram a resolução do problema de reconfiguração através de Redes Neurais Artificiais do tipo Perceptron multi-camadas,
Este método tem a capacidade de controle em tempo real do sistema de distribuição,
com relação a outros métodos. A rapidez do método é devido ao fato da rede neural
ser treinado utilizando um conjunto de boas configurações para diferentes valores
de carregamento (Kim et al., 1993). Para diminuir o esforço computacional o sistema de distribuição foi dividido em três tipos, residencial, comercial e industrial,
facilitando o treinamento da rede neural.
Em 2006, Salazar et al., (2006) apresentaram uma rede neural artificial do tipo
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 2.2. Metodologias e principais trabalhos publicados
11
Perceptron Multicamadas. Eles aplicaram técnicas de agrupamento, associado a
técnicas de validação para identificar as melhores topologias utilizadas no treinamento da rede neural. Isto possibilitou determinar boas topologias com baixo custo
computacional e utilizando apenas uma rede neural durante a resolução do problema
(Salazar et al., 2006).
2.2.3
Algoritmos Genéticos
A aplicação do algoritmo genético para o problema de reconfiguração foi aplicado
por Nara, Lin e Zhu. Os trabalhos descrevem um indivı́duo do algoritmo genético
como sendo uma solução para o problema de reconfiguração. A população inicial é
escolhida aleatoriamente para os trabalhos (Nara et al., 1992; Lin et al., 2000; Zhu,
2002).
Shim et al., 2004 utilizaram um algoritmo genético combinado com o algoritmo de
busca tabu, denominado de algoritmo genético−tabu aproximado para o problema
de restauração e reconfiguração ótima de redes considerando o custo de confiabilidade (Shin et al., 2004). O método visa reduzir os custos relacionados às perdas
nos alimentadores e à interrupção do fornecimento de energia sem violar os limites
de operação do sistema. Para avaliar o custo de interrupção, os ı́ndices básicos de
confiabilidade tais como taxa de falha e duração da interrupção devem ser calculados
com antecedência.
2.2.4
Têmpera Simulada (Simulated Annealing )
Annealing é um tratamento térmico, utilizado pelos fı́sicos na construção de
cristais perfeitos. Aonde um material é exposto a altas temperaturas até o ponto
de liquefação e logo após é lentamente esfriado, mantendo durante o processo o
chamado quase equilı́brio termodinâmico. O processo termina quando o material
atinge um estado de energia mı́nimo, no qual se transforma em um cristal perfeito.
Em 1990 os autores Chinag e Jean-Jumeau publicaram um trabalho dividido em
duas partes (Chiang e Jean-Jumeau, 1990a, 1990b), que utiliza a meta heurı́stica
simulated annealing para resolver o problema de reconfiguração. Na primeira parte
do trabalho os autores tratam da formulação do problema e da metodologia de
solução e na segunda parte é tratado o algoritmo e demonstrado sua aplicação
11
12
Capı́tulo 2. Revisão Bibliográfica
(Chiang e Jeam-Jumeau, 1990). Os autores modificaram a meta-heurı́stica, inserindo nesta uma função para monitorar as restrições impostas pelo problema de
reconfiguração.
Chang e Kuo, Jeon e Parada, utilizaram a meta-heurı́stica simulated annealing na
resolução do problema de reconfiguração que tenha as menores perdas e uma topologia radial. Nestes trabalhos foram apresentados cálculos da perdas aproximadas
do sistema em conjunto com uma perturbação eficiente da temperatura (Chang e
Kuo, 1994; Jeon et al., 2002; Parada et al., 2004).
2.2.5
Busca Tabu (Tabu Search)
Toune et al., (1998) propõem o método denominado Tabu Search Reactive - RTS
para solução do modelo de restauração de serviço em sistemas de distribuição. O
RTS é um procedimento de busca tabu, Tabu Search - TS, convencional melhorado
(Toune et al., 1998), ou seja, ele possui a capacidade de ajustar os parâmetros
do algoritmo durante o procedimento da busca. Desta forma, evita uma grande
desvantagem da busca tabu convencional que é a questão dos parâmetros fixos.
O método apresentado gera um estado inicial sub-ótimo no espaço de soluções,
através de um procedimento heurı́stico. Os vizinhos do espaço de solução são gerados
através do remanejamento de cargas entre as subestações. Os estados de busca são
armazenados em uma lista tabu.
2.2.6
Nuvem de Partı́culas (Particle swarm)
A otimização por nuvem de partı́culas Particle Swarm Optimization - PSO é a
nova técnica de computação evolucionária estudada pela primeira vez por Kennedy
e Eberhart em (Eberhart e Shi, 2001). Como outras técnicas de busca estocastica,
o PSO é inicializado com a geração de uma população de soluções aleatórias, que é
chamado de um enxame. Nesta técnica, cada solução candidato está associado a um
vetor de velocidade (Eberhart e Shi, 2001; Hu et al., 2004). O vetor de velocidade é
constantemente ajustada de acordo com a experiência de partı́culas correspondente
e também as partı́culas acompanhantes experiências.
Olamaei et al., (2007) utilizaram o algoritmo nuvem de partı́culas na resolução
do problema de operação ótima de sistemas de distribuição. Nestes trabalhos foram
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 2.2. Metodologias e principais trabalhos publicados
13
apresentados um cálculo da perda aproximada do sistema e uma avaliação econômica
para a implementação (Olamaei et al., 2007). A principal caracterı́stica do trabalho
é que o autor aplica o algoritmo num ambiente (sistema de distribuição) com geração
distribuı́da.
Lu et al., (2009) aplicaram uma modificação do algoritmo base o poly particle
swarm optimization (Lu et al., 2009), que aborda uma estrutura hierárquica do
sistema de distribuição. Os autores realizaram uma análise separada de sub sistemas,
o que segundo eles poderia reduzir a dimensão do espaço de busca do problema de
reconfiguração e só a melhor posição encontrada por cada subsistema foi considerada
como a melhor posição da partı́cula.
13
14
Huilman Sanca Sanca - Dissertação de Mestrado
Capı́tulo 2. Revisão Bibliográfica
Capı́tulo 3
Meta-heurı́stica Colônia de
Formigas
Neste capı́tulo, apresentamos a teoria necessária da meta-heurı́stica para
otimização por colônia de formigas, Ant Colony Optimization - ACO,
e alguns dos algoritmos que a implementam. O escopo deste capı́tulo
é a apresentação da meta-heurı́stica inspirada no comportamento das
formigas, assim também, serão apresentados alguns dos principais autores que aplicaram este método e outros que fizeram a aplicação para
reconfiguração de redes.
3.1
F
Introdução
ENÔMENOS biológicos durante anos vêm sendo matéria de pesquisa no mundo
inteiro de ver a tão grande complexidade que existe e como a ordem e o
equilı́brio prevalece. Este mecanismo tão complexo como é a vida, a reprodução, o
ciclo biológico, o código genético ou metabolismo, a mudança das estações, o tempo
(condições climatológicas), o comportamento das pessoas (o instinto, pensamento
humano), o comportamento instintivo dos animais, a forma de organização de algumas espécies (insetos). Todos estes fenômenos levam muitas variáveis que fazem
difı́ceis e até em alguns dos casos impossı́vel o entendimento delas.
Na ciência temos modelos matemáticos que estão fortemente presentes nas áreas
como a fı́sica, a engenharia. Recentemente pesquisas neste campo na realização da
modelagem matemática desses fenômenos biológicos vêm se realizando. É tão im15
16
Capı́tulo 3. Meta-heurı́stica Colônia de Formigas
portante o estudo destes fenômenos biológicos que existe uma área do conhecimento
que é voltado ao estudo de métodos e técnicas bio-inspiradas.
3.2
Inspiração Biológica
Formigas reais são capazes de encontrar o caminho mais curto (menos difı́cil)
de uma fonte de alimento para o formigueiro. Este comportamento é a grande
inspiração utilizada para o processo de otimização baseada em colônia de formigas.
As formigas, assim como outros insetos sociais, têm uma organização e distribuição
dos indivı́duos em hierarquias, as quais realizam diferentes tipos de trabalhos, porém
estas apresentam uma organização social altamente estruturada. Como resultado
desta organização, colônias de formigas podem realizar tarefas complexas que, em
alguns casos, excedem a capacidade individual de cada um delas (Dorigo e Stutzle,
2004).
Na procura de alimentos, as formigas depositam uma substância quı́mica denominada feromônio, formando uma trilha. Tal trilha, ao ser encontrada por outro
indivı́duo, promove reações comportamentais e é utilizada como meio de comunicação entre elas. Esta comunicação indireta é denominada estigmergia 1 , em que
um indivı́duo da população, alterando um meio próximo a sua localização, altera,
também, todo o ambiente onde ele esteja, provocando, posteriormente, reações de
outros indivı́duos baseadas nesta modificação individual. A auto-organização presente nas colônias de insetos sociais é a idéia principal que é utilizada para coordenar
uma população de formigas artificiais, utilizadas na implementação de algoritmos
baseados em colônia de formigas.
Investigou-se o comportamento das formigas na procura do alimento. No primeiro
experimento, (Dorigo e Stutzle, 2004), da Figura 3.1, o caminho até a fonte de
comida possui duas pontes com o mesmo comprimento. Inicialmente, as formigas
se movem aleatoriamente entre o formigueiro e a fonte de comida, visto que não
há presença do feromônio nos caminhos, estas possuem a mesma probabilidade de
serem escolhidos. Entretanto, de acordo com a flutuação aleatória, um caminho
1
Em 1959, o entomólogo francês Pierre-Paul Grassé, introduziu o conceito de estigmergia para
designar com ela ao processo ou mecanismo pelo qual os insetos sociais como as formigas, os cupins
se comunicam y coordenam em forma indireta, utilizando o meio ambiente.
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 3.2. Inspiração Biológica
17
será escolhido por um número maior de formigas, fazendo com que a quantidade de
feromônio neste caminho seja maior e, até que, com o passar do tempo, a maioria
das formigas escolham uma única ponte.
15 cm
Formigueiro
60o
Comida
Figura 3.1: Experimento ponte de cumprimentos iguais.
Já no segundo experimento, (Dorigo e Stutzle, 2004), da Figura 3.2, as pontes
têm tamanhos diferentes, um caminho é duas vezes maior que o outro. Conforme
esperado, as formigas utilizam o menor caminho entre o formigueiro e a fonte de
comida. As que escolheram o caminho mais curto retornam primeiro da fonte de
comida para o formigueiro. Logo, o caminho mais curto apresentará um maior
nı́vel de feromônio, estimulando mais formigas a seguirem pela mesma trilha. Uma
pequena parte das formigas ainda utiliza o caminho mais longo na busca de alimento.
Este fato pode ser interpretado como exploração do caminho para a procura de novas
fontes de alimento.
Este comportamento coletivo presente nas formigas é chamado de comportamento
autocatalı́tico 2 , onde quanto mais formigas seguem uma trilha, mais atrativa é a
mesma. A probabilidade de um caminho ser escolhido aumenta com o número de
formigas que, previamente, escolheram este mesmo caminho (Dorigo et al., 1996;
Dorigo e Gambardella, 1997; Stutzle e Hoos, 2000; Dorigo e Stutzle, 2004). O
experimento das pontes duplas, (Dorigo e Stutzle, 2004), mostra claramente, que
as colônias têm incorporadas a capacidade de otimização, uma vez que através do
2
Catalisar: Diz-se de alguém ou algo que, com a simples presença, mesmo sem ação direta,
estimula mudanças ou acelera um processo.
17
18
Capı́tulo 3. Meta-heurı́stica Colônia de Formigas
Formigueiro
1
2
Comida
Figura 3.2: Experimento ponte de cumprimentos diferentes.
uso de regras probabilı́sticas, baseada em informações locais, elas podem encontrar
o menor caminho entre dois pontos do ambiente. Pela inspiração do experimento,
é possı́vel desenvolver formigas artificiais, tendo como modelo as formigas reais que
conseguem encontrar o menor caminho entre a fonte de comida e o formigueiro.
3.3
Otimização por Colônia de Formigas
Problemas de otimização combinatória são difı́ceis de resolver, isto é, o seu custo
computacional cresce exponencialmente com o aumento das variáveis de entrada. A
otimização por colônia de formigas Ant Colony Optimization - ACO é uma metaheurı́stica utilizada para a busca da solução de problemas combinatórios. Ela é inspirada no comportamento de formigas na busca de alimentos. Quando uma formiga
precisa decidir para onde ir, ela usa informação do feromônio previamente depositado
por outras formigas que passaram por aquele local (Dorigo e Stutzle, 2004).
3.3.1
Colônia de formigas aplicado ao problema do caixeiro
viajante (Traveling salesman problem - TSP )
O caso, por exemplo, do problema do caixeiro viajante Traveling Salesman Problem - TSP, consiste em encontrar o menor caminho para percorrer um conjunto
de cidades que estão completamente conectadas entre si, isto é, para cada par de
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 3.3. Otimização por Colônia de Formigas
19
cidades, há uma estrada que as liga. O problema consiste, então, em encontrar
o menor caminho para percorrer todas as cidades uma única vez. O conjunto de
todos os caminhos possı́veis define o espaço de busca para este problema. Para
conjuntos de poucas cidades, até cinco ou seis, podemos testar todas as possibilidades
para encontrar o menor caminho. Mas o problema se torna computacionalmente
intratável para conjuntos maiores de cidades. Tal fato despertou a necessidade de se
elaborar estratégias computacionalmente eficientes, mas que encontrassem soluções
ótimas ou próximas delas, para esse tipo de problema. Essa é a idéia principal
por trás das meta-heurı́sticas. São estratégias para explorar o espaço de busca de
maneira eficiente, encontrando soluções ótimas, próximas da melhor solução.
5
4
3
28
27
29
1
6
26
30
7
24
2
8
25
9
10
22
12
13
23
11
15
14
21
18
19
16
17
20
Figura 3.3: Resultado obtido para o problema do caixeiro viajante Traveling Salesman Problem - TSP para 30 cidades aplicando sistema de formigas Ant System AS (Dorigo et al., 1991).
O método de otimização baseado no comportamento de colônias de formigas, Ant
Colony Optimization - ACO (Dorigo et al., 1991; Dorigo et al., 1996; Dorigo e Gambardella, 1997; Stutzle e Hoos, 2000; Dorigo e Stutzle, 2004),é constituı́do por um
conjunto de agentes simples, que realizam suas tarefas de forma cooperativa, com
o objetivo de encontrar boas soluções para problemas de otimização discretos complexos. As caracterı́sticas apresentadas pelas formigas reais podem ser facilmente
19
20
Capı́tulo 3. Meta-heurı́stica Colônia de Formigas
estendidas a agentes artificiais por meio de:
1. Definição de variáveis de estado apropriadas aos estados do problema.
2. Acesso local aos valores destas variáveis pelos agentes artificiais.
Os agentes artificiais irão simular a construção da trilha de feromônio realizada
pelas formigas através da modificação das variáveis associadas aos estados do problema durante a busca de soluções. As formigas artificiais apresentam algumas
caracterı́sticas semelhantes às formigas reais, adicionadas de algumas capacidades
necessárias à resolução de problemas de otimização combinatória.
3.4
3.4.1
Colônia de Formigas
Ant System - AS
O sistema de formigas, Ant System - AS, primeiro algoritmo baseado no comportamento da colônia de formiga foi proposto pela primeira vez no inicio da década
dos 90 (Dorigo et al., 1991). A metodologia chamada Ant Sysem - AS, (Dorigo
et al., 1996) foi aplicada para resolver o problema clássico do caixeiro viajante,
Traveling Salesman Problem - TSP. Três versões do algoritmo AS foram propostos,
(Dorigo et al., 1991): Ant-density, Ant-quantity, Ant-cycle. A diferença destas
versões do algoritmo fica apenas na forma de atualização do feromônio.
O problema clássico do caixeiro viajante (TSP), consiste em, por exemplo, dado
um conjunto de cidades e dada também a distância entre cada uma delas, determinar
a menor rota para o caixeiro viajante que contemple todas as cidades, passando
por cada cidade uma única vez e voltando ao ponto de partida. O TSP pode ser
representado por um grafo G(C, N), onde C e conjunto das cidades e N representa
as conexões (estrada), entre as cidades. A distância entre a cidade i e a cidade
j assume o valor d(i, j). De forma tal que, o algoritmo e inicializado com uma
população de formigas. Cada formiga k escolhe, aleatoriamente, uma cidade que
será o ponto de partida. Cada agente pertencente à colônia constrói uma solução.
A escolha da próxima cidade a ser visitada é baseada na concentração do feromônio
τ (i, j) e na informação heurı́stica η(i, j) . Isso é feito por meio de uma regra de
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 3.4. Colônia de Formigas
21
transição, equação (3.1), que fornece a probabilidade de cada formiga escolher o
caminho (i, j) ainda não visitado.
P robk (i, j) =











[τ(i,j) ]α [η(i,j) ]β
P
[τ(i,v) ]α [η(i,v) ]β
se j ∈ Jk (i);
v∈Jk (i)
0
(3.1)
Caso contrário,
sendo P robk é a probabilidade de que a formiga k escolha o caminho (i, j), τ(i,j)
representa a quantidade de feromônio no caminho (i, j), η(i,j) é uma informação
previa (heurı́stica) do problema, um ı́ndice de atratividade de escolha pelo caminho
(i, j), Jk é conjuntos das cidades ainda não visitadas pela formiga k, α e β são os
parâmetros de controle que determinam o peso relativo da influência da concentração
de feromônio ou da informação heurı́stica do problema, dij é a distância entre as
cidades (i, j).
A informação heurı́stica pode existir ou não. Isso depende do problema em estudo.
Para este caso do problema do caixeiro viajante este valor é representado por:
η(i,j) =
1
dij
(3.2)
Como o problema é de minimização, quanto menor a distância d(i, j) , maior deverá ser a quantidade de feromônio associada a este caminho. Ou seja, de maneira
geral, os melhores caminhos terão maior valor de feromônio associado. Os parâmetros
α e β constituem uma informação importante no processo de busca. Se α = 0 as
cidades mais próximas tem maior chance de serem selecionadas, já que a probabilidade de escolha é em função da informação heurı́stica η(i, j) . Caso β = 0 somente
as informações baseadas no feromônio são determinantes na escolha, podendo levar
o algoritmo a uma estagnação em uma solução sub ótima. Dorigo e Stuzle (2004)
indicam os valores apropriados dos parâmetros para cada versão do AS. Posteriormente, após todas as formigas completarem o ciclo, as trilhas de feromônio são
atualizadas pelo acréscimo e evaporação do fenômeno, equação (3.3) (Dorigo e Stutzle, 2004). A evaporação é representada pelo coeficiente ρ, que pode variar entre
zero e o valor unitário.
21
22
Capı́tulo 3. Meta-heurı́stica Colônia de Formigas
τ (i, j) = (1 − ρ).τ (i, j) + ∆τ (i, j)
(3.3)
Sendo ∆τ (i, j), o depósito de feromônio de todas as formigas no caminho (i, j),
que se expressa do seguinte modo:
∆τ (i, j) =
m
X
∆τk (i, j)
(3.4)
k=1

Q


se (i, j) ∈ a rota da formiga k ;
Lk
∆τk (i, j) =


0
Caso contrário,
(3.5)
Sendo, m o número de formigas, Q constante de peso para o depósito de feromônio,
Lk Comprimento da rota da k-ésima formiga.
A equação (3.5) representa a quantidade de feromônio depositado pela formiga
k nos caminhos que ela percorreu. Desta forma, quanto mais formigas utilizarem
um arco pertencente a um menor caminho, maior será a quantidade de feromônio
depositado neste arco, fazendo com que este caminho tenha mais chance de ser
escolhido por outras formigas.
Os algoritmos ant-quantity e anty-density diferem do ant-cycle apresentado acima.
Apenas na atualização do depósito de feromônio, nas versões ant-quantity e antydensity, a atualização do feromônio é feito após a formiga se mover entre as cidades.
Na versão ant-cycle, a trilha de feromônio é atualizada somente após todas as formigas completarem o ciclo, ou seja, após todas as cidades terem sido visitadas por elas.
Na versão ant-quantity, o depósito de feromônio tem a seguinte expressão:
∆τk (i, j) =





W
se a k-ésima formiga caminha de i para j ;
d(i, j)
0
(3.6)
Caso contrário,
onde W é um valor constante.
Na versão ant-density, é depositado um valor constante D para a formiga k,
quando ela caminha da cidade i para a cidade j, equação (3.7) :
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 3.4. Colônia de Formigas
∆τk (i, j) =
23

 D se a formiga k vai de i para j ;
 0
(3.7)
Caso contrário,
Comparando o ant-cycle com as versões ant-quantity e ant-density, aquele primeiro
apresentou um resultado superior aos demais, pois o ant-cycle usa informação global
na atualização do feromônio, enquanto os demais modelos utilizam informações locais que não indicam uma medida do resultado final (Dorigo et al., 1991; Dorigo et
al., 1996).
3.4.2
Elitist Ant System - EAS
Na versão Elitist Ant System - EAS, proposta por Dorigo et al., (1991), Dorigo
et al., (1996) e Dorigo e Stutzle, (2004), a principal modificação é o reforço do
melhor caminho desde o inı́cio do processo iterativo. Para isso, a melhor solução,
denominada T bs (best-so-far tour ), é acrescentada à equação (3.3) como um depósito
adicional de feromônio, conforme equações (3.8) e (3.9).
τ (i, j) = (1 − ρ) ∗ τ (i, j) + ∆τ (i, j) + e ∗ ∆τ bs (i, j)
(3.8)
onde ∆τ (i, j) é definido como na equação (4.6) e:

1


se (i, j) ∈ T bs ;
bs
bs
C
∆τ (i, j) =


0
Caso contrário,
(3.9)
onde e é o parâmetro que define o peso ao T bs , C bs é comprimento do menor
(melhor) caminho encontrado.
Dorigo et al., (1996), sugerem um valor apropriado para o parâmetro e.
3.4.3
Ant Colony System - ACS
A versão proposta por Dorigo e Gambardella, (1997), a Ant Colony System - ACS,
é baseada na versão Ant-Q (Gambardella e Dorigo, 1995) e difere da versão AS em
três pontos: (i) explora a experiência acumulada pelas formigas; (ii) a atualização
do depósito e da evaporação é realizada somente para a solução que apresenta o
23
24
Capı́tulo 3. Meta-heurı́stica Colônia de Formigas
menor caminho; (iii) a cada iteração uma quantia do feromônio do caminho (i, j)
é removido para aumentar a exploração de novos caminhos, evitando a estagnação
prematura. Sendo assim, a probabilidade da formiga k se mover da cidade i para a
cidade j é dada pela equação (3.10):
Pk =

 argmaxj∈Jk (i) [τ (i, j)].[η(i, j)]β se q ≤ q0
J

(3.10)
Caso contrário,
sendo, q um número aleatório dentro do intervalo [0,1], q0 é o parâmetro com
valor: 0 ≤ q0 ≤ 1; Jk é um conjunto das cidades ainda não visitadas pela formiga k,
J representa a regra de probabilidade conforme equação (3.1) com α = 1
A atualização global ocorre após o fim de cada iteração, somente para a solução
que apresentar o menor caminho, e é atualizada do seguinte modo:
τ (i, j) = (1 − ρ).τ (i, j) + ∆τ best (i, j),
(3.11)
sendo, ρ o parâmetro de decaimento do feromônio, variando entre zero e um, ∆τ best
representa o depósito de feromônio para o melhor caminho, Jk é o conjuntos das
cidades ainda não visitadas pela formiga k, J é a regra de probabilidade conforme
equação (3.1) com α = 1.
Já a atualização local, é realizada logo após as formigas atravessarem o arco (i, j)
durante a construção do caminho, e de acordo com a equação (3.12):
τ (i, j) = (1 − ξ) ∗ τ (i, j) + ξτ0 ,
(3.12)
onde, ξ o parâmetro de decaimento do feromônio, variando entre zero e um, τ0 é o
parâmetro do valor inicial da trilha de feromônio, Jk o conjunto das cidades ainda
não visitadas pela formiga k.
3.4.4
MAX-MIN Ant System - MMAS
Observando a convergência precoce do sistema de formigas, Ant System - AS,
Stutzle e Hoos, (2000), os autores propuseram o MAX-MIN Ant System - MMAS.
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 3.5. Aplicação do Algoritmo Colônia de Formigas
25
O MMAS, introduz quatro modificações no AS : (i) faz o reforço do melhor caminho encontrado, somente da formiga k que possui a melhor solução. Essa escolha
pode ser feita pela melhor solução encontrada na iteração corrente ib (iteration-best
- ib) ou pela melhor solução global encontrada durante todo o processo iterativo
bs (best-so far - bs). A solução só será atualizada caso seja encontrada uma melhor solução nas iterações seguintes; (ii) a fim de evitar a estagnação do algoritmo,
causado pelo aumento de feromônio nas trilhas de menor caminho, são definidos
os limites mı́nimos e máximos para o depósito de feromônio [τmin , τmax ] nas trilhas;
(iii) as trilhas de feromônio são inicializadas com um alto valor de feromônio, τmax ,
que juntamente com um pequeno coeficiente de evaporação, favorece a exploração
de novos caminhos já no inicio do processo iterativo; (iv) as trilhas de feromônio são
re-inicializadas assim que ocorrer a estagnação em uma solução.
A etapa de construção é praticamente idêntica a do Ant System-AS, usando a
mesma fórmula para calcular a probabilidade (3.1). As modificações mais substanciais dizem respeito à taxa de atualização do feromônio e a sua limitação a certos
valores máximo e mı́nimo. Este processo é mostrado com maior detalhe no capı́tulo
4.
3.5
3.5.1
Aplicação do Algoritmo Colônia de Formigas
Problema de Reconfiguração de Sistemas de Distribuição
de Energia Elétrica
Dado que o problema de reconfiguração de sistemas de energia elétrica é combinatória e não linear, é preciso a aplicação de uma ferramenta que ajude a encontrar
uma solução para este problema. Meta-heurı́sticas foram propostas para encontrar
a solução do problema garantindo, que as restrições impostas fossem satisfeitas. A
reconfiguração de sistemas de distribuição de energia elétrica consiste basicamente
na abertura e fechamento de chaves de interconexão para encontrar uma topologia
que apresente o menor valor de perdas totais de potência ativa. O problema de
reconfiguração de redes esta intimamente relacionada ao número de chaves envolvidas na busca da melhor configuração, cujo problema torna-se mais complicado se
o número de chaves aumenta, devido a que o número de combinações feitas para
25
26
Capı́tulo 3. Meta-heurı́stica Colônia de Formigas
achar a melhor configuração aumenta exponencialmente.
No método por colônia de formigas, um conjunto de formigas artificiais cooperam
entre se a fim de realizar uma busca entre todas as configurações possı́veis e achem
uma que apresente o menor valor de perdas do sistema. Na literatura foi feita a
aplicação do algoritmo por colônia de formigas nas versões: Ant System - ACO, Ant
Colony System - ACS, entre outras.
Pereira et al., (2006) utilizam o método, Otimização por Colônia de Formigas
(Ant Colony Optimization - ACO) o método foi proposto para redução das perdas
de potência ativa, satisfazendo as restrições de limites de tensão nas barras, limites
de corrente no trechos e que a configuração encontrada seja sempre radial (Pereira
et al., 2006). O algoritmo foi aplicado num sistemas de distribuição ideal de 5 barras
a fim de verificar a eficiência do algoritmo.
Zhijiam et al., (2008) apresentam um algoritmo baseado num sistemas colônia de
formigas Ant Colony System Algorithm - ACSA para a reconfiguração sistemas de
distribuição com o objetivo de reduzir as perdas de potência ativas em condições
normais de operação. Para atualização do feromônio é utilizada uma regra de Atualização global do feromônio, segundo a qual só nas ligações que compõem a melhor
solução é que há aumento de feromônio (Zhijiam et al., 2008). No algoritmo proposto ales aplicam uma variação do α, β e ρ e fazem uma comparação das soluções
encontradas. O algoritmo foi aplicado num sistemas de distribuição de 69 barras.
Abdelaziz et al., (2012), apresentam a otimização por colônia de formigas Ant
Colony Optimization - ACO, e um algoritmo implementado no Hyper-cube - HC,
uma variação do algoritmo colônia de formigas, para resolver o problema de reconfiguração de sistemas de distribuição a fim de minimizar as perdas de potência da
rede. A conclusão do trabalho é que: em contraste com as formas usuais de aplicação
do algoritmo ACO, a estrutura do HC, limita os valores de feromônio por introdução
de alterações nas regras de atualização do feromônio resultando um algoritmo mais
robusto e fácil de implementar que na versão do ACO (Abdelaziz et al., 2012). O
problema de otimização foi formulado tendo em conta as restrições operacionais dos
sistemas de distribuição, limites de tensão nas barras, limites de corrente nos trechos e a topologia encontrada seja radial. Este algoritmo também utiliza regras de
Atualização local e Atualização global do feromônio. O algoritmo foi aplicado a três
sistemas de distribuição de 33, 69 e de 119 barras e seus resultados foram comparaHuilman Sanca Sanca - Dissertação de Mestrado
Seção 3.6. Conclusão do Capı́tulo
27
dos com outros dois métodos sendo eles: Têmpera simulada (Simulated Annealing SA), Nuvem de partı́culas (Particle Swarm - PS ), Busca Tabu (Tabu Search - TS ),
tendo sido encontrado os mesmos resultados.
3.6
Conclusão do Capı́tulo
Neste Capı́tulo, foram apresentadas as informações necessárias, básicas do processo de otimização bio-inspirado em colônia de formigas, tais como: inspiração
biológica, modelagem, formulação, algoritmo e as variações entre as principais modelagens existentes. Desta forma, pode-se verificar que o processo de busca, tem como
ponto forte o fato de que as informações de todos os indivı́duos da colônia são utilizadas na obtenção da solução ótima, isto é o que origina a chamada inteligência
coletiva. Além disso, foram citas algumas aplicações do ACO que podem ser encontradas na literatura. Apresentaram também alguns trabalhos que utilizaram o
método ACO, para reconfiguração de sistemas de distribuição de energia elétrica,
que na maioria das vezes utilizaram o algoritmo ACS, e em outros casos, alguns
autores aplicaram, para melhora do desempenho, modificações no algoritmo base de
sistema de formigas (Ant System - AS ).
27
28
Capı́tulo 3. Meta-heurı́stica Colônia de Formigas
Huilman Sanca Sanca - Dissertação de Mestrado
Capı́tulo 4
Metodologia Proposta
Neste capı́tulo apresentamos a meta-heurı́stica MAX-MIN Ant System
- MMA uma variante do algoritmo colônia de formigas. O algoritmo
foi implementado para resolver o problema clássico do caixeiro viajante,
Traveling Salesman Problem - TSP, esta meta-heurı́stica foi estudada
por (Stutzle e Hoos, 1996; Stutzle e Hoos, 2000; Dorigo e Stutzle, 2004),
O principal objetivo deste capitulo é aplicar o MMAS ao problema de reconfiguração de sistemas de distribuição de energia elétrica para redução
das perdas de potência ativa do sistema.
4.1
G
Introdução
RANDE parte dos sistemas de distribuição de energia elétrica têm uma configuração radial com o fim de facilitar sua expansão. Cada alimentador têm
uma mistura diferente de carga diária do tipo industrial, comercial e residencial.
Este tipo de carga variável fazem com que picos de carga nos alimentadores se apresentem em diferentes momentos. A sobrecarga do sistema de distribuição pode
causar problemas na distribuição a partir do desligamento de ramos por causa do
disparo dos dispositivos de proteção.
O processo de reconfiguração é feito através da operação de chaves que estão
normalmente abertas e chaves que estão normalmente fechadas (Abdelaziz et al.,
2012). Estes dos tipos de chaves são projetados para proteção e gerenciamento
das redes. No fim a reconfiguração de sistemas de distribuição é o processo de
29
30
Capı́tulo 4. Metodologia Proposta
mudança de uma topologia para outra em condições normais de operação, para
transferir cargas de alimentadores com carga pesada para os relativamente menos
sobrecarregados. Esta transferência é eficaz não só em termos de equilı́brio das
cargas, mas também para a melhoria do perfil de tensão ao longo do sistema e com
isso reduzir as perdas de potência ativa decorrentes da operação no sistema.
4.2
Formulação do problema
Esta formulação do problema de reconfiguração de redes é um tı́pico problema
de otimização não linear combinatória de variáveis inteiras e reais e que pode ser
expresso do seguinte modo:
Minimizarf (x) = PT,P erdas =
NX
B −1
Pperdas (i, i + 1)
(4.1)
i=1
Sujeito as restrições:
1. de fluxo de carga;
2. limites de corrente nos trechos:
|Ij | ≤ Ij,max ; ∀j, j ∈ NT
(4.2)
3. configuração radial da rede.
Onde PT,perdas é a perda de potência ativa total do sistema, |Ii | e Ii,max são a
amplitude da corrente e o limite máximo de corrente em cada trecho i, respectiva-
mente, NB é o número de barras do sistema e NT é o conjunto de trechos de linha
do sistema.
O problema de otimização com restrições expresso na equação (4.1), pode ser
convertido num problema de otimização irrestrito cuja função objetivo incorpore a
restrição de corrente máxima nos trechos (Lin et al., 2000; Pereira et al., 2006).
Minimizef (x) =
NX
B −1
Pperdas (i, i + 1) +
i=1
Huilman Sanca Sanca - Dissertação de Mestrado
NT
X
j=1
λI (Ij − Ij,max )2
(4.3)
Seção 4.3. Algoritmo MAX-MIN Ant System - MMAS
31
sendo λI um fator de penalidade com respeito à corrente admissı́vel no trecho.
A primeira restrição é intrı́nseca, em vista de que o valor das perdas totais de
potência ativa é calculado mediante um método computacional que tem por base
as equações de fluxo de potência. Aproveitando-se da terceira restrição que indica
uma configuração radial da rede no final do processo, emprega-se para o cálculo
de fluxo de carga o método da soma de potência - MSP (Haque, 1996), por ser de
eficiência computacional reconhecida. O cálculo de fluxo de carga pelo método MSP,
é apresentado no capı́tulo 5.
4.3
4.3.1
Algoritmo MAX-MIN Ant System - MMAS
O Paradigma do Algoritmo MAX-MIN Ant System
Utilizada para a Reconfiguração de Sistemas de Distribuição de Energia Elétrica
O algoritmo MMAS é uma das variações do algoritmo colônia de formigas, Ant
Colony Optimization - ACO, que é uma meta-heurı́stica inspirada em formigas reais
(Dorigo et al., 1996; Stutzle e Hoos, 1996; Dorigo e Gambardella, 1997; Stutzle e
Hoos, 2000; Dorigo e Stutzle, 2004; Dorigo et al., 2006).
Na procura por alimento as formigas inicialmente se movimentam sem direção
preferencial. Mais tarde, as formigas que escolheram o caminho mais curto entre
o formigueiro e a fonte de alimento completarão as expedições mais rapidamente
reforçando a trilha de feromônio, isto fará que mais formigas escolham o menor
caminho devido à maior concentração de feromônio. No final, a maioria das formigas
irá escolher o menor caminho, devido ao aumento constante do feromônio.
Na Figura 4.1(a), as formigas inicialmente exploram a área circundante do formigueiro
de forma aleatória em busca de alimento. Assim que uma formiga encontra uma
fonte de alimento, enquanto caminha de volta para o formigueiro, a formiga deposita
um rastro de feromônio no chão. As trilhas de feromônio depositados irá orientar
outras formigas para a fonte de alimento de modo que a maior parte das formigas
encontrão esse caminho como mostrado na Figura 4.1(b). Este modo de operação
das formigas fará que outras formigas circundantes escolham esse caminho, devido
a que ficara com maior concentração de feromônio. Este comportamento social e
31
32
Capı́tulo 4. Metodologia Proposta
Alimento
Alimento
Obstáculo
Obstáculo
Formigueiro
Formigueiro
(a)
(b)
Figura 4.1: Exemplo de uma colônia de formigas real explicando o comportamento
delas na procura de alimento.
cooperativo das formigas mostra o paradigma fundamental do algoritmo de busca
por colônia de formigas.
4.3.2
Regra de Transição de Estado
Na fase de construção da solução do problema, no começo do algoritmo, todos os
trechos do sistema de distribuição têm a mesma quantidade de feromônio. Então,
a formiga parte da subestação e escolhe a seguinte barra a ser visitada com uma
probabilidade que é uma função da resistência e da quantidade de feromônio presente
no trecho que liga a barra onde esta a formiga com as outras barras adjacentes
ainda não visitadas, e decidirá para onde vai continuar caminhando realizando uma
seleção aleatória. As barras com maior probabilidade terão mais chances de serem
escolhidas. Para não permitir passos inválidos, as formigas artificiais são dotadas de
uma memória das informações dos trechos já visitados. Assim, ao mesmo tempo em
que a formiga constrói a configuração radial da redes, ela é forçada a não visitar um
mesmo trecho de rede duas vezes, até encontrar uma configuração radial completa.
A probabilidade para que um dos trechos adjacentes seja selecionado pela formiga,
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 4.3. Algoritmo MAX-MIN Ant System - MMAS
33
é dada pela equação (4.4):
P rob(i,j) =









[τ ]α [η(i,j) ]β
P (i,j)
[τ(i,m) ]α [η(i,m) ]β
se ∀j ∈ JK(i) ;
m∈JK(i)
(4.4)
0 se ∀j ∈
/ JK(i) ,
Sendo, P rob é a probabilidade que um trecho (i, j) seja escolhido; τ(i,j) é a
quantidade de feromônio na ligação escolhida (i, j); η(i,j) é uma informação prévia
(heurı́stica) do problema, um ı́ndice de atratividade de escolha pelo caminho (i, j),
Jk é o conjunto de barras ainda não visitadas pela formiga k; α e β são os pesos do
grau de atratividade, τ , e a visibilidade do feromônio, η respectivamente, JK(i) é o
conjunto das ligações adjacentes que poderão ser visitadas pela formiga K que se
encontra no nó i.
Observando a convergência precoce do algoritmo colônia de formigas - ACO, em
(Stutzle e Hoos, 1996; Stutzle e Hoos, 2000), os autores propuseram o MAX-MIN
Ant System - MMAS. As modificações mais substanciais dizem respeito à taxa de
atualização do feromônio e a sua limitação a certos valores máximo e mı́nimo do
feromônio.
4.3.3
Regra de Atualização do Feromônio
Como no algoritmo ACO, a atualização do feromônio é feita apenas quando termina a fase de construção, porém, diferentemente da ACO, a atualização no MMAS
é feita apenas pela melhor formiga (na nossa proposta isto corresponde ao conjunto de formigas que gerou a melhor configuração da iteração). A atualização do
feromônio é feita a partir da equação (4.5)
Imediatamente após a determinação de uma configuração radial é calculada a
perda de potência ativa do sistema e o nı́vel de feromônio é atualizado, apenas nos
trechos que fazem parte da melhor solução, da seguinte forma:
τ(i,j) = (1 − ρ)τ(i,j) + △τ melhor
(4.5)
Onde:
33
34
Capı́tulo 4. Metodologia Proposta
△τ melhor =
1
Fmelhor
(4.6)
Sendo Fmelhor o valor da melhor solução encontrada da função objetivo até o momento (melhor solução global) ou a melhor solução da iteração. Neste trabalho é
utilizado a melhor solução de um conjunto de soluções, porque assim ocorre menos
risco de convergência prematura, do que usando a melhor solução global. No problema de reconfiguração de redes Fmelhor representa as perdas de potência ativa
da configuração encontrada. Como o feromônio é uma substância volátil essa propriedade evita que soluções antigas sejam esquecidas, (1 − ρ) é a taxa de evaporação
do feromônio, sendo ρ um valor entre [0, 1].
De acordo com Stuzle e Hoos a utilização da melhor solução de uma iteração
aumenta o efeito de exploração das melhores soluções durante o processo de busca
(Stutzle e Hoos, 1996; Stutzle e Hoos, 2000). Ao mesmo tempo, contribui para o
efeito de intensificação do processo utilizando sempre as melhores soluções en cada
iteração para a atualização do feromônio.
4.3.4
Limites de Feromônio
Outra diferença, comparando o MMAS e ACO, é que no MMAS, existem limites superior e inferior para o nı́vel de feromônio. Ao realizar uma atualização do
feromônio (aumento e evaporação) num ramo, o seu valor não pode ultrapassar τmax ,
nem ser inferior a τmin .
No MMAS, a proposta de impor limites superior e inferior é para evitar que o
feromônio depositado fique muito grande. Esta limitação é entre um valor máximo
e um mı́nimo de τ , sendo assim, após cada iteração, se τi,j > τmax , então τi,j = τmax ,
se τi,j < τmin , então τi,j = τmin , além disso τmin > 0, se ηi,j < ∞, para todas as
componentes da solução. Adicionalmente propõe-se a reinicialização do feromônio,
este passo será feito quando um número pre-definido de iterações é atingido sem ser
encontrada uma solução melhor (estagnação do algoritmo) (Stutzle e Hoos, 2000).
Pode-se dizer que esta proposta de impor limites ao feromônio, tem um efeito de
intensificação no processo de busca da melhor solução (para encontrar um maior
número de possibilidades). A dificuldade é determinar quais são os valores apropriados para τmin e τmax . τmax é definido pela equação (4.7) (Stutzle e Hoos, 1996):
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 4.3. Algoritmo MAX-MIN Ant System - MMAS
τmax =
1
∗
ρ.Fmelhor
35
(4.7)
Stuzle e Hoos (2000) também propõem inicializar o algoritmo fazendo τ0 = τmax ,
para obter uma intensa exploração das soluções no espaço de busca (Stutzle e Hoos,
2000).
Enquanto ao valor de τmin , não há um completo acordo sobre como pode ser
determinado. Dorigo et al., (1996) diz que este valor de τmin é determina empiricamente (Dorigo et al., 1996), porém existe uma proposta analı́tica para determinar
este valor, equação (4.8) (Stutzle e Hoos, 1996).
τmin =
τmax .(1 − Pdec )
k.Pdec
(4.8)
Onde k é a quantidade média de barras adjacentes que a formiga pode escolher
em qualquer ponto de decisão, e Pdec determinado pela equação (4.9):
Pdec =
p
n−1
Pmelhor
(4.9)
Onde Pmelhor é a probabilidade de uma formiga construir o melhor caminho até
agora, e n é o número de passos no caminho (número de barras).
Inicialmente todos os trechos têm a mesma quantidade de feromônio τ0 = τmax ,
todas as barras-fontes estão ligados, enquanto as barras de carga estão todos desligados, de modo que nenhuma ligação está ativada. Sendo, barra ligada é aquela
onde está a formiga no momento, em outro caso a barra fica desligada (barra que a
formiga ainda pode visitar). Ligação ativada é aquela ligação que já foi percorrida
e ligação ativável é aquela ligação adjacente por onde a formiga pode continuar o
percurso.
As formigas partem simultaneamente de forma aleatória das barras ligadas respeitando as seguintes regras:
1. As formigas se deslocam exclusivamente por ligações ativáveis ou adjacentes
a ela;
2. Quando uma formiga chega a uma barra desligada da ligação ativável que
tenha percorrido:
35
36
Capı́tulo 4. Metodologia Proposta
• esta barra torna-se ligada e a ligação ativada;
• surge outra formiga para ocupar a barra originalmente ligada deixado por
ela;
3. O percurso de uma formiga se completa quando ela não puder mais seguir por
ligações ativáveis;
4. A expedição termina quando nenhuma formiga tiver mais mobilidade, ou seja,
quando não houver nenhuma ligação ativável.
No final do processo de uma expedição sempre se terá determinado uma configuração radial do sistema. O número de formigas por expedição é variável. Ela
começa igual ao número de barras-fontes. As formigas vão surgindo aleatoriamente
de barras ligadas e se movimentam por ligações ativáveis ou adjacentes enquanto
puderem. De acordo com as regras estabelecidas acima pontos 1, 2, 3 e 4. Uma vez
que é encontrada uma melhor solução da configuração radial do sistema são calculadas as perdas dela e atualiza-se o nı́vel de formônio para depois ser comparada
com os nı́veis de feromônio τmin , τmax , se τi,j < τmin ou τi,j > τmax os valores de τi,j
serão τij = τmin ou τij = τmax respectivamente.
4.4
Exemplo de Busca das configurações radiais
A Figura 4.2 (Pereira et al., 2006), representa um sistemas de distribuição fictı́cio
utilizado para explicar melhor o processo de busca das configurações radiais do
sistema.
As resistência (R) em p.u., utilizada para os trechos são: (trecho 1-2=12), então
R12 = 0, 66; R13 = 0, 16; R23 = 0, 03; R24 = 0, 51; R34 = 0, 05; R35 = 0, 27;
R45 = 0, 33; e α = 1, β = 2, τ0 = 1, η será a inversa da resistência 1/R, então temos:
η12 = 1, 52; η13 = 6, 25; η23 = 33, 33; η24 = 1, 96; η34 = 20; η35 = 3, 7; η45 = 3, 03.
Tendo os valores necessários a construção da solução começa alocando uma formiga
nas barras subestação (barra 1), enquanto nenhuma ligação está ativada como
mostrado na Figura 4.3(a), as barras subestação estão ligados e tem um valor de
um 1 e as barras de carga que ainda não foram visitadas por nenhuma formiga tem
valor de zero 0 como mostrado na Figura 4.3(b). É colocado uma formiga na barras
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 4.4. Exemplo de Busca das configurações radiais
2
4
3
5
37
1
Figura 4.2: Sistema fictı́cio de 5 barras, rede malhada.
1, nesse momento a formiga tem duas possibilidades para se deslocar, para a barra 2
pelo trecho 1-2 ou para a barra 3 pelo trecho 1-3 como apresentado na Figura 4.3(b),
para determinar para onde a formiga fará o seu próximo movimento é calculado as
probabilidades para os trechos candidatos (trecho 1-2 ou 12 e 1-3 ou 13) mediante
e equação (4.4).
2
4
1
1
1
3
5
2
4
0
0
0
0
3
(a)
5
(b)
Figura 4.3: Sistema fictı́cio de 5 barras na inicialização do processo, (a) sistema com
os trechos não ativados, (b) trechos adjacentes (ativáveis) por onde a formiga pode
se movimentar.
β
P rob1−2 =
α
τ12
.η12
β
β
=
β
=
α .η
α
τ12
12 + τ13 .η13
β
P rob1−3 =
α
τ13
.η13
β
α .η
α
τ12
12 + τ13 .η13
11 ∗ 1, 522
11 ∗ 1, 522 + 11 ∗ 6, 252
11 ∗ 6, 252
11 ∗ 1, 522 + 11 ∗ 6, 252
= 0, 0558
= 0, 9441
Logo após do cálculo das probabilidades, a seguinte barras a ser visitada pela
formiga será determinada mediante um sorteio aleatório (roleta). Supondo que a
37
38
Capı́tulo 4. Metodologia Proposta
barra 3 seja a sorteada, Figura 4.4, então o trecho 1 − 3 será percorrido e a barra 3
será ligada (um) como mostrado na Figura 4.5
...
1-2 1-2 1-2 1-2 1-2 1-3 1-3 1-3 1-3 1-3
6%
1-3 1-3
94%
Figura 4.4: Roleta aleatória para escolha entre os trechos 1-2 e 1-3.
1
1
2
4
0
0
1
0
3
5
Figura 4.5: Sistema fictı́cio de 5 barras, deslocamento do agente desde a barra 1 até
a barra 3.
Agora, têm-se que as barras 2, 4 e 5 podem ser escolhidas e será novamente
calculada as probabilidades que tem cada trecho.
P rob1−2 =
β
α
τ12
.η12
11 ∗ 1, 522
= 0, 001513
=
β
β
β
β
1 ∗ 1, 522 + 11 ∗ 33, 332 + 11 ∗ 202 + 11 ∗ 3, 72
α
α
α
α
1
τ12 .η12 + τ32 .η32 + τ34 .η34 + τ35 .η35
P rob3−2 =
β
α
τ32
.η32
11 ∗ 33, 332
=
= 0, 7276
β
β
β
β
1
2
1
α
α
α
α
1 ∗ 1, 52 + 1 ∗ 33, 332 + 11 ∗ 202 + 11 ∗ 3, 72
τ12 .η12 + τ32 .η32 + τ34 .η34 + τ35 .η35
P rob3−4 =
β
α
τ34
.η34
11 ∗ 202
=
= 0, 2619
β
β
β
β
1 ∗ 1, 522 + 11 ∗ 33, 332 + 11 ∗ 202 + 11 ∗ 3, 72
α
α
α
α
1
τ12 .η12 + τ32 .η32 + τ34 .η34 + τ35 .η35
P rob3−5 =
β
α
τ35
.η35
11 ∗ 3, 72
=
= 0, 00854
β
β
β
β
1 ∗ 1, 522 + 11 ∗ 33, 332 + 11 ∗ 202 + 11 ∗ 3, 72
α
α
α
α
1
τ12 .η12 + τ32 .η32 + τ34 .η34 + τ35 .η35
Logo após do cálculo das probabilidades, a seguinte barras a ser visitada pela
formiga será determinada mediante um sorteio aleatório (roleta), Figura 4.6.
Supondo que a barra 4 seja a sorteada, então o trecho 3 − 4 será percorrido e a
barra 4 será ligada (um) como mostrado na Figura 4.7
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 4.4. Exemplo de Busca das configurações radiais
...
1-2 3-2 3-2 3-2
0,15%
...
3-2 3-2 3-4 3-4 3-4 3-4 3-4
26%
39
73%
3-4 3-4 3-5
0,85%
Figura 4.6: Roleta aleatória para escolha entre os trechos 1-2, 3-2, 3-4 e 3-5.
1
1
2
4
0
1
1
0
3
5
Figura 4.7: Sistema fictı́cio de 5 barras, deslocamento do agente desde a barra 3 até
a barra 4.
Agora, têm-se que as barras 2 e 5 podem ser escolhidas e será novamente calculada
as probabilidades que tem cada trecho.
β
P rob1−2 =
α
τ12
.η12
β
β
β
β
β
β
β
=
β
β
=
α .η
α
α
α
α
τ12
12 + τ32 .η32 + τ35 .η35 + τ42 .η42 + τ45 .η45
β
P rob3−2 =
α
τ32
.η32
β
α .η
α
α
α
α
τ12
12 + τ32 .η32 + τ35 .η35 + τ42 .η42 + τ45 .η45
β
P rob3−5 =
α
τ35
.η35
β
β
β
β
β
α .η
α
α
α
α
τ12
12 + τ32 .η32 + τ35 .η35 + τ42 .η42 + τ45 .η45
=
β
P rob4−2 =
α .η
τ42
42
β
β
β
β
β
β
β
=
β
β
=
α .η
α
α
α
α
τ12
12 + τ32 .η32 + τ35 .η35 + τ42 .η42 + τ45 .η45
β
P rob4−5 =
α
τ45
.η45
β
α .η
α
α
α
α
τ12
12 + τ32 .η32 + τ35 .η35 + τ42 .η42 + τ45 .η45
1 ∗ 1, 522
1 ∗ 1, 522 + 1 ∗ 33, 332 + 1 ∗ 3, 72 + 1 ∗ 1, 962 + 1 ∗ 3, 032
1 ∗ 33, 332
1 ∗ 1, 522 + 1 ∗ 33, 332 + 1 ∗ 3, 72 + 1 ∗ 1, 962 + 1 ∗ 3, 032
1 ∗ 3, 72
1 ∗ 1, 522 + 1 ∗ 33, 332 + 1 ∗ 3, 72 + 1 ∗ 1, 962 + 1 ∗ 3, 032
1 ∗ 1, 962
1 ∗ 1, 522 + 1 ∗ 33, 332 + 1 ∗ 3, 72 + 1 ∗ 1, 962 + 1 ∗ 3, 032
1 ∗ 3, 032
1 ∗ 1, 522 + 1 ∗ 33, 332 + 11 ∗ 3, 72 + 1 ∗ 1, 962 + 1 ∗ 3, 032
= 0, 00203
= 0, 9745
= 0.012
= 0, 00337
= 0, 00805
Logo após do cálculo das probabilidades, a seguinte barras a ser visitada pela
formiga será determinada mediante um sorteio aleatório (roleta), Figura 4.8.
39
40
Capı́tulo 4. Metodologia Proposta
1-2 3-2 3-2 3-2 3-2 3-2
0,2%
...
3-2 3-2 3-5 4-2 4-5
1,2% 0,81%
0,33%
97,46%
Figura 4.8: Roleta aleatória para escolha entre os trechos 1-2, 3-2, 3-5, 4-2 e 4-5.
1
1
2
4
0
1
1
1
3
5
Figura 4.9: Sistema fictı́cio de 5 barras, deslocamento do agente desde a barra 3 até
a barra 2.
Supondo que a barra 5 seja a sorteada, então o trecho 3 − 5 será percorrido e a
barra 5 será ligada (um) como mostrado na Figura 4.9
Agora, têm-se que só a barra 2 esta barra pode ser escolhida por trechos diferentes
(trecho 1-2 ou trecho 3-2 ou trecho 4-2) e será novamente calculada as probabilidades
que tem cada trecho.
P rob1−2 =
P rob3−2 =
P rob4−2 =
β
α
τ12
.η12
1 ∗ 1, 522
=
= 0, 00206
β
β
β
2
α
α
α
1 ∗ 1, 52 + 1 ∗ 33, 332 + 1 ∗ 1, 962
τ12 .η12 + τ32 .η32 + τ42 .η42
β
α
τ32
.η32
1 ∗ 33, 332
=
= 0, 9944
β
β
β
2
α
α
α
1 ∗ 1, 52 + 1 ∗ 33, 332 + 1 ∗ 1, 962
τ12 .η12 + τ32 .η32 + τ42 .η42
β
α
τ42
.η42
1 ∗ 1, 962
=
= 0, 00343
β
β
α
α
α .η β
1 ∗ 1, 522 + 1 ∗ 33, 332 + 1 ∗ 1, 962
τ12 .η12 + τ32 .η32 + τ42
42
Logo após do cálculo das probabilidades, a seguinte barras a ser visitada pela
formiga será determinada mediante um sorteio aleatório (roleta), Figura 4.10.
Supondo que a barra 2 seja a sorteada mediante o trecho 1-2, então o trecho 1 − 2
será percorrido e a barra 2 será ligada (um) como mostrado na Figura 4.11 (a). Após
ser encontrada a nova configuração radial nenhuma formiga tem mais movimento
visto que já não existe mais barras desligadas. Portanto uma das configurações
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 4.4. Exemplo de Busca das configurações radiais
1-2 3-2 3-2 3-2 3-2 3-2
0,21%
...
41
3-2 3-2 4-2
0,34%
99,44%
Figura 4.10: Roleta aleatória para escolha entre os trechos 1-2, 3-2 e 4-2.
radiais é encontrada, Figura 4.11 (b), nessa configuração serão calculadas as perdas
do sistema e atualizada a quantidade de feromônio nos trechos que fazem parte da
configuração.
1
1
2
4
1
1
1
1
3
5
(a)
2
4
3
5
1
(b)
Figura 4.11: Sistema fictı́cio de 5 barras na inicialização do processo, (a) deslocamento do agente desde a barra 1 até a barra 2, (b) uma das configurações radiais
encontrada.
O processo do MMAS é mostrado na Figura 4.12. A variação no MMAS é usar
várias formigas para construir uma configuração de modo que é sempre radial. No algoritmo implementado, para os casos testados, é utilizado mais de uma configuração
por expedição para poder realizar a escolha de uma configuração (melhor solução)
por expedição.
41
42
Capı́tulo 4. Metodologia Proposta
INICIO
MMAS
Lê os dados do sistema
e os parâmetros do
MMAS e MSP
Calcula o limite máximo de
feromônio inicial (t max), utilizando
a perda ativa inicial do sistema
Feromônio inicial
t0 = tmax
Contador de expedição
exp=1
t ij = t max
Contador de comparação das soluções
k=1
Sim
Deposita a mesma quantidade de feromônio em
todos os ramos do sistemas
Persiste a
mesma solução em r?
k >= r
k=k+1
Não
Calcula feromônio máximo e mínimo
t max , t min
Contador do fluxo de carga para
escolha da melhor solução (m)
F=1
k=1
Começa o MMAS colocando uma
formiga em cada barra fonte
(subestação)
Não
Sim
Solução
Atual >= Anterior?
Calcula o fluxo de carga MSP
para o configuração radial
obtida
Calcula o valor das perdas
ativas da configuração
Calcula a função
objetivo
Guarda as soluções até um
valor determinado (m)
Se, tij > t max ; tij = t max
Sim
A formiga se desloca para a
barra ativável escolhido
F=F+1
Compara
Não
Aplica a regra de atualização do
feromônio com a melhor
solução escolhida
F>m
Sim
Sim
Escolhe a melhor solução do
conjunto de soluções guardada
Há ligações
ativáveis ?
Calcula a probabilidade só dos
ramos adjacentes de onde a
formiga esta no momento
exp=exp+1
Se , t ij < t min ; t ij = t min
Não
Não
Imprime a solução da função
objetivo, e as chaves desligadas
É a ultima
expedição ?
Fim
Figura 4.12: Fluxograma do Max-Min Ant System - MMAS para reconfiguração de
sistemas de distribuição de energia elétrica.
Huilman Sanca Sanca - Dissertação de Mestrado
Capı́tulo 5
Fluxo de Carga
Neste capı́tulo apresenta-se a análise do método utilizado para o desenvolvimento do estudo de fluxo de carga utilizado para o cálculo das perdas
de potência de sistemas de distribuição de energia elétrica. O cálculo de
fluxo de carga é necessário para o estudo de reconfiguração de redes e a
escolha do método utilizado é importante para garantir resultados de boa
qualidade e a sua eficiência computacional seja reduzida.
5.1
Introdução
O
S cálculos de fluxo de carga (ou fluxo de potência) são utilizados como
uma ferramenta essencial para a determinação dos parâmetros e condições
operacionais do sistema elétrico. o problema de fluxo de carga consiste na obtenção
de alguns parâmetros do estado de operação da rede (ângulo e magnitudes dos
fasores de tensão nodal) assim como na distribuição dos fluxos das potências.
Na literatura pode-se encontrar vários métodos de fluxo de carga, que, ao longo
dos anos têm sido propostas por diversos autores. O método mais conhecido pela
robustez que tem é o método de Newton Raphson e suas versões desacopladas,
porém este método precisa da construção e da inversão da matriz Jacobiana, o que
acrescenta um grande esforço computacional ao algoritmo.
Para resolver problemas de fluxo de carga em sistema de distribuição é possı́vel
usar o método de Newton Raphson. No entanto nos sistemas de distribuição de
energia elétrica, devido às particularidades inerentes a estes, como a alta relação
43
44
Capı́tulo 5. Fluxo de Carga
de resistência e reatância da linha R/X e a operação radial, estes métodos podem
apresentar problemas de convergência e se tornam ineficientes em alguns casos.
Uma alternativa seria a utilização dos métodos desacoplados que requerem muito
menos memória e apresentam menor esforço computacional. O problema com esses
métodos ocorre devido ao fato da relação R/X nos sistemas de distribuição ser
maior que nos sistemas de transmissão, o que leva a uma deterioração da dominância
diagonal das matrizes de rede (Guimarães, 2005). Na Tabela 5.1 é mostrada uma
comparação dos valores R/X para diferentes nı́veis de tensão.
Tabela 5.1: Relação R/X para diversos valores de tensão
Tensão (kV)
R/X
5.2
5.2.1
500
0, 056
440
0, 0770
345
0, 100
230
0, 200
138
0, 333
13, 8
2, 000
Fluxo de Carga para Sistemas de Distribuição
de Energia Elétrica
Modelo da Rede de Distribuição
Grande parte dos sistemas de distribuição de energia elétrica tem uma configuração fracamente malhada ou radial Figura 5.1. Para a formulação do modelo
da rede de distribuição de energia, é considerado que o sistema trifásico radial é
balanceado e pode ser representado por seu equivalente monofásico.
As linhas de distribuição são representadas por suas resistência e reatância série e
as capacitâncias em paralelo podem ser desprezadas nos nı́veis de tensão tı́picos do
sistema de distribuição, como ocorre na maioria dos casos práticos (Cespedes, 1990;
Cheng e Shirmohammadi, 1995).
5.2.2
Método de Soma de Potências - MSP
Em (Cespedes, 1990), sugeriu um método para resolver o problema de fluxo de
carga em sistemas de distribuição radial, o qual tinha os seguintes objetivos básicos.
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 5.2. Fluxo de Carga para Sistemas de Distribuição de Energia Elétrica
45
B5
C5
B1
C1
B2
4
1
B3
B4
2
3
SUBESTAÇÃO
C2
C3
C4
5
B6
B7
6
C6
C7
Figura 5.1: Exemplo de um sistema de distribuição de energia elétrica radial.
• o módulo da tensão de cada barra deve ser a variável de maior interesse,
prevalecendo sobre a sua fase; isto se justifica pelo fato de que, em sistemas
de distribuição, a diferença entre as fases das tensões de barra é pequena, de
alguns poucos graus;
• o método deve permitir a definição do módulo da tensão em qualquer barra do
alimentador, funcionando como uma restrição do problema de fluxo de carga,
e o cálculo das demais tensões de barra em função daquela;
• as cargas nas barras devem poder ser representadas como funções dos respectivos módulos das tensões nas barras;
• o método deve poder ser aplicado a problemas de fluxo de carga monofásico e
trifásico;
• por fim, o algoritmo deve ter seu tempo de processamento e convergência
compatı́veis com outros métodos usualmente utilizados para este problema de
fluxo de carga.
45
46
Capı́tulo 5. Fluxo de Carga
O método da soma de potência - MSP é um método de cálculo de fluxo de carga
iterativo nas variáveis perdas de potência ativa e reativa do tipo forward -backward
(Cespedes, 1990).
Se tivermos uma rede como o mostrado na Figura 5.2, se começa supondo que as
perdas em todos os trechos são nulas e em cada iteração as estimativas dessas perdas
vão melhorando. Com a tensão da barra da subestação sendo dada e as perdas
consideradas nulas, se calcula a tensão em todas as barras ligadas diretamente à
subestação (SE). Depois, se calculam as tensões em todas as barras ligadas àquelas
que estão ligadas diretamente à subestação (cujas tensões já foram calculadas) e
assim por diante. Findo esse primeiro estágio (forward ) se tem valores aproximados
de todas as tensões das barras. Aproximados porque foram calculados supondo
que as perdas eram nulas. Com os valores de tensão conhecidos, se calculam as
perdas em todos os trechos e então se corrigem os fluxos num processo (backward ).
O processo completo (forward-backward ) continua enquanto a variação nas perdas
totais for maior que uma tolerância previamente escolhida ou se eventualmente o
limite de iterações for excedido.
SE
1
2
3
i
i+1
i+2
Figura 5.2: Rede distribuição radial.
A solução do problema de fluxo de carga em um sistema radial usando o método
da soma de potência consiste em resolver, para cada trecho do alimentador, uma
equação de quarto grau em termos da tensão nodal. O processo de cálculo da
potência em um dado trecho consiste em somar os valores de potência (e daı́ vem
o nome do método) referentes às cargas e às perdas dos trechos que estão após o
trecho em estudo, incluindo a carga própria do mesmo (Guimarães, 2005).
Para a modelagem da rede de distribuição primária, o alimentador é dividido em
várias linhas ou ramos, os quais são limitados por nós ou barras, cada nó representando um ponto onde está instalado um transformador de distribuição. Se consideramos um trecho (i, i + 1) da Figura 5.2 obtemos a representação de um trecho
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 5.2. Fluxo de Carga para Sistemas de Distribuição de Energia Elétrica
47
do alimentador como mostrado na Figura 5.3.
Ii,i+1 ∠θi+1
Vi ∠δi
Vi+1 ∠δi+1
jXi,i+1
Ri,i+1
Pi+1 + jQi+1
i+1
i
PLi+1 + jQLi+1
PLi + jQLi
Figura 5.3: Trecho da rede distribuição radial para a aplicação do método de soma
de potências.
Sendo Vi ∠δi e Vi+1 ∠δi+1 , as tensões (módulo e ângulo) das barras (i, i + 1) respectivamente, Ii+1 ∠θi+1 é a corrente que atravessa o trecho (i, i + 1), Ri,i+1 e jXi,i+1
representam a resistência e a reatância do trecho (i, i+1) respectivamente, enquanto
que a carga instalada en cada barra (potência ativa e potência reativa) é representada por PLi + jQLi e PLi+1 + jQLi+1 . O fluxo de carga de potência do trecho
i + 1 é definido como aquele fluxo que circula ao final do mesmo Pi+1 + jQi+1 , logo
antes do seu nó terminal, não considerando as perdas correspondentes do trecho
∆Pi+1 , ∆Qi+1 ; é o fluxo de potência que chega ao final do trecho, já descontadas as
perdas do fluxo de carga disponı́vel no inı́cio do trecho.
A formulação matemática apresentada é realizado a partir da Figura 5.3, de onde
as seguintes equações são estabelecidas.
Ii,i+1 =
Vi ∠δi − Vi+1 ∠δi+1
Ri,i+1 + jXi,i+1
(5.1)
Sabe-se também que:
∗
∗
∗
Si+1 = Vi+1 .Ii,i+1
⇒ Si+1
= Vi+1
.Ii,i+1
(5.2)
Logo da equação(5.2) obtemos:
∗
Pi+1 − jQi+1 = Vi+1
.Ii,i+1 ⇒ Ii,i+1 =
Pi+1 − jQi+1
∗
Vi+1
(5.3)
47
48
Capı́tulo 5. Fluxo de Carga
Igualando as equações (5.1) e (5.3), correspondentes a Ii,i+1 , obtém-se:
Pi+1 − jQi+1
Vi ∠δi − Vi+1 ∠δi+1
Pi+1 − jQi+1
=
=
∗
Vi+1
Vi+1 ∠ − δi+1
Ri,i+1 + jXi,i+1
2
Vi .Vi+1 ∠(δi − δi+1 ) − Vi+1
= (Ri,i+1 + jXi,i+1 ).(Pi+1 − jQi+1 )
2
Vi .Vi+1 .[cos(δi − δi+1 ) + jsen(δi − δi+1 )] − Vi+1
= (Ri,i+1 + jXi,i+1 ).(Pi+1 − jQi+1 )
2
[Vi .Vi+1 .cos(δi − δi+1 ) − Vi+1
] + j[Vi .Vi+1 .sen(δi − δi+1 )]
= [Ri,i+1 .Pi+1 + Xi,i+1 .Qi+1 ] + j[Xi,i+1 .Pi+1 − Ri,i+1 .Qi+1 ]
(5.4)
Separando e igualando a parte real e a parte imaginária da equação (5.4), tem-se:
2
Vi .Vi+1 .cos(δi − δi+1 ) = Vi+1
+ Ri,i+1 .Pi+1 + Xi,i+1 .Qi+1
(5.5)
Vi .Vi+1 .sen(δi − δi+1 ) = Xi,i+1 .Pi+1 − Ri,i+1 .Qi+1
(5.6)
Elevando-se ao quadrado e somando-se as equações (5.5) e (5.6), obtemos o
seguinte:
2
2
Vi2 .Vi+1
= (Vi+1
+ Ri,i+1 .Pi+1 + Xi,i+1 .Qi+1 )2 + (Xi,i+1 .Pi+1 − Ri,i+1 .Qi+1 )2
2
4
2
Vi2 .Vi+1
= Vi+1
+ 2.Vi+1
.(Ri,i+1 .Pi+1 + Xi,i+1 .Qi+1 )
+(Ri,i+1 .Pi+1 + Xi,i+1 .Qi+1 )2 + (Xi,i+1 .Pi+1 − Ri,i+1 .Qi+1 )2
4
2
2
2
Vi+1
+ 2.[(Ri,i+1 .Pi+1 + Xi,i+1 .Qi+1 ) − 12 .Vi2 ]Vi+1
+ [(Ri,i+1
.Pi+1
+ 2(Ri,i+1 .Pi+1
2
2
2
2
2
.Xi,i+1 .Qi+1 ) + Xi,i+1 .Qi+1 )] + [Xi,i+1 .Pi+1 − 2(Xi,i+1 .Pi+1 .Ri,i+1 .Qi+1 ) + Ri,i+1
.Q2i+1 ] = 0
4
2
2
2
2
Vi+1
− 2.[ 12 .Vi2 − (Ri,i+1 .Pi+1 + Xi,i+1 .Qi+1 )]Vi+1
+ (Ri,i+1
+ Xi,i+1
).(Pi+1
+ Q2i+1 ) = 0
(5.7)
A equação (5.7) pode ser reescrita da seguinte forma:
Sendo
4
2
Vi+1
− 2.A.Vi+1
+B =0
(5.8)
1
A = .Vi2 − (Ri,i+1 .Pi+1 + Xi,i+1 .Qi+1 )
2
(5.9)
2
2
2
B = (Ri,i+1
+ Xi,i+1
).(Pi+1
+ Q2i+1 )
Huilman Sanca Sanca - Dissertação de Mestrado
(5.10)
Seção 5.2. Fluxo de Carga para Sistemas de Distribuição de Energia Elétrica
49
Em sistemas de distribuição, as fases das tensões não são de grande importância,
pois a diferença de fase entre a barra da subestação e a última barra do alimentador
geralmente é de apenas alguns graus (Cespedes, 1990; Cheng e Shirmohammadi,
1995; Guimarães, 2005), então a equação(5.8) tem uma solução direta e que não
depende da fase das tensões das barras, o que simplifica a formulação do problema.
É interessante observar que a equação (5.8) é biquadrada, possui quatro raı́zes.
2
Entretanto, das duas soluções para Vi+1
, apenas aquela que considera o sinal positivo
da raiz quadrada da solução fornece um valor de tensão possı́vel de se encontrar na
prática; o mesmo se aplica à raiz quadrada da solução para Vi+1 (Cespedes, 1990).
Resolvendo a equação(5.8) obtemos:
Vi+1 =
q
A+
√
A2 − B
(5.11)
Sendo que A e B estão indicados nas equações (5.9) e (5.12) respectivamente.
Tendo calculado as tensões em todas as barras do alimentador disponı́veis, é
possı́vel então calcular as perdas ativa e reativa em cada trecho da seguinte forma:
∆Pi+1 =
2
Ri,i+1 Ii,i+1
∆Qi+1 =
2
Xi,i+1 Ii,i+1
⇒ ∆Pi+1 = Ri,i+1
⇒ ∆Qi+1 = Xi,i+1
Si+1
Vi+1
Si+1
Vi+1
2
2
⇒ ∆Pi+1 = Ri,i+1
⇒ ∆Qi+1 = Xi,i+1
2
Pi+1
+ Q2i+1
Vi+1
2
Pi+1
+ Q2i+1
Vi+1
Assim sendo, as perdas ativa e reativa para o trecho (i, i + 1) do alimentador é
fornecido pelas equações (5.12) e (5.13), respectivamente.
2
Pi+1
+ Q2i+1
Vi+1
PP erdas (i, i + 1) = ∆Pi+1 = Ri,i+1
QP erdas (i, i + 1) = ∆Qi+1 = Xi,i+1
2
Pi+1
+ Q2i+1
Vi+1
(5.12)
(5.13)
A perda de potência ativa e reativa total do sistema PT,P erdas , QT,P erdas , é a soma
das perdas de potência de todos os trechos do sistema como é mostrado nas equações
(5.14) e (5.15), respectivamente.
49
50
Capı́tulo 5. Fluxo de Carga
PT,P erdas =
NX
B −1
Pperdas (i, i + 1)
(5.14)
NX
B −1
Qperdas (i, i + 1)
(5.15)
i=1
QT,P erdas =
i=1
Onde PT,perdas e QT,perdas são as perdas de potência ativa e reativa totais do
sistema, NB é o número de barras do sistema.
Inicio
MSP
Lê os dados da rede
Assumir perfil de tensão inicial
V0
Calcula as cargas que
dependem da tensão
Inicio do processo
Backward
Calcula a potência equivalente
em cada barra
Inicio do processo
Forward
Calcula o novo perfil
de tensões das barras
Calcula as perdas do sistema
Pperdas = = Pperdas2 – Pperdas1
Convergiu?
= tol ?
Sim
Imprime os
resultado
Fim
MSP
Não
Pperdas1 = Pperdas2
Calcula V
Calcua V (V=V0- V)
Figura 5.4: Algoritmo do fluxo de carga método de soma de potências - MSP, do
tipo Backward - Forward.
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 5.3. Teste Fluxo de Carga MSP
5.3
51
Teste Fluxo de Carga MSP
5.3.1
Sistema de 33 barras
O sistema teste de 33 barras foi tomado de (Baran e Wu., 1989), o método implementado para o fluxo de carga, MSP, convergiu em três (3) iterações, os valores
das perdas de potência ativa e reativa foram de 202,98 kW e 135,1 kVAR, respectivamente. Os valores das tensões por barra são apresentados na Tabela 5.2.
Tabela 5.2: Tensões da configuração inicial para o sistema de 33 barras.
Barra
1
2
3
4
5
6
7
8
9
10
11
Tensão (pu)
1,000000
0,997033
0,982939
0,975458
0,968062
0,949661
0,946175
0,941331
0,935062
0,929247
0,928387
Barra
12
13
14
15
16
17
18
19
20
21
22
Tensão (pu)
0,926888
0,920775
0,918508
0,917096
0,915728
0,913700
0,913093
0,996504
0,992927
0,992222
0,991585
Barra
23
24
25
26
27
28
29
30
31
32
33
Tensão (pu)
0,979354
0,972683
0,969358
0,947732
0,945168
0,933728
0,925510
0,921953
0,917792
0,916876
0,916593
Na Figura 5.5, é apresentado o perfil das tensões nas barras determinado pelo
Tensão (p.u.)
fluxo de carga MSP para a configuração inicial do sistema de 33 barras.
Barras
Figura 5.5: Perfil da tesão para a configuração inicial do sistema de 33 barras.
51
52
Capı́tulo 5. Fluxo de Carga
5.3.2
Sistema de 69 barras
O sistema teste de 69 barras foi tomado de (Chiang e Jeam-Jumeau, 1990), o
método implementado para o fluxo de carga, MSP, convergiu em duas (2) iterações,
os valores das perdas de potência ativa e reativa foram de 20,91 kW e 9,40 kVAR,
respectivamente. Os valores das tensões por barra são apresentados na Tabela 5.3.
Tabela 5.3: Tensões da configuração inicial para o sistema de 69 barras.
Barra
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Tensão (pu)
1,000000
0,999990
0,999979
0,999951
0,999696
0,996958
0,994109
0,993431
0,993085
0,991493
0,991143
0,990148
0,989246
0,988353
0,987470
0,987306
0,987038
0,987035
0,986884
0,986788
0,986632
0,986629
0,986606
Barra
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
Tensão (pu)
0,986556
0,986501
0,986478
0,986472
0,999977
0,999954
0,999914
0,999907
0,999872
0,999788
0,999677
0,999656
0,999975
0,999926
0,999886
0,999875
0,999874
0,999733
0,999674
0,999666
0,999665
0,999645
0,999645
Barra
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
Tensão (pu)
0,999936
0,999576
0,998482
0,998301
0,993419
0,993416
0,992251
0,991281
0,989944
0,988640
0,981967
0,978680
0,977408
0,975840
0,973531
0,973441
0,973320
0,972729
0,972550
0,991125
0,991125
0,990040
0,990040
Na Figura 5.6, é apresentado o perfil das tensões nas barras determinado pelo
fluxo de carga MSP para a configuração inicial do sistema de 69 barras.
Huilman Sanca Sanca - Dissertação de Mestrado
53
Tensão (p.u.)
Seção 5.3. Teste Fluxo de Carga MSP
Barras
Figura 5.6: Perfil da tesão para a configuração inicial do sistema de 69 barras.
5.3.3
Sistema de 136 barras
O sistema teste de 136 barras foi tomado de (Mantovani et al., 2000), o método
implementado para o fluxo de carga, MSP, convergiu em duas (3) iterações, os valores
das perdas de potência ativa e reativa foram de 321,5 kW. Os valores das tensões
por barra são apresentados na Tabela 5.4 e Tabela 5.5.
Tabela 5.4: Tensões da configuração inicial para o sistema de 136 barras, (a).
Barra
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
Tensão (pu)
1,000000
0,990973
0,990922
0,985002
0,982420
0,978528
0,974986
0,974704
0,974257
0,973833
0,973012
0,972708
0,971608
0,972111
0,971113
Barra
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
Tensão (pu)
0,971934
0,971552
0,991300
0,991251
0,985431
0,982603
0,981499
0,978427
0,977954
0,977949
0,977130
0,976788
0,975339
0,975119
0,974886
Barra
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
Tensão (pu)
0,974732
0,974672
0,974362
0,973239
0,972933
0,974369
0,973307
0,972871
0,974335
0,990851
0,987612
0,987498
0,987560
0,985668
0,985335
Barra
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
Tensão (pu)
0,984053
0,980974
0,979826
0,978300
0,978063
0,977826
0,977865
0,977611
0,977388
0,977359
0,977354
0,977049
0,976232
0,974958
0,973921
53
54
Capı́tulo 5. Fluxo de Carga
Tabela 5.5: Tensões da configuração inicial para o sistema de 136 barras, (b).
Barra
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
Tensão (pu)
0,973719
0,973719
0,979492
0,999879
0,995540
0,990557
0,986554
0,982866
0,981135
0,980835
0,980701
0,980572
0,980539
0,980368
0,977086
0,999800
0,986893
0,983178
0,980065
Barra
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
Tensão (pu)
0,979412
0,974647
0,972398
0,972070
0,971986
0,971055
0,999665
0,987302
0,986316
0,980100
0,979354
0,978784
0,976330
0,975779
0,975033
0,974024
0,973400
0,973111
0,974949
Barra
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
Tensão (pu)
0,974839
0,999677
0,993866
0,989877
0,989751
0,974928
0,952468
0,938824
0,936767
0,935186
0,933445
0,933445
0,935064
0,934717
0,934447
0,934447
0,931257
0,929386
0,927482
Barra
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
Tensão (pu)
0,927482
0,951894
0,951745
0,951663
0,999739
0,984754
0,983769
0,983365
0,983358
0,982840
0,981666
0,981565
0,979414
0,978826
0,977614
0,975947
0,974176
0,973381
0,973381
Na Figura 5.7, é apresentado o perfil das tensões nas barras determinado pelo
Tensão (p.u.)
fluxo de carga MSP para a configuração inicial do sistema de 136 barras.
Barras
Figura 5.7: Perfil da tesão para a configuração inicial do sistema de 136 barras.
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 5.4. Conclusão do Capı́tulo
5.4
55
Conclusão do Capı́tulo
Neste capı́tulo apresentou-se uma abordagem para a resolução do problema de
fluxo de carga aplicando o método de soma de potências para sistemas de distribuição
de energia elétrica radiais. A vantagem deste método é que ela incorpora a topologia
radial do sistema para o processo de cálculo de fluxo de carga, outra das vantagens
do método de soma de potências é a capacidade de encontrar a solução do problema
(convergência) em um número reduzido de iterações. Assim também foi apresentado
os resultados dos fluxos de carga das topologias iniciais dos sistemas testados. Estes
resultados apresentam os nı́veis de tensão nas barras e as perdas de potência totais,
que serão reduzidas ao aplicar a reconfiguração para achar uma nova topologia que
tenha menor valor de perdas ativas das achadas inicialmente neste capı́tulo.
55
56
Huilman Sanca Sanca - Dissertação de Mestrado
Capı́tulo 5. Fluxo de Carga
Capı́tulo 6
Testes e Resultados
Neste capı́tulo apresenta-se a avaliação e testes do algoritmo Max-Min
Ant System - MMAS aplicado para reconfiguração de redes. Os testes
realizados foram feitos em três casos (sistemas de distribuição), e os resultados são comparados com resultados obtidos em alguns trabalhos que,
utilizando métodos diferentes, fizeram a aplicação nestes três sistemas.
6.1
Estudo de Casos
Tendo visto nos capı́tulos anteriores um estudo para a aplicação do algoritmo MaxMin Ant System - MMAS ao problema de reconfiguração de sistemas de distribuição
de energia elétrica, neste capı́tulo são apresentados os resultados obtidos da aplicação
do método implementado, MMAS, para a minimização de perdas ativas. Para efeito
de verificação do desempenho, o algoritmo MMAS, é aplicado a três sistemas de
distribuição, os quais são: 33 barras (Baran e Wu., 1989), 60 barras (Chiang e JeamJumeau, 1990) e 136 barras (Mantovani et al., 2000). Os resultados obtidos após a
reconfiguração obtida pelo MMAS foram comparados com soluções encontradas na
literatura.
O algoritmo para fluxo de carga, método de soma de potências - MSP, e o algoritmo Max-Min Ant System - MMAS para reconfiguração de sistemas de distribuição
foram implementados em Matlabr em um computador Intel Core i5-2410M 2.3 GHz
e 6 GB. Os parâmetros utilizados no algoritmo são apresentados na Tabela 6.1. No
algoritmo implementado, em cada expedição se faz uma escolha da melhor solução
57
58
Capı́tulo 6. Testes e Resultados
gerada nesse momento e que será depois utilizada para a atualização do feromônio.
As soluções encontradas durante a execução do algoritmo que não respeitaram as
restrições do problema foram descartadas.
Tabela 6.1: Parâmetros utilizados para o algoritmo nos sistemas de distribuição
testados.
33 barras
69 barras
Parâmetros
Dado Valor Dado Valor
Peso (carga do feromônio)
α
0,1
α
0,1
Peso da visibilidade
β
4,6
β
1
ρ
0,1
ρ
0,1
Taxa de evaporação
Tolerância do MSP
ε
10−3
ε
10−3
Expedições
200
200
Perda ativa inicial (kW)
F∗
202,68
F∗
20,9
Número de barras da rede
n
33
n
69
Melhor probabilidade
Pmelhor
0,05 Pmelhor
0,05
Feromônio inicial
τ0
0,049
τ0
0,48
Média de barras candidatas
k
1
k
1
6.2
136 barras
Dado Valor
α
0,3
β
4
ρ
0,01
ε
10−3
100
F∗
321,5
n
136
Pmelhor
0,05
τ0
0,0311
k
1
Sistema Teste de 33 barras
O sistemas de distribuição teste de 33 barras foi tomado de (Baran e Wu., 1989),
tem uma tensão nominal de 12,66 kV. Este sistema possui 33 barras (barra 1 é a
subestação), 5 laços de interconexão e 37 chaves seccionadoras, sendo originalmente
32 chaves fechadas (chaves de 1 a 32) e 5 chaves abertas (chaves de 33 a 37), conforme
é apresentado na Figura 6.1. Para esta configuração inicial a topologia apresenta
202,98 kW de perdas ativas. A condição necessária, porém não suficiente para que
a rede seja radial, é que 5 das 37 ligações (chaves) sejam desativadas (abertas), pois
as barras de carga são 33. Os dados das potências instaladas nas barras e os dados
dos valores das resistências e reatâncias das linhas (trechos de rede) podem ser encontrados no apêndice B.
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 6.2. Sistema Teste de 33 barras
19
20
s19
21
s20
Subestação
2
s1
Barra (nós)
Ligações ativadas
Ligações interrompidas
sN Chaves seccionadores
22
s35
s21
s18
1
59
s33
3
4
s3
s2
5
s4
6
s5
8
7
s6
9
s7
s8
10
s9
11
s10
12
s11
13
s12
14
s13
s14
15
16
s15
s16
17
s34
s25
s22
s17
26
27
s26
23
24
s23
28
s27
29
s28
s29
30
31
s30
s31
32
18
33
s32
s36
25
s24
s37
Figura 6.1: Configuração inicial do sistema de distribuição de 33 barras e 37 ligações.
Perdas de potência (kW)
O processo de convergência do algoritmo é mostrado na Figura 6.2.
Solução encontrada
Expedições
Figura 6.2: Evolução do processo de convergência do algoritmo MMAS, perdas totais
versus expedições, sistema de 33 barras.
A Tabela 6.2 apresenta os resultados da melhor configuração obtida após a corrida
do algoritmo desenvolvido. Os resultados obtidos pelo algoritmo Max-Min Ant System - MMAS mostram a vantagem que tem ao encontrar uma melhor configuração
59
60
Capı́tulo 6. Testes e Resultados
(solução) ao problema de reconfiguração, sendo que as perdas ativas totais para a
configuração inicial do sistema é de 202,68 kW, enquanto, para a configuração encontrada pelo algoritmo implementado as perdas de potência ativa foram de 134,66 kW,
isto equivale a uma redução de 33,66% da perda de potência ativa total inicial. Estes
resultados foram comparados com os resultados encontrados na literatura (Baran
e Wu., 1989; Mantovani et al., 2000; Lorenzeti, 2004; Guimarães, 2005; Gomes et
al., 2006; Srinivasa e Narasimhan, 2009).
Tabela 6.2: Comparação de resultados obtidos para a reconfiguração do sistema de
33 barras.
Configuração
Initial
MMAS, implementado
(Srinivasa et al., 2009)
(Gomes et al., 2006)
(Guimarães, 2005)
(Lorenzeti, 2004)
(Mantovani et al., 2000)
(Baran e Wu., 1989)
Perdas
(kW)
202,68
134,66
135,78
136,57
136.57
140,71
139,55
160.99
Redução
(%)
--33,66
33,11
32,72
32,72
30,67
31,25
20,52
Chaves desligadas
s33, s34,
s7, s9,
s8, s14,
s7, s9,
s7, s9,
s7, s10,
s7, s9,
s7, s10,
s35,
s16,
s28,
s14,
s14,
s14,
s14,
s14,
s36,
s28,
s32,
s32,
s32,
s28,
s32,
s27,
s37
s34
s33
s37
s37
s32
s37
s30
Na Figura 6.3, apresenta-se uma comparação do perfil das tensões em cada barra
da configuração inicial e da configuração encontrada pelo algoritmo MMAS implementado. Neste perfil de tensões é mostrado com maior clareza a melhora e a
vantagem obtida pelo algoritmo.
Esta redução da perda de potência ativa e melhora no perfil das tensões do sistema é resultado da reconfiguração de redes que foi alcançado desativando as chaves
seccionadoras s7, s9, s16, s28, s34, que equivalem aos trechos das barras: 7-8, 9-10,
16-17, 28-29, 9-15 respectivamente como mostrado na Figura 6.4.
Huilman Sanca Sanca - Dissertação de Mestrado
61
Tensão (p.u.)
Seção 6.3. Sistema Teste de 69 barras
Barras do sistema
Figura 6.3: Comparação do perfil da tensão em cada barra da configuração inicial
e da configuração final encontrada pelo algoritmo MAX-MIN Ant System - MMAS
implementado, sistema de 33 barras.
19
20
s19
21
s20
s35
s21
Subestação
s18
1
2
s1
Barra (nós)
Ligações ativadas
Ligações interrompidas
sN Chaves seccionadores
22
s33
3
4
s3
s2
5
s4
6
s5
8
7
s6
9
s8
s7
10
s9
11
s10
12
s11
13
s12
14
s13
s14
15
16
s15
s16
17
s34
s25
s22
s17
26
27
s26
23
24
s23
28
s27
29
s28
s29
30
31
s30
s31
32
s32
18
33
s36
25
s24
s37
Figura 6.4: Rede de distribuição reconfigurada obtida pelo algoritmo MAX-MIN
Ant System - MMAS implementado, sistema de 33 barras.
6.3
Sistema Teste de 69 barras
O sistemas de distribuição teste de 69 barras foi tomado de (Chiang e JeamJumeau, 1990), tem uma tensão nominal de 12,66 kV. Este sistema possui 69 barras
(barra 1 é a subestação), 5 laços de interconexão e 73 chaves seccionadoras, sendo
originalmente 68 chaves fechadas (chaves de 1 a 68) e 5 chaves abertas (chaves de
61
62
Capı́tulo 6. Testes e Resultados
69 a 73), conforme é apresentado na Figura 6.5. Para esta configuração inicial a
topologia apresenta 20,9 kW de perdas ativas. A condição necessária, porém não
suficiente para que a rede seja radial, é que 5 das 73 ligações (chaves) sejam desativadas (abertas), pois as barras de carga são 69. Os dados das potências instaladas
nas barras e os dados dos valores das resistências e reatâncias das linhas (trechos de
rede) podem ser encontrados no apêndice B.
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
51
52
44
45
46
Subestação
s69
1
2
3
4
5
6
7
8
9
10
11
12
66 67
sN
Barra (nó)
Ligações ativadas
Ligações interrompidas
Chaves seccionadores
19
20
s71
13
14
15
16
17
18
21
22
23
24
25
26
27
s70
68 69
s73
47
48
49
50
53
54
55
56
57
58
59
60
61
62
63
64
65
s72
Figura 6.5: Configuração inicial do sistema de distribuição de 69 barras e 73 ligações.
Perdas de potência (kW)
O processo de convergência do algoritmo é mostrado na Figura 6.6.
Solução encontrada
Expedições
Figura 6.6: Evolução do processo de convergência do algoritmo MMAS, perdas totais
versus expedições, sistema de 69 barras.
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 6.3. Sistema Teste de 69 barras
63
A Tabela 6.3 apresenta os resultados da melhor configuração obtida após a corrida
do algoritmo desenvolvido. Os resultados obtidos pelo algoritmo Max-Min Ant System - MMAS mostram a vantagem que tem ao encontrar uma melhor configuração
(solução) ao problema de reconfiguração, sendo que as perdas ativas totais para a
configuração inicial do sistema é de 20,91 kW, enquanto, para a configuração encontrada pelo algoritmo implementado as perdas de potência ativa foram de 9,39 kW,
isto equivale a uma redução de 55,10% da perda de potência ativa total inicial. Estes
resultados foram comparados com os resultados encontrados na literatura (Chiang e
Jeam-Jumeau, 1990; Lorenzeti, 2004; Guimarães, 2005; Abdelaziz. et al., 2010; Abdelaziz et al., 2012).
Tabela 6.3: Comparação de resultados obtidos para a reconfiguração do sistema de
69 barras.
Configuração
Perdas Redução
(kW)
(%)
Initial
20,9
--MMAS, implementado
9,39
55,10
(Abdelaziz et al., 2012)
9,43
54,88
(Abdelaziz. et al., 2010)
9,40
55,00
(Guimarães, 2005)
9,41
54,97
(Lorenzeti, 2004)
9,42
54,95
(Chiang e Jeam-Jumeau, 1990)
9,41
54,97
Chaves desligadas
s69,
s12,
s14,
s12,
s15,
s14,
s14,
s70,
s57,
s58,
s55,
s59,
s58,
s55,
s71,
s63,
s61,
s61,
s62,
s62,
s61,
s72,
s69,
s69,
s69,
s70,
s70,
s69,
s73
s70
s70
s70
s71
s71
s70
Na Figura 6.7, apresenta-se uma comparação do perfil das tensões em cada barra
da configuração inicial e da configuração encontrada pelo algoritmo MMAS implementado. Neste perfil de tensões é mostrado com maior clareza a melhora e a
vantagem obtida pelo algoritmo.
Esta redução da perda de potência ativa e melhora no perfil das tensões do sistema é resultado da reconfiguração de redes que foi alcançado desativando as chaves
seccionadoras s12, s57, s63, s69, s70, que equivalem aos trechos das barras: 12-13,
57-58, 63-64, 11-43, 13-21 respectivamente como mostrado na Figura 6.8.
63
Capı́tulo 6. Testes e Resultados
Tensão (p.u.)
64
Barras do sistema
Figura 6.7: Comparação do perfil da tensão em cada barra da configuração inicial
e da configuração final encontrada pelo algoritmo MAX-MIN Ant System - MMAS
implementado, sistema de 69 barras.
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
51
52
44
45
46
Subestação
s69
1
2
3
4
5
6
7
8
9
10
11
sN
Barra (nó)
Ligações ativadas
Ligações interrompidas
Chaves seccionadores
18
19
20
21
22
61
62
63 64
s63
65
s71
12 13
s12
14
66 67
68 69
54
56
15
16
17
23
24
25
26
27
s70
s73
47
48
49
50
53
55
57 58
s57
59
60
s72
Figura 6.8: Rede de distribuição reconfigurada obtida pelo algoritmo MAX-MIN
Ant System - MMAS implementado, sistema de 69 barras.
6.4
Sistema Teste de 136 barras
O sistemas de distribuição teste de 136 barras é um sistema real da cidade de
Três Lagoas - MS, cujos dados foram tomados de (Mantovani et al., 2000), têm uma
tensão nominal de 13,8 kV. Este sistema possui 136 barras (barra 1 é a subestação),
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 6.4. Sistema Teste de 136 barras
65
21 laços de interconexão e 156 chaves seccionadoras, sendo originalmente 135 chaves
fechadas (chaves de 1 a 135) e 21 chaves abertas (chaves de 135 a 156), conforme
é apresentado na Figura 6.9. Para esta configuração inicial a topologia apresenta
321,5 kW de perdas ativas.
s136
8
74
12
71
69 68 67 66
65
s144
3
4
5
6
7
9
Barra (nó)
Ligações ativadas
Ligações interrompidas
Chaves seccionadores
75
73
11 14 16
72
70
sN
83
s138
22
24
s137
10 13
15 17
s146 85 84
82
81 80
s145
s139
20
21 23
25 26 27
28 29 30 31
136 135 134 133 132
64
39 s156
s140
35
2
34 33 32
36 37
38
79 78 77 76
s155 s154
s151
s142
52 53
18 19
54 55
56
99 98
129 127
40
57
41 42
58
59 60 61
1
62
131 130 128 126 124 123 122
s148
1
43
44
46 47 48 49
s141
50 51
97
45
s152
s153
96
95
94 93
92 91 90
89 87 86
1
s150 s147 s149
88
s143
63
121 120 119 105 104 102 101 100
114 113 112 111 108 107 106
103
118 117 110 109 115 116
Figura 6.9: Configuração inicial do sistema de distribuição de 136 barras e 156
ligações.
A condição necessária, porém não suficiente para que a rede seja radial, é que
21 das 156 ligações (chaves) sejam desativadas (abertas), pois as barras de carga
são 136. Os dados das potências instaladas nas barras e os dados dos valores das
resistências e reatâncias das linhas (trechos de rede) podem ser encontrados no
apêndice B.
65
66
Capı́tulo 6. Testes e Resultados
Perdas de potência (kW)
O processo de convergência do algoritmo é mostrado na Figura 6.10.
Solução encontrada
Expedições
Figura 6.10: Evolução do processo de convergência do algoritmo MMAS, perdas
totais versus expedições, sistema de 136 barras.
A Tabela 6.4 apresenta os resultados da melhor configuração obtida após a corrida
do algoritmo desenvolvido. Os resultados obtidos pelo algoritmo Max-Min Ant System - MMAS mostram a vantagem que têm ao encontrar uma melhor configuração
(solução) ao problema de reconfiguração, sendo que as perdas ativas totais para a
configuração inicial do sistema é de 321,50 kW, enquanto, para a configuração encontrada pelo algoritmo implementado as perdas de potência ativa foram de 286,55
kW, isto equivale a uma redução de 10,87% da perda de potência ativa total inicial. Estes resultados foram comparados com os resultados encontrados na literatura
(Mantovani et al., 2000; Guimarães, 2005; Lorenzeti, 2004). Verifica-se que o algoritmo implementado encontrou uma solução próxima em comparação com os outros
métodos, isto devido a que o processo de busca da solução tornou-se mais complicado para este sistema que tem maior número de chaves a serem desativas.
Na
Figura 6.11, apresenta-se uma comparação do perfil das tensões em cada barra da
configuração inicial e da configuração encontrada pelo algoritmo MMAS implementado. Neste perfil de tensões é mostrado com maior clareza a melhora e a vantagem
obtida pelo algoritmo.
Huilman Sanca Sanca - Dissertação de Mestrado
Seção 6.4. Sistema Teste de 136 barras
67
Tabela 6.4: Comparação de resultados obtidos para a reconfiguração do sistema de
136 barras.
Configuração
Perdas
(kW)
321,5
Redução
(%)
---
MMAS
286,55
10,87
(Guimarães, 2005)
280,23
12,84
(Lorenzeti, 2004)
284,46
11,52
(Mantovani et al., 2000)
285,50
11,19
s136, s137, s138, s139, s140, s141,
s143, s144, s145, s146, s147, s148,
s150, s151, s152, s153, s154, s155,
s38, s51, s53, s83, s84, s106,
s128, s136, s137, s141, s144, s145,
s148, s149, s150, s151, s152, s154,
s7, s38, s51, s53, s90, s96,
s118, s126, s137, s138, s141, s144,
s146, s147, s148, s150, s151, s155,
s38, s51, s53, s106, s119, s136,
s138, s141, s144, s145, s146, s147,
s149, s150, s151, s152, s154, s155,
s51, s136, s137, s138, s139, s141,
s143, s144, s145, s146, s147, s148,
s150, s151, s152, s106, s154, s155,
s142
s149
s156
s118
s147
s156
s106
s145
s156
s137
s148
s156
s142
s149
s156
Tensão (p.u.)
Initial
Chaves desligadas
Barras do sistema
Figura 6.11: Comparação do perfil da tensão em cada barra da configuração inicial
e da configuração final encontrada pelo algoritmo MAX-MIN Ant System - MMAS
implementado, sistema de 136 barras.
67
68
Capı́tulo 6. Testes e Resultados
Esta redução da perda de potência ativa e melhora no perfil das tensões do sistema é resultado da reconfiguração de redes que foi alcançado desativando as chaves
seccionadoras s38, s51, s53, s83, s84, s106, s118, s128, s136, s137, s141, s144, s145,
s147, s148, s149, s150,s151, s152, s154, 156s, que equivalem aos trechos das barras
mostradas na Figura 6.12.
s136
8
74
71
69 68 67 66
73
72
70
65
sN
s144
3
4
5
6
7
9
Barra (nó)
Ligações ativadas
Ligações interrompidas
Chaves seccionadores
75
12
11 14 16
83
s138
22
24
s137
10 13
s84 s83
s146 85 84 82
15 17
81 80
s145
s139
20
21 23
136 135 134 133 132
28 29 30 31
s38
39 s156
25 26 27
s140
35
2
34 33 32
36 37
52 53
79 78 77 76
s155 s154
s151
s142
s53
18 19
38
64
54 55
99 98
56
s128 129 127
s51
40
57
41 42
58
59 60 61
1
62
131 130 128 126 124 123 122
s148
1
43
44
46 47 48 49
s141
50 51
97
45
s152
s153
96
95
94 93
92 91 90
89 87 86
1
s150 s147 s149
s143
88
s118
63
s106
121 120 119 105 104 102 101 100
114 113 112 111 108 107 106
103
118 117 110 109 115 116
Figura 6.12: Rede de distribuição reconfigurada obtida pelo algoritmo MAX-MIN
Ant System - MMAS implementado, sistema de 136 barras.
6.5
Conclusão do Capı́tulo
Neste capı́tulo foram apresentados os teste e resultados obtidos pelo método implementado MMAS, cujas simulações foram realizadas em sistemas de distribuição
de energia elétrica conhecidas na literatura de reconfiguração de redes. Finalmente
no capı́tulo seguinte é apresentado as conclusões deste trabalho e algumas perspectivas para trabalhos futuros.
Huilman Sanca Sanca - Dissertação de Mestrado
Capı́tulo 7
Conclusões e Trabalhos Futuros
U
MA variante do algoritmo colônia de formigas o MAX-MIN Ant System MMAS foi apresentado. Esta meta-heurı́stica é utilizada para a resolução do
problema de reconfiguração de sistemas de distribuição de energia elétrica. Esta
metodologia apresenta como principal caracterı́stica uma intensa exploração em
torno das melhores soluções.
Inicialmente apresentaram-se alguns dos principais trabalhos e metodologias para
a reconfiguração de sistemas de distribuição encontrados na literatura. Apresentouse também um estudo do algoritmo colônia de formigas e suas variantes, sistema de
formigas Ant System - AS, colônia de formigas com elitismo Elitist Ant System EAS, colônia de formigas Ant Colony System - ACS e o algoritmo implementado
neste trabalho o MAX-MIN Ant System - MMAS.
Para verificar o desempenho do algoritmo e realizar uma validação foram utilizados teste em três (3) sistemas de distribuição, contendo 33, 69 e 136 barras. Em
particular o sistema de 136 barras é um sistema real da cidade de Três Lagoas do
estado de Mato Grosso do Sul.
Os resultados obtidos pelo algoritmo implementado MAX-MIN Ant System MMAS são compatı́veis com a literatura, sendo que as soluções encontradas para os
sistemas testados foram muito próximos e até em alguns dos casos melhores que os
resultados encontrados na literatura. Então é possı́vel dizer que o desempenho do
algoritmo implementado é satisfatório nos testes realizados para os sistemas elétricos
propostos. De modo que se conclui que a metodologia proposta é confiável, eficiente
e robusta para resolver problemas de reconfiguração de sistemas de distribuição de
69
70
Capı́tulo 7. Conclusões e Trabalhos Futuros
energia elétrica.
Os bons resultados obtidos credencia o método como muito promisor para as
concessionárias de energia elétrica uma vez que ela mostra as possibilidades de encontrar configurações que apresentam menor valor das perdas de potência ativa e
uma melhora no perfil de tensão do sistema.
7.1
Sugestões de Futuros Trabalhos
(i) Com o fim de melhorar a eficiência do algoritmo pode-se estudar uma técnica de
processamento paralelo, pode ser considerado a implementação de um FPGA,
que é um processamento de informações, e que pode ajudar a encontrar as
soluções em tempos reduzidos de sistemas ainda maiores.
(ii) Sugere-se implementar uma função objetivo adicionando uma restrição de limites de tensão nas barras, isto para evitar configurações com quedas de tensão
elevados nas barras e garantir nı́veis de tensão adequados.
(iii) Sugere-se aprofundar os estudos na realização de um algoritmo hı́brido usando
busca local, isto pode ser feito mediante a implementação do um algoritmo
de busca tabu, Tabu Search, que ajude a realizar uma busca exaustiva das
soluções.
(iv) Com o fim de poder adaptar estes sistemas a novas fontes de geração de energia
renováveis, sugere-se realizar um estudo da aplicação da geração distribuı́da
(GD) ou geração dispersa nos sistemas de distribuição. Assim também realizar
o controle destas aplicando redes inteligentes (Smart Grid ).
(v) Tratando-se a reconfiguração ótima de sistemas de distribuição de energia
elétrica um problema de redução de perdas de potência ativa, sugere-se realizar
um estudo econômico para avaliar quanto economiza uma rede de distribuição
reconfigurada.
Huilman Sanca Sanca - Dissertação de Mestrado
Referências Bibliográficas
Abdelaziz, A. Y., R. A. Osama e S. M. El-khodary (2012). Reconfiguration of distribution system for loss reduction using the hyper-cube ant colony optimization
algorithm. IEEE Generation, Transmition and Distribution - IET 6(2), 176–
187.
Abdelaziz., A.Y., F.M. Mohamed, S.F. Mekhamer e M.A.L. Badr (2010). Distribution system reconfiguration using a modified tabu search algorithm. Electric
Power System Research 80(1), 943–953.
Baran, M. E. e Felix F. Wu. (1989). Network reconfiguration in distribution system
for loss reduction and load balancing. IEEE Transaction on Power Delivery
4(2), 1401–1407.
Bueno, E. A. (2005). Redução de perdas técnicas através de reconfigurações de redes
de distribuição de energia elétrica sob demandas variáveis. Tese (Doutorado em
engenharia elétrica)- Faculdade de engenharia elétrica e computação, Universidade de Campinas, Campinas pp. 1–148.
Cavellucci, C. (1998). Buscas informadas baseadas em grafos para minimização de
perdas em sistemas de distribuição de energia elétrica. Tese (Doutorado em
engenharia elétrica)- Faculdade de engenharia elétrica e computação da Universidade de Campinas, Campinas-SP pp. 1–139f.
Cespedes, R. G. (1990). New method for the analysis of distribution netwok. IEEE
Transactions on Power Delivery 5(1), 391–396.
Chang, H. C. e C. C. Kuo (1994). Network reconfiguration in distribution systems
using simulated annealing. Electric Power System Research 29, 227–238.
71
72
REFERÊNCIAS BIBLIOGRÁFICAS
Charles, D. L., I. K. Hafeezulla e S. Ravichandran (2005). Distribution network
reconfiguration for loss reduction using ant colony system algorithm. IEEE
Indicon Conference, Chennai, India pp. 619–622.
Cheng, C. S. e D. Shirmohammadi (1995). A three-phase power flow method for
real-time distribution system analysis. IEEE Transactions on Power Systems
10(2), 671–679.
Chiang, H. D. e R. Jeam-Jumeau (1990). Optimal network reconfigurations in distribuition systems: part 2: solution algorithms and numerical results. IEEE
Transactions on Power Delivery, New York 5(3), 1568–1574.
Ching-Tzong, S., C. Chung-Fu e C. Ji-Pyng (2005). Distribution network reconfiguration for loss reduction by ant colony search algorithm. Electric Power Systems
Research (75), 190–199.
Chung-Fu, C. (2008). Reconfiguration and capacitor placement for loss reduction
of distribution system by ant colony search algorithm. IEEE Transaction on
Power System 23(4), 1747–1755.
Civanlar, S., J. J. Grainger e S. S. H. Lee (1988). Distribution feeder reconfiguration
for loss reduction. IEEE Transaction on Power Delivery 3(3), 1217–1223.
Ding, Fei e Kenneth A. Loparo (2012). A simple heuristic method for smart distribution system reconfiguration. Em: Energytech, IEEE Conference.
Dorigo, M., Birattari M. e Stutzle T. (2006). Ant colony optimization. IEEE Computational Inteligence Magazine 1(4), 28–39.
Dorigo, M. e L. M. Gambardella (1997). Ant colony system: A coopetative learning
approach to the travelling salesman problem. IEEE Transactions on Evolutionary Computation 1(1), 1–24.
Dorigo, M. e T. Stutzle (2004). Ant colony optimization. Massachusetts Institute of
Technology - MIT Press.
Dorigo, M., V. Maniezzo e Colorni A. (1991). Positive feedback as a search strategy.
Technical Report 91-016, Dipartimento di Elettronica, Politecnico di Milano,
Italy pp. 1–20.
Huilman Sanca Sanca - Dissertação de Mestrado
REFERÊNCIAS BIBLIOGRÁFICAS
73
Dorigo, M., V. Maniezzo e Colorni A. (1996). Ant system: Optimization by a colony
of cooperating agents. Systems, Man, and Cybernetics, Part B: Cybernetics,
IEEE Transactions 26(1), 29–41.
Eberhart, R. e Yuhui Shi (2001). Particle swarm optimization: Development, application and resources. IEEE Congress on Evolutionary Computation 1, 81–86.
Gambardella, L. M. e M. Dorigo (1995). Ant-q: A reinforcement learning approach to
the travelling salesman problem. Proceedings of ML-95, Twelfth International
Conference on Machine Learning, Tahoe City, CA, A. Prieditis, S. Russell
(Eds.), Morgan Kaufmann pp. 252–260.
Gomes, F. V., J. S. Carneiro, J. L. R. Pereira, M. P. Vinagre, P. A. N. Garcia
e L. R. Araujo (2006). A new distribution system reconfiguration approach
using optimum power flow and sensitivity analysis for loss reduction. IEEE
Transactions on Power System 21(4), 1616–1623.
Guimarães, M. A. N. (2005). Reconfiguração de sistemas de distribuição de energia elétrica utilizando algoritmos de busca tabu. Disertassão (Mestrado em
engenharia elétrica)- Faculdade de Engenharia Elétrica e de Computação, Universidade Estadual de Campinas, Campinas pp. 1–108f.
Haque, M. H. (1996). A general load flow method for distribution systems. Electric
Power System Research 54(1), 47–54.
Hu, X., Y. Shi e R. Eberhart (2004). Recent advances in particle swarm. IEEE
Congress on Evolutionary Computation 1, 90–97.
Jeon, Y., J. C. Kim, J. Kim, J. R. Shin e K.Y. Lee (2002). An efficient simulated
annealing algorithm for network reconfiguration in large-scale distribution systems. IEEE Transactions on Power Delivery 17, 1070–1078.
Kim, H., Y. Ko e K. H. Jung (1993). Artificial neural network based feeder reconfiguration for loss reduction in distribution systems. IEEE Transactions on Power
Delivery, New York. 8(3), 1356–1366.
Lin, W. M., F. S. Cheng e M. T. Tsay (2000). Distribution feeder reconfiguration
with refined genetic algorithm. IEE Procedings Generation, Transmition and
Distribution 147(6), 349–354.
73
74
REFERÊNCIAS BIBLIOGRÁFICAS
Lorenzeti, J. F. C. (2004). Reconfiguração de sistemas de distribuição de energia
elétrica para a melhoria das condições de operação com relação à estabilidade
de tensão. Disertassão (Mestrado em engenharia elétrica)- Faculdade de Engenharia Elétrica e de Computação, Universidade Estadual de Campinas - UNICAMP, Campinas, SP pp. 1–100f.
Lu, L., J. Liu e J. Wang (2009). A distributed hierarchical structure optimization algorithm based poly-particle swarm for reconfiguration of distribution network.
Em: SUPERGEN 09 International Conference on Sustainable Power Generation and Supply.
Mantovani, J. R. S., Casari F. e Romero R. A. (2000). Reconfiguração de sistemas de
distribuição radiais utilizando o critério de queda de tensão. Revista Controle
e Automação, Sociedade Brasileira de Automática, SBA. 11(3), 150–159.
Merlin, A. e H. Back (1975). Search for a minimal-loss operating spanning tree
configuration in an urban power distribution system. In Proceedings 5th Power
System Computation Conference - PSCC, Cambridge, U.K. 1(1), 1–18.
Morelato, A. L. e A. Monticelli (1989). Heuristic search approach to distribution
system restoration. IEEE Transactions an Power Delivery 4(4), 2235–2241.
Nara, K., A. Shiose, M. Kitagawa e T. Ishihara (1992). Implementation of genetic
algorithm for distribution systems loss minimum reconfiguration. IEEE Transaction on Power System 7(3), 1044–1051.
Olamaei, J., Gharehpetian G. e Niknam T. (2007). An approach based on particle swarm optimization for distribution feeder reconfiguration considering distributed generators. Power Systems Conference: Advanced Metering, Protection, Control, Communication, and Distributed Resources - PSC pp. 326–330.
Parada, V., J. A. Ferland, M. Arias e K. Daniels (2004). Optimization of electrical
distribution feeders using simulated annealing. IEEE Transactions on Power
Delivery 19, 1135–1141.
Pereira, F. S., K. Vittori e G. R. M. da Costa (2006). Distribution system reconfiguration for loss reduction based on ant colony behavior. Em: IEEE PES Transaction and Distribution Conference and Exposition Latin America, Venezuela.
Huilman Sanca Sanca - Dissertação de Mestrado
Salazar, H., R. Gallego e R. Romero (2006). Artificial neural networks and clustering techniques applied in the reconfiguration of distribution systems. IEEE
Transactions on Power Delivery, New York. 21(3), 1735–1742.
Shin, D. J., T. K. Kim, J. B. Choo e C. Singh (2004). Optimal service restoration
and reconfiguration of network using genetic-tabu algorithm. Electric Power
Systems Research. 71, 145–152.
Srinivasa, R. e S. V. L. Narasimhan (2009). A new heuristic approach for optimal
network reconfiguration in distribution system. International Journal of Engineering and Applied Sciences 5(1), 15–21.
Stutzle, Thomas e Holger H. Hoos (1996). Improving the ant system: A detailed
report on the max-min ant system. FG Intellektik, FB Informatik, TU Darmstadt, Germany, Tech. Rep. AIDA pp. 1–22.
Stutzle, Thomas e Holger H. Hoos (2000). Max-min ant system. Future Generation
Computer Systems - Elsevier Science 16, 889–914.
Toune, S., H. Fudo, T. Genji, Y. Fukuyama e Y. Nakanishi (1998). A reactive
tabu search for service restoiration in electric power distribution systems. IEEE
International Conference on Evolutionary Computation, Anchorage, Alaska
pp. 4–11.
Zhijiam, H., H. Xixiong amd G. Yang e L. Dong (2008). Distribution network reconfiguration baset on ant colony system algorithm. IEEE Industrial Electronics
and Application, ICIEAalgorithm, Conference pp. 2470–2474.
Zhu, J. Z. (2002). Optimal reconfiguration of electrical distribution network using the refined genetic algorithm. Electric Power Systems Research, Lausanne
62(1), 37–42.
75
76
Apêndice A
Divulgação da Pesquisa
D
URANTE o desenvolvimento deste trabalho e decorrente da pesquisa foram
submetidos os seguintes artigos:
• Sanca, H. S., Ferreira, N. R. e Souza, B. A. ”Reconfiguração de redes de
distribuição de energia elétrica utilizando metaheurı́stica Colônia de formigas
modificada”. X Encontro Anual de Computação - EnAComp, Catalão, Goiás,
Brasil. v. 1, p. 1-8, Fevereiro, 2013 (Apresentado).
• Sanca, H. S., Ferreira, N. R. e Souza, B. A. ”Algoritmo colônia de formigas
com elitismo aplicado à reconfiguração ótima de sistemas de distribuição de
energia elétrica”. Conferência Brasileira sobre Qualidade da Energia Elétrica
- CBQEE, Araxá, Minas Gerais, Brasil. v. 1, p. 1-6, Junho, 2013 (Apresentado).
• Sanca, H. S., Ferreira, N. R. e Souza, B. A. ”Redução de perdas na recon-
figuração de sistemas de distribuição de energia elétrica aplicando MAX-MIN
Ant System”. Simpósio Brasileiro de Automação inteligente - SBAI, Forta-
leza, Ceará, Brasil. v. 1, pp. 1-6, 2013 (Submetido).
77
78
Apêndice B
Dados dos Sistemas Testados
B.1
Sistema de 33 barras
79
Tabela B.1: Dados do sistema de 33 barras.
Ramo
Barra
inicial
Barra
final
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
2
19
20
21
3
23
24
6
26
27
28
29
30
31
32
8
9
12
18
25
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
21
15
22
33
29
Resistência
do ramo
(Ω)
0,0922
0,4930
0,3660
0,3811
0,8190
0,1872
0,7114
1,0300
1,0440
0,1966
0,3744
1,4680
0,5416
0,5910
0,7463
1,2890
0,7320
0,1640
1,5042
0,4095
0,7089
0,4512
0,8980
0,8960
0,2030
0,2842
1,0590
0,8042
0,5075
0,9744
0,3105
0,3410
2,0000
2,0000
2,0000
0,5000
0,5000
Reatância
do ramo
(Ω)
0,0470
0,2511
0,1864
0,1941
0,7070
0,6188
0,2351
0,7400
0,7400
0,0650
0,1238
1,1550
0,7129
0,5260
0,5450
1,7210
0,5740
0,1565
1,3554
0,4784
0,9373
0,3083
0,7091
0,7011
0,1034
0,1447
0,9337
0,7006
0,2585
0,9630
0,3619
0,5302
2,0000
2,0000
2,0000
0,5000
0,5000
80
Potência ativa
barra final
(kW)
100
90
120
60
60
200
200
60
60
45
60
60
120
60
60
60
90
90
90
90
90
90
420
420
60
60
60
120
200
150
210
60
Potência reativa
barra final
(kVar)
60
40
80
30
20
100
100
20
20
30
35
35
80
10
20
20
40
40
40
40
40
50
200
200
25
25
20
70
600
70
100
40
B.2
Sistema de 69 barras
Tabela B.2: Dados do sistema de 69 barras, parte 1 de 2.
Ramo
Barra
inicial
Barra
final
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
3
28
29
30
31
32
33
34
3
36
37
38
39
40
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
Resistência
do ramo
(Ω)
0,0005
0,0005
0,0015
0,0251
0,3660
0,3811
0,0922
0,0493
0,8190
0,1872
0,7114
1,0300
1,0440
1,0580
0,1966
0,3744
0,0047
0,3276
0,2106
0,3416
0,0140
0,1591
0,3463
0,7488
0,3089
0,1732
0,0044
0,0640
0,3978
0,0702
0,3510
0,8390
1,7080
1,4740
0,0044
0,0640
0,1053
0,0304
0,0018
0,7283
Reatância
do ramo
(Ω)
0,0012
0,0012
0,0036
0,0294
0,1864
0,1941
0,0470
0,0251
0,2707
0,0619
0,2351
0,3400
0,3450
0,3496
0,0650
0,1238
0,0016
0,1083
0,0696
0,1129
0,0046
0,0526
0,1145
0,2475
0,1021
0,0572
0,0108
0,1565
0,1315
0,0232
0,1160
0,2816
0,5646
0,4873
0,0108
0,1565
0,1230
0,0355
0,0021
0,8509
81
Potência ativa
barra final
(kW)
0,0
0,0
0,0
0,0
0,87800
13,4550
24,8870
10,0000
9,3330
48,5000
48,5000
2,7100
2,7100
0,0
15,1760
16,5000
16,5000
0,0
0,3160
37,9830
1,7620
0,0
9,3900
0,0
4,6670
4,6670
8,6670
8,6670
0,0
0,0
0,0
4,5820
6,5010
1,9200
8,6670
8,6670
0,0
8,0000
8,0000
0,3920
Potência reativa
barra final
(kVar)
0,0
0,0
0,0
0,0
0,7200
9,9820
17,8100
7,2080
6,6660
34,6090
34,6090
1,8210
1,8210
0,0
10,1980
11,7750
11,7750
0,0
0,2120
27,1000
1,1840
0,0
6,6700
0,0
3,3300
3,3300
6,1850
6,1850
0,0
0,0
0,0
3,2600
4,5490
1,2900
6,1850
6,1850
0,0
5,7090
5,7090
0,3250
Tabela B.3: Dados do sistema de 69 barras, parte 2 de 2.
Ramo
Barra
inicial
Barra
final
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
41
42
43
44
45
4
47
48
49
8
51
9
53
54
55
56
57
58
59
60
61
62
63
64
11
66
12
68
11
13
15
50
27
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
43
21
46
59
65
Resistência
do ramo
(Ω)
0,3100
0,0410
0,0092
0,1089
0,0009
0,0034
0,0851
0,2898
0,0822
0,0928
0,3319
0,1740
0,2030
0,2842
0,2813
1,5900
0,7837
0,3042
0,3861
0,5075
0,9740
1,1450
0,7105
1,0410
0,2012
0,0047
0,7394
0,0047
0,5000
0,5000
1,0000
2,000
1,0000
Reatância
do ramo
(Ω)
0,3623
0,0478
0,0116
0,1373
0,0012
0,0084
0,2083
0,7091
0,2011
0,0473
0,1114
0,0886
0,1034
0,1447
0,1433
0,5337
0,2630
0,1006
0,1172
0,2585
0,0496
0,0738
0,3619
0,5302
0,0611
0,0014
0,2444
0,0016
0,5000
0,5000
1,0000
2,0000
1,0000
82
Potência ativa
barra final
(kW)
0.00
2,0
0,0
3,0760
3,0760
0,0
26,3500
28,2260
128,2260
13,5120
1,2020
1,4490
8,7870
8,0000
0,0
0,0
0,0
0,6670
0,0
414,6670
10,6670
0,0
75,6700
19,6700
6,0000
6,0000
9,3330
9,3330
Potência reativa
barra final
(kVar)
0,0
1,4270
0,0
8,7870
8,7870
0,0
18,8000
91,4920
91,4920
9,4420
0,8940
1,1620
6,3220
5,7080
0,0
0,0
0,0
24,0250
0,0
295,9100
7,6120
0,0
53,8730
13,9120
4,2820
4,2820
6,6600
6,6600
B.3
Sistema de 136 barras
Tabela B.4: Dados do sistema de 136 barras, parte 1 de 4.
Ramo
Barra
inicial
Barra
final
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
21
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
1
2
3
4
5
6
7
7
9
9
11
11
11
14
14
16
1
18
19
20
21
21
23
23
25
26
27
28
29
30
29
32
33
34
32
36
37
36
1
40
2
3
4
5
6
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
Resistência
do ramo
(Ω)
0,33205
0,00188
0,22340
0,09943
0,15571
0,16321
0,11444
0,05675
0,52124
0,10877
0,39803
0,91744
0,11823
0,50228
0,05675
0,29379
0,33205
0,00188
0,22324
0,10881
0,71078
0,18197
0,30326
0,02439
0,04502
0,01876
0,11823
0,02365
0,18954
0,39803
0,05675
0,09477
0,41699
0,11372
0,07566
0,36960
0,26536
0,05675
0,33205
0,11819
Reatância
do ramo
(Ω)
0,76653
0,00433
0,51530
0,22953
0,35945
0,37677
0,26417
0,05666
0,27418
0,10860
0,20937
0,31469
0,11805
0,26421
0,05666
0,15454
0,76653
0,00433
0,51535
0,25118
0,37388
0,42008
0,15952
0,05630
0,10394
0,04331
0,11805
0,02361
0,09970
0,20937
0,05666
0,04985
0,21934
0,05982
0,07555
0,19442
0,13958
0,05660
0,76653
0,27283
83
Potência ativa
barra final
(kW)
0,000
47,780
42,551
87,022
311,310
148,869
238,672
62,299
124,598
140,175
116,813
249,203
291,447
303,720
215,396
198,586
0,000
0,000
0,000
30,127
230,972
60,256
230,972
120,507
0,000
56,981
364,665
0,000
124,647
56,981
0,000
85,473
0,000
396,735
0,000
181,152
242,172
75,316
0,000
1,254
Potência reativa
barra final
(kVar)
0,000
19,009
16,929
34,622
123,855
59,228
94,956
24,786
49,571
55,768
46,474
99,145
115,952
120,835
85,695
79,007
0,000
0,000
0,000
14,729
112,920
29,458
112,920
58,915
0,000
27,857
178,281
0,000
60,939
27,857
0,000
41,787
0,000
193,960
0,000
88,563
118,395
36,821
0,000
0,531
Tabela B.5: Dados do sistema de 136 barras, parte 2 de 4.
Ramo
Barra
inicial
Barra
final
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
41
41
43
44
44
46
47
48
49
50
49
52
53
54
55
53
57
58
59
60
61
48
1
64
65
66
67
68
69
69
71
72
71
74
1
76
77
78
79
80
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
Resistência
do ramo
(Ω)
2,96288
0,00188
0,06941
0,81502
0,06378
0,13132
0,06191
0,11444
0,28374
0,28374
0,04502
0,02626
0,06003
0,03002
0,02064
0,10881
0,25588
0,41699
0,50228
0,33170
0,20849
0,13882
0,00750
0,27014
0,38270
0,33018
0,32830
0,17072
0,55914
0,05816
0,70130
1,02352
0,06754
1,32352
0,01126
0,72976
0,22512
0,20824
0,04690
0,61950
Reatância
do ramo
(Ω)
1,01628
0,00433
0,16024
0,42872
0,14724
0,30315
0,14291
0,26417
0,28331
0,28331
0,10394
0,06063
0,13858
0,06929
0,04764
0,25118
0,13460
0,21934
0,26421
0,17448
0,10967
0,32047
0,01732
0,62362
0,88346
0,76220
0,75787
0,39409
0,29412
0,13425
0,36890
0,53839
0,15591
0,45397
0,02598
1,68464
0,51968
0,48071
0,10827
0,61857
84
Potência ativa
barra final
(kW)
6,274
0,000
117,880
62,668
172,285
458,556
262,962
235,761
0,000
109,215
0,000
72,809
258,473
69,169
21,843
0,000
20,527
150,548
220,687
92,384
0,000
226,693
0,000
294,016
83,015
83,015
103,770
176,408
83,015
217,917
23,294
5,075
72,638
405,990
0,000
100,182
142,523
96,042
300,454
141,238
Potência reativa
barra final
(kVar)
2,660
0,000
49,971
26,566
73,034
194,388
111,473
99,942
0,000
46,298
0,000
30,865
109,570
29,322
9,260
0,000
8,702
63,819
93,552
39,163
0,000
96,098
0,000
116,974
33,028
33,028
41,285
70,184
33,028
86,698
9,267
2,019
28,899
161,523
0,000
42,468
60,417
40,713
127,366
59,873
Tabela B.6: Dados do sistema de 136 barras, parte 3 de 4.
Ramo
Barra
inicial
Barra
final
81
82
82
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
81
82
82
84
1
86
87
87
89
90
91
92
93
94
95
96
94
98
1
100
101
102
102
104
105
106
107
108
109
108
111
112
113
109
115
116
117
105
119
120
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
Resistência
do ramo
(Ω)
0,34049
0,56862
0,10877
0,56862
0,01126
0,41835
0,10499
0,43898
0,07520
0,07692
0,33205
0,08442
0,13320
0,29320
0,21753
0,26482
0,10318
0,13507
0,00938
0,16884
0,11819
2,28608
0,45587
0,69600
0,45774
0,20298
0,21348
0,54967
0,54019
0,04550
0,47385
0,86241
0,56862
0,77711
1,08038
1,09933
0,47385
0,32267
0,14633
0,12382
Reatância
do ramo
(Ω)
0,33998
0,29911
0,10860
0,29911
0,02598
0,96575
0,13641
1,01338
0,02579
0,17756
0,76653
0,19488
0,30748
0,29276
0,21721
0,26443
0,23819
0,31181
0,02165
0,38976
0,27283
0,78414
1,05236
1,60669
1,05669
0,26373
0,27737
0,28914
0,28415
0,05911
0,24926
0,45364
0,29911
0,40878
0,56830
0,57827
0,24926
0,74488
0,33779
0,28583
85
Potência ativa
barra final
(kW)
279,847
87,312
243,849
247,750
0,000
89,878
1137,280
458,339
385,197
0,000
79,608
87,312
0,000
74,001
232,050
141,819
0,000
76,449
0,000
51,322
59,874
9,065
2,092
16,735
1506,522
313,023
79,831
51,322
0,000
202,435
60,823
45,618
0,000
157,070
0,000
250,148
0,000
69,809
32,072
61,084
Potência reativa
barra final
(kVar)
118,631
37,013
103,371
105,025
0,000
38,101
482,108
194,296
163,290
0,000
33,747
37,013
0,000
31,370
98,369
60,119
0,000
32,408
0,000
21,756
25,381
3,843
0,887
7,094
638,634
132,694
33,842
21,756
0,000
85,815
25,874
19,338
0,000
66,584
0,000
106,041
0,000
29,593
13,596
25,894
Tabela B.7: Dados do sistema de 136 barras, parte 4 de 4.
Ramo
Barra
inicial
Barra
final
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
1
122
123
124
124
126
126
128
128
130
131
132
133
134
135
8
10
16
39
26
51
56
63
67
80
85
92
91
91
93
93
97
111
127
129
136
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
74
25
84
136
52
97
99
121
80
132
136
105
130
104
105
133
121
48
77
78
99
Resistência
do ramo
(Ω)
0,01126
0,64910
0,04502
0,52640
0,02064
0,53071
0,09755
0,11819
0,13882
0,04315
0,09192
0,16134
0,37832
0,39724
0,29320
0,13132
0,26536
0,14187
0,08512
0,04502
0,14187
0,14187
0,03940
0,12944
0,01688
0,33170
0,14187
0,07692
0,07692
0,07692
0,07692
0,26482
0,49696
0,17059
0,05253
0,29320
Reatância
do ramo
(Ω)
0,02598
1,49842
0,10394
0,18056
0,04764
0,27917
0,22520
0,27283
0,32047
0,09961
0,21220
0,37244
0,37775
0,39664
0,29276
0,30315
0,13958
0,14166
0,08499
0,10394
0,14166
0,14166
0,09094
0,29882
0,03898
0,17448
0,14166
0,17756
0,17756
0,17756
0,17756
0,26443
0,64567
0,08973
0,12126
0,29276
86
Potência ativa
barra final
(kW)
0,000
94,622
49,858
123,164
78,350
145,475
21,369
74,789
227,926
35,614
249,295
316,722
333,817
249,295
0,000
Potência reativa
barra final
(kVar)
0,000
46,260
24,375
60,214
38,304
71,121
10,447
36,564
111,431
17,411
121,877
154,842
163,199
121,877
0,000