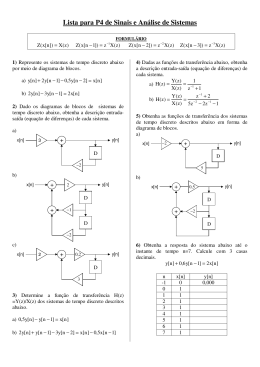
Processamento Digital de Sinais – Aula 3 – Professor Marcio Eisencraft – fevereiro 2012
Aula 3
-
Classificação de sinais
Bibliografia
OPPENHEIM, A.V.; WILLSKY, A. S. Sinais e Sistemas, 2a edição, Pearson, 2010. ISBN 9788576055044.
Páginas 1-20.
HAYKIN, S. S.; VAN VEEN, B. Sinais e sistemas, Bookman, 2001. ISBN 8573077417. Páginas 40-46.
1.6
Classificação de sinais
• Nas aulas anteriores, vimos que um sinal, de forma geral é uma função (contínua ou discreta) do tempo. Veremos agora como podemos classificar os sinais segundo alguns critérios como simetria, periodicidade e energia.
• Em cada caso, veremos as definições para sinais de tempo contínuo e discreto.
1.6.1 Classificação baseada na simetria
1.6.1.1
Sinais de tempo contínuo
• Um sinal de tempo contínuo é dito par se ele satisfizer a condição
x(− t ) = x(t ) , para todo t
• Um sinal de tempo contínuo é dito ímpar se ele satisfizer a condição
x(− t ) = − x(t ) , para todo t
• Assim, os sinais pares são simétricos com relação ao eixo vertical ou origem
dos tempos enquanto que os sinais ímpares são antisimétricos em relação à
origem dos tempos.
• Os sinais x(t ) = t 2 e x(t ) = t 3 são exemplos de sinal par e ímpar respectivamente. O gráfico destes sinais está mostrado a seguir.
1
Processamento Digital de Sinais – Aula 3 – Professor Marcio Eisencraft – fevereiro 2012
• Qualquer sinal x(t ) pode ser decomposto numa soma de dois outros sinais, um
par x p (t ) e outro ímpar xi (t ) , ou seja,
x(t ) = x p (t ) + xi (t ) , (1)
com x p (− t ) = x p (t ) e
xi (− t ) = − xi (t )
• Trocando t por − t na expressão (1), temos:
x(− t ) = x p (− t ) + xi (− t ) = x p (t ) − xi (t ) (2)
• Resolvendo o sistema (1)-(2) para x p (t ) e xi (t ) , chega-se a:
1
xp ( t ) = ( x( t ) +x( −t ) )
2
1
xi ( t ) = ( x( t ) −x( −t ) )
2
1.6.1.2
Sinais de tempo discreto
• De forma análoga ao que foi feito em tempo contínuo, definimos sinais de
tempo discreto par e ímpar como:
Sinal par:
x[− n] = x[n] , para todo n .
Sinal ímpar:
x[− n] = − x[n] , para todo n .
• Demonstra-se também, de forma análoga ao que foi feito antes, que qualquer
sinal pode ser decomposto em uma componente par e numa componente ímpar.
x p [n ] =
1
(x[n ] + x[− n ])
2
1
xi [n ] = ( x[n ] − x[− n ])
2
• A figura seguinte mostra exemplos de sinais de tempo discreto par e ímpar.
2
Processamento Digital de Sinais – Aula 3 – Professor Marcio Eisencraft – fevereiro 2012
Exercícios
1. (MITRA, 2001; p.106) Determine a componente par e ímpar das sequências a
seguir definidas no intervalo − 3 ≤ n ≤ 3 :
(a) x[n] = {3; − 2; 0; 1; 4; 5; 2}
(b) y[n] = {0; 7; 1; − 3; 4; 9; − 2}
(c) w[n] = {− 5; 4; 3; 6; − 5; 0; 1}
1.6.2 Classificação quanto à periodicidade
1.6.2.1 Sinais de tempo contínuo
• Um sinal x(t ) é dito periódico quando satisfizer a condição x(t ) = x(t + T ) para
todo t e T é uma constante positiva.
• O menor valor de T que satisfaz esta condição é chamado de período fundamental de x(t ) .
• O inverso do período fundamental é a frequência fundamental, que, quando o
período é medido em segundos, é dada em Hertz (Hz).
f =
1
T
• Também definimos a frequência angular do sinal, medida em radianos por
segundo como:
3
Processamento Digital de Sinais – Aula 3 – Professor Marcio Eisencraft – fevereiro 2012
Ω=
2π
T
• Quando o sinal não apresenta um período mínimo T é chamado de aperiódico.
Exercício
2. (HAYKIN, 2000; p. 37) A figura a seguir mostra uma onda triangular. Qual é
a frequência fundamental desta onda? Expresse a frequência fundamental em
unidades de Hz ou rad/s.
1.2.2.2
Sinais de tempo discreto
• A classificação de sinais em sinais periódicos e aperiódicos apresentada até
agora se aplica a sinais de tempo contínuo. Consideraremos a seguir o caso de
sinais de tempo discreto.
• Diz-se que um sinal de tempo discreto x[n] é periódico se ele satisfizer a condição
x[n] = x[n + N ],
para todos os números inteiros n e N um número inteiro positivo.
4
Processamento Digital de Sinais – Aula 3 – Professor Marcio Eisencraft – fevereiro 2012
• O menor valor de N que satisfaz a definição anterior é chamado de período
fundamental do sinal de tempo discreto x[n] . A frequência angular fundamental ou, simplesmente, frequência fundamental de x[n] é definida por:
ω=
2π
N ,
que é medida em radianos.
• Lembre-se: O período de um sinal de tempo discreto é obrigatoriamente um
número inteiro. Assim, sua frequência angular fundamental ω não pode assumir qualquer valor.
Exercício
3. (HAYKIN, 2000; p. 78) Determine se os seguintes sinais são periódicos. Se
forem periódicos, encontre o período fundamental.
(a) x[n] = (− 1)n
(b) x[n] descrito na figura a seguir.
1.6.3 Sinais de energia e potência
1.6.3.1
Sinais de tempo contínuo
• Em sistemas elétricos, um sinal pode representar uma tensão ou uma corrente.
Considere uma tensão v(t ) aplicada a um resistor de resistência R , produzindo
uma corrente i(t ) . A potência instantânea dissipada no resistor é definida por
5
Processamento Digital de Sinais – Aula 3 – Professor Marcio Eisencraft – fevereiro 2012
v 2 (t )
2
p(t ) =
ou p (t ) = Ri (t ) .
R
• Vemos assim que a potência instantânea p(t ) é proporcional à amplitude do
sinal elevada ao quadrado. Além do mais, para R = 1Ω , vemos que a potência
p(t ) é exatamente igual à amplitude ao quadrado do sinal.
• Baseado nisso, em análise de sinais, costuma-se definir a potência instantânea
de um sinal x(t ) como:
p(t ) = x 2 (t ) .
• Lembrando que a energia é o produto da potência pelo tempo, costuma-se definir a energia total do sinal x(t ) como:
Ex = lim
T →∞
∫
T
2
−T
2
x
2
( t )dt
=
∞
∫−∞
x 2 ( t )dt
.
• Também definimos a potência média de um sinal x ( t ) como
1
Px = lim
T →∞ T
∫
T
2
−T
2
x 2 ( t )dt
.
• Para sinais periódicos, podemos calcular a potência média tomando a média
apenas num período ao invés de tomar todo o eixo dos tempos. Para um sinal
x ( t ) periódico de período fundamental T , temos:
1
Px =
T
∫
T
2
−T
2
x 2 ( t )dt
.
• A raiz quadrada da potência média Px é chamada de valor médio quadrático
(RMS – Root-Mean-Square) do sinal x(t ) .
6
Processamento Digital de Sinais – Aula 3 – Professor Marcio Eisencraft – fevereiro 2012
1.6.3.2
Sinais de tempo discreto
• No caso de um sinal de tempo discreto x[n] , as integrais anteriores são substituídas pelas somas correspondentes. Dessa forma, a energia total de x[n] é definida por:
∞
Ex =
∑
n =−∞
x 2  n 
e sua potência média é definida por:
N
1
Px = lim
x 2  n  .
∑
N →∞ 2N + 1
n =−N
• Novamente, para um sinal periódico, basta tomarmos a média de um período
para o cálculo da potência média. Assim, para o caso de um sinal x[n] com período fundamental N ,
1
Px =
N
N −1
∑ x 2  n  .
n =0
• Um sinal é chamado de sinal de energia se e somente se a energia total do
sinal satisfizer a condição
0 < Ex < ∞ .
• Um sinal é chamado de sinal de potência se e somente se a potência média do
sinal satisfizer a condição
0 < Px < ∞ .
• Pode-se mostrar que as classificações de energia e potência de sinais são mutuamente exclusivas. Em especial, um sinal de energia tem potência média zero enquanto que um sinal de potência tem energia infinita.
7
Processamento Digital de Sinais – Aula 3 – Professor Marcio Eisencraft – fevereiro 2012
Exercícios
4. (HAYKIN, 2000; p. 39) Qual a energia total do pulso retangular mostrado na
figura a seguir?
Resposta:
A 2T1
5. (HAYKIN, 2000; p. 39) Qual é a potência média da onda quadrada mostrada
na figura a seguir?
Resposta: 1
6. (HAYKIN, 2000; p. 40) Qual é a potência média da onda triangular mostrada
a seguir?
Resposta: 1/3
7. (HAYKIN, 2000; p. 40) Qual a energia total do sinal de tempo discreto mostrado a seguir?
8
Processamento Digital de Sinais – Aula 3 – Professor Marcio Eisencraft – fevereiro 2012
8. (HAYKIN, 2000; p. 40) Qual a potência média do sinal periódico de tempo
discreto mostrado na figura a seguir?
9