Programação para as Ciências Experimentais – 05/06
Exercícios de Programação (Octave)
1. Escrever uma função que, utilizando o algoritmo de Euclides, determine o maior divisor
comum de dois números inteiros, mdc(m,n).
Ficheiro “mdc.m”:
function resultado=mdc(m,n)
(...)
endfunction
Para usar, no octave fazer:
>> mdc(18,12)
ans=6
2. Escrever uma função para determinar o menor múltiplo comum de dois números
inteiros, mmc(m,n). Utilizar a fórmula:
m×n
mmc=
mdc m , n
3. Escrever uma função que determine um valor aproximado do seno de x ( assuma-se

). Utilizar a fórmula:
x
2
seno(x) = x – x3/3! + x5/5! – x7/7! + x9/9! - ...
Como critério de paragem considere-se a situação em que o termo xi/i! seja inferior a
0.1% da soma acumulada.
4. Escrever uma função que calcule o valor de fibonacci, fib(n). A função fib(n) define-se
para n∈ℕ0 :
1
⇐ n=0
fibn=
fibn−2 fibn−1 ⇐ n0
{
5. À razão entre fib(n) e fib(n-1) é chamado o número de ouro. Escrever uma função 'ouro
(p)' que calcule este número com uma precisão p, i.e que avalia fib(n) para n∈ℕ0 até
que ∣ouro n−ouro n−1∣≤ p .
6. Escreva uma função zero(min,max,p) que determine o zero da função
x
f  x=2 x 2log   com uma precisão p. O algoritmo assume que f é contínua e
4
tem um zero entre min e max.
7. Escreva uma função raiz2(x,p) que calcula a raíz quadrada de um número x com uma
precisão p. Assuma x1 .
8. Considere um vector v de N posições com números aleatórios. Fazer uma função max_v
(v) que determine: a) Qual a posição (índice) do maior elemento do vector. b) Qual é
esse elemento.
9. Considere uma matriz M ×N com números aleatórios. Fazer uma função que calcule:
a) O índice da coluna com a maior soma dos seus elementos. b) Qual é essa soma.
10.Dado um número inteiro, determinar se ele é primo testando se existe um inteiro Q tal
que N =P ×Q para qualquer P=[2,  N ] .
2
11.Dada a função g  x=2 xe−x , fazer uma função integ(min,max,passo) que determine
a sua área entre os limites min e max, através da aproximação por rectângulos ou
trapézios de comprimento g(x) e largura igual ao passo.
Para testar a implementação saiba-se que o valor do integral da função g(x) é dado por :
max
max
∫min g  x=∫min 2 xe−x =e−min −e−max
2
2
2
que no intervalo [0,1] tem o valor 0.632121.
12.O objectivo é simular um passeio aleatório. A função passeio(d) a implementar pretende
determinar quantos passos aleatórios são necessários até atingir uma distância d do ponto
de partida. Partindo-se da posição 0, em cada unidade de tempo é dado um passo
aleatório para a direita (+1) ou para a esquerda (-1) até se atingir a posição +d ou –d.
13.Resolver o exercício 11 utilizando o método de Monte Carlo. A função integ_mc
(min,max,npontos) deverá gerar npontos pontos aleatórios dentro do rectângulo x=
[min,max] e y=[0,1] (considere min>=0 e max <=1). Sabendo-se que a g(x)<1 no
intervalo [0,1] então, para um número suficiente de testes, a percentagem de pontos que
ficaram dentro da área da função pode ser utilizada para aproximar a sua área.
Introdução aos Computadores e Programação – 04/05
Exercícios de Programação (Octave)
(Resolução)
1. Para calcularmos o máximo divisor comum de dois números p e q, utilizamos um
algoritmo cíclico (iterativo). Cada ciclo utiliza os valores de p e q calculados no ciclo
anterior para actualizar q ou p com a diferença entre eles (linha 4 e 6) . O algoritmo
termina quando p e q são iguais (linha 2).
1. function r = mdc(p,q)
2.
while p != q
3.
if q > p
4.
q = q-p;
5.
else
6.
p = p-q;
7.
endif
8.
endwhile
9.
r = p;
10.endfunction
2. Esta função é bastante simples, bastando passar a fórmula dada no enunciado para
octave. Note-se que podemos (e devemos) utilizar a função mdc definida anteriormente.
1. function r = mmc(m,n)
2.
r = m*n/mdc(m,n)
3. endfunction
3. A formula apresentada traduz que o seno de um número pode ser dado por uma soma
xi
com um número arbitrário de termos t i=
. Este exercício é resolvido
i!
iterativamente, em que em cada ciclo adicionamos a uma variável r um novo termo t
(linha 11). Quanto mais termos adicionarmos mais preciso é o valor do seno, portanto o
número de ciclos a fazer vai depender da precisão pretendida (linha 7).
Como o sinal do termo que adicionamos vai alternando (vêr fórmula), podemos utilizar a
seguinte expressão para o i'ésimo termo
t i=−1i ×
x 2 i1
2 i1!
1. function r = seno(x)
2.
r=0;
3.
n=0;
4.
indice=0;
5.
termo=0;
6.
r=0;
7.
x=mod(x,2*pi);
8.
while (termo >= 0.001*r)
9.
indice=2*n+1;
10.
sinal = -1^n;
11.
termo = (x^indice)/fact(indice)
12.
r=r+sinal*termo;
13.
n=n+1;
14.
endwhile
15.endfunction
4. Versão iterativa (cíclica):
Em cada ciclo calculamos o novo valor de fibonnaci utilizando o último e o penúltimo valor
calculados nos ciclos anteriores. Para isso precisamos de duas variáveis que guardam
respectivamente o valor do último ciclo (r) e o valor do penúltimo ciclo (r_anterior).
1. function r = fib_ite(n)
2. r_anterior = 1;
3. r = 1;
4. for ciclo = 2:n
5.
a = r;
6.
r = r + r_anterior;
7.
r_anterior = a;
8. endfor
9. endfunction
Versão recursiva (a função chama-se a si própria):
É basicamente a transcrição para octave da função fib(n), tal como aparece definida
formalmente no enunciado.
1. function r = fib_rec(n)
2. if n<=1
3.
r = 1;
4. else
5.
r = fib_rec(n-1) + fib_rec(n-2);
6. endif
7. endfunction
5. Em cada ciclo actualizamos o número de ouro do ciclo actual e do ciclo anterior,
respectivamente r e r_anterior. Precisamos também de manter uma variável nciclo que
nos diz qual o número do ciclo actual, para que possamos calular o número de fibonacci
respectivo. Para definir a condição de paragem precisamos da função módulo que no
octave se chama abs.
1. function r = ouro(p)
2. nciclo = 2;
3. r_anterior = fib(1) / fib(0);
4. r = fib(nciclo) / fib(nciclo-1);
5. while (abs(r-r_anterior) > p)
6.
r_anterior = r;
7.
nciclo = nciclo + 1;
8.
r = fib(nciclo) / fib(nciclo – 1);
9. endwhile
10.endfunction
6. Primeiro definimos a função f (num ficheiro à parte f.m):
1. function r= f(x)
2. r=2*x^2 + log(x/4)
3. endfunction
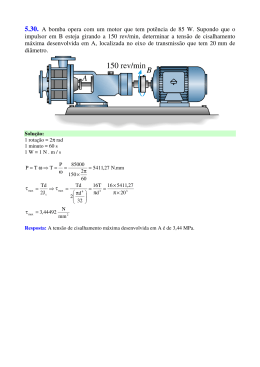
O algoritmo para calcular o zero da função
admite que, entre min e max, ela é contínua e
contém apenas um zero, o que é verdade por
exemplo para min=0 e max=1 (vêr gráfico).
Para descobrir o zero da função vamos
aproximando o intervalo inicial [min,max] tendo
atenção que não excluímos o zero do intervalo, ou seja, o sinal de f(min) tem que ser
diferente do sinal de f(max). O método que utilizamos para ir 'encolhendo' o intervalo é ir
sempre dividindo-o ao meio (e daí o cálculo do parâmetro r), que a maneira que
probabilisticamente nos garante o menor número de ciclos necessários.
1. function r = zero(min,max,p)
2. while max-min > p
3.
r = (max+min)/2;
4.
if f(r)*f(min) < 0
5.
max = r;
6.
else
7.
min = r;
8.
endif
9.
r = (max+min)/2;
10.endwhile;
11.endfunction
7. A raiz quadrada pode ser calculada iterativamente por reduções sucessivas de um
intervalo, tal como fizemos no exercício anterior. Para isso baseamos-nos no facto que
z=  x ⇔ z² = x ⇔ z=
e que
z 1=
x
z
x1 é pressuposto do enunciado. A ideia é utilizar a relação
x
z2
e ir aproximado z1 de z2 até a diferença entre eles ser menor que a precisão p que
pretendemos. Existem várias maneiras de ir actualizando os valores z1 e z1, a que
utilizámos aqui divide o intervalo ao meio, tal como no exercício anterior.
1. function r = raiz2(x,p)
2.
z1 = 1;
3.
z2 = x;
4.
while abs(z2-z1) > p
5.
z1 = (z1+z2)/2;
6.
z2 = x/z1;
7.
endwhile
8.
r = z1;
9. endfunction
8. Para calcularmos qual o máximo elemento de um vector temos que o percorrer todo e ir
guardando o maior elemento encontrado até ao momento - para isso precisamos da
variável maior. Precisamos também de uma variável que guarde o índice do último
maior valor encontrado – a variável ind. No fim retornamos as duas numa matriz linha
com dois elementos.
1. function [maior,indice] = max_v(X)
2.
l = length(X);
3.
indice = 1;
4.
maior = X(1);
5.
for i = 2:l
6.
if X(i) > maior
7.
indice = i;
8.
maior = X(i);
9.
endif;
10.
endfor;
11.endfunction
9. O algoritmo que resolve este problema é bastante semelhante ao do problema anterior,
mas aqui percorremos a matriz iterando coluna a coluna. Para cada coluna calculamos a
sua soma e guardamos esse valor caso seja o maior encontrado até ao momento. O índice
é actualizado tal como no exercício anterior.
1. function [maior,indice] = maxcol(X);
2.
colunas = columns(X);
3.
indice = 1;
4.
maior = sum(X(:,1));
5.
for j = 2:colunas
6.
soma = sum(X(:,j));
7.
if soma > maior
8.
indice = j;
9.
maior = soma;
10.
endif;
11.
endfor;
12.endfunction
10.Para sabermos se um número N é primo testamos a divisão de N por todos os inteiros do
intervalo [2,  N ] . Se a divisão der resto de zero para algum inteiro do intervalo,
então ficamos a saber que o número não é primo, e a função retorna false. Se não
descobrirmos nenhum inteiro do intervalo em que a divisão dá resto de zero então o
número é primo, e a função retorna true.
Para testarmos se uma divisão de a por b dá ou não resto de zero podemos utilizar a
expressão: mod(a,b) == 0.
1. function p = primo(N);
2.
p = true;
3.
lim = sqrt(N);
4.
for i = 2:lim
5.
if mod(N,i) == 0
6.
p = false;
7.
return
8.
endif
9.
endfor;
10.endfunction;
11.Primeiro definimos a função g (num ficheiro à parte g.m):
1. function r= g(x)
2. r=2*x*e^(-x^2)
3. endfunction
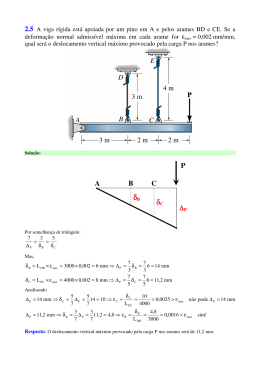
Observe-se o gráfico da função g (a
vermelho). O que se pretende é determinar
a área da função através do uso de
rectângulos (a verde), entre um limite
inferior e superior (neste exemplo 0 e 1).
O número de rectângulos depende do
passo (no exemplo o passo é 0.1). A
largura de cada rectângulo é portanto igual
a passo e a sua altura ao valor dado pela
função g(x) avaliada no ponto médio da
largura do rectângulo.
1. function r = integ(minimo,maximo,passo)
2.
r=0;
3.
for i = minimo+passo/2:passo:maximo
4.
r=r + passo * g(i);
5.
endfor
6. endfunction
12. Precisamos de uma variável pos_actual, inicialmente a 0, para guardar a nossa posição
ao longo dos vários ciclos que terminam quando ∣pos actual∣=d .
Em cada ciclo geramos um número aleatório, e caso seja menor ou maior que 0.5 damos
um passo em direcções diferentes, i.e. somamos ou subtraímos uma unidade à nossa
posição actual (linhas 5-9). A variável npassos guarda o número de passos (ciclos) feitos
até ao momento e é actualizada em cada ciclo (linha 10)
1. function npassos = passeio(d)
2.
pos_actual = 0;
3.
npassos = 0;
4.
while abs(pos_actual) < d
5.
if rand() <= 0.5
6.
pos_actual = pos_actual + 1;
7.
else
8.
pos_actual = pos_actual - 1;
9.
endif
10.
npassos = npassos + 1;
11.
endwhile
12.endfunction
13.Precisamos de gerar npontos pontos aleatórios dentro do rectângulo x=
[minimo,maximo], y=[0,1] (linhas 5 e 6) e contar a percentagem de pontos (px,py) que
calham dentro da função, i.e, py<=g(px), (linhas 7-9). No final essa percentagem é
multiplicada pela área total do rectângulo (linha 11).
1. function r = integ(minimo,maximo,npontos)
2.
pontos_dentro=0;
3.
largura_rect = maximo-minimo;
4.
for i = 1:npontos
5.
px = minimo+rand()*largura_rect;
6.
py = rand();
7.
if py <= g(px)
8.
pontos_dentro = pontos_dentro + 1;
9.
endif
10.
endfor
11.
r = largura_rect * pontos_dentro / npontos;
12.endfunction