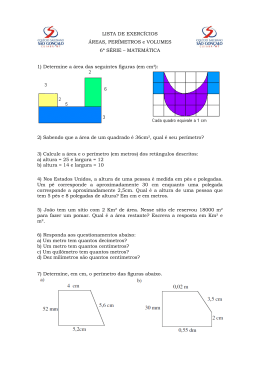
▼
Questão 25
Com o fenômeno do efeito estufa e conseqüente aumento da temperatura média da Terra, há o desprendimento de icebergs (enormes blocos de gelo) das calotas polares terrestres. Para calcularmos o volume aproximado
de um iceberg podemos compará-lo com sólidos geométricos conhecidos. Suponha que o sólido da figura,
formado por dois troncos de pirâmides regulares de base quadrada simétricos e justapostos pela base maior,
represente aproximadamente um iceberg.
30 dam
12 dam
40 dam
As arestas das bases maior e menor de cada tronco medem, respectivamente, 40 dam e 30 dam e a altura mede
12 dam. Sabendo que o volume VS da parte submersa do iceberg corresponde a aproximadamente 7/8 do
volume total V, determine VS.
Resolução
Na figura, cotada em dam, está representado um dos troncos que formam o iceberg.
V
O’... centro do quadrado
de lado 30;
O... centro do quadrado
de lado 40;
A’B’ = 30 e AB = 40.
h
H
A’
O’
B’
12
O
A
B
Temos:
VO’ A’ B’
h
30
=
∴
=
∴ h = 36 e H = 36 + 12 = 48
VO
AB
h + 12 40
O volume VT do tronco, em dam3, pode ser obtido pela diferença entre o volume da pirâmide regular de base
quadrada com altura 48 dam e o volume da pirâmide regular de base quadrada com altura 36 dam. Logo:
VT =
1
1
⋅ 402 ⋅ 48 – ⋅ 302 ⋅ 36 ∴ VT = 14800
3
3
Assim, o volume total V do iceberg, em dm3, é tal que V = 2 ⋅ 14 800, ou seja, V = 29 600.
7
7
Do enunciado, o volume VS, em dam3, é tal que VS =
⋅ V. Logo, VS = ⋅ 29 600, ou seja, VS = 25 900.
8
8
Resposta: 25 900 dam3
1