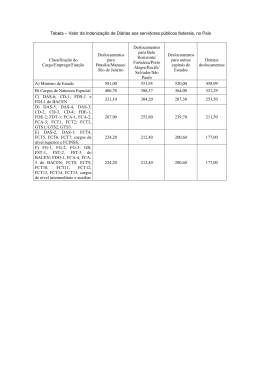
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Introdução ao Método dos Elementos Finitos:
Elasticidade Plana e Tridimensional
1. Introdução
Este texto resume a aplicação do elemento de deslocamento do Método dos Elementos Finitos na
solução de problemas de elasticidade plana e tridimensional.
Começa-se por definir as hipóteses da análise física e geometricamente linear, e recordar as
situações em que se pode admitir que corpos elásticos têm comportamento plano. É este o tipo de
comportamento utilizado na apresentação e interpretação do Método dos Elementos Finitos, o
qual é posteriormente generalizado para a análise de sólidos elásticos.
Definem-se as variáveis necessárias para caracterizar o problema e as equações que simulam
o comportamento da estrutura, recorrendo-se a um exemplo simples para ilustrar a identificação
das variáveis e a função de cada uma das equações, as quais são organizadas de forma idêntica às
da modelação do comportamento de peças lineares: as condições de equilíbrio e de
compatibilidade, no domínio e na fronteira da peça, e as relações de elasticidade.
O exemplo de aplicação é também usado para mostrar que a solução exacta dessas equações
não tem expressão analítica, na maioria das aplicações. Introduz-se, por isso, a ideia básica da
formulação do Método dos Elementos Finitos aqui adoptada, de aproximar o campo de
deslocamentos. Descreve-se depois, sumariamente, a generalização para o caso plano da
formulação anteriormente desenvolvida para a análise de peças lineares.
Essa generalização é ilustrada com um exemplo de introdução, o qual é utilizado para
formular e analisar os critérios de aproximação do campo de deslocamento e a consequente
aproximação do campo de deformações, de modo a assegurar a condição central de obter
soluções aproximadas cinematicamente admissíveis. A aproximação que se obtém para o campo
de tensões aplicando as relações de elasticidade é utilizada para mostrar que não é possível, em
1
Análise de Estruturas II: Elasticidade Plana e Tridimensional
geral, satisfazer localmente as condições de equilíbrio, tanto no domínio como na fronteira do
elemento. O conceito de força nodal equivalente é depois generalizado e utilizado para formular
a equação resolvente do Método dos Elementos Finitos, cuja interpretação é análoga à obtida
para peças lineares: define o equilíbrio nodal dos elementos da malha, combinando as forças
nodais devidas aos deslocamentos nodais (os termos da matriz de rigidez do elemento) e
resultante das forças nodais equivalentes às forças aplicadas, designadamente as forças de massa
e as forças de fronteira do elemento.
Estes conceitos são depois gradualmente generalizados. Começa-se por definir os elementos
mais simples usados na análise de estados planos e usam-se esses resultados para generalizar a
formulação do Método dos Elementos Finitos. As dificuldades de implementação do exemplo
usado para ilustrar essa generalização são depois usadas para justificar a formulação dos
elementos isoparamétricos, correntemente utilizados nos programas comerciais.
A grande vantagem destes elementos é permitirem generalizar, de uma maneira
computacionalmente muito eficaz, a representação da geometria da peça em análise e a
formulação de elementos com diferentes graus de aproximação do campo de deslocamentos.
Para além de demonstrar as vantagens alcançadas com o desenvolvimento de elementos
isoparamétricos, o objectivo principal do texto é o de realçar e fundamentar os cuidados a ter na
sua utilização. Dá-se particular atenção à análise da adequabilidade das malhas de discretização
que suportam a utilização desses elementos na análise de problemas bidimensionais.
Concluída a apresentação e a ilustração dos principais conceitos que suportam a aplicação do
Método dos Elementos Finitos na análise de problemas de elasticidade plana, sistematiza-se a
generalização da formulação para a análise de problemas tridimensionais. Como essa
generalização não exige a introdução de novos conceitos, o texto incide fundamentalmente na
identificação das variáveis e das equações que as relacionam, e na técnica usada para discretizar
a geometria do sólido em análise e para aproximar os campos de deslocamento, deformação e
tensão. Generaliza-se o conceito de elemento isoparamétrico e comenta-se brevemente o
processo utilizado na montagem da equação resolvente do Método dos Elementos Finitos.
Como a sistematização da aplicação do método é análoga à anteriormente descrita na sua
aplicação de estruturas articuladas e reticuladas, opta-se aqui por analisar as diferentes fases que
caracterizam a utilização de um programa de elementos finitos, dando-se especial atenção às
fases que dependem da intervenção directa do utilizador, ou seja a definição dos dados, a
avaliação da qualidade da malha de discretização gerada automaticamente e, principalmente, à
análise crítica dos resultados obtidos.
2
Análise de Estruturas II: Elasticidade Plana e Tridimensional
2. Hipóteses
Na extensão da aplicação do Método dos Elementos Finitos para análise de problemas de
elasticidade plana e tridimensional continua-se a admitir que o material é elástico linear
(linearidade física) e que os deslocamentos e as deformações são infinitesimais (linearidade
geométrica). Continua-se também a admitir que são desprezáveis as forças de inércia e de
amortecimento que se possam desenvolver durante o carregamento da estrutura (comportamento
quase-estático).
Relativamente à geometria da peça e a forma como é solicitada, consideram-se dois tipos de
problemas que podem ser adequadamente modelados recorrendo à formulação bidimensional da
Teoria da Elasticidade, designadamente, o comportamento de peças sujeitas a estados planos de
tensão ou a estados planos de deformação.
Uma placa é uma peça laminar plana solicitada no próprio plano, com uma espessura
suficientemente pequena em relação às restantes dimensões características para justificar a
hipótese de serem desprezáveis as componentes correspondentes do tensor das tensões. Esta
hipótese é frequentemente utilizada na análise de paredes resistentes.
Se, pelo contrário, a peça é prismática com uma espessura muito maior que as dimensões da
sua secção transversal, em cujo plano actuam as cargas, torna-se legítimo assumir que as secções
se deformam no próprio plano, sendo desprezáveis as três componentes do tensor das
deformações relativas à dimensão transversal. Esta é a hipótese adoptada, por exemplo, na
análise de muros de suporte e de secções de túneis.
y
y
y
Lx
Γ
Lz
Γ
Ω
Ly
x
z
V
x
EPT : Lz ≪ Lx ≈ Ly
EPD : Lz ≫ Lx ≈ Ly
x
z
E3D : Lx ≈ Ly ≈ Lz
Figura 1: Problemas de Elasticidade Plana e Tridimensional
Como se ilustra na Figura 1, o elemento estrutural é representado no plano em que actuam as
cargas, o qual corresponde ao plano médio da placa, num estado plano de tensão (EPT), ou a
3
Análise de Estruturas II: Elasticidade Plana e Tridimensional
secção transversal da peça prismática, num estado plano de deformação (EPD). A área ocupada
pela peça define o domínio, Ω , e a linha que a limita define a fronteira, Γ .
Quando as dimensões características da peça são da mesma ordem, ou quando o tipo de acção
torna inadequadas as hipóteses simplificativas sobre o estado de tensão ou de deformação, a peça
é analisada recorrendo à formulação tridimensional da Teoria da Elasticidade. O volume
ocupado pela peça define o domínio, Ω , e a superfície que a limita define a fronteira, Γ .
Para simplificar a apresentação, a aplicação do Método dos Elementos Finitos a problemas de
elasticidade é feita tratando primeiro a análise de estados planos, estabelecendo-se depois a
generalização da formulação para a análise de problemas tridimensionais.
3. Variáveis
Em consequência das hipóteses que caracterizam os estados planos de tensão e de deformação, e
de acordo com a notação definida nas Figuras 1 e 2, o estado de tensão em cada ponto da peça é
definido por três componentes do tensor das tensões (simétrico), as quais são organizadas
matricialmente na forma,
 σ xx 


s =  σ yy 
σ 
 xy 
(1)
sendo nulas as restantes componentes nos estados planos de tensão: σ xz = σ yz = σ zz = 0 .
y
y
ty , uy
tx , ux
σ yy , ε yy
f y , uy
σ xy , γ xy
σ xx , ε xx
f x , ux
x
x
Figura 2: Convenção adoptada na medição de variáveis
O estado de deformação é definido pelas três componentes correspondentes do tensor das
deformações (simétrico), as quais são organizadas matricialmente de forma análoga,
 ε xx 
 
e =  ε yy 
γ 
 xy 
4
(2)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
em que γ xy = 2ε xy representa a distorção total. As restantes componentes são nulas nos estados
planos de deformação: γ xz = γ yz = ε zz = 0 .
Relativamente às forças aplicadas, distinguem-se as forças de domínio ou de massa
(equivalentes às cargas de vão das barras),
 fx 
f = 
 fy 
(3)
e as forças de fronteira (equivalentes às forças de extremidade):
 tx 
t = 
ty 
As forças de domínio podem ser distribuídas, na área ou em linha, ou concentradas, e as
forças de fronteira distribuídas ou concentradas. Os deslocamentos correspondentes são
organizados de modo análogo:
 ux 
u= 
uy 
(4)
Variáveis estáticas
Variáveis cinemáticas
Tensões, σ ij ( x, y )
Deformações, ε ij ( x, y )
Forças, f i ( x, y ), ti ( x, y )
Deslocamentos, ui ( x, y )
Quadro 1: Variáveis correspondentes
Admite-se, em geral, que não existem momentos aplicados no plano do carregamento, mz = 0
no domínio e na fronteira. A rotação correspondente é uma variável dependente, podendo ser
determinada a partir do campo de deslocamentos:
ω z = − 12 ( ∂ y u x − ∂ x u y )
(5)
4. Balanço Energético
De acordo com a notação anteriormente definida, são as seguintes as definições do trabalho
realizado pelas forças interiores e exteriores:
Wi = ∫ e T s d Ω = ∫ (ε xxσ xx + ε yyσ yy + γ xyσ xy ) d Ω
Ω
Ω
We = ∫ uT f d Ω + ∫ uT t d Γ = ∫ (u x f x + u y f y ) d Ω + ∫ (u x t x + u y t y ) d Γ
Ω
Γ
Ω
Γ
(6)
A condição de balanço energético toma agora a seguinte forma:
∫Ω e
T
s d Ω = ∫ uT f d Ω + ∫ uT t d Γ
Ω
Γ
5
(7)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
y
y
Fy , u y
Fx , u x
Fy , u y
Γℓ
Fx , u x
f ℓ , uℓ
x
x
Figura 3: Forças descontínuas e deslocamentos correspondentes
A definição (6) mantém-se válida quando se pretende calcular o trabalho realizado por forças
de domínio distribuídas ao longo de linhas e de forças de domínio e de fronteira concentradas,
representando essas forças através de funções de Dirac. Na definição explícita que se obtém,
We = ∫ uT f d Ω + ∫ uT t d Γ + ∫ uT f ℓ d Γ ℓ + uT F
Ω
Γ
Γℓ
f ℓ é a força distribuída aplicada sobre a linha Γ ℓ e F o vector que lista as forças concentradas.
O vector u define, no primeiro caso, as componentes do deslocamento ao longo da linha Γ ℓ e,
no segundo, as componentes do deslocamento correspondentes às forças concentradas, como se
ilustra na Figura 3.
5. Equações Básicas
As equações que caracterizam um problema de Elasticidade Plana estão resumidas no Quadro 2,
analisando-se em seguida o significado das condições de domínio (8) a (10) e das condições de
fronteira (11) e (12).
Equilíbrio
Elasticidade
Compatibilidade
Domínio (8)
Domínio (9)
Domínio (10)
AT s + f = 0 em Ω
s = D e em Ω
e = A u em Ω
N Ts = t
u = u em Γ u
em Γ t
Fronteira (11)
Fronteira (12)
Quadro 2: Equações básicas
Estas equações são a seguir escritas explicitamente, sublinhando-se o significado das
condições físicas que impõem. Dá-se particular atenção às condições de fronteira, pois são
6
Análise de Estruturas II: Elasticidade Plana e Tridimensional
aquelas que mais directamente prestam informação sobre a qualidade das soluções aproximadas
que são obtidas utilizando o Método dos Elementos Finitos.
5.1 Condições de Domínio
A condição de equilíbrio no domínio assegura que a variação do campo de tensões equilibra, em
cada ponto, as forças de massa,
 ∂ xσ xx + ∂ yσ xy + f x = 0
em Ω

 ∂ yσ yy + ∂ xσ xy + f y = 0
(13)
enquanto a condição de compatibilidade no domínio define, em cada ponto, as medidas de
deformação em função da variação do campo de deslocamentos:
 ε xx = ∂ x u x

 ε yy = ∂ y u y
γ = ∂ u + ∂ u
y x
x y
 xy
em Ω
(14)
Quando se admite que o material elástico linear é homogéneo e isotrópico, obtém-se a
seguinte definição para as relações constitutivas, isto é, as condições que definem, em cada
ponto, o estado de tensão provocado por um determinado estado de deformação,

E
 σ xx = 1 −ν 2 (ε xx + ν ε yy )


E
(ε yy + ν ε xx ) em Ω
 σ yy =
2
−
1
ν


E
γ xy
 σ xy =
2(1 + ν )

(15)
para estados planos de tensão, sendo E o módulo de elasticidade e ν o coeficiente de Poisson.
A relação constitutiva para estados planos de deformação é a seguinte:

E 1 −ν
 σ xx = 1 − 2ν 1 + ν (ε xx + ν ε yy )


E 1 −ν
(ε yy + ν ε xx ) em Ω
 σ yy =
1
−
2
ν
1
+
ν


E
γ xy
 σ xy =
2(1 + ν )

(16)
As condições de equilíbrio, compatibilidade e de elasticidade (13) a (15) ou (16) estão
expressas matricialmente no Quadro 2, de acordo com as definições (1) e (2) para os vectores de
tensão e deformação e as definições (3) e (4) para os vectores das forças de domínio e dos
deslocamentos, respectivamente.
7
Análise de Estruturas II: Elasticidade Plana e Tridimensional
As expressões que se encontram para os operadores diferenciais de compatibilidade e de
equilíbrio e para a matriz de rigidez são as seguintes:
∂ x

A = 0
∂ y

∂ x
AT = 
0
0 

∂y 
∂ x 
0
∂y
∂y 
∂ x 
(17)
0 
κ + 1 3 − κ
G 
D=
3 −κ κ +1
0 

κ −1
 0
κ − 1
0
em que G = E / 2(1 + ν ) é o módulo de distorção, com κ = (3 −ν ) /(1 +ν ) para estados planos de
tensão e κ = 3 − 4ν para estados planos de deformação, respectivamente.
A relação de elasticidade (9) pode ser generalizada para incluir o efeito de campos residuais:
s = D ( e − e r ) + sr
em Ω
(18)
As tensões residuais, sr , resultam normalmente de erros de fabrico. Um exemplo típico da
utilização do campo de deformações residuais, er , é a modelação de variações térmicas, sendo,
erT = { α ∆T α ∆T
0}
para materiais homogéneos e isótropos, em que α é o coeficiente de dilatação térmica e
∆T ( x, y ) a variação de temperatura.
Exercício 1: Considere a consola triangular representada na Figura 4. Admitindo ser o
seguinte o campo de deslocamentos,
 u x ( x, y ) = 0

 u y ( x , y ) = ( x /L ) d
(19)
com d = −2, 6 /E (m) , verifique que, para um estado plano de tensão, são as seguintes as
definições dos campos de deformação e de tensão (corte puro),
ε xx ( x, y ) = ε yy ( x, y ) = 0; γ xy ( x, y ) = −2, 6 /E
(20)
σ xx ( x, y ) = σ yy ( x, y ) = 0; σ xy ( x, y ) = −1 (kNm −2 )
(21)
calculadas recorrendo às condições de compatibilidade (14) e de elasticidade (15). Confirme
ainda que a condição de equilíbrio no domínio (13) só é verificada para forças de massa nulas:
fx = f y = 0
8
(22)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
y
y
d = 2, 6 /E (m)
uy
L =1m
ux
L
u x ( x, y ) = 0
ν = 0,3
u y ( x , y ) = ( x /L ) d
E = const. (kNm −2 )
x
x
L
a) Geometria e material
b) Deformada
y
y
ε xx = ε yy = 0
γ xy = −2, 6 /E
σ xx = σ yy = 0
σ xy = −1 (kNm −2 )
x
x
c) Estado de deformação
d) Estado de tensão
ty = 0
t x = −1
fy = 0
fx = 0
tx = 0
tx = +
t y = +1
1
2
e) Forças segundo x
ty = −
1
2
f) Forças segundo y
Figura 4: Consola triangular com campo de deslocamentos linear
5.2 Condições de Fronteira
As restantes equações resumidas no Quadro 2 definem as condições de fronteira estáticas (11) e
as condições de fronteira cinemáticas (12). Essas condições também são designadas por
condições de Neumann (ou condições de fronteira naturais) e por condições de Dirichlet (ou
condições de fronteira essenciais), respectivamente.
A fronteira da peça, Γ , é decomposta nas duas regiões em que essas condições são impostas,
a fronteira estática Γ t (ou de Neumann) e a fronteira cinemática Γ u (ou de Dirichlet). Essas
regiões são complementares, Γ = Γ t ∪ Γ u e ∅ = Γ t ∩ Γ u , por não ser fisicamente possível
impor num ponto simultaneamente uma força e o deslocamento correspondente.
9
Análise de Estruturas II: Elasticidade Plana e Tridimensional
A condição de fronteira estática (11) define o estado de tensão na fronteira que equilibra as
forças aplicadas. A forma explícita dessa equação é a seguinte,
 nxσ xx + nyσ xy = tx

 nyσ yy + nxσ xy = ty
em Γ t
(23)
em que nx e n y representam as componentes da normal exterior unitária, como se ilustra na
Figura 5. Quando esta condição é expressa matricialmente, conclui-se que a matriz de equilíbrio
na fronteira é análoga à matriz de equilíbrio no domínio (17), sendo obtida substituindo a
componente da normal unitária exterior o operador diferencial correspondente:
 nx
NT = 
0
0
ny
ny 
nx 
(24)
y
p
y
ny
n
D
E
nx
nx
n
F
σ yy σ
xy
σ xx
B
ny
nx = +
x
(n
2
x
+ n y2 = 1)
ny = −
1
2
C
1
2
A
x
Figura 6: Condições de fronteira
Figura 5: Normal exterior unitária
A fronteira estática da placa representada na Figura 6 é definida pelas linhas de contorno ABC
e DEF, devendo aí ser impostas as seguintes condições:
 (+

 (−
1
2
) σ xx + (−
1
2
) σ xy = tx = 0
1
2
) σ yy + (+
1
2
) σ xy = ty = 0
em Γ AB
 ( 0 ) σ xx + ( − 1) σ xy = tx = 0
em Γ BC

 (− 1) σ yy + ( 0 ) σ xy = ty = 0
 ( 0 ) σ xx + (1) σ xy = tx = 0
em Γ DEF

 (1) σ yy + ( 0) σ xy = ty = − p
A condição de compatibilidade na fronteira, a equação (12), assegura que os deslocamentos
medidos no domínio, junto ao contorno, são coerentes com os deslocamentos que aí estejam
impostos. A forma explícita dessa condição é a seguinte,
10
Análise de Estruturas II: Elasticidade Plana e Tridimensional
 ux = ux

 uy = uy
em Γ u
ou, para o exemplo da Figura 6:
 ux = ux = 0
em Γ AF

 uy = uy = 0
Ilustra-se na mesma figura um terceiro tipo de condição de fronteira, a condição de fronteira
mista ao longo do bordo Γ CD , em que é imposta uma força e a componente complementar do
deslocamento correspondente:
 ux = ux = 0
em Γ CD

(
0
)
σ
+
(1)
σ
=
t
=
0
yy
xy
y

Esta condição de fronteira resulta, normalmente, de simplificações de simetria. A expressão
complementar definiria a condição de fronteira decorrente de uma condição de anti-simetria:
 (1) σ xx + ( 0 ) σ xy = tx = 0

 uy = uy = 0
Exercício 2: Verifique serem as forças de fronteira representadas na Figura 4 que equilibram
o campo de tensões aí definido. Confirme que essas forças estão globalmente em equilíbrio,
isto é, têm resultantes nulas e produzem um momento nulo em torno do eixo ortogonal ao
plano.
Em vez de impor uma força ou o deslocamento correspondente, é possível impor uma relação
entre a força e o deslocamento. Este tipo de condição de fronteira, também designada por
condição de Robin, é utilizado para simular o comportamento de apoios elásticos, como se
ilustra na Figura 7. A condição é escrita na forma,
t = De u em Γ e
(25)
reunindo a matriz De os coeficientes de rigidez que caracterizam a deformabilidade do meio de
apoio.
Γe
Figura 7: Apoio elástico
11
Análise de Estruturas II: Elasticidade Plana e Tridimensional
5.3 Fronteiras Interiores
Interessa referir, ainda, as condições de fronteira que são artificialmente introduzidas quando a
peça é discretizada em elementos finitos, como seria, por exemplo, o segmento BE se a consola
representada na Figura 5 fosse discretizada em dois elementos, como se mostra na Figura 8.
y
y
E
E
t1y , u1y
t y2 , u y2
t1x , u1x
t x2 , u x2
B
B
x
x
Figura 8: Fronteira interior
Figura 9: Elemento de junta
As condições nesta fronteira devem garantir a continuidade dos deslocamentos,
u j = uk
em Γ i
(26)
em que os índices j e k identificam dois elementos que partilham a fronteira interior Γ i , assim
como o equilíbrio das forças em qualquer ponto da fronteira,
t j +tk = t
em Γ i
(27)
sendo t a força aplicada exteriormente sobre a fronteira ( t = 0 no exemplo da Figura 8).
As forças na fronteira de um elemento são calculadas recorrendo à condição de equilíbrio na
fronteira (11), a qual é válida para qualquer secção do domínio da peça,
Nσ j =t j
em Γ i para o elemento j
em que N é a matriz de equilíbrio (24) escrita para a fronteira Γ i do elemento j e t j o vector
das forças que nessa fronteira equilibram o estado de tensão no elemento.
Ou seja, se se seccionar uma peça, na representação de corpo livre daí resultante as forças
(indeterminadas) que se aplicam na secção de corte são calculadas em função do campo de
tensão recorrendo à equação (11). O conceito é idêntico ao utilizado na definição de diagramas
de corpo livre de peças lineares, em que se aplica na secção de corte como força exterior o
esforço aí existente.
Como as normais exteriores de dois elementos que partilham a mesma fronteira interior são
simétricas, a condição de equilíbrio (27) pode ser expressa directamente em termos do estado de
tensão em cada elemento na forma:
12
Análise de Estruturas II: Elasticidade Plana e Tridimensional
N (σ j − σ k ) = t
em Γ i
(28)
É importante notar que, em consequência desta equação, as três componentes do estado de
tensão em cada elemento são relacionadas por apenas duas condições, e não as três que seriam
necessárias para estabelecer o equilíbrio em termos de tensões. Ou seja, permite que o estado de
tensão entre dois elementos seja diferente, σ j ≠ σ k na fronteira que partilham, Γ i , mesmo que
seja nula a força exterior aí aplicada, t = 0 . Portanto, este enfraquecimento da condição de
continuidade do campo de tensão na peça, σ j = σ k se t = 0 , resulta directamente da
discretização da peça em dois elementos distintos.
Exercício 3: Verifique que a condição (28) escrita para a fronteira entre os dois elementos do
exemplo ilustrado na Figura 7 impõe as condições de continuidade σ 1xx = σ xx2 e σ 1xy = σ xy2 mas
permite que σ 1yy ≠ σ yy2 :
σ 1xx − σ xx2 
1 0 0   1
0 
2 
0 0 1  σ yy − σ yy  =  0  em BE

 1
 
2 
σ xy − σ xy 
Exercício 4: Os elementos de junta (unidimensionais, isto é, sem espessura em problemas
planos, como se ilustra na Figura 9) são usados para modelar diferentes condições de contacto
entre elementos. Escreva a condição de fronteira entre dois elementos ligados entre si por um
elemento de junta com as seguintes propriedades: a) Impede o afastamento mas permite o
deslizamento entre elementos, sem atrito; b) Impede o afastamento mas permite o
deslizamento entre elementos, com atrito; c) Permite o movimento elástico entre elementos.
6. Soluções Exactas e Aproximadas
Mantêm-se as classificações anteriormente definidas para os diferentes tipos de solução do
sistema de equações (8) a (12), resumidas no Quadro 2:
• Um campo de tensões, s , que satisfaz as condições de equilíbrio no domínio (8) e na
fronteira (11), incluindo as fronteiras interiores, é, por definição, uma solução
estaticamente admissível;
• Um campo de deslocamentos, u , que é contínuo no domínio da peça e que satisfaz as
condições de fronteira (12), incluindo as fronteiras interiores, é, por definição, uma solução
cinematicamente admissível, sendo o campo de deformações compatível associado, e ,
definido pela condição de compatibilidade no domínio (10);
13
Análise de Estruturas II: Elasticidade Plana e Tridimensional
• A solução exacta é a solução que para além de ser estática e cinematicamente admissível
satisfaz também a relação de elasticidade (9);
• A solução exacta existe e é única, mas pode não ter expressão analítica.
Para o exemplo da consola triangular definido na Figura 4, o campo de deslocamentos (19)
define uma solução cinematicamente admissível, pois é continuo no domínio da peça, satisfaz a
condição de fronteira cinemática ao longo do bordo encastrado,
Γ u ( x = 0) : u x = u y = 0
(29)
e está associado a um campo de deformações (20) compatível.
Para o mesmo problema, o campo de tensões (21) define uma solução estaticamente
admissível se se admitir que as forças de massa são nulas, de acordo com a condição (22), e,
ainda, se as forças exteriores aplicadas equilibrarem esse campo de tensões, ou seja, se as
condições de fronteira estáticas forem as seguintes:
 Γ t ( y = 1) : t x = −1; t y = 0

1
 Γ t ( y = x) : t x = + 2 ; t y = −
(30)
1
2
Nestas condições, a solução é exacta e única, pois os campos de tensão e de deformação
satisfazem também localmente a relação de elasticidade. As reacções no bordo encastrado da
consola são determinadas calculando as forças que aí equilibram o campo de tensão (21):
Γ u ( x = 0) : t x = 0; t y = 1
(31)
p
b
p
b
y
x
y
x
a
a
Figura 10: Placa carregada transversalmente
Figura 11: Placa carregada axialmente
É muito limitado o número de problemas com relevância prática que têm solução analítica,
mesmo quando a geometria da peça e as condições de fronteira são muito simples. Por exemplo,
a consola carregada transversalmente ilustrada na Figura 10 não tem solução analítica exacta, e o
caso mais simples da carga de tracção uniforme só tem solução analítica exacta quando se
desprezam as forças de massa e o efeito de Poisson.
14
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Exercício 5: Considere a placa carregada axialmente representada na Figura 11 e verifique o
seguinte, admitindo um estado plano de tensão: a) A solução u x = ( x /a) d , u y = 0 é uma
solução cinematicamente admissível; b) A solução σ xx = p , σ yy = σ xy = 0 é uma solução
estaticamente admissível quando se desprezam as forças de massa, f x = f y = 0 ; c) Essas
soluções definem a solução exacta, com d = a p /E , quando se despreza o efeito de Poisson.
Para melhor esclarecer as razões que, por regra, impedem a determinação de soluções exactas
para problemas de elasticidade plana (e tridimensional), é conveniente eliminar variáveis e
compactar as equações (8) a (12) que governam o problema, tal como resumidas no Quadro 2.
Tal como se fez para as peças lineares, a condição de compatibilidade no domínio (10) é
usada para eliminar as deformações na condição de elasticidade (9), recorrendo-se à expressão
resultante para o campo de tensões,
s = D A u em Ω
para exprimir as condições de equilíbrio no domínio (8) e na fronteira (11) em função dos
deslocamentos, e juntando a única condição ainda omissa, a condição de fronteira (12):
AT D A u + f = 0 em Ω
N TD Au = t
em Γ t
u = u em Γ u
(32)
(33)
(34)
Qualquer solução do sistema de equações diferenciais (32) satisfaz localmente (ou de maneira
forte) todas as condições de domínio do problema, designadamente as condições de equilíbrio
(8), de elasticidade (9) e de compatibilidade (10).
A técnica geralmente usada para obter essas soluções consiste em combinar as soluções
complementar e particular,
u = uc + u0
em Ω
definindo a primeira o conjunto das soluções da equação homogénea,
AT D A uc = 0 em Ω
e a segunda uma qualquer solução que represente o efeito das forças de massa:
AT D A u0 + f = 0 em Ω
Estas soluções da equação de Navier (32) foram há muito estabelecidas para materiais
homogéneos e isotrópicos, recorrendo a potenciais de deslocamento (funções cujas derivadas
definem o campo de deslocamento, u) ou a potenciais de tensão (funções cujas derivadas
15
Análise de Estruturas II: Elasticidade Plana e Tridimensional
definem o campo de tensão, s). Existem também soluções para materiais homogéneos
anisótropos, sendo mais limitados os casos resolvidos para materiais heterogéneos.
Na maioria das aplicações, a dificuldade de obter soluções exactas para problemas de
elasticidade plana (e tridimensional) não está, portanto, na determinação das soluções da equação
de Navier (32). A dificuldade está em conseguir que essas soluções satisfaçam, também de
maneira forte, as condições de fronteira do problema, definidas pelas equações (33) e (34).
7. Método dos Elementos Finitos
O modelo de deslocamento do Método dos Elementos Finitos é a seguir utilizado para
determinar soluções aproximadas do problema de elasticidade plana definido pelas equações
resumidas no Quadro 2, ou pelo sistema equivalente definido pelas equações (32) a (34). A
aplicação do método é conceptualmente idêntica à adoptada na análise de estruturas reticuladas,
podendo ser resumida em quatro fases:
Primeira fase: Aproximações
• A estrutura é discretizada em elementos finitos;
• O campo de deslocamentos é aproximado em cada elemento usando funções contínuas, na
forma,
u =Ψ d
(35)
sendo Ψ a matriz que reúne as funções de aproximação e d o vector dos deslocamentos
nodais do elemento;
• A condição de compatibilidade (10) é imposta localmente para definir a aproximação do
campo de deformações em cada elemento:
e = Bd
(36)
B = AΨ
(37)
• A relação de elasticidade (9) é imposta localmente para definir o campo de tensões em
cada elemento:
s = DB d
(38)
Segunda fase: Forças Nodais Equivalentes
• A equação resolvente do elemento é estabelecida interpretando-a como uma condição de
equilíbrio de forças nodais equivalentes,
Kd =F
reunindo a matriz de rigidez do elemento as forças devidas aos deslocamentos nodais,
16
(39)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
K = ∫ BT D B d Ω
(40)
F = F f + Ft + Fn
(41)
Ω
e o vector,
as forças nodais equivalentes às forças de massa,
Ff = ∫ Ψ T f d Ω
Ω
(42)
as forças nodais equivalentes às forças aplicadas na fronteira,
Ft = ∫ Ψ T t d Γ
Γ
(43)
e as forças concentradas aplicadas nos nós do elemento, Fn .
Terceira fase: Equação Resolvente
• A solução aproximada em cada elemento está sujeita à condição de ser cinematicamente
admissível, sendo construída de maneira a satisfazer localmente (ou de maneira forte) a
condição de fronteira cinemática (34) da malha de elementos finitos e, ainda, a condição
equivalente (26) entre elementos;
• Essa condição é imposta relacionando os deslocamentos nodais dos elementos, d, com os
deslocamentos nodais da malha de elementos finitos, q, através de uma condição de
incidência nodal:
d =ℑ q
(44)
• As forças nodais equivalentes na malha de elementos finitos definem as resultantes das
contribuições das forças nodais equivalentes geradas em cada elemento,
Q = ℑ TF
(45)
e são utilizadas para estabelecer a equação resolvente do problema:
K* q = Q
(46)
• Este sistema de equações define as condições de equilíbrio das forças nodais equivalentes,
impondo aproximadamente (ou de maneira fraca) as condições de equilíbrio no domínio
(8) e na fronteira estática (11), ou as equações equivalentes (32) e (33), estendidas de modo
a incluírem as condições de equilíbrio (28) nas fronteiras entre elementos.
Quarta fase: Análise da Solução
• Resolvido o sistema (46) nas incógnitas do problema, os deslocamentos nodais da malha
de elementos finitos, q, os deslocamentos, as deformações e as tensões são calculadas em
cada elemento recorrendo às aproximações (35), (36) e (38), depois de determinar os
deslocamentos nodais em cada elemento através da relação de incidência (44).
17
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Este procedimento é a seguir apresentado e interpretado recorrendo a um exemplo simples,
sendo posteriormente sistematizado. Discute-se a definição das funções que são utilizadas para
estabelecer a aproximação em que o método se baseia, a aproximação (35) do campo de
deslocamento em cada elemento. Essa generalização da aproximação é depois utilizada para
ilustrar as operações (44) e (45) de reunião de elementos de que decorre a formulação da
equação resolvente (46) para uma malha de elementos finitos.
Exercício 6: Deduza a equação resolvente elementar (39) e obtenha as definições (40) a (43)
impondo as aproximações (35), (36) (38) na condição de balanço energético (7). Recupere os
mesmos resultados estacionarizando a energia potencial do elemento:
Min Π = 12 ∫ e T s d Ω − ∫ uT f d Ω − ∫ uT t d Γ − uT F
Ω
Ω
Γ
Exercício 7: Generalize a expressão da equação resolvente (39) para incluir a definição do
vector das forças nodais equivalentes a campos de deformação e de tensão residuais (18):
Fr = ∫ B T ( sr − D er ) d Ω
Ω
(47)
Exercício 8: Mostre ser a seguinte a contribuição de uma fronteira elástica (25) para a matriz
de rigidez elementar:
K e = ∫ Ψ T De Ψ d Γ e
Γe
(48)
8. Exemplo de Introdução
O exemplo de aplicação escolhido é o problema de estado plano de tensão representado na
Figura 4, em que se despreza o efeito das forças de massa ( kNm −3 ), como estabelece a condição
(22), e se considera o carregamento indicado na Figura 12a).
De acordo com a identificação das fronteiras definida na Figura 12b), a placa triangular está
encastrada no bordo x = 0 , sujeita a uma carga uniforme transversal no bordo y = 1 , definindo o
lado y = x um bordo livre. A condição de fronteira cinemática (29) mantém-se válida, sendo a
condição de fronteira estática (30) substituída pela seguinte:
 Γ t ( y = 1) : t x = 0; t y = −1

 Γ t ( y = x) : t x = t y = 0
(49)
Este exemplo é resolvido admitindo a mais simples aproximação possível. A placa é
discretizada num único elemento em que se admite ser linear a variação do campo de
deslocamentos, descrita pelos deslocamentos do vértice livre da consola, os deslocamentos
nodais d1 e d 2 identificados na Figura 12c).
18
Análise de Estruturas II: Elasticidade Plana e Tridimensional
p = 1 (kNm −2 )
y
Γ t ( y = 1)
1m
Γ u ( x = 0)
ν = 0,3
E = const.
Γ t ( y = x)
x
1m
a) Carregamento
b) Fronteiras
y
y
F2
d2
1m
σ yy σ
xy
d1
uy
σ xx
1m
ux
x
 u x = ( x) d1

 u y = ( x) d 2
x
1m
F1
 σ xx = (1, 099 E ) d1

 σ yy = (0,330 E ) d1
 σ = (0,385E ) d
2
 xy
1m
c) Aproximação dos deslocamentos
d) Aproximação das tensões
Figura 12: Consola triangular sujeita a uma carga transversal uniforme
Como se usa apenas um elemento, este exemplo não serve para ilustrar as operações de
reunião de elementos para formar a malha de discretização, definidas pelas condições de
incidência nodal (44) e (45), as quais são analisadas posteriormente. O que se pretende ilustrar
são os dois aspectos fundamentais da formulação de deslocamento do Método dos Elementos
Finitos aplicado à solução de problemas de elasticidade plana:
• A solução aproximada é construída de maneira a ser cinematicamente admissível, sendo
escrita em função dos deslocamentos nodais, os deslocamentos d1 e d 2 identificados na
Figura 12c);
• A aproximação resultante para o campo de tensões, definida na Figura 12d), viola, em
geral, as condições de equilíbrio, sendo o equilíbrio imposto sobre forças nodais
equivalentes às forças de massa e de fronteira, as forças F1 e F2 indicadas na mesma
figura.
8.1 Aproximação dos Deslocamentos
A hipótese do campo de deslocamentos variar linearmente no domínio do elemento é formulada
da seguinte maneira ( L = 1 m) ,
19
Análise de Estruturas II: Elasticidade Plana e Tridimensional
u x ( x, y ) = a0 + ( x /L) a1 + ( y /L) a2
u y ( x, y ) = b0 + ( x /L) b1 + ( y /L) b2
sendo importante notar que apenas as componentes de translação do movimento são
aproximadas independentemente. A componente de rotação é uma variável dependente. É
calculada pela equação (5), encontrando-se:
ω z = 12 (b1 − a2 )
Esta aproximação permite representar os três movimentos de corpo rígido no plano,
designadamente duas translações, a0 ≠ 0 com a1 = a2 = 0 e b0 ≠ 0 com b1 = b2 = 0 , e uma
rotação, a2 ≠ b1 ≠ 0 , e, ainda, a mais simples aproximação para o campo de deformações, o
estado de deformação constante, que adiante se define.
Os pesos das funções de aproximação, ai e bi , são escolhidos usando critérios análogos aos
adoptados na formulação dos elementos finitos para peças lineares. São definidos impondo
localmente a condição de fronteira cinemática (29),
a0 = a2 = b0 = b2 = 0
a qual elimina as componentes de corpo rígido, e escolhidos de modo a representar as
componentes do deslocamento num nó do elemento, neste caso o vértice livre da placa,
d1 = u x (1,1) ⇒ a1 = d1
d 2 = u y (1,1) ⇒ b1 = d 2
ver Figura 12c), obtendo-se a seguinte expressão para a aproximação (35) do campo de
deslocamentos:
 u x   x 0   d1 
 =
 
 u y  0 x   d2 
(50)
Sendo o campo de rotação dependente das componentes de translação, as rotações dos nós
não são escolhidas como incógnitas do problema, sendo o vector dos deslocamentos nodais
presente na definição (35) sempre definido em termos das componentes de translação medidas
no referencial global da estrutura.
8.2 Aproximação das Deformações e das Tensões
Em consequência das condições anteriormente impostas sobre a aproximação dos deslocamentos
(50), para assegurar que essa aproximação define uma solução cinematicamente admissível no
sentido forte, isto é, em todos os pontos do domínio da placa e da sua fronteira cinemática, basta
definir a aproximação do campo de deformações impondo localmente a condição de
compatibilidade no domínio (14), encontrando-se o seguinte resultado para a definição (36):
20
Análise de Estruturas II: Elasticidade Plana e Tridimensional
 ε xx  1 0 
  
  d1 
 ε yy  = 0 0   
 γ  0 1   d 2 

 xy  
(51)
Como o campo de deformações é constante, a aproximação (38) que resulta para o campo de
tensões impondo localmente as relações de elasticidade (15) é:
 σ xx  1, 099 E
0 
d 
  
0   1 
 σ yy  = 0,330 E
d
σ   0
0, 385 E   2 
 xy  
(52)
8.3 Condições de Equilíbrio no Domínio e na Fronteira
Como a aproximação linear do campo de deslocamentos está associada a uma aproximação
constante (52) para o campo de tensões e se admite que as forças de massa (22) são nulas,
conclui-se que (contra o que geralmente sucede) a condição de equilíbrio (13) é localmente
satisfeita neste exemplo de aplicação.
(0,385 E ) d 2
(1, 099 E ) d1
(0,330 E ) d1
(0,385 E ) d 2
fx = 0
fy = 0
+ (0, 777 E ) d1
− (0, 233E ) d1
− (0, 272 E ) d 2
+ (0, 272 E ) d 2
a) Forças segundo x
b) Forças segundo y
Figura 13: Forças de massa e de fronteira equilibradas pela aproximação do campo de tensões
No entanto, quando se recorre à definição (23) para calcular as forças na fronteira que
equilibram o estado de tensão,
 σ xx 
 tx  0 0 1   
 (0,385 E ) d 2 
Γ ( y = 1) :   = 
σ yy  = 


 (0,330 E ) d1 
 t y  0 1 0 σ 
 xy  y = 1
+1
 tx   2
Γ ( y = x) :   = 
 t y   0
0
−1
2
σ 
  xx 
 + (0, 777 E ) d1 − (0, 272 E ) d 2 
=
 σ

+1  yy 
 − (0, 233E ) d1 + (0, 272 E ) d 2 
 σ 
2
 xy  y = x
−1
2
21
Análise de Estruturas II: Elasticidade Plana e Tridimensional
 t x   −1
Γ ( x = 0) :   = 
ty   0
 σ xx 
0 
 −(1, 099 E ) d1 
 σ yy  = 


−(0, 385 E ) d 2 
−1  

 σ xy  x = 0
0
0
conclui-se que não é possível escolher valores para os graus de liberdade do problema, os
deslocamentos nodais d1 e d 2 , que permitam impor localmente as condições de fronteira
estáticas (49), como se ilustra na Figura 13.
Para obter uma solução aproximada útil torna-se necessário impor as condições de equilíbrio
de uma maneira fraca, recorrendo-se novamente ao critério de determinar os deslocamentos
nodais equacionando o trabalho das forças interiores ao das forças exteriores.
8.4 Equação Resolvente
A equação (39) que se obtém aplicando esse critério (ver Exercício 6) tem a seguinte expressão:
0
 0,5(1, 099 E )
  d1   0 
 =


0
0,5(0,385E )   d 2   −0,5

(53)
A matriz de rigidez é calculada aplicando a definição (40), explorando o facto de serem
constantes os campos de tensão e de deformação no domínio da consola triangular (com área
Ω = 0,5 m2 ):
K = ∫ BT D B d Ω = BT D B ∫
Ω
1
0
K
K =  11
 K 21
∫
1
x
1 dy dx = 0,5 B T D B
K12   0,5(1, 099 E )
0

=

K 22  
0
0,5(0,385E ) 
(54)
Como as forças de massa são nulas, f = 0 em Ω , e não existem forças aplicadas no nó livre
da consola, só a força transversal (49) contribui para o vector das forças nodais equivalentes (41)
obtendo-se o seguinte resultado aplicando as definições (42) e (43):
F   0 
F =  1=

 F1   −0,5
 x 0  f x = 0 
0
 0 x   f = 0  dy dx =  0 

  y
 

T
Ff = ∫
1
0
∫
1
x
 tx = 0 
 x 0

 dx +
0 x 

 y = 1 t y = −1
T
Ft = ∫
1
0
 tx = 0 
 x 0
 0 

 dx = 

0 x

 y= x ty = 0 
 −0,5
T
∫
1
0
22
(55)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
8.5 Interpretação da Equação Resolvente
Na interpretação dada ao sistema resolvente (53) no contexto da aplicação do Método dos
Deslocamentos na análise de estruturas reticuladas, cada equação define uma condição de
equilíbrio entre dois conjuntos de forças nodais, as forças nodais devidas aos deslocamentos
nodais qi e as forças nodais aplicadas, Fi .
d1 = 1
d2 = 1
p =1
1m
1m
K 22
K 21
K11
a) Acção de d1 = 1
F2
F1
K12
b) Acção de d 2 = 1
c) Acção do carregamento
Figura 14: Interpretação dos termos da equação resolvente
Como se ilustra na Figura 14, continua a ser possível interpretar o coeficiente K ij da matriz
de rigidez K como a força nodal Fi devida ao deslocamento nodal q j = 1 e, no termo
independente do sistema (53), os coeficientes do vector de forças nodais F como sendo as
forças nodais Fi aplicadas. A diferença essencial é que essas forças nodais representam agora
forças concentradas equivalentes às que equilibram o campo de tensões no domínio e na
fronteira do domínio bidimensional agora em análise.
Nas Figura 15a) e 15c) definem-se os sistemas de forças que equilibram a aproximação das
tensões devidos aos deslocamentos unitários, de acordo com os resultados apresentados na
Figura 13, e nas Figuras 15b) e 15d) definem-se as forças nodais equivalentes.
Sendo nulas as forças de massa e linear a aproximação do campo de deslocamentos, essas
forças são calculadas, como adiante se mostra, determinando a resultante das forças de fronteira
e atribuindo metade dessa resultante a cada nó de extremidade.
23
Análise de Estruturas II: Elasticidade Plana e Tridimensional
t y = +0,330 E
tx = 0
t x = −1, 099 E
fx = 0
ty = 0
fy = 0
t x = +0, 777 E
t y = −0, 233E
a) Forças de domínio e de fronteira devidas a d1 = 1
0
1
2
0
2
2
(−1, 099 E )
1
2
0
(+0,330 E )
(+0, 777 E )
= 12 (+1, 099 E )
2
2
(−0, 233E )
= 12 (−0,330 E )
0
b) Forças nodais equivalentes devidas a d1 = 1
t x = +0,385 E
tx = 0
ty = 0
t y = −0, 385 E
fx = 0
fy = 0
t x = −0, 272 E
t y = +0, 272 E
c) Forças de domínio e de fronteira devidas a d 2 = 1
0
0
1
2
(+0, 385 E )
0
2
2
(−0, 272 E )
1
2
(−0, 385 E )
= 12 (−0,385E )
2
2
(+0, 272 E )
= 12 (+0,385E )
0
d) Forças nodais equivalentes devidas a d 2 = 1
Figura 15: Forças nodais equivalentes devidas à aproximação do deslocamento
24
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Os resultados das Figuras 15b) e 15d) recuperam a definição (54) da matriz de rigidez,
mostrando que:
• As forças nodais equivalentes
K11 = 0 +
• As
2
2
F1
e
F2
devidas ao deslocamento
(0, 777 E ) = 0,5(1, 099 E ) e K 21 = 12 (+0,330 E ) +
mesmas
forças
K12 = 12 (−0,330 E ) +
2
2
devidas
ao
deslocamento
(+0, 233E ) = 0 e K 22 = 0 +
2
2
2
2
d1 = 1 são
(−0, 233E ) = 0 ;
d2 = 1
são,
respectivamente,
(0, 272 E ) = 0,5(0,385 E ) .
Quando se aplica o mesmo critério para determinar as forças nodais equivalentes ao
carregamento da consola obtém-se a definição (55), como se ilustra na Figura 16.
p = 1 kNm −2
0,5 kNm −1
1m
a) Carregamento
b) Forças equivalentes
Figura 16: Forças nodais equivalentes ao carregamento
8.6 Análise da Solução
Depois de calcular a solução do sistema (53), d1 = 0 e d 2 = −2, 6 / E (m) , aplicam-se as
definições (50) a (52) para determinar as aproximações dos deslocamentos, deformações e
tensões. A solução que assim se obtém está representada na Figura 4, concluindo-se que:
• A solução é cinematicamente admissível e produz uma aproximação coerente para a
deformada, ilustrada na Figura 4b);
• Como a aproximação dos deslocamentos é linear e o material homogéneo e isótropo,
obtém-se uma aproximação constante para o campo de tensões, definida na Figura 4d);
• Essa aproximação verifica (neste caso particular) a condição de equilíbrio no domínio (por
serem nulas as forças de massa), mas viola as condições de equilíbrio na fronteira;
• O carregamento dado, representado na Figura 12a) e definido pelas condições de fronteira
(49), não é recuperado pelo sistema de forças que equilibra na fronteira estática a
aproximação do campo de tensão, definido nas Figuras 4e) e 4f) e que corresponde ao
carregamento definido na Figura 17;
25
Análise de Estruturas II: Elasticidade Plana e Tridimensional
• No entanto, esses dois sistemas de forças têm as mesmas forças nodais equivalentes, como
se ilustra na Figura 18, por ser apenas isso o que se impõe ao estabelecer a equação
resolvente (39) do Método dos Elementos Finitos.
1 kNm −2
F2 = −0,5 kNm −1
F1 = 0
1m
1 kNm −2
1m
Figura 17: Forças na fronteira em
equilíbrio com a aproximação das tensões
Figura 18: Forças nodais equivalentes às
forças dadas e às forças calculadas
8.7 Refinamento e Convergência
Tal como se fez na análise de estruturas reticuladas, as soluções obtidas para problemas de
elasticidade plana podem ser melhoradas mantendo o grau de aproximação e aumentando o
número de elementos de discretização da peça (refinamento-h), ou mantendo a malha de
discretização e aumentando o grau da aproximação (refinamento-p).
Na Figura 19 apresentam-se as soluções obtidas para o problema da consola quando se
subdivide a malha e se mantém o grau de aproximação (linear) em cada elemento. A solução
mais refinada aí apresentada, em que se nota a localização da concentração de tensões nos cantos
da secção de encastramento, está já muito próxima da solução exacta.
A análise desses resultados permite estabelecer conclusões análogas às obtidas na análise de
peças lineares:
• A convergência em deslocamentos é relativamente rápida, sendo muito mais lenta a
convergência em tensões (a convergência para a função que se aproxima directamente é
mais rápida do que a convergência para a sua derivada);
• A solução é localmente compatível, no domínio e na fronteira, mas mais rígida do que a
solução exacta (subestima o deslocamento máximo);
• A solução é localmente desequilibrada, no domínio e na fronteira, e não está do lado da
segurança (subestima a tensão máxima);
• A convergência para a solução exacta é ainda fraca sempre que se reconhece a malha de
elementos finitos na representação dos campos de tensão (desequilíbrio entre elementos).
26
Análise de Estruturas II: Elasticidade Plana e Tridimensional
1 elemento
4 elementos
384 elementos
15000 elementos
Figura 19: Refinamento-h da solução da consola triangular (elementos lineares)
A segunda opção de refinamento (refinamento-p) está ilustrada nas Figuras 20 e 21 para o
exemplo da consola quadrada (a = b) representada na Figura 10. O problema é resolvido com
elementos de 3 nós (aproximação linear dos deslocamentos) e 6 nós (aproximação quadrática),
os quais são adiante definidos. As duas malhas têm o mesmo número de nós livres, pelo que os
sistemas resolventes (46) correspondentes envolvem o mesmo número de incógnitas (dois
deslocamentos por nó livre).
27
Análise de Estruturas II: Elasticidade Plana e Tridimensional
512 elementos lineares
128 elementos quadráticos
Figura 20: Solução da consola quadrada com elementos lineares e quadráticos (289 nós)
512 elementos lineares 128 elementos quadráticos
Figura 21: Solução da consola quadrada com elementos lineares e quadráticos (289 nós)
28
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Ambas as soluções são cinematicamente admissíveis mas qualquer delas ainda está longe de
aproximar correctamente o campo de tensão, pois é ainda visível o desequilíbrio entre elementos.
No entanto estes resultados servem para ilustrar outra conclusão tirada na análise de estruturas
reticuladas pelo Método dos Elementos Finitos:
• Para o mesmo número de graus de liberdade, a qualidade da solução cresce com o grau da
aproximação do campo de deslocamentos.
9. Discretização e Aproximação
Na aplicação do Método dos Elementos Finitos à solução de problemas de Elasticidade Plana o
domínio é decomposto em elementos com geometria simples de modo a viabilizar e facilitar as
várias fases de aplicação do método resumidas na Secção 7.
A utilização de elementos simples, tipicamente elementos com três e quatro lados, assegura a
primeira condição de facilitar a representação, com o rigor desejado, da geometria e das
condições de fronteira do domínio em análise. Na Figura 22 ilustra-se a discretização de um
açude usando elementos triangulares de 3 nós. A modelação da galeria no centro do açude pode
ser melhorada diminuindo a dimensão dos elementos e/ou aumentando o número de nós do
elemento, como adiante se mostra.
0,4
2m
0,5
1
0,3 0,2
1
1
db
y
da
1
dc
dd
x
2
1
1
1
1
2
Figura 22: Discretização de um açude com elementos triangulares de 3 nós
Uma segunda condição importante é ser fácil definir expressões gerais para as funções usadas
na aproximação (35) do campo de deslocamentos. A terceira condição, essencial à formulação
em termos de deslocamentos do Método dos Elementos Finitos, que aqui se adopta, é assegurar
que essas funções produzam soluções cinematicamente admissíveis.
A última condição, muito importante em termos de implementação numérica, é a de facilitar o
cálculo dos integrais que definem a matriz de rigidez (40) de cada elemento e os vectores das
forças nodais equivalentes às forças de massa (41) e de fronteira (43).
29
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Como adiante se mostra, a maneira mais eficaz de satisfazer esses objectivos é recorrer ao
conceito de elemento isoparamétrico. No entanto, nesta fase da apresentação é suficiente analisar
como se pode aproximar uma função sobre os dois tipos de elementos acima referidos, usando a
mais simples aproximação que cada um deles permite, escrita na forma,
N
f ( x, y ) = ∑ Ψ i ( x, y ) f i
(56)
i =1
designadamente o elemento triangular de 3 nós ( N = 3) e o elemento rectangular de 4 nós
( N = 4) representados nas Figura 23 e 24.
( x4 , y4 )
( x3 , y3 )
( x3 , y3 )
b
( x2 , y2 )
y
y
( x1 , y1 )
( x1 , y1 )
( x2 , y2 )
a
x
x
Figura 23: Elemento triangular de 3 nós
Figura 24: Elemento rectangular de 4 nós
Mantém-se o princípio de basear a aproximação em funções polinomiais, definindo-as de
modo a terem valor unitário num nó e nulo nos restantes,
 1 se j = i
 0 se j ≠ i
Ψ i (x j , y j ) = 
(57)
para assegurar que os coeficientes da aproximação, f i , representam o valor da função nos nós do
elemento. Para além disso, é necessário assegurar que a aproximação (56) permite representar a
função polinomial mais simples, a função unitária:
N
∑Ψ
i =1
i
( x, y ) = 1
(58)
9.1 Aproximação Linear
Em consequência das condições acima impostas, as funções presentes na aproximação (56) para
o elemento de 3 nós definem os planos representados na Tabela 1, com a seguinte expressão
geral,
Ψ i ( x, y ) =
1
(α i + β i x + γ i y ) com i = 1, 2, 3
2A
em que A representa a área do elemento triangular, dada por,
30
Análise de Estruturas II: Elasticidade Plana e Tridimensional
2 A = α1 + α 2 + α 3
se a numeração dos nós for sequencial e no sentido inverso ao dos ponteiros do relógio, tendo os
termos constantes as seguintes expressões,
α i = x j yk − xk y j
β i = y j − yk
γ i = xk − x j
em que i ≠ j ≠ k e onde se permutam os índices pela sequência natural:
α1 = x2 y3 − x3 y2 ; α 2 = x3 y1 − x1 y3 ; α 3 = x1 y2 − x2 y1
( x3 , y3 )
( x3 , y3 )
1
1
( x2 , y2 )
( x3 , y3 )
( x2 , y2 )
( x2 , y2 )
1
( x1 , y1 )
Ψ 1 = (α1 + β1 x + γ 1 y ) /2 A
∂ xΨ 1 = β1 /2 A
∂ yΨ 1 = γ 1 /2 A
( x1 , y1 )
( x1 , y1 )
Ψ 2 = (α 2 + β 2 x + γ 2 y ) /2 A
∂ xΨ 2 = β 2 /2 A
∂ yΨ 2 = γ 2 /2 A
Ψ 3 = (α 3 + β3 x + γ 3 y ) /2 A
∂ xΨ 3 = β 3 /2 A
∂ yΨ 3 = γ 3 /2 A
Tabela 1: Elemento triangular de 3 nós
Estes resultados mostram que a aproximação (56) para N = 3 é linear e completa, isto é,
envolve todos os termos lineares, x e y , e todos os monómios de grau inferior, que agora se
reduz ao termo constante.
Exercício 9: Recupere a aproximação (50) do campo de deslocamentos na consola triangular
representada na Figura 12 usando as funções de aproximação definidas na Tabela 1.
9.2 Aproximação Bilinear
Quando o mesmo processo de construção das funções de aproximação é aplicado ao domínio
rectangular representado na Figura 24, trabalhando apenas com os nós colocados nos vértices,
obtêm-se as funções definidas e representadas na Tabela 2, em que se usa a notação x ' = x − x1
y ' = y − y1 , para simplificar a definição das funções de aproximação.
31
Análise de Estruturas II: Elasticidade Plana e Tridimensional
A análise dessas funções mostra que a aproximação (56) para N = 4 é quadrática mas
incompleta, isto é, envolve apenas o termo bilinear, x y (ou x ' y ' na notação usada), dos três
monómios quadráticos possíveis, designadamente x 2 , x y e y 2 .
( x4 , y4 )
( x4 , y4 )
1
( x3 , y3 )
( x3 , y3 )
( x1 , y1 )
( x1 , y1 )
1
( x2 , y2 )
( x2 , y2 )
Ψ 1 = (1 − x ' /a) (1 − y ' /b)
∂ xΨ 1 = −(1 − y ' /b) /a
∂ yΨ 1 = −(1 − x ' /a ) /b
Ψ 2 = (1 − y ' /b) x ' /a
∂ xΨ 2 = (1 − y ' /b) /a
∂ yΨ 2 = − x ' /ab
1
( x4 , y4 )
( x4 , y4 )
1
( x1 , y1 )
( x3 , y3 )
( x1 , y1 )
( x3 , y3 )
( x2 , y2 )
( x2 , y2 )
Ψ 3 = x ' y ' /ab
∂ xΨ 3 = y ' /ab
∂ yΨ 3 = x ' /ab
Ψ 4 = (1 − x ' /a) y ' /b
∂ xΨ 4 = − y ' /ab
∂ yΨ 4 = (1 − x ' /a ) /b
Tabela 2: Elemento rectangular de 4 nós ( x ' = x − x1 ; y ' = y − y1 )
9.3 Grau da Aproximação no Domínio e na Fronteira
A aproximação (56) é adiante generalizada para obter uma maior precisão na representação da
função, tanto para elementos triangulares como para elementos quadrangulares.
Esse enriquecimento é obtido aumentando o número de termos da aproximação, N , ou seja, o
número de nós do elemento de acordo com a condição (57), garantindo que se incluem na
aproximação tantos termos quantos possíveis de grau inferior ao termo de maior grau, M , na
aproximação (56).
32
Análise de Estruturas II: Elasticidade Plana e Tridimensional
O problema que se põe ao escolher um elemento com N nós para realizar uma dada análise é
saber qual é o grau, M , que se está a usar na aproximação no domínio do elemento, e o grau da
aproximação na fronteira, M f .
A maneira mais expedita para obter esta informação é recorrer ao Triângulo de Pascal
representado na Figura 25, o qual é construído de maneira a agrupar em cada linha todos os
monómios possíveis de um dado grau. Os lados do triângulo com origem no termo constante
definem o grau da aproximação (56) nos lados do elemento. Os termos interiores identificam o
grau dos monómios da aproximação (56) presentes no domínio do elemento.
Constante
1
x
x2
x
x4
Linear
y
y2
xy
3
2
x y
xy
x3 y
Quadrático
2
x2 y2
y
3
xy 3
Cúbico
y4
Quártico
Figura 25: Triângulo de Pascal
Se se admitir que a aproximação na fronteira do elemento é completa, o que se verifica tanto
para elementos triangulares como quadrangulares, conclui-se que o grau de aproximação num
lado com N f nós é M f = N f − 1 . É o que se verifica para o elemento triangular de 3 nós e para
o elemento rectangular de 4 nós anteriormente definidos: a aproximação é linear nos lados de
ambos os elementos ( N f = 2 , M f = 1 ), como se ilustra nas Tabelas 1 e 2.
Nas Figuras 26 e 27 definem-se outros tipos de elementos triangulares (de 6 e 10 nós) e
quadrangulares (de 8 e 9 nós). A todos eles se aplica a definição anteriormente dada para o grau
da aproximação (56) nos lados dos elementos: quadrática nos lados com 3 nós e cúbica nos lados
com 4 nós.
η
η
η
3
5
7
6
8
1
1
4
6
1
9
2
1
1
2
ξ
1
10
5
3
2
3
1
ξ
1
Figura 26: Elementos triangulares com 3, 6 e 10 nós.
33
1
4
ξ
Análise de Estruturas II: Elasticidade Plana e Tridimensional
η
η
4
3
η
5
7
5
7
6
6
1
1
1
4
8
ξ
ξ
1
1
4
8
2
1
1
1
2
ξ
9
1
2
1
1
1
3
1
1
1
3
Figura 27: Elementos quadrangulares com 4, 8 e 9 nós.
Na literatura sobre o Método dos Elementos Finitos designam-se por serendipianos os
elementos sem nós interiores e Lagrangianos os elementos que os têm. Essa distinção decorre da
escolha das funções de aproximação, sabendo-se que, para a mesma ordem de aproximação, os
elementos Lagrangianos têm melhor comportamento.
Se se admitir que a aproximação (56) num elemento triangular com N nós é completa, para
determinar o grau no domínio do elemento, M , basta varrer o Triângulo de Pascal por linhas e
contabilizar tantos monómios quanto o número de nós do elemento.
Aplicando este processo, conclui-se que a aproximação no elemento de 3 nós é linear, M = 1 ,
como anteriormente se verificou, sendo quadrática, M = 2 , e cúbica, M = 3 para os elementos
triangulares com 6 e 10 nós representados na Figura 25.
O processo para determinar o grau da aproximação (56) num elemento quadrangular com N
nós é semelhante mas dificultado pelo facto da aproximação ser incompleta, isto é, não envolver
todos os monómios de grau M , ou mesmo M − 1 , sendo M o maior grau envolvido na
aproximação.
Já se verificou que o rectângulo de 4 nós é completo nos termos lineares mas só contém o
termo bilinear dos monómios quadráticos do Triângulo de Pascal. O elemento de 8 nós
representado na Figura 26 contém todos os termos quadráticos, mas apenas dois dos monómios
cúbicos, os termos x 2 y e x y 2 . Para manter a simetria da aproximação, isto é, para não dar maior
peso aos monómios em x ou em y , o nó adicional no elemento de 9 nós é usado para introduzir
o termo x 2 y 2 , sendo portanto a aproximação incompleta nos termos cúbicos e quárticos.
Estes elementos e estes critérios de definição das funções de aproximação serão adiante
utilizados para definir os elementos isoparamétricos usados na solução de problemas de
Elasticidade Plana.
34
Análise de Estruturas II: Elasticidade Plana e Tridimensional
10. Generalização da Aproximação
As funções de aproximação anteriormente definidas podem ser utilizadas para interpolar uma
qualquer função definida num domínio plano. Por exemplo, para representar a topografia de uma
região, pode-se triangularizar o terreno, definir as cotas nos nós da malha de discretização e
aproximar o relevo usando a aproximação (56) em cada um dos elementos, com N = 3 ,
representando f i a cota do ponto do terreno que coincide com esse nó.
A mesma ideia é aplicada à aproximação do campo de deslocamentos num elemento finito
plano, em que os coeficientes f i da aproximação (56) passam a representar as componentes do
deslocamento nos nós de cada elemento em que a estrutura foi discretizada. Tomando como base
essa aproximação do campo de deslocamentos, pode-se determinar as aproximações
correspondentes para os campos de deformação e de tensão. É esta primeira fase da descrição
sumária do Método dos Elementos Finitos apresentada na Secção 7 que a seguir se analisa:
• A discretização da estrutura em elementos finitos;
• A aproximação do campo de deslocamentos em cada elemento na forma (35);
• A determinação dos campos de deformação (36) e de tensão (38) correspondentes;
• A verificação das condições de continuidade desses campos quando os elementos são
reunidos para constituir a estrutura.
10
20 kPa
fx = 0
y
2m
f y = −20 kNm −3
E = 200 GPa
ν = 0,3
x
1
1
Figura 28: Dados e discretização para o exemplo da placa trapezoidal
10.1 Aproximação do Campo de Deslocamento
Independentemente da geometria do elemento, as componentes (de translação) do campo de
deslocamento são sempre medidas no referencial global da malha em que o elemento se insere.
Para além disso, a aproximação (56) é aplicada independentemente a cada componente do
deslocamento, sendo também os deslocamentos nodais medidos no referencial global, de acordo
com a sequência de numeração dos nós, como se mostra na Figura 29:
35
Análise de Estruturas II: Elasticidade Plana e Tridimensional
N
u x ( x, y ) = ∑ Ψ i ( x, y ) dix
i =1
(59)
N
u y ( x, y ) = ∑ Ψ i ( x, y ) diy
i =1
De acordo com esta aproximação, quando se provoca um deslocamento no nó j segundo a
direcção x, d jx , e se impedem todos os outros deslocamentos nodais, d jy = 0 e d ix = d iy = 0 para
i ≠ j , o elemento deforma-se apenas com deslocamentos segundo x,
u x ( x, y ) = Ψ j ( x, y ) d jx ; u y ( x, y ) = 0
(60)
obtendo-se um resultado análogo, mas segundo y, quando se impõe um deslocamento nodal
nessa direcção:
u x ( x, y ) = 0; u y ( x, y ) = Ψ j ( x, y ) d jy
d4 y
d3 y
d3 x
d2 y
3
uy
2
ux
y
1
d4x 4
d2 x
d3 y
3 d3 x
uy
ux
y
d1x
d1x
1
d1y
d1 y
2 d2 x
d2 y
x
b) Elemento rectangular de 4 nós
x
a) Elemento triangular de 3 nós
Figura 29: Convenção para a medição das componentes do campo de deslocamento
A expressão matricial da aproximação (59) é escrita na forma que for mais adequada para a
questão que se estiver a tratar. Pode ser conveniente definir separadamente cada componente,
uα = Ψ dα
(61)
com α = x ou α = y , reunindo o vector-linha Ψ as funções de aproximação,
Ψ = {Ψ 1 Ψ 2
⋯ Ψ N}
e o vector-coluna dα as componentes do deslocamentos nodais:
 d1α 
d 


dα =  2α 
 ⋮ 
 d Nα 
36
(62)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Alternativamente, pode ser conveniente escrever matricialmente a definição (61)
simultaneamente para ambas as componentes,
 u x  Ψ 0   d x 
 =
 
uy   0 Ψ   d y 
(63)
em que 0 é o vector-linha com N coeficientes nulos, ou recorrer à forma mais compacta (35) da
aproximação (59), em que:
 ux 
u= 
uy 
Ψ
Ψ =
0

0 Ψ 
 dx 
d = 
dy 
d3 y
d 4 y d3 y
3 d 3x
d1x
d4 x 4
F3 y
3 d 3x
3 F3x
F4 x 4
2
1
2 d 2 x d1x 1
2 d2 x
d1y d 2 y
d1y d 2 y
1
F4 y F3 y
F1x
3 F3x
1
2 F2 x F1x 1
2 F2 x
F1y F2 y
F1y F2 y
1
Figura 30: Deslocamentos e forças nodais na placa trapezoidal
Identificam-se na Figura 30 os deslocamentos nodais da placa trapezoidal (assim como as
forças correspondentes, para uso posterior). Como adiante se irá verificar, esta discretização é
inaceitável em termos práticos, pois produz uma aproximação muito fraca da solução para o
carregamento e para as condições de apoio definidas na Figura 28. Para além disso, não é boa
prática usar elementos com graus de aproximação diferentes na análise de uma estrutura.
As expressões que se obtêm para o vector (62) que reúne as funções de aproximação das
componentes do deslocamento são as seguintes para cada elemento, de acordo com as definições
dadas nas Tabelas 1 e 2:
Ψ
(1)
=
{Ψ
Ψ 2(1) Ψ 3(1) }
(1)
1
{1− x
37
x − 12 y
1
2
y}
(64)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Ψ
(2)
=
{Ψ
(2)
1
Ψ 2(2) Ψ 3(2) Ψ 4(2) }
{ 12 (2 − x)(2 − y)
− 12 (1 − x)(2 − y ) − 12 (1 − x) y
1
2
(2 − x) y }
(65)
10.2 Continuidade do Campo de Deslocamento
A condição de continuidade dos deslocamentos no domínio dos elementos é implicitamente
assegurada pelas funções de aproximação. Para além disso, e de acordo com a análise feita na
Secção 9, essas funções variam linearmente nas fronteiras dos elementos do exemplo em análise,
pois ambos os elementos considerados têm 2 nós por lado, como se ilustra na Figura 31 para o
deslocamento d 3(1)x = d 4(2)
x =d.
d
3
d
4
1
2
d
3
1
2
a) Deformadas dos elementos
b) Deformada da estrutura
Figura 31: Deformadas devidas ao deslocamento d 3(1)x = d 4(2)
x =d
Por exemplo, no lado definido pelos nós 2 e 3 do elemento 1, o segmento definido por x = 1 e
0 ≤ y ≤ 2 (ver Figura 28) tem-se, usando a expressão (60) com d 3x(1) = d , e a definição (64):
 u x(1) ( x = 1, y ) =Ψ 3(1) ( x = 1, y ) d = ( 12 y ) d
Γ ( x = 1)  (1)
 u y ( x = 1, y ) = 0
Se se repetir o processo para o lado definido pelos nós 1 e 4 do elemento 2, usando agora a
expressão (60) com d 4(2)
x = d e a definição (65) para as funções do elemento, obtém-se o mesmo
resultado final:
 u x(2) ( x = 1, y ) = Ψ 4(1) ( x = 1, y ) d = ( 12 y ) d
(2)
 u y ( x = 1, y ) = 0
Γ ( x = 1) 
Consequentemente, os dois elementos têm deslocamentos compatíveis ao longo do lado que
partilham, mostrando-se na Figura 31b) a deformada cinematicamente admissível que se obtém
para a placa trapezoidal quando se reúnem os elementos.
É importante notar que se simplifica nessa figura a representação das condições de apoio
recorrendo a apoios rígidos pontuais. Como, para a aproximação feita, os deslocamentos variam
38
Análise de Estruturas II: Elasticidade Plana e Tridimensional
linearmente ao longo dos lados, as condições de encastramento deslizante são exactamente
reproduzidas colocando apoios móveis nos nós afectados por essa condição de apoio. O nó fixo
modela a combinação do efeito das duas condições de encastramento deslizante.
10.3 Aproximação do Campo de Deformação
Para garantir que a aproximação é cinematicamente admissível no sentido forte, a deformação
causada pela aproximação (59) é determinada impondo a condição de compatibilidade no
domínio (14), ficando:
N
ε xx = ∑
i =1
N
ε yy = ∑
i =1
N
γ xy = ∑
i =1
∂Ψ i
d ix
∂x
∂Ψ i
d iy
∂y
(66)
N
∂Ψ i
∂Ψ i
d ix + ∑
d iy
∂y
i =1 ∂ x
De acordo com esta aproximação, quando se provoca um deslocamento no nó j do elemento
segundo a direcção x, d jx , e se impedem todos os outros deslocamentos nodais, d jy = 0 e
d ix = d iy = 0 para i ≠ j , o elemento não tem deformação axial segundo y,
ε xx =
∂Ψ j
∂x
d jx ; ε yy = 0; γ xy =
∂Ψ j
∂y
d jx
obtendo-se um resultado análogo, mas segundo y, quando se impõe um deslocamento nodal
nessa direcção:
ε xx = 0; ε yy =
∂Ψ j
∂y
d jy ; γ xy =
∂Ψ j
∂x
d jy
Na notação matricial (36), é a seguinte a forma explícita da matriz (37) que define as
deformações compatíveis com a aproximação (59) dos deslocamentos:
 ∂ xΨ 1

B= 0
 ∂ yΨ 1

∂ xΨ 2
⋯
∂ xΨ N
0
0
⋯
0
⋯
⋯
0
∂ yΨ 1
∂ xΨ 1
∂ yΨ 2
∂ xΨ 2
⋯
⋯
∂ yΨ 2
∂ yΨ N
0 

∂ yΨ N 
∂ xΨ N 
(67)
A partição feita nesta definição distingue as deformações devidas aos deslocamentos nodais
segundo x e segundo y, d x e d y , respectivamente, por ser por vezes conveniente escrever a
equação (36) na forma,
e =  Bx
 dx 
B y    = Bx d x + B y d y
dy 
39
(68)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
em que, de acordo com a definições (2) e (67):
 ∂ xΨ 1

Bx =  0
 ∂ yΨ 1

 0

B y =  ∂ yΨ 1
 ∂ xΨ 1

∂ xΨ 2
⋯
0
∂ yΨ 2
⋯
⋯
0
⋯
∂ yΨ 2
∂ xΨ 2
⋯
⋯
∂ xΨ N 

0 
∂ yΨ N 
0 

∂ yΨ N 
∂ xΨ N 
As definições que se obtêm para os elementos da placa trapezoidal são as seguintes,
 −2
1
B =  0
2
 0
2
(1)
B
(2)
 −2 + y
1
= 
0
2
 −2 + x
0
−1
2− y
y
0
1− x
0
−1 + x
0
0
0
0 0
1 −2
−1
2
−y
0
1
0 
(69)
0
0
0
0 −2 + x
2 − x −2 + y
1− x
2− y
−1 + x
y
0
2 − x 
− y 
(70)
mostrando que a aproximação do campo de deformação é constante em elementos triangulares
de 3 nós e linear em elementos rectangulares de 4 nós.
10.4 Continuidade do Campo de Deformação
Estes resultados permitem analisar o campo de deformações ao longo do lado partilhado pelos
dois elementos de discretização da placa trapezoidal quando se impõe a deformada representada
na Figura 31a).
O campo de deformações no elemento 1 é determinado multiplicando a terceira coluna da
matriz de compatibilidade (69) por d 3x(1) = d ,
ε xx(1) = 0; ε yy(1) = 0; γ xy(1) = ( 12 ) d
e o campo de deformações no elemento 2 obtém-se multiplicando a quarta coluna da matriz de
compatibilidade (70) por d 4(2)
x = d , para x = 1 :
ε xx(2) = (− 12 y ) d ; ε yy(2) = 0; γ xy(2) = ( 12 ) d
Conclui-se, portanto, que a deformação axial ε yy e a distorção γ xy são contínuas entre
elementos (o que geralmente não sucede nas soluções obtidas com elementos finitos) mas que a
deformação axial ε xx não o é. No entanto, a deformada definida na Figura 31 é compatível no
domínio e na fronteira da placa, pois a definição de admissibilidade cinemática não exige a
continuidade do campo de deformações.
40
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Tal como para as peças lineares, e pelas mesmas razões, as deformações em estados planos de
tensão ou de deformação podem ser descontínuas, o que sucederá se houver descontinuidades
nas propriedades do material estrutural ou nas forças aplicadas no domínio da estrutura.
10.5 Aproximação do Campo de Tensão
A aproximação do campo de tensão é determinada impondo localmente (ou de maneira forte) a
relação de elasticidade (9) sobre a aproximação (66) do campo de deformação. No entanto, é
mais prático obter esse resultado aplicando a definição matricial (38), ou a definição (68) se se
desejar isolar a contribuição dos deslocamentos nodais:
s =  DBx
 dx 
DB y    = DBx d x + DB y d y
dy 
(71)
Os resultados que se obtêm para o exemplo da placa trapezoidal (estado plano de tensão) são
os seguintes, de acordo com a organização (1) do vector das componentes de tensão, quando se
admite que o módulo de elasticidade é constante e o coeficiente de Poisson ν = 0,3 :
 −40
5E 
DB =
−12
182 
 0
(1)
DB
0
−6
40
0
12
−7
0
0 −20
7 −14 14
 −20 (2 − y )
5E 
=
−6 (2 − y )
182 
 −7 (2 − x)
20 (2 − y )
20 y
(2)
x
6 (2 − y )
7 (1 − x)
6y
−7 (1 − x)
 −6 (2 − x)
5E 
=
−20 (2 − x)
182 
 −7 (2 − y )
6 (1 − x)
−6 (1 − x)
(2)
y
20 (1 − x)
7 (2 − y )
−20 (1 − x)
7y
DB
6
20 
0 
(72)
−20 y 
−6 y 
7 (2 − x) 
(73)
6 (2 − x) 
20 (2 − x) 
−7 y 
(74)
Estes resultados mostram que a aproximação do campo de tensão é constante em elementos
triangulares de 3 nós e linear no elemento rectangular de 4 nós. Mostram, também, que as
componentes do campo de tensão devidas a um deslocamento nodal são em geral não nulas,
devido ao efeito de Poisson.
Os campos de tensão nos elementos 1 e 2 da placa trapezoidal devidos ao deslocamento nodal
d, ver Figura 31, são definidos multiplicando a terceira coluna da matriz (72) por d 3x(1) = d ,
E
σ xx(1) = 0; σ yy(1) = 0; σ xy(1) = ( 35
182 ) d
(75)
e a quarta coluna da matriz (73) por d 4(2)
x =d :
(2)
(2)
30 E
35 E
E
σ xx(2) = (− 100
182 ) ( y ) d ; σ yy = ( − 182 ) ( y ) d ; σ xy = ( 182 ) (2 − x ) d
41
(76)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Estes resultados mostram que a aproximação feita para o campo de deslocamentos está
associada a campos de tensão que são descontínuos ao longo do lado comum dos elementos em
que a placa foi discretizada.
10.6 Equilíbrio do Campo de Tensão no Domínio do Elemento
A aplicação das condições de equilíbrio no domínio, definidas pela equação (13) na forma,



fˆx = −∂ xσ xx − ∂ yσ xy
fˆ = −∂ σ − ∂ σ
y
y
yy
x
em Ω
xy
permite determinar as forças de massa que equilibram o campo de tensões. De acordo com as
definições (8) e (38), a expressão deste resultado é a seguinte,
fˆ = − AT ( DB d ) em Ω
(77)
ou, se se usar a expressão (71):
fˆ = − AT ( DBx d x ) − AT ( DB y d y ) em Ω
É importante notar que estas forças não representam as forças de massa do problema que se
estiver a analisar, f , por exemplo as definidas na Figura 28 para a placa trapezoidal, mas as
forças que equilibram a aproximação feita para o campo de tensões.
O resultado (72) mostra que um elemento de 3 nós só pode equilibrar forças de massa nulas.
Conclui-se, portanto, que no exemplo em análise a condição de equilíbrio no elemento 1 é
sempre violada, independentemente dos valores que se venham a obter para os deslocamentos
nodais do elemento.
Segundo os resultados (73) e (74), a aproximação do campo de tensões num elemento de 4
nós só pode equilibrar forças de massa nulas ou constantes. No entanto, e como adiante se
ilustra, mesmo quando as forças de massa são constantes, como no caso do peso próprio,
verifica-se que a solução obtida aplicando o Método dos Elementos Finitos não satisfaz, em
geral, a condição de equilíbrio no domínio dos elementos.
Exercício 10: Verifique serem as seguintes as forças de massa equilibradas pelo campo de
tensão no elemento 2 da placa trapezoidal devido ao deslocamento nodal d:
fˆx(2) = 0;
fˆy(2) = ( 514E ) d
(78)
10.7 Equilíbrio do Campo de Tensão na Fronteira do Elemento
A aplicação das condições de equilíbrio (23),
 tˆx = nxσ xx + n yσ xy
ˆ
 t y = n yσ yy + nxσ xy
42
em Γ
(79)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
permite determinar as forças que equilibram a aproximação do campo de tensões na fronteira Γ
de um dado elemento. Obtêm-se as seguintes expressões gerais para este resultado usando as
definições (11) e (38) ou (71):
tˆ = N T ( DB d ) em Γ
(80)
tˆ = N T ( DBx d x ) + N T ( DB y d y ) em Γ
(81)
Como os lados dos elementos de 3 e 4 nós são sempre definidos por segmentos de recta, as
componentes da normal exterior unitária, nx e n y , são constantes, concluindo-se que essas forças
são constantes para o elemento de 3 nós e têm uma variação linear para o elemento de 4 nós.
Retomando o efeito do deslocamento d na aproximação feita sobre a placa trapezoidal, de
acordo com os resultados (75) e (76) e com a definição (79), as forças que equilibram esses
estados de tensão ao longo do lado que os elementos partilham são as seguintes para cada
elemento,
 tˆx(1) = (+1) σ xx(1) + (0) σ xy(1) = 0
Γ ( x = 1)  (1)
(1)
(1)
5E
 tˆy = (0) σ yy + (+1) σ xy = ( 26 ) d
(2)
(2)
(2)
100 E
 tˆx = (−1) σ xx + (0) σ xy = ( 182 ) ( y ) d
(2)
(2)
(2)
35 E
 tˆy = (0) σ yy + (−1) σ xy = −( 182 ) d
Γ ( x = 1) 
mostrando que a deformada representada na Figura 31 está associada a campos de tensão que
violam a condição de equilíbrio de forças entre os elementos segundo a direcção x, qualquer que
seja o valor (infinitesimal) do deslocamento nodal, d ≠ 0 ,
(1)
(2)
 tˆx + tˆx ≠ 0
ˆ(1) ˆ(2)
 t y + t y = 0
Γ ( x = 1) 
as quais deveriam ser iguais e de sinal contrário, como em qualquer diagrama de corpo livre, tal
como impõe a condição (27) e se verifica (neste caso particular) para o equilíbrio de forças
segundo a direcção y.
Verifica-se que, em geral, a solução obtida aplicando o Método dos Elementos Finitos não
satisfaz as condições de equilíbrio na fronteira entre elementos. O mesmo se passa na fronteira
estática da malha de elementos finitos, como já se ilustrou na análise da consola triangular (ver
Figuras 12 e 16).
As condições de equilíbrio não são, por isso, impostas de maneira forte (isto é, em todos os
pontos) mas de maneira fraca recorrendo ao conceito de força nodal equivalente, através da
condição de equilíbrio nodal (39). Ilustra-se na Secção 11 a determinação dos termos dessa
equação.
43
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Exercício 11: Verifique serem as forças representadas na Figura 32 que equilibram os campos
de tensão nos elementos 1 e 2 da placa trapezoidal devido ao deslocamento nodal d = 1 :
tx
tˆx(1) =
5
26
4
3
E
1
2
tˆx(1) = − 265 E
3
ty
tˆx(2) = − 100
182 yE
1
4
3
tˆx(1) = − 135 E
1
2
tˆx(1) = 0
200
tˆy(2) = − 182
E
35
tˆy(2) = − 182
E
35
tˆx(2) = 182
(2 − x) E
tˆx(2) = 100
182 yE
35
tˆx(2) = 182
( x − 2) E
a) Forças segundo x
tˆy(2) = 0
2
tˆy(1) = 0
3
1
tˆy(1) =
5
26
2
tˆy(2) = 0
E
b) Forças segundo y
Figura 32: Forças de fronteira em equilíbrio com os campos de tensão
Exercício 12: Verifique que é globalmente equilibrado o sistema de forças aplicadas nos
elementos 1 e 2 da placa trapezoidal devidas ao deslocamento d = 1 . Nota: Para o elemento 2
é necessário considerar a contribuição das forças de massa (78) que equilibram o campo de
tensão no domínio do elemento.
11. Forças Nodais Equivalentes
Prosseguindo para a segunda fase da aplicação do Método dos Elementos Finitos, resumida na
Secção 7, ilustra-se e interpreta-se o cálculo dos termos da matriz de rigidez (40), do vector das
forças nodais equivalentes às forças de massa (42) e do vector das forças nodais equivalentes às
forças de fronteira (43) escritas a nível de elemento.
Usam-se como aplicação os elementos de 3 e 4 nós definidos nas Tabelas 1 e 2, identificandose na Figura 33 as forças correspondentes aos deslocamentos representados na Figura 29.
F3x
F2 y
3
fy
fx
y
F3 y
F4 y
F3 y
1
2
3 F3x
F4 x 4
fy
F2 x
y
F1x
F1 y
F1x 1
F1 y
fx
2 F2 x
F2 y
x
b) Elemento rectangular de 4 nós
x
a) Elemento triangular de 3 nós
Figura 33: Convenção para a medição das componentes do campo de forças
44
Análise de Estruturas II: Elasticidade Plana e Tridimensional
11.1 Vector das Forças Nodais Equivalentes às Forças de Massa
Como adiante se mostra, num elemento triangular de 3 nós as forças nodais equivalentes a forças
de massa constantes,
f x = f x e f y = f y em Ω
(82)
são obtidas calculando as resultantes dessas forças e distribuindo-as uniformemente pelos nós do
elemento, ou seja,
Fix = 13 A f x e Fiy = 13 A f y
(83)
em que A representa a área do elemento. O resultado é análogo para o elemento rectangular de 4
nós, como se ilustra nas Figuras 34 e 35:
Fix = 14 A f x e Fiy = 14 A f y
(84)
Fy
3
fy
fx
2
2
1
y
Fy
3
Fx
1
y
Fx
Fx
Fy
x
b) Forças nodais equivalentes,
Fiα = Fα = 13 A fα
x
a) Forças de massa constantes, fα ,
elemento com área A
Figura 34: Forças nodais equivalentes às forças de massa no elemento de 3 nós
Fy
3
4
Fy
Fx
4
3 Fx
Fx
1
2 Fx
fy
y
1
fx
2
y
Fy
x
Fy
x
b) Forças nodais equivalentes,
Fiα = Fα = 14 A fα
a) Forças de massa constantes, fα ,
elemento com área A
Figura 35: Forças nodais equivalentes a forças de massa no elemento de 4 nós
45
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Aplicando directamente os resultados (83) e (84) e adoptando a identificação das forças
nodais definida na Figura 30, obtêm-se as seguintes expressões para as forças nodais
equivalentes (em kNm −1 ), representadas na Figura 36:
 F1x   0 
F  

 2x   0 
 F3 x   0 
  

 F4 x   0 
(2)
Ff =   = 

 F1 y  −10
 F2 y  −10
  

 F3 y  −10
 F4 y  −10

  
 F1x   0 
F  

 2x   0 
 F3 x   0 
F f(1) =   = 

 F1 y   −20 / 3
 F2 y   −20 / 3
  

 F3 y   −20 / 3
20
3
(85)
4
3
2m
fx =
0
f y = −20
1
fx =
10
10
3
0
f y = −20
1
2
20
3
1
1
20
3
10
2
10
Figura 36: Forças nodais equivalentes às forças de massa da placa trapezoidal
Os resultados (83) e (84) decorrem da aplicação da definição geral (42) do vector das forças
nodais equivalentes às forças de massa. Se se introduzir a partição correspondente às
componentes em x e em y, de acordo com a relação (63),
 Fx 
Ψ T 0   f x 
Ff =   = ∫ 
 dΩ
T 
Ω
 0 Ψ   fy 
 Fy 
obtêm-se as seguintes expressões,
Fα = ∫ Ψ T fα d Ω
Ω
(86)
com α = x ou α = y , ou para cada componente, de acordo com as definições (59) e (62):
Fiα = ∫ Ψ i fα d Ω
Ω
(87)
Exercício 13: Verifique os resultados (83) e (84) para os elementos de 3 e 4 nós usados na
discretização da placa trapezoidal representada na Figura 28 substituindo as definições (64) e
(65) para as funções de aproximação na expressão geral da definição (87), ficando para os
elementos 1 e 2, respectivamente:
46
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Fiα = ∫
1
∫
2x
2
2
2
0
0
0 0
Fiα = ∫
1
2
Ψ i fα dy dx = ∫
0
∫
Ψ i fα dy dx = ∫
∫
1
2
0
y
Ψ i fα dx dy
2
∫Ψ
1
i
fα dx dy
Os resultados (83) e (84) são apenas válidos para forças de massa constantes e para os
elementos caracterizados nas Tabelas 1 e 2. Os resultados serão diferentes se as forças de massa
não forem constantes e/ou as funções de aproximação não forem lineares em elementos
triangulares ou bilineares em elementos rectangulares.
Todavia, o que a definição (87) assegura, para qualquer tipo de elemento e para qualquer
expressão das forças de massa, é que as forças nodais equivalentes realizam sobre os
deslocamentos nodais correspondentes o mesmo trabalho que as forças de massa realizam sobre
a aproximação (59) do campo de deslocamentos no domínio do elemento, ou seja,
diα Fiα = ∫ (Ψ i diα ) fα d Ω = ∫ uα fα d Ω
Ω
Ω
(88)
para o campo devido ao deslocamento nodal diα (nó i, direcção α = x ou α = y ) quando todos
os restantes são nulos.
Exercício 14: Recorrendo à generalização (18), defina o vector das forças nodais equivalentes
a uma variação de temperatura uniforme nos elementos da placa trapezoidal.
11.2 Vector das Forças Nodais Equivalentes às Forças de Fronteira
Se na definição geral (43) do vector das forças nodais equivalentes às forças de fronteira se
introduzir a partição das componentes em x e em y obtêm-se expressões análogas às
determinadas para as forças de massa, com a diferença que são agora definidas sobre a fronteira,
Γ , onde as forças estão aplicadas:
 Fx 
Ψ T 0   t x 
Ft =   = ∫ 
dΓ
T  
Γ
 0 Ψ  ty 
 Fy 
Fα = ∫ Ψ T tα d Γ
(89)
Fiα = ∫ Ψ i tα d Γ
(90)
Γ
Γ
Tal como para as forças de massa, de acordo com a definição (90) uma força de fronteira
aplicada segundo uma dada direcção, x ou y, é substituída por forças nodais equivalentes com a
mesma direcção, Fix ou Fiy . A principal diferença entre as definições (86) e (89) é que as forças
nodais equivalentes às forças de massa são distribuídas por todos os nós do elemento enquanto as
forças nodais equivalentes às forças de fronteira são apenas distribuídas pelos nós contidos no
47
Análise de Estruturas II: Elasticidade Plana e Tridimensional
lado do elemento em que essas forças estão aplicadas. Esta característica resulta da condição (57)
imposta sobre as funções de aproximação, a qual tem como consequência que a função associada
ao nó, i, Ψ i , tem valor nulo nos lados do elemento que não contêm esse nó.
(x3, y3)
y = y1 + b
(x4, y4 )
Ψ1 = γ1 y + β1 x +α1 = 0
x = x1
(x2, y2 )
Ψ2 = γ2 y + β2 x +α2 = 0
(x3, y3)
x = x1 + a
Ψ3 = γ3 y + β3 x +α3 = 0
y
y
(x1, y1)
x
y = y1
(x1, y1)
(x2, y2 )
x
b) Elemento de 4 nós
a) Elemento de 3 nós
Figura 37: Definição das fronteiras dos elementos de 3 e 4 nós
Definem-se na Figura 37 as equações dos lados dos elementos de 3 e 4 nós caracterizados nas
Secções 9.1 e 9.2, respectivamente, para apoiar o cálculo das forças nodais equivalentes a forças
de fronteira. Por exemplo, se no lado definido pelos nós 1 e 4 do elemento de 4 nós estiver
aplicada uma força constante, tα = p , a expressão (90),
Fiα = ∫
y1 + b
y1
(Ψ i p ) x = x
dy
1
produz as seguintes definições para as forças nodais equivalentes, de acordo com os dados da
Tabela 2, em que x ' = x − x1 e y ' = y − y1 :
F1α = ∫
y1 + b
y1
(Ψ 1 p ) x = x
1
F2α = ∫
y1 + b
y1
F3α = ∫
F4α = ∫
(Ψ 2 p ) x = x
1
y1 + b
y1
y1 + b
y1
dy =
1
1
0
b
0
x '= 0
∫ ( x '/ a )( y '/ b )
x '= 0
∫ (1 − x '/ a )( y '/ b )
x '= 0
dy =
dy =
x '= 0
∫ (1 − y '/ b )( x '/ a )
dy =
(Ψ 3 p ) x = x
(Ψ 4 p ) x = x
∫ (1 − x '/ a )(1 − y '/ b )
b
b
0
b
0
p dy ' = 12 pb
p dy ' = 0
p dy ' = 0
p dy ' = 12 pb
Ou seja, a resultante da força aplicada no lado com comprimento b é repartida igualmente
pelos dois nós de extremidade.
Exercício 15: Mostre que se obtém o mesmo resultado para os restantes lados do elemento de
4 nós representado na Figura 37, assim como para qualquer lado do elemento de 3 nós com a
geometria geral definida na mesma figura.
48
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Exercício 16: Determine os vectores das forças nodais equivalentes às forças de fronteira para
as duas discretizações da consola quadrada representada na Figura 38.
y
p (kNm −2 )
Malha 1
4
Malha 2
3
3
2
ν = 0,3
1m
fx = f y = 0
1
x
3
E = const. ( kNm −2 )
1
2
1
2
1m
Figura 38: Consola quadrada sujeita a uma carga uniforme (estado plano de tensão)
Fjx = 13 Rx
Fix = 23 Rx
px
j
i
Rα = 12 pα Lk
Lk
Fjy = 13 Ry
Fiy = 23 Ry
py
i
j
Figura 39: Forças nodais equivalentes a forças de fronteira lineares em lados com 2 nós
Como as funções de aproximação do campo de deslocamentos, Ψ i , variam linearmente ao
longo dos lados dos elementos de 3 e 4 nós, a definição (90) produz o mesmo resultado para a
mesma variação das forças aplicadas, como se ilustra na Figura 39 para forças de fronteira
lineares aplicadas em lados definidos por dois nós. No entanto, essa definição produz diferentes
resultados para elementos baseados em diferentes funções de aproximação, mantendo-se a
condição de definir forças nodais que realizam sobre os deslocamentos nodais o mesmo trabalho
que as forças de fronteira realizam sobre a aproximação dos deslocamentos nessa fronteira:
diα Fiα = ∫ (Ψ i diα ) tα d Γ = ∫ uα tα d Γ
Γ
Γ
10
20 kPa
3
4
1
2
F4 y
3
3
4
1
F3 y
2
1
2
3
F3 y = 13 ( +5) + 23 ( −10) = −5
1
F4 y = 23 ( +5) + 13 ( −10) = 0
2
1
Figura 40: Forças nodais equivalentes às forças aplicadas na fronteira da placa trapezoidal
49
Análise de Estruturas II: Elasticidade Plana e Tridimensional
São as seguintes as expressões dos vectores das forças nodais equivalentes ( kNm −1 ) às forças
de fronteira para o exemplo da placa trapezoidal, as quais estão representadas na Figura 40:
 F1x   0
F  
 2x   0
 F3 x   0
Ft (1) =   = 
 F1 y   0
 F2 y   0
  
 F3 y   0
 F1x   0
F  
 2x   0
 F3 x   0
  
 F4 x   0
(2)
Ft =   = 
 F1 y   0
 F2 y   0
  
 F3 y  −5
 F4 y   0
  






















(91)
11.3 Matriz de Rigidez
Se na definição geral (40) da matriz de rigidez se introduzir a partição correspondente às
partições (68) e (71) das deformações e das tensões devidas às componentes em x e em y dos
deslocamentos nodais obtém-se a seguinte expressão,
 Κ xx Κ xy 
Κ =
 = ∫Ω
Κ
Κ
yx
yy


Β xT 
 T  D Β x
Β y 
Β y  d Ω
verificando-se as seguintes condições de simetria:
T
Kαα = Kαα
= ∫ Β αT D Β α d Ω
Ω
K xy = K yxT = ∫ Β xT D Β y d Ω
Ω
O termo geral da matriz pode ser determinado pela expressão seguinte, devendo ter-se em
conta quais são os deslocamentos envolvidos, segundo x ou segundo y, na identificação das
colunas Β i e Β j da matriz que define as deformações compatíveis com esses deslocamentos:
K ij = K ji = ∫ Β iT D Β j d Ω
Ω
(92)
Por exemplo, o termo K 53 da matriz de rigidez do elemento 1 da discretização da placa
trapezoidal é definido pelas quinta e terceira colunas das matrizes (69) e (72),
K 53 = K 35 = ∫
1
∫ {0
2x
0 0
0
 −6 

5E 
−1 } 182
−20 dy dx
 14 


e o termo K 46 da matriz de rigidez do elemento 2 é definido pelas quarta e segunda colunas das
matrizes (70) e (74), se se usar a partição anteriormente descrita:
50
Análise de Estruturas II: Elasticidade Plana e Tridimensional
K 46 = K 64 = ∫
2
1
∫{−
2
0
1
2
y
1− x }
1
2
0
5E
182
 6(1 − x) 


20(1 − x)  dy dx
 7(2 − y ) 


Exercício 17: Usando um programa de computação simbólica, aplique a definição (40) e os
dados resumidos nas Tabelas 1 e 2 para obter a expressão geral da matriz de rigidez do
elemento de 3 nós,
K ij xx =
G 
κ +1

βi β j 
γi γ j +
4A 
κ −1

(93)
K ij yy =
G 
κ +1

γi γ j 
 βi β j +
4A 
κ −1

(94)
K ij xy = K ji yx =
G 
κ −3

βi γ j 
γi β j −
4A 
κ −1

(95)
e do elemento rectangular de 4 nós, em que β = b/a e α = β 2 (κ + 1)/(κ − 1) :
 2 + 2α

G  1 − 2α
K xx = K yy =
6 β  −1 − α

 −2 − α
1 − 2α
2 + 2α
−2 − α
−1 − α
−1 − α
−2 − α
2 + 2α
1 − 2α
−2 − α 
−1 − α 
1 − 2α 

2 + 2α 
−1 κ − 2
 +1 2 − κ
κ − 2
−1 2 − κ
+1
G 
T
K xy = K yx =
+1 2 − κ 
2(κ − 1)  −1 κ − 2


+1 κ − 2
−1
2 − κ
(96)
(97)
As expressões gerais (93) a (97) para os coeficientes da matriz de rigidez, assim como as
anteriormente dadas para o vector das forças nodais equivalentes, são úteis na aplicação manual
do Método dos Elementos Finitos. Os programas de cálculo baseiam-se em processos mais
gerais e eficazes, sumariamente descritos na Secção 17.
Exercício 18: Particularize os resultados do exercício anterior para obter as expressões das
matrizes de rigidez elementares para o exemplo da consola trapezoidal, definido na Figura 28:
0
0
60 −60 
 400 −400
 −400 435 −35
70 −130
60 

0 −35 35 −70
70
0
E 
K (1) =


0
70 −70 140 −140
0
364 
 60 −130 70 −140 240 −100 


60
0
0 −100 100 
 −60
51
(98)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
65 −5 −65
5
 290 −255 −145 110
 −255 290 110 −145
5 −65 −5 65

 −145 110 290 −255 −65
5 65 −5


5 −65
E  110 −145 −255 290 −5 65
(2)
K =
5 −65
−5 160 −60 −80 −20 
364  65


5
65 −60 160 −20 −80 
 −5 −65
 −65
−5
65
5 −80 −20 160 −60 


5
65
−5 −65 −20 −80 −60 160 

(99)
Tal como o termo independente da equação resolvente (39) combina as forças equivalentes às
forças de massa e de fronteira, o termo geral da matriz de rigidez define as forças equivalentes às
forças de massa (77) e de fronteira (80) que equilibram os campos de tensão provocados pela
aproximação do campo de deslocamentos: K ij representa a força nodal equivalente Fi devida à
acção do deslocamento nodal d j = 1 quando são nulos todos os restantes deslocamentos nodais.
Para demonstrar esta interpretação, introduz-se na definição (40) da matriz de rigidez a
expressão da matriz (37) que define as deformações compatíveis,
K = ∫ (AΨ )T D B d Ω
Ω
e integra-se por partes para obter as forças nodais (42) e (43) equivalentes às forças de massa
(77) e às forças de fronteira (80) provocadas pelos deslocamentos nodais:
K = − ∫ Ψ T (AT D B ) d Ω + ∫ Ψ T (N T D B ) d Γ
Ω
Γ
(100)
Esta interpretação é ilustrada para a deformada definida na Figura 31. Estão representadas na
Figura 41a) as forças equivalentes às forças de massa que equilibram o campo de tensões, nulas
no elemento 1 e dadas pela equação (78) para o elemento 2. As forças equivalentes às forças que
equilibram esse campo de tensões na fronteira dos elementos (ver Figura 32) estão representadas
na Figura 41b). As resultantes dessas forças recuperam os coeficientes da terceira e quarta
colunas das matrizes de rigidez (98) e (99) do elemento 1, d 3(1)x = 1 , e do elemento 2, d 4(2)
x = 1:
 F1(1)
  K13(1) 
 0
x
 (1)   (1) 
 −35 
 F2 x   K 23 


(1) 
 F3(1)




35
K
E



x
33
 (1)  =  (1)  =


 F1 y   K 43  364 −70 
 F2(1)y   K 53(1) 
 70 
 (1)   (1) 


 F3 y   K 63 
 0
 F1(2)
  K14(2) 
 110 
x
 (2)   (2) 
−145 
 F2 x   K 24 


 F3(2)
  K (2) 
−255 
x
34
 (2)   (2) 


 F4 x   K 44  E  290 
 (2)  =  (2)  =


 F1 y   K 54  364  −5 
 F2(2)
  K (2) 
 65 
y
 (2)   64



(2)
5
 F3 y   K 74 

 (2)   (2) 
 −65 


 F4 y   K84 
52
(101)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
5E
28
4
3
1
3
2
1
4
3
5E
28
2
1
3
2
1
2
5E
28
Forças segundo x
5E
28
Forças segundo y
a) Forças nodais equivalentes às forças de massa, Eq. (77)
5E
52
10 E
156
200 E
273
3
−
1
3 − 200 E
273
4
5E
52
− 526E
5E
156
100 E
273
−
5E
52
5E
52
−
1
E
− 100
273
−
10 E
156
− 1591E
4
− 526E
2
− 526E
3
2
5E
26
1
1
5E
26
Forças segundo x
3
2
5E
156
− 1591E
−
2
5E
26
Forças segundo y
b) Forças nodais equivalentes às forças de superfície, Eq. (80)
K 33(1)
(2)
K 44
K 34(2)
4
3
1
(1)
13
K
K 63(1)
3
1
K
(1)
23
(2)
14
K
(2)
K 74
4
3
2
K84(2)
2
1
K
(2)
24
(1)
K 43
Forças segundo x
3
2
1
K 53(1) K 54(2)
2
(2)
K 64
Forças segundo y
c) Coeficientes da matriz de rigidez, Eq. (101)
Figura 41: Forças nodais devidas ao deslocamento d 3(1)x = d 4(2)
x = d na placa trapezoidal
Exercício 19: Verifique e represente o significado físico de uma coluna das matrizes de
rigidez dos elementos de 3 nós da consola quadrada usando os resultados (93) a (95):
0 −35
0 −35
35
 35
 0 100 −100 −30
0
30 

135
30 35 −65
E  −35 −100
K (1) =


30 100
0 −100 
182  0 −30
 −35
0
35
0 35 −35


30 −65 −100 −35 135
 35
53
(102)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
0
0
30 −30 
 100 −100
 −100
135 −35 35 −65
30 

0 −35 35 −35
35
0
E 
K (2) =


0
35 −35 35 −35
0
182 
 30 −65 35 −35 135 −100 


30
0
0 −100 100 
 −30
(103)
Exercício 20: Verifique e represente o significado físico de uma das colunas das matrizes de
rigidez do elemento de 4 nós da consola quadrada aplicando os resultados (96) e (97), e
calcule um coeficiente aplicando a definição (92):
20
65
−5 −65
5
 180 −110 −90
 −110 180
20 −90
5 −65
−5
65

 −90
20 180 −110 −65
5
65
−5 


−5
65
5 −65
E  20 −90 −110 180
(1)
K =
5 −65
−5 180
20 −90 −110 
364  65


5
65
20 180 −110 −90 
 −5 −65
 −65
−5
65
5 −90 −110 180
20 


5
65
−5 −65 −110 −90
20 180 

(104)
Exercício 21: Utilize os resultados (77), (80) e (100) para mostrar que a matriz de rigidez, K ,
define forças nodais equivalentes, K d , que realizam sobre os deslocamentos nodais um
trabalho, d T K d , equivalente ao realizado pelas forças de massa e de fronteira sobre a
aproximação do campo de deslocamentos: d T K d = d T fˆ + d T tˆ .
12. Formulação da Equação Resolvente
Analisa-se a seguir a terceira fase do processo de aplicação do Método dos Elementos Finitos
resumido na Secção 7. Mostra-se que a equação resolvente (46) da malha de elementos finitos é
obtida combinando os vectores das forças nodais e as matrizes de rigidez elementares usando um
processo de reunião análogo ao adoptado na análise de estruturas reticuladas.
12.1 Deslocamentos e Forças Nodais da Malha de Elementos Finitos
A identificação dos deslocamentos nodais independentes de uma malha de elementos finitos, q ,
consiste apenas em seleccionar os movimentos (de translação) livres em cada nó. Esses
deslocamentos, reunidos no vector q e cuja dimensão define o grau de indeterminação
cinemática da malha, β , são medidos no referencial global, pois é nesse referencial que são
definidos os deslocamentos nodais dos elementos. As forças correspondentes definem o vector
das forças nodais, Q .
54
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Os deslocamentos e as forças nodais para o exemplo da placa trapezoidal estão definidos na
Figura 42, sendo portanto β = 5 o grau de indeterminação cinemática para esta discretização
muito grosseira:
q T = { q1
q2
Q T = { Q1 Q2
q4
q3
q5 }
q4
Q5 }
Q3 Q4
q5
q3
Q3
q1
q2
Q5
Q4
Q1
Q2
Figura 42: Deslocamentos nodais independentes e forças nodais correspondentes
No vector das forças nodais distinguem-se as parcelas associadas a cada tipo de carregamento,
designadamente as forças nodais equivalentes às forças de massa, Q f , às forças de fronteira, Qt ,
às tensões ou deformações residuais que possam existir, Qr , para além das forças concentradas
que possam estar aplicadas nos nós da malha, Qn :
Q = Q f + Qt + Qn
(105)
Admite-se aqui que as forças nodais equivalentes a tensões ou deformações residuais, como
por exemplo as deformações térmicas, são incluídas no vector das forças nodais equivalentes às
forças de massa. Essas forças são nulas para o exemplo da placa trapezoidal, assim como as
forças nodais aplicadas, para o carregamento definido na Figura 28.
12.2 Incidência Nodal dos Deslocamentos Indeterminados
Na análise de estruturas reticuladas, para garantir a continuidade dos deslocamentos entre
elementos unidimensionais é suficiente impor que os elementos que partilham um mesmo nó
tenham aí deslocamentos idênticos aos deslocamentos da estrutura (continuidade nodal).
O mesmo acontece na análise de estados planos. Como se mostrou na Secção 10.2, as funções
de aproximação dos elementos bidimensionais são construídas de modo a assegurar que:
• A condição de continuidade nodal é suficiente para assegurar a continuidade dos
deslocamentos entre dois elementos, desde que esses elementos tenham o mesmo número
de nós no lado que partilham.
55
Análise de Estruturas II: Elasticidade Plana e Tridimensional
A segunda condição imposta no processo de reunião de elementos de estruturas reticuladas
consiste em igualar as forças aplicadas num nó da estrutura à resultante das forças nodais dos
elementos que partilham esse nó (equilíbrio nodal). É também esse o critério adoptado em
problemas bidimensionais, mas com uma consequência diferente e importante, já ilustrada na
Secção 10.7 e que adiante se confirma:
• O equilíbrio das forças nodais equivalentes não é suficiente para garantir o equilíbrio entre
os elementos que partilham um mesmo nó.
As operações de reunião de elementos são formalmente descritas pelas condições (44) e (45),
servindo a primeira para identificar os deslocamentos nodais dos elementos considerados
isoladamente com os deslocamentos nodais independentes da malha e a segunda para definir as
forças nodais da malha em função das forças nodais dos elementos. No entanto, é mais prático,
mesmo computacionalmente, realizar estas operações recorrendo a uma tabela que resume a
informação presente nas matrizes de incidência nodal, ℑ .
Essa tabela de incidência é a seguinte para o exemplo da placa trapezoidal, de acordo com a
numeração definida nas Figuras 30 e 42 (admitindo que se numeram sequencialmente as
componentes em x e em y dos deslocamentos e forças nodais dos elementos):
Estrutura ( qi , Qi )
1
2
3
4
5
Elemento 1 ( d i(1) , Fi (1) )
1
2
3
6
-
Elemento 2 ( d i(2) , Fi (2) )
-
1
4
8
7
Tabela 3: Incidência nodal (deslocamentos indeterminados e forças correspondentes)
Tal como para as estruturas reticuladas, esta tabela serve para estabelecer a condição de
continuidade dos deslocamentos nodais e definir a resultante das forças nodais quando se realiza
a ligação dos elementos, recorrendo à informação resumida nas Figuras 30 e 42:
 d1(1) = q1
 (1)
(2)
 d 2 = d1 = q2
(1)
(2)
 d3 = d 4 = q3
 d (1) = d (2) = q
8
4
 6
 d7(2) = q5
(106)
 Q1 = F1(1)

(1)
(2)
 Q2 = F2 + F1
(1)
(2)
 Q3 = F3 + F4
 Q = F (1) + F (2)
6
8
 4
(2)
 Q5 = F7
(107)
56
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Exercício 22: Defina matricialmente a relação (106) na forma (44), para cada elemento, e
verifique que a relação (107) tem a expressão geral (45).
Exercício 23: Defina as tabelas de incidência nodal para a discretização da consola quadrada
representada na Figura 38 adoptando a numeração indicada na Figura 43 para os
deslocamentos e forças nodais.
q4 , Q4
Malha 1
3
3 q2 , Q2
4
q4 , Q4
Malha 2
2
3
1
1
q1 , Q1
2
1
q3 , Q3
q2 , Q2
2 q1 , Q1
q3 , Q3
Figura 43: Deslocamentos nodais independentes e forças nodais correspondentes
12.3 Equação Resolvente
Sendo nulas as forças concentradas aplicadas nos nós da estrutura, para o carregamento definido
na Figura 28,
{ Q1n
Q2 n
Q3n
Q4 n
Q5n } = { 0 0 0 0 0 }
T
aplica-se a definição (107) para determinar as forças nodais equivalentes às forças de massa,
{Q
Q2 f
1f
Q3 f
Q5 f } = { 0 0 0 −50 / 3 −10 }
T
Q4 f
e às forças de fronteira,
{ Q1t
Q2t
Q3t
Q4t
Q5t } = { 0 0 0 0 −5 }
T
de acordo com os resultados (85) e (91), como se ilustra nas Figuras 36, 39, 44 e 45.
F8(2)
f = −10
F6(1)f = − 203
F7(2)
f = −10
4
3
1
F4(1)f
Q3 f
3
2
1
F5(1)f
F5(f2)
Q4 f
Q5 f
Q1 f
2
Q2 f
F6( f2)
a) Nos elementos
b) Na estrutura
Figura 44: Forças nodais equivalentes às forças de massa
57
Análise de Estruturas II: Elasticidade Plana e Tridimensional
F8(2)
t =0
F7(2)
t = −5
4
3
2
1
Q5t
Q3t
3
1
Q4t
Q1t
2
a) Nos elementos
Q2t
b) Na estrutura
Figura 45: Forças nodais equivalentes às forças de fronteira
É a seguinte a resultante (105) das forças nodais equivalentes (ver Figura 42):
{ Q1
Q2
Q3
Q4
Q5 } = { 0 0 0 −50 / 3 −15 }
T
(108)
Para obter os coeficientes K ij da matriz de rigidez da estrutura a partir dos coeficientes K ij( e )
das matrizes de rigidez de cada elemento é necessário recorrer às condições de incidência em
termos de deslocamentos (106) e de forças nodais (107). Essa atribuição é feita atendendo a que
K ij representa a força nodal Qi na estrutura devida ao deslocamento unitário q j e que K ij( e )
representa a força nodal Fi ( e ) no elemento e devida ao deslocamento unitário d j( e ) , concluindo-se
o seguinte para o exemplo em análise (ver Tabela 3):
 K11 = K11(1)

(1)
 K 21 = K 21
(1)
 K 31 = K 31
 K = K (1)
61
 41
 K 51 = 0
 K12 = K12(1)

(1)
(2)
 K 22 = K 22 + K11
(1)
(2)
 K 32 = K 32 + K 41
 K = K (1) + K (2)
62
81
 42
 K 52 = K 71(2)
 K13 = K13(1)

(1)
(2)
 K 23 = K 23 + K14
(1)
(2)
 K 33 = K 33 + K 44
 K = K (1) + K (2)
63
84
 43
(2)
 K 53 = K 74
 K14 = K16(1)

(1)
(2)
 K 24 = K 26 + K18
(1)
(2)
 K 34 = K 36 + K 48
 K = K (1) + K (2)
66
88
 44
(2)
 K 54 = K 78
 K15 = 0

(2)
 K 25 = K17

(2)
 K 35 = K 47 (109)
 K = K (2)
87
 45
(2)
 K 55 = K 77
A equação resolvente (46) para o exemplo da consola trapezoidal é obtida usando os
resultados (108) e (109), para as definições (98) e (99) das matrizes de rigidez elementares:
0 −0.165
0   q1  
0
 1, 099 −1, 099
 −1, 099 1,992 0, 206 0,179 −0,179   q  
0 

  2  

E
0 0, 206 0,893 −0,179 0, 014   q3  = 
0

  

 −0,165 0,179 −0,179 0, 715 −0,165  q4   −16, 667 

0 −0,179 0, 014 −0,165 0, 440   q5  
−5 
(110)
Este processo de reunião dos elementos é fácil de automatizar, sendo executado elemento a
elemento, tal como foi descrito no texto sobre a análise de estruturas reticuladas. Apresenta-se na
Figura 46 a interpretação física da terceira coluna da matriz de rigidez da estrutura.
58
Análise de Estruturas II: Elasticidade Plana e Tridimensional
q3 = 1
K33
a) Deslocamento imposto na malha
d
=1
3
d
(2)
4
2
(1)
K 63
3
K84(2) K 74(2)
(1)
(2) 4
3 K 33 K 44
1
K 23
b) Forças nodais equivalentes
=1
4
1
K 53
K13
(1)
3
K 43
K13(1) 1
2
3 K 34(2)
(1)
(2)
2 K 23 K14 1
(1)
K 43
K 53(1)
(2)
2 K 24
K 54(2) K64(2)
c) Deslocamento imposto nos elementos
d) Forças nodais equivalentes
Figura 46: Contribuição do deslocamento nodal q3 = 1 para a matriz de rigidez da estrutura
Exercício 24: Verifique as seguintes definições da equação resolvente (46) para o exemplo da
consola quadrada definido nas Figuras 38 e 43 resolvido com um elemento de 4 nós,
 0, 4945
 0, 0549
E
 −0,1786

 −0, 0137
0, 0549 −0,1786 −0, 0137   q1   0 
0, 4945 0, 0137
0,1786  q2   0 
 =

0, 0137
0, 4945 −0,3022  q3   0 

0,1786 −0,3022 0, 4945  q4  −0,5 p 
(111)
e com dois elementos de 3 nós:
 0,7416 −0,1923 −0,3571 0,1648  q1   0 
 −0,1923 0, 7416
0,1923
0   q2   0 
E
 =

 −0,3571 0,1923 0, 7416 −0,5495  q3   0 


0 −0,5495 0, 7416   q4  −0,5 p 
 0,1648
(112)
13. Análise da Solução
Depois de resolvida a equação do Método dos Deslocamentos, o resultado obtido é utilizado para
traçar a deformada da estrutura, os campos de tensão e, eventualmente, os campos de
deformação e as reacções de apoio. Estes resultados, determinados na fase de pós-processamento
dos programas comerciais, são apresentados graficamente e, se se desejar, definidos
numericamente em pontos ou em secções da estrutura.
59
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Para ilustrar a fase de análise dos resultados, e retomando o exemplo da placa trapezoidal,
representa-se na Figura 47 a deformada calculada depois de resolver a generalização (110) da
equação do Método dos Deslocamentos (em 10 −8 m ),
{ q1
q2
q3
q4
q5 } = {−7,140 −4,324 −2,360 −18, 77 −25, 79 }
T
(113)
e as forças nodais equivalentes (107) ao carregamento dado.
10
50
3
2,360
18, 77
25, 79
7,140
20 kPa
15
y
4,324
a) Deformada compatível
fx = 0
f y = −20 kNm −3
1
b) Forças equivalentes
2m
x
1
c) Carregamento
Figura 47: Solução da placa trapezoidal discretizada em dois elementos
Ao analisar esta solução, é essencial distinguir os resultados que têm necessariamente de
satisfazer as condições do problema, mesmo que a solução seja aproximada, dos resultados que
podem violar algumas dessas condições, assim como estimar se esse erro é aceitável ou se exige
o refinamento da solução.
13.1 Incidência Nodal dos Deslocamentos Impostos
Na Figura 48 estão identificados os deslocamentos impostos, qi = 0 no exemplo da placa
trapezoidal, e as forças correspondentes, as reacções nodais equivalentes Ri .
Esta informação é utilizada para relacionar esses deslocamentos e reacções com os
deslocamentos e as forças nodais de cada elemento, definidos na Figura 30, obtendo-se a Tabela
4 e as seguintes condições de incidência, complementares das definidas pelas equações (106) e
(107):
 d 2(2) = q1 = 0
 (2)
 d3 = q2 = 0
(1)
 d 4 = q3 = 0
 d (1) = d (2) = q = 0
5
4
 5
(2)
 d6 = q5 = 0
60
(114)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
 R1 = F2(2)

(2)
 R2 = F3
(1)
 R3 = F4
 R = F (1) + F (2)
5
5
 4
 R5 = F6(2)
(115)
Estrutura ( qi , Ri )
1
2
3
4
5
Elemento 1 ( d i(1) , Fi (1) )
-
-
4
5
-
Elemento 2 ( d i(2) , Fi (2) )
2
3
-
5
6
Tabela 4: Incidência nodal (deslocamentos impostos e reacções correspondentes)
R2
q2
R1
q1
q3
q4
R3
q5
R4
R5
Figura 48: Deslocamentos nodais impostos e reacções correspondentes
13.2 Determinação dos Campos de Deslocamento e de Deformação
A informação relativa aos deslocamentos nodais de cada elemento é retirada das equações (106)
e (114) e do resultado (113), obtendo-se (em 10 −8 m ):
d1(1)x   d1(1)   −7,140 
 (1)   (1)  

d 2 x   d 2   −4,324 
d 3(1)x   d (1)   −2,360 
3
 (1)  =  (1)  = 

d
0
 1 y  d4  
d 2(1)y   d5(1)  
0
 (1)   (1)  

d 3 y   d 6  −18, 77 
d1(2)
  d1(2)   −4, 324 
x
 (2)   (2)  
0
d 2 x   d 2  

(2) 
d 3(2)




0
d
x
 (2)   3(2)  

d 4 x   d 4   −2, 360 
 (2)  =  (2)  = 

0
d1 y   d5  
d 2(2)y   d 6(2)  
0
 (2)   (2)  

d 3 y   d 7   −25, 79 
 (2)   (2)  

d 4 y   d8  −18, 77 
(116)
O campo de deslocamento em cada elemento, medido no referencial global, é determinado
substituindo esta informação na aproximação (35) ou (59) em que o elemento se baseia, tomando
a seguinte expressão quando se usa o resultado (64) para o elemento 1,
(1)
 u x = −7,140 + 2,816 x + 0,982 y
 (1)
 u y = −9, 385 y
61
(117)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
e o resultado (65) para o elemento 2:
 u x(2) = −(4,324 − 0,982 y ) (2 − x)
 (2)
 u y = −(5,875 + 3,510 x) y
(118)
Para além de verificarem as condições de fronteira,
(2)
 u (1)
y = u y = 0 para y = 0
 (2)
 u x = 0 para x = 2
estes resultados confirmam também a continuidade dos deslocamentos entre elementos, de
acordo com a condição (26), com a seguinte variação linear (elementos com dois nós por lado):
 u x(1) = u x(2) = −4,324 + 0,982 y para x = 1
 (1)
(2)
 u y = u y = −9,385 y para x = 1
Estas verificações são suficientes para assegurar que a solução é cinematicamente admissível,
pois está associada a um campo de deformações calculado impondo a condição de
compatibilidade (14) sobre as soluções (117) e (118) ou, o que é equivalente, aplicando a
aproximação escrita na forma (36) ou (68), encontrando-se (à escala 10−8 ),
 ε xx(1) = +2,816
 (1)
 ε yy = −9, 385
 γ (1) = +0,982
 xy
(119)
quando se usa o resultado (69) para o elemento 1, e o resultado (70) para o elemento 2:
 ε xx(2) = +4,324 − 0,982 y
 (2)
 ε yy = −5,875 − 3, 510 x
 γ (2) = +0, 982 (2 − x) − 3,510 y
 xy
(120)
Pode verificar-se facilmente que o campo de deformações não é contínuo entre elementos, ao
longo da fronteira x = 1 . Deverá sê-lo na solução exacta pois não há descontinuidades no
material que forma a placa trapezoidal ( E = const. e ν = const. ) nem das forças aplicadas no
domínio, ao longo da fronteira entre elementos. No entanto, a continuidade do campo de
deformações não é uma condição formal de admissibilidade cinemática, pelo que a solução
aproximada que foi determinada é classificada como cinematicamente admissível.
Exercício 25: Sabendo ser a seguinte a solução do sistema de equações (112),
{ q1
q2
q3
q4 } = ( p /E ) {−0, 2423 +0,3150 −1, 4575 −1, 6999 }
T
(121)
trace a deformada da consola quadrada discretizada em dois elementos de 3 nós, verifique as
seguintes expressões para os campos de deslocamento e de deformação,
62
Análise de Estruturas II: Elasticidade Plana e Tridimensional
 u x(1) = +0, 3150 x ( p /E )
 (1)
 u y = −1, 6999 x ( p /E )
 u x(2) = −(0, 2423 x − 0,5773 y ) ( p /E )
 (2)
 u y = −(1, 4575 x + 0, 2423 y ) ( p /E )
 ε xx(1) = +0,3150 ( p /E )
 (1)
 ε yy = 0
 γ (1) = −1, 6999 ( p /E )
 xy
 ε xx(2) = −0, 2423 ( p /E )
 (2)
 ε yy = −0, 2424 ( p /E )
 γ (2) = −0, 9002 ( p /E )
 xy
(122)
e confirme a admissibilidade cinemática da solução.
Comparando a solução definida no exercício anterior com a solução do sistema (111),
{ q1
q2
q3
q4 } = ( p /E ) {−0,9107 +1,1115 −1,9766 −2, 6457 }
T
(123)
conclui-se que a solução obtida discretizando a consola quadrada num elemento de 4 nós
(aproximação bilinear do campo de deslocamentos) é, para o mesmo número de graus de
liberdade, β = 4 , menos rígida (maiores deslocamentos nodais) do que a solução obtida com
dois elementos de 3 nós (aproximação linear). A solução é também cinematicamente
admissível, sendo as seguintes as definições que se encontram para os campos de
deslocamento e de deformação, o qual varia agora linearmente em todo o domínio da consola:
 u x(1) = −(0, 9107 − 2.0222 y ) x ( p /E )
 (1)
 u y = −(1,9766 + 0, 6691 y ) x ( p /E )
 ε xx(1) = −(0,9107 − 2, 0222 y ) ( p /E )
 (1)
 ε yy = −0, 6691 x ( p /E )
 γ (1) = −(1, 9766 − 2, 0222 x + 0, 6691 y ) ( p /E )
 xy
(124)
13.3 Determinação dos Campos de Tensão
O campo de esforços é determinado pela relação de elasticidade (15) ou, o que é equivalente,
pela aproximação escrita na forma (38) ou (71). É a seguinte a expressão que se obtém para o
exemplo da placa trapezoidal quando se recorre aos resultados (73) e (74) (em kPa ):
 σ xx(1) = 0
 (1)
 σ yy = −18, 77
 σ (1) = 0, 76
 xy
 σ xx(2) = +5, 629 − 2,314 x − 2,158 y
 (2)
 σ yy = −10, 061 − 7, 714 x − 0, 647 y
 σ (2) = +0, 755 (2 − x) − 2, 697 y
 xy
(125)
Os resultados correspondentes para a consola quadrada são os seguintes para a discretização
em dois elementos de três nós (aproximação constante),
 σ xx(1) = +0, 3642 p
 (1)
 σ yy = +0,1038 p
 σ (1) = −0, 6538 p
 xy
 σ xx(2) = −0,3462 p
 (2)
 σ yy = −0,3462 p
 σ (2) = −0,3462 p
 xy
63
(126)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
e para um elemento de 4 nós (aproximação linear):
 σ xx(1) = −(1, 0001 + 0, 2206 x − 2, 2222 y ) p
 (1)
 σ yy = −(0,3002 + 0, 7353 x − 0, 6667 y ) p
 σ (1) = −(0, 7602 − 0, 7778 x + 0, 2574 y ) p
 xy
(127)
O processo de convergência ilustrado na Figura 49, obtido por refinamento da malha de
elementos de 3 nós (refinamento-h), mostra que qualquer uma das soluções acima definidas dá
uma aproximação muito grosseira para o campo de tensões na consola. As quatro soluções aí
apresentadas são obtidas com malhas de 289, 1089 4225 e 16641 elementos, envolvendo 512,
2048, 8192 e 32768 nós, respectivamente.
σ xx
σ yy
σ xy
Figura 49: Solução da consola quadrada
13.4 Determinação dos Campos de Forças no Domínio e na Fronteira
As forças de massa que equilibram o campo de tensões determinado pelo Método dos Elementos
Finitos, assim como as forças que o equilibram na fronteira dos elementos, não são
imediatamente disponibilizadas pelos programas comerciais.
64
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Essas forças são a seguir calculadas para os exemplos em análise, aplicando as definições (77)
e (80), para mostrar que, por regra, os campos de tensão determinados pelo Método dos
Elementos Finitos não são estaticamente admissíveis no sentido forte. Violam tanto as condições
de equilíbrio (13) no domínio dos elementos como as condições de equilíbrio (23) na fronteira
estática da malha. E violam também as condições de equilíbrio (27) de forças entre elementos.
−1, 02
tx = 0
tx = ?
fx = 0
−0, 24
tˆx = −1, 22
+1, 00
tx = 0
fˆx = +0, 48
−1, 22
tˆx = +1, 00
+0, 76
tx = 0
Dadas
−0, 02
Calculadas
a) Forças segundo x
t y = −1
+0,37
−0,37
tˆy = +1, 02
fy = 0
ty = ?
ty = 0
−0, 24
fˆy = −1, 44
+0, 02
tˆy = +0, 76
+0,30
ty = 0
Dadas
+1, 04
Calculadas
b) Forças segundo y
Figura 50: Solução da consola quadrada discretizada num elemento de 4 nós ( p = 1 )
Para o exemplo da consola quadrada discretizada num elemento de 4 nós, definido na Figura
40, as forças de massa que equilibram o campo de tensões (127) são:



fˆx = +0, 4779 p ≠ f x = 0
fˆy = −1, 4444 p ≠ f y = 0
Não sendo conhecidas as forças na fronteira cinemática (as reacções no lado encastrado da
consola), apenas se pode verificar o erro da solução na fronteira estática, encontrando-se os
seguintes resultados:
65
Análise de Estruturas II: Elasticidade Plana e Tridimensional
 tˆx = −(1, 2214 − 2, 2222 y ) p ≠ t x = 0
 tˆy = + (0, 0176 − 0, 2574 y ) p ≠ t y = 0
Γ (x = 1) 
 tˆx = −(1, 0176 − 0, 7778 x) p ≠ t x = 0
 tˆy = +(0, 3664 − 0, 7353 x) p ≠ t y = − p
Γ (y = 1) 
 tˆx = + (0, 7602 − 0, 7778 x) p ≠ t x = 0
 tˆy = + (0, 3002 + 0, 7353 x) p ≠ t y = 0
Γ (y = 0) 
Estes resultados estão apresentados na Figura 50, estando os resultados correspondentes
obtidos para a discretização em dois elementos de 3 nós resumidos na Figura 51:
 tˆx = −0,346 p ≠ t x = 0
ˆ
 t y = −0, 346 p ≠ t y = 0
(128)
 tˆx = −0, 654 p ≠ t x = 0
ˆ
 t y = +0,104 p ≠ t y = − p
(129)
 tˆx = +0,346 p ≠ t x = 0
 tˆy = +0,346 p ≠ t y = 0
(130)
Γ (x = 1) 
Γ (y = 1) 
Γ (y = 0) 
Verifica-se que, em ambos os casos, a aproximação é ainda muito fraca pois os sistemas de
forças que equilibram os campos de tensão estão ainda longe de recuperar o carregamento dado
(ver Figuras 38 e 50).
Pelo contrário, e apesar de não se mostrar as escalas de cores para cada componente do campo
de tensão na definição dos campos de tensão apresentada na Figura 49, a análise da solução mais
refinada mostra o seguinte, relativamente às condições de fronteira estáticas do problema,
definidas pelas equações (128) a (130):
• Na face direita (fronteira x = 1 ), as componentes de tensão σ xx e σ xy são constantes e
(praticamente) nulas (t x = σ xx ≈ 0; t y = σ xy ≈ 0) ;
• Na face superior (fronteira y = 1 ), a componente de tensão axial σ yy equilibra a carga
aplicada (t y = σ yy ≈ − p ) e a tensão σ xy é nula (t x = σ xy ≈ 0) ;
• Na face inferior (fronteira y = 0 ), as componentes de tensão σ yy e σ xy são nulas
(t x = −σ xy ≈ 0; t y = −σ yy ≈ 0) .
Não é possível concluir sobre a qualidade da solução do campo de tensões na secção de
encastramento (fronteira cinemática, x = 0 ). No entanto, regista-se já a esperada concentração de
tensões nos cantos dessa secção.
66
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Recordando que o sistema resolvente (46) do Método dos Elementos Finitos não inclui
nenhuma equação que imponha directamente o equilíbrio dos campos de tensão entre elementos,
pois apenas impõe o equilíbrio das forças nodais equivalentes, em ambas as direcções e nos nós
livres da malha, a sequência de resultados apresentada na Figura 49 confirma o que
intuitivamente se espera: à medida que se aumenta o número de nós em que essas condições são
impostas, mais próximo se está de impor as condições de equilíbrio de maneira forte, ou seja, em
todos os pontos do domínio em análise (cerca de 32000 para a solução mais refinada).
tˆx = −0, 654
tˆx = −0, 654
0,346
fˆx = 0
fˆx = 0
0, 707
fˆx = 0
fˆx = 0
0,364 0, 707
0, 364
0, 346
tˆx = +0,346
tˆx = +0,346
Diagrama de corpo livre
Reunião dos elementos
a) Forças segundo x
tˆy = +0,104
tˆy = +0,104
0,346
fˆy = 0
0,346
fˆy = 0
0,536
0,536
fˆy = 0
fˆy = 0
0,654
0, 654
tˆy = +0, 346
tˆy = +0, 346
Diagrama de corpo livre
Reunião dos elementos
b) Forças segundo y
Figura 51: Solução da consola quadrada discretizada em dois elementos de 3 nós ( p = 1 )
As descontinuidades que se observam na definição dos campos de tensão apresentada na
Figura 49 para as duas primeiras soluções correspondem, essencialmente, ao desequilíbrio de
forças entre elementos, como se ilustra na Figura 51.
67
Análise de Estruturas II: Elasticidade Plana e Tridimensional
O mesmo se conclui quando se analisam os resultados relativos à para a placa trapezoidal,
apresentados na Figura 52. As soluções (125) e (126) mostram que o campo de tensões é
descontínuo entre elementos, para x = 1 na placa trapezoidal e para y = x na placa quadrada (ver
Figuras 28 e 38, respectivamente) e não satisfazem a condição mais fraca (mas formalmente
suficiente) de equilíbrio das forças:
(1)
(2)
 tˆx + tˆx ≠ 0
Γ i  (1) (2)
 tˆy + tˆy ≠ 0
tx = 0
4, 64
fx = 0
5,39
1, 00
0,36
tx = 0
(131)
3,32
tx = ?
fˆx = 0
tx = 0
fˆx = 5
3, 32
tˆx = −0, 76
1, 00
0, 76
Dadas
Calculadas
a) Forças segundo x
10
20 kPa
19, 07
9,07
26, 78
5, 04
4, 64
ty = 0
f y = −20
ty = 0
fˆy = 0
fˆy = +1, 4
0, 76 0, 76
ty = ?
17, 76
25, 47
tˆy = +18, 77
Dadas
Calculadas
b) Forças segundo y
Figura 52: Solução da placa trapezoidal discretizada em dois elementos
13.5 Determinação das Reacções de Apoio
As reacções de apoio, na realidade a aproximação que se obtém com uma dada malha de
elementos finitos, são determinadas calculando as forças que equilibram o campo de tensões ao
longo da fronteira cinemática da estrutura.
68
Análise de Estruturas II: Elasticidade Plana e Tridimensional
São disso exemplo as forças na secção de encastramento da consola quadrada definidas nas
Figura 50 e 51 para as discretizações num elemento de 4 nós e em dois elementos de 3 nós.
Relativamente ao exemplo da placa trapezoidal, essas reacções correspondem à força t y ao longo
do bordo y = 0 e à força t x ao longo do bordo x = 2 , representadas na Figura 52.
Os programas comerciais oferecem usualmente a opção de listar as forças nodais na malha de
elementos finitos, designadamente as forças equivalentes nos nós restringidos (geralmente
designadas por reacções de apoio) recorrendo às condições de incidência nodal, como se ilustrou
com a relação (115) para o exemplo da placa trapezoidal. Essa informação pode ser usada para
confirmar o equilíbrio global das forças aplicadas.
O processo mais prático para calcular as forças nodais equivalentes consiste em recorrer à
equação elementar (39), dado que se conhece a matriz de rigidez de cada elemento e, após a
solução do problema, os deslocamentos nodais da malha e, portanto, de cada elemento.
Os resultados para o exemplo da consola trapezoidal, resumidos na Figura 53, são obtidos
recorrendo às definições (98) e (99) das matrizes de rigidez elementares e à solução (116) para
os deslocamentos nodais. Pode verificar-se facilmente que as forças aplicadas a cada elemento e
à malha satisfazem as condições de equilíbrio global: são nulas as resultantes das forças segundo
as direcções x e y, assim como o momento resultante na direcção ortogonal ao plano da estrutura.
9,38
3
7, 29
0,38 0,38
4
0
0, 75
1
16, 67
15, 0
1,94
0
3 1,94
2 0,38 0,38 1
15
0
2 1,94
10,13 11,94
0
1,94
10,35
0, 75
Diagrama de corpo livre
21,97
10,35
Reunião dos elementos
Figura 53: Forças nodais equivalentes para o exemplo da placa trapezoidal
Exercício 26: Determine as forças nodais equivalentes para o exemplo da consola quadrada
discretizada em dois elementos de 3 nós e num elemento de 4 nós e verifique as condições de
equilíbrio global. Utilize os resultados (102) a (104) e as soluções (121) e (123), para além
das condições de incidência nodal.
Exercício 27: Identifique a razão que assegura que as soluções obtidas pelo Método dos
Elementos Finitos sejam globalmente equilibradas.
69
Análise de Estruturas II: Elasticidade Plana e Tridimensional
14. Elementos Isoparamétricos
Ao desenhar malhas de elementos finitos, é necessário utilizar elementos com geometria
irregular, por exemplo, para fazer a transição entre elementos com dimensões diferentes em
zonas com diferentes graus de refinamento. É também importante dispor de elementos com lados
curvos, para representar adequadamente a geometria da estrutura.
Surgem três tipos de dificuldades quando se tenta definir esse tipo de elemento no sistema de
coordenadas global da malha, ou mesmo quando se tenta defini-los em coordenadas locais,
obtidas por translação e/ou rotação do referencial global.
Duas dessas dificuldades têm consequências importantes em termos da eficácia
computacional do método. A primeira é a complexidade das expressões que se obtêm para as
funções de aproximação, sujeitas às condições (57) e (58), a qual cresce substancialmente
quando se aumenta o grau da aproximação e se generaliza a geometria do elemento. Por outro
lado, torna-se inviável definir de um uma maneira computacionalmente eficaz os limites dos
integrais (40), (42) e (43) que definem cada um dos coeficientes da matriz de rigidez e dos
vectores das forças nodais equivalentes presentes na equação resolvente.
No entanto, é a terceira dificuldade que justifica o abandono da ideia, usada nas secções
anteriores, de definir as funções de aproximação no referencial global da malha ou num
referencial local do elemento. Como se ilustra na Figura 54, quando se definem no referencial
global da malha ( x, y ) funções de aproximação de grau superior e se impõem as condições (57)
e (58), essas condições deixam de ser suficientes para garantir que as funções são coincidentes
ao longo do lado partilhado pelos elementos. Deixa de estar assegurada a continuidade dos
deslocamentos entre elementos, uma condição que está na base da formulação do Método dos
Elementos Finitos aqui usada.
s=L
si
y
i
s
Ψ i(1) ( x, y )
Ψ i(2) ( x, y )
1
s=0
s=0
si
s=L
s
x
a) Elementos adjacentes
b) Variação das funções no lado comum
Figura 54: Descontinuidade de funções de aproximação definidas no referencial global
Estas dificuldades são ultrapassadas, com alguns custos computacionais, definindo elementos
com geometria simples (elementos-mestre), sobre os quais se definem de uma maneira fácil e
70
Análise de Estruturas II: Elasticidade Plana e Tridimensional
sistemática as funções de aproximação sujeitas às condições (57) e (58). Como a geometria é
simples, também o é a definição dos limites dos integrais exigidos pela aplicação do método de
cálculo. Nas aplicações bidimensionais são usados dois tipos de elemento-mestre, o triângulo
rectângulo de lado unitário e o elemento quadrado com semi-lado unitário, representados na
Figura 55.
η
η
η = +1
1
1
ξ = −1
ξ = +1
ξ +η = 1
ξ =0
ξ
1
η =0
1
ξ
η = −1
1
1
Figura 55: Elementos-mestre triangular e quadrangular
Para tornar essas definições válidas para elementos com geometria arbitrária, o elementomestre e as funções de aproximação são caracterizados num espaço independente do espaço em
que a malha é definida (espaço das coordenadas naturais). O elemento-mestre é depois mapeado
sobre cada elemento da malha, por exemplo nos representados na Figura 54a), recorrendo a uma
mudança de coordenadas, do sistema de coordenadas naturais (ξ ,η ) para o sistema de
coordenadas da malha de elementos finitos ( x, y ) . É esta a fonte dos custos computacionais
adicionais que resultam desta opção para resolver as dificuldades acima referidas.
Em princípio, é possível usar diferentes expressões para as funções de aproximação e de
mapeamento do elemento-mestre. Um elemento é definido como isoparamétrico quando se usam
as mesmas funções para os dois fins, sendo implicitamente garantida a continuidade dos
deslocamentos entre elementos com os mesmos nós nos lados que partilham.
14.1 Elemento-Mestre
É sobre estes elementos que são definidas as funções de aproximação. Essas funções tomam
expressões relativamente simples, as quais são deduzidas uma única vez para cada grau de
aproximação.
Mantêm-se válidos os critérios definidos na Secção 9, designadamente as condições (57) e
(58), assim como a interpretação aí dada sobre o número total de nós e o número de nós por
fronteira para definir o grau das aproximações no domínio e na fronteira dos elementos-mestre.
71
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Para ilustrar a simplicidade relativa das expressões dessas funções, resume-se na Tabela 5 as
funções de aproximação para elementos triangulares de 3 nós (aproximação linear) e de 6 nós
(aproximação quadrática) representados na Figura 26. As funções de aproximação para os
elementos quadrangulares de 4 nós (aproximação quadrática incompleta) e de 9 nós
(aproximação quártica incompleta) representados na Figura 27 estão definidas na Tabela 6.
Elemento
Ψ1
Ψ2
Ψ3
Ψ4
Ψ5
Ψ6
3 nós
1 − ξ −η
6 nós
(1 − ξ − η ) (1 − 2ξ − 2η )
ξ
η
4ξ (1 − ξ − η )
ξ (2ξ − 1)
4ξ η
η (2η − 1)
4η (1 − ξ − η )
Tabela 5: Elementos triangulares
Elemento
4 nós
9 nós
Ψ1
1
4
(1 − ξ ) (1 − η )
1
4
Ψ2
1
4
(1 + ξ ) (1 − η )
− 12 η (1 − ξ 2 ) (1 − η )
Ψ3
1
4
(1 + ξ ) (1 + η )
1
4
Ψ4
1
4
(1 − ξ ) (1 + η )
ξ η (1 − ξ ) (1 − η )
ξ η (1 + ξ ) (1 − η )
1
2
Ψ5
1
4
Ψ6
ξ (1 + ξ ) (1 − η 2 )
ξ η (1 + ξ ) (1 + η )
1
2
η (1 − ξ 2 ) (1 + η )
Ψ7
− 14 ξ η (1 − ξ ) (1 + η )
Ψ8
− 12 ξ (1 − ξ ) (1 − η 2 )
Ψ9
(1 − ξ 2 ) (1 − η 2 )
Tabela 6: Elementos quadrangulares
0.1
1
0
0.5
-0.1
-1
0
1
0.75
0.5
0.25
0
1
0.5
-1
0
-0.5
-0.5
-0.5
0
0
1 -1
a) Função Ψ 1
1
0.5
0
-0.5
-0.5
0.5
0.5
1
0.75
0.5
0.25
0
-1
-0.5
0
0.5
1
-1
b) Função Ψ 2
1
c) Função Ψ 9
Figura 56: Funções de aproximação do elemento quadrangular de 9 nós
72
-1
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Os gráficos representados nas Tabelas 1 e 2 mantêm-se válidos para as funções de
aproximação dos elementos de 3 e 4 nós, sendo agora definidos no sistema de coordenadas
naturais (ξ ,η ) . Na Figura 56 representam-se três funções típicas do elemento de 9 nós. Pode
confirmar-se que as funções variam quadraticamente (três nós por lado) ao longo dos lados que
contêm o nó onde a função toma valor unitário.
Exercício 26: Trace as funções de aproximação do elemento triangular de 6 nós.
14.2 Mapeamento do Elemento-Mestre
As funções de aproximação formuladas para cada elemento-mestre são usadas para mapear o
elemento em qualquer elemento da malha de elementos finitos (daí a designação alternativa de
funções de forma). Essa mudança de coordenadas é escrita de forma análoga à usada para
aproximar os deslocamentos, definida pela equação (59),
N
x = ∑ Ψ i (ξ ,η ) cix
i =1
(132)
N
y = ∑ Ψ i (ξ ,η ) ciy
i =1
em que cix e ciy representam agora as coordenadas em x e em y, medidas no referencial global da
malha, do nó i do elemento com N nós.
η
4
4
3
η
1
y
ξ
1
1
3
ξ
2m
2
1
1
1
1
1
2
x
Figura 57: Mapeamento do elemento de 4 nós num elemento trapezoidal
Exemplifica-se na Figura 57 o mapeamento do elemento-mestre de 4 nós num elemento com
o domínio da placa trapezoidal, Figura 28. Depois de determinar as coordenadas nodais,
{ c1x
c2 x
c3 x
c4 x } = { 0 2 2 1 }
{c
c2 y
c3 y
c4 y } = { 0 0 2 2 }
1y
e aplicar as expressões definidas na Tabela 6, obtém-se a definição da mudança de coordenadas:
73
Análise de Estruturas II: Elasticidade Plana e Tridimensional
4
x = ∑ Ψ i (ξ ,η ) cix = Ψ 1 ⋅ (0) + Ψ 2 ⋅ (2) + Ψ 3 ⋅ (2) + Ψ 4 ⋅ (1) = 1 + ξ + 14 (1 − ξ ) (1 + η )
i =1
(133)
4
y = ∑ Ψ i (ξ ,η ) ciy = Ψ 1 ⋅ (0) + Ψ 2 ⋅ (0) + Ψ 3 ⋅ (2) + Ψ 4 ⋅ (2) = 1 + η
i =1
É importante frisar que a mudança de coordenadas (132) não é, em geral, invertível. Ou seja,
não é em geral possível determinar univocamente as coordenadas (ξ ,η ) no elemento-mestre de
um dado ponto do elemento com coordenadas ( x, y ) no referencial global da malha.
Como adiante se mostra, esta limitação tem consequências que complicam a implementação
dos elementos isoparamétricos, pois impede que as funções de aproximação sejam expressas no
sistema de coordenadas globais. No entanto, continua a ser computacionalmente mais eficaz
basear o cálculo em coordenadas naturais mesmo quando a mudança de coordenadas é invertível,
por exemplo nos elementos de 3 nós e nos elementos de 4 nós com pelo menos dois lados
paralelos após o mapeamento.
Por exemplo, a mudança de coordenadas (133) tem a inversa,
ξ =4
x −1
; η = y −1
4− y
(134)
a qual em nada simplifica a definição das funções de aproximação do elemento de 4 nós
definidas na Tabela 6, nem a manipulação dessas funções, como adiante se mostra.
Uma outra característica importante, mas esta positiva, é que a mudança de coordenadas (132)
permite representar domínios curvos. Como as funções de aproximação são definidas de modo a
ter grau n − 1 num lado com n nós, o mapeamento permite que um lado de um elemento-mestre
com esse número de nós se transforme numa linha com grau menor ou igual a n − 1 no
referencial da malha.
Uma consequência directa desta conclusão é o caso particular dos elementos triangulares de 3
nós e quadrangulares de 4 nós (ambos com dois nós por lado), os quais só podem ser mapeados
em polígonos de três e quatro lados (rectos), respectivamente.
Exercício 28: Considere o mapeamento do elemento-mestre de 3 nós definido na Figura 26
no elemento triangular de 3 nós definido na Figura 23. Defina e mostre que é invertível a
mudança de coordenadas (132) usando os resultados resumidos na Tabela 5. Mostre que essa
mudança de coordenadas é invertível e use o resultado obtido para recuperar as definições
para as funções de aproximação no sistema de coordenadas globais dadas na Tabela 1.
Um exercício análogo, mas que exige menos esforço de cálculo, consiste em mapear o
elemento-mestre de 4 nós definido na Figura 27 no elemento rectangular de 4 nós definido na
74
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Figura 24 e usar os resultados resumidos nas Tabelas 2 e 6. O exercício seguinte serve para
ilustrar a representação de fronteiras não lineares e a aproximação implícita na mudança de
coordenadas:
Exercício 29: Defina o mapeamento do elemento-mestre de 6 nós definido na Figura 26 no
quarto de círculo representado na Figura 58 e trace sobre o arco de círculo ( x 2 + y 2 = 1) a
aproximação da geometria obtida (mapeamento do lado ξ + η = 1 do elemento-mestre).
η
y
5
5
4
1
4
6
2
1
1
1
6
2
3
ξ
1
1
3
x
Figura 58: Mapeamento do elemento de 6 nós num quarto de círculo
14.3 Aproximação do Campo de Deslocamentos
A aproximação dos deslocamentos continua a ser expressa na forma (59), com a diferença que as
funções de aproximação estão agora definidas no sistema de coordenadas naturais:
N
u x ( x, y ) = ∑ Ψ i (ξ ,η ) d ix
i =1
N
(135)
u y ( x, y ) = ∑ Ψ i (ξ ,η ) d iy
i =1
Para além de se continuar a aproximar independentemente as duas componentes (de
translação) do movimento, mantém-se a hipótese que tanto essas componentes como os
deslocamentos nodais são medidos no referencial da malha de elementos finitos, como se mostra
na Figura 29 para os elementos de 3 e 4 nós. Consequentemente, mantém-se também a
identificação das forças nodais correspondentes (ver Figura 33 para os mesmos exemplos).
Retoma-se na Figura 59 o exemplo da placa trapezoidal admitindo agora que é discretizada
num único elemento isoparamétrico de 4 nós, de acordo com o mapeamento (133), ilustrado na
Figura 56. Para a numeração dos deslocamentos nodais definida na Figura 58 e para as funções
definidas na Tabela 6, a aproximação (135) tem a seguinte expressão:
u x ( x, y ) = Ψ 1 (ξ ,η ) q1 + Ψ 4 (ξ ,η ) q2
u y ( x, y ) = Ψ 4 (ξ ,η ) q3 + Ψ 3 (ξ ,η ) q4
75
(136)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
q3 , Q3
q2 , Q2
4
q2 = 1
q4 , Q4
3
q1 , Q1 1
uy = 0
y
u x =Ψ 4
2
x
b) Efeito do deslocamento nodal q2 = 1
a) Deslocamentos e forças nodais
Figura 59: Discretização da malha trapezoidal num elemento de 4 nós
Se a transformação de coordenadas não for invertível (e é invertível neste exemplo), a
aproximação (136) mostra que não é possível determinar o deslocamento num ponto de
coordenadas ( x, y ) do elemento inserido na malha, mesmo depois de determinar os
deslocamentos nodais qi .
Só é possível escolher um ponto do elemento mestre, por exemplo com coordenadas
(ξ ,η ) = (0, 0) , determinar o ponto correspondente no elemento inserido na malha aplicando a
mudança de coordenadas (132), a que corresponderia neste exemplo o ponto ( x, y ) = (1 + 14 ,1) , e
calcular aí o deslocamento através da aproximação (135), ficando para este exemplo:
u x (1 + 14 ,1) =Ψ 1 (0, 0) q1 + Ψ 4 (0,0) q2 = 14 q1 + 14 q2
u y (1 + 14 ,1) = Ψ 4 (0, 0) q3 + Ψ 3 (0, 0) q4 = 14 q3 + 14 q4
14.4 Aproximação dos Campos de Deformação e de Tensão
As deformações compatíveis com a aproximação (135) do campo de deslocamento são definidas
pela condição (10), ou (14) na forma explícita. Como as funções de aproximação deixam de estar
expressas em coordenadas globais, as opções possíveis são recorrer à inversão da transformação
de coordenadas ou recorrer à derivada da função implícita.
Mesmo quando a mudança de coordenadas tem inversa, a expressão que as funções de
aproximação tomam pode não facilitar o cálculo das derivadas. Para o exemplo do mapeamento
(133) do elemento-mestre de 4 nós num elemento trapezoidal, a inversão (134) da mudança de
coordenadas origina a seguinte expressão para a primeira das funções de aproximação:

Ψ 1 ( x, y ) = y  1 −

x −1 

4− y 
Por isso, esta via é abandonada em favor do processo mais geral, e mais sistemático, de
calcular as derivadas através das expressões, como se mostra adiante:
76
Análise de Estruturas II: Elasticidade Plana e Tridimensional
∂ x Ψ i (ξ ,η ) =
∂Ψ i ∂Ψ i ∂ξ ∂Ψ i ∂η
=
+
∂x
∂ξ ∂ x
∂η ∂ x
∂Ψ i ∂Ψ i ∂ξ ∂Ψ i ∂η
∂ y Ψ i (ξ ,η ) =
=
+
∂y
∂ξ ∂ y
∂η ∂ y
(137)
A aproximação do campo de deformações continua a ser expressa nas formas (36) ou (68). A
correspondente aproximação do campo de tensões é determinada impondo a relação de
elasticidade (9), para estados planos de tensão (15) ou de deformação (16), e expressa nas formas
alternativas (38) ou (71).
14.5 Processamento da Mudança de Coordenadas
Para sistematizar os cálculos exigidos pela mudança de coordenadas (132), define-se a matriz
Jacobiana da transformação,
 ∂x
 ∂ξ
J =
 ∂x
 ∂η

∂y
∂ξ 

∂y
∂η 
(138)
determina-se o seu determinante, o Jacobiano da transformação,
J =| J |=
∂x ∂ y ∂x ∂ y
−
≠0
∂ξ ∂η ∂η ∂ξ
e a inversa da matriz Jacobiana, para obter os termos presentes na definição (137):
 ∂y
 ∂η
J −1 = J −1 
 ∂x
 − ∂η

−
∂y
∂ξ 

∂x 
∂ξ 
(139)
Sendo a seguinte a matriz Jacobiana da transformação inversa,
 ∂ξ
∂x
J −1 = 
 ∂ξ
∂ y

∂η 
∂x 

∂η 
∂ y 
(140)
obtém-se a informação necessária para calcular as derivadas parciais (137),
∂ξ
∂ y ∂η
∂y
= + J −1
;
= − J −1
∂x
∂η
∂x
∂ξ
∂ξ
∂ x ∂η
∂x
= − J −1
;
= + J −1
∂y
∂η
∂y
∂ξ
em que, para a mudança de coordenadas (132):
77
(141)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
∂ x N ∂Ψ i
=∑
cix ;
∂ξ i = 1 ∂ξ
∂ x N ∂Ψ i
=∑
cix
∂η i = 1 ∂η
∂ y N ∂Ψ i
∂ y N ∂Ψ i
=∑
ciy ;
=∑
ciy
∂ξ i = 1 ∂ξ
∂η i = 1 ∂η
O cálculo das derivadas em coordenadas globais (137) não é simples, mas é facilmente
programável depois de tabelar as derivadas das funções nas coordenadas naturais.
São os seguintes os resultados que se obtêm para o exemplo da Figura 57, ver Eq. (133):
J=
J −1 =
1 3 − η
4  1 − ξ
0
1
J = 14 (3 − η )
(142)
0
4  1

3 − η ξ − 1 3 − η 
(143)
Para este exemplo, os resultados (141) e (143) mostram serem as seguintes as expressões das
derivadas (137) das funções de aproximação:
 ∂Ψ i

∂Ψ i
∂Ψ i
(1) +
(0) 
= J −1 
∂x
∂η
 ∂ξ

 ∂Ψ i

∂Ψ i
∂Ψ i
= J −1 
(ξ − 1) +
(3 − η ) 
∂y
∂η
 ∂ξ

(144)
Para assegurar a estabilidade numérica da mudança de coordenadas, é importante garantir que
o Jacobiano da transformação seja positivo em qualquer ponto do domínio do elemento:
J >0
(145)
Esta condição é violada em duas situações típicas. A primeira, ilustrada na Figura 60,
acontece quando não se respeita a sequência da numeração dos nós ao definir o mapeamento
(132) do elemento-mestre. A segunda, ilustrada na Figura 61 para o elemento de 4 nós, sucede
quando o elemento-mestre é mapeado num elemento não convexo, isto é, quando existe um
segmento definido por dois pontos da fronteira que não é interior ao domínio do elemento.
No primeiro caso o Jacobiano é negativo em todos os pontos do domínio, pois tem-se:
x = a η ; y = b ξ ; J = − ab
No segundo caso obtém-se,
J = 18 a [ 2b + (b − a) (ξ + η ) ]
concluindo-se que o Jacobiano é positivo em qualquer ponto do domínio para b > 12 a (elemento
convexo), nulo no nó 3 se b = 12 a e negativo ou nulo em todos os pontos com coordenadas,
78
Análise de Estruturas II: Elasticidade Plana e Tridimensional
(ξ + η ) ≤
2b
a −b
se b < 12 a (elemento não convexo). O resultado (142), obtido para o mapeamento convexo
definido na Figura 57, mostra que o Jacobiano é positivo para qualquer ponto do domínio, ou
seja −1 ≤ ξ ≤ +1 e −1 ≤ η ≤ +1 em todos os elementos isoparamétricos quadrangulares.
η
y
3
2
1
b
3
1
1
2
1
ξ
a
x
Figura 60: Alteração da sequência de identificação dos nós
y
η
4
4
3
1
2
1
3
ξ
ξ +η < α
1
1
1
2
a
(b, b)
2
1
b > 12 a
a
1
1
1
2
a
1
2
a
2
x
Figura 61: Convexidade do mapeamento
Um terceiro aspecto que interessa sublinhar é que o valor do Jacobiano, calculado em
qualquer ponto do domínio, não deve ter valores próximos de zero, pois instabiliza o cálculo da
inversa da matriz Jacobiana (139). Como se mostra a seguir, estas situações ocorrem quando o
mapeamento define elementos muito distorcidos, com áreas tendencialmente nulas.
14.6 Cálculo de Integrais
Para definir a equação resolvente (39) de cada elemento da malha é necessário calcular integrais
de domínio, da forma,
I Ω = ∫ f (ξ ,η ) d Ω
Ω
(146)
por exemplo na determinação da matriz de rigidez (40) e do vector das forças nodais
equivalentes às forças de massa (42) ou a campos de tensão ou de deformação residuais (47).
É ainda necessário calcular integrais de fronteira, da forma,
79
Análise de Estruturas II: Elasticidade Plana e Tridimensional
I Γ = ∫ f (ξ ,η )
Γ
Γ
dΓ
(147)
por exemplo no cálculo do vector das forças nodais equivalentes às forças de fronteira (43) ou da
contribuição (48) de apoios elásticos para a matriz de rigidez do elemento. Na equação (147), a
notação f (ξ ,η )
Γ
representa o valor da função na fronteira em que se realiza a integração.
Uma grande vantagem dos elementos isoparamétricos é que esses integrais não têm de ser
calculados nos elementos mapeados, em que, por norma, seria muito difícil (e
computacionalmente muito ineficaz) definir os limites de integração. São calculados no
elemento-mestre, em que é simples a definição desses limites.
Para calcular integrais de domínio (146) em elementos-mestre quadrangulares,
IΩ = ∫
+1
−1
∫
+1
−1
f (ξ ,η ) J (ξ ,η ) dξ dη
(148)
impõe-se a relação entre elementos de área no elemento mapeado e no elemento-mestre, a qual é
definida pelo Jacobiano da transformação:
dx dy = J d ξ dη
Para definir o Jacobiano da transformação de um lado do elemento mapeado,
ds =
dx 2 + dy 2
dx =
∂x
∂x
dξ +
dη
∂ξ
∂η
dy =
∂y
∂y
dξ +
dη
∂ξ
∂η
explora-se o facto desse lado ter definições simples no elemento-mestre. Os lados de um
elemento quadrangular são definidos pelas equações ξ = ξ = ±1 , com d ξ = 0 , ou η = η = ±1 ,
com dη = 0 , como se pode verificar na Figura 27. O integral de fronteira (147) toma as seguintes
expressões para os lados em que ξ = ξ e η = η , respectivamente:
+1
Iξ = ∫ f (ξ ,η ) J Γ (ξ ,η ) dη
−1
+1
Iη = ∫ f (ξ ,η ) J Γ (ξ ,η ) dξ
(150)
−1
2
2
2
2
J Γ (ξ ,η ) =
 ∂x   ∂ y 
 ∂η  +  ∂η 

ξ 
ξ
J Γ (ξ ,η ) =
 ∂x   ∂ y 
 ∂ξ  +  ∂ξ 
 η 
η
80
(149)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Os integrais de domínio (148) e de fronteira (149) e (150) são calculados numericamente,
aplicando-se normalmente a regra de quadratura de Gauss-Legendre,
M
M
I Ω = ∑∑ f (ξi ,η j ) J (ξi ,η j ) wi w j
i =1 j =1
M
Iξ = ∑ f (ξ ,ηi ) J Γ (ξ ,ηi ) wi
i =1
M
Iη = ∑ f (ξi ,η ) J Γ (ξi ,η ) wi
i =1
em que ξi e η j definem os M pontos de integração e wi e w j os pesos correspondentes (os
quais estão definidos no texto sobre Análise de Estruturas Articuladas).
O número de pontos de integração é escolhido atendendo ao grau das funções integrandas,
admitindo que são polinomiais. Tal só sucede para o caso particular de mudanças de coordenadas
isomorfas, em que o Jacobiano é constante.
Quando isso não acontece, o caso mais frequente, as funções integrandas não são polinomiais,
sendo consequentemente aproximado o resultado dessas integrações. Esse facto é ilustrado pelo
resultado (144), lembrando-se que essas derivadas intervêm na definição da matriz (37) de
aproximação do campo de deformação, presente, por exemplo, no cálculo da matriz de rigidez
(40) do elemento.
No caso de elementos triangulares o integral de domínio (148) toma a seguinte expressão (ver
Figura 26),
IΩ = ∫
1 1−ξ
∫
0 0
f (ξ ,η ) J (ξ ,η ) dη dξ
(151)
sendo as expressões (149) e (150) válidas para os lados do elemento-mestre triangular definidos
pelas condições ξ = ξ = 0 e η = η = 0 , com limites de integração [ 0, 1] :
1
Iξ = ∫ f (0,η ) J Γ (0,η ) dη
0
1
Iη = ∫ f (ξ , 0) J Γ (ξ , 0) dξ
0
(152)
(153)
No lado η = 1 − ξ esse integral toma a seguinte expressão:
+1
Iη = ∫ f (ξ ,1 − ξ ) J Γ (ξ ,1 − ξ ) dξ
0
2
J Γ (ξ ,η ) =
2
 ∂x ∂x   ∂ y ∂ y 
 ∂ξ − ∂η  +  ∂ξ − ∂η  para η = 1 − ξ

η 
η
81
(154)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Estes integrais são também calculados numericamente. Existem diferentes regras de
quadratura para domínios triangulares, aplicáveis ao cálculo dos integrais (151). Os integrais de
fronteira (152) a (154) são ainda calculados pela regra de quadratura de Gauss-Legendre.
15. Traçado de Malhas de Discretização
Os programas de elementos finitos incluem rotinas que permitem decompor domínios com
topologias e geometrias complexas em subdomínio mais simples, os quais são discretizados em
malhas de elementos (de facto, células) triangulares ou quadrangulares.
Essas rotinas baseiam-se em considerações topológicas e procuram gerar malhas regulares,
formadas por elementos com formas e dimensões semelhantes, sem transições abruptas em
forma e em dimensões. Todavia, esse objectivo nem sempre é adequadamente atingido, pois a
lógica em que se baseiam não é facilmente generalizável.
Para além disso, essas rotinas são geralmente desenvolvidas sem atender ao problema que vai
ser dessa maneira discretizado, nem à técnica de solução adoptada na sua solução. Ou seja, e no
presente contexto, as malhas são traçadas sem atender às zonas do domínio estrutural onde se
esperam grandes gradientes (concentrações) de tensões, onde é necessário refinar a discretização.
Para além disso, não reconhecem os potenciais problemas numéricos associados à mudança de
coordenadas quando se usam elementos isoparamétricos. É por isso importante analisar a malha
gerada automaticamente e verificar se essas condições estão adequadamente asseguradas.
Figura 62: Esquemas de transição no refinamento de malhas de elementos finitos
Os problemas associados à instabilização da mudança de coordenadas (Jacobianos negativos
ou próximos de zero) são evitados rejeitando (ou corrigindo, se o programa o permitir) malhas
com elementos não convexos ou excessivamente distorcidos. Alguns programas permitem
refinar localmente as malhas, ilustrando-se na Figura 62 esquemas de transição usados no
refinamento de subdomínios triangulares e quadrangulares em elementos triangulares e
quadrangulares.
Na Figura 63a) ilustra-se uma primeira decomposição do domínio na análise de um provete de
betão fendilhado, simplesmente apoiado e sujeito a uma força concentrada. Na Figura 63b)
82
Análise de Estruturas II: Elasticidade Plana e Tridimensional
ilustra-se um primeiro refinamento da malha, com o qual não é ainda possível recuperar os
campos de tensão ilustrados na Figura 64, os quais representam as concentrações de tensões que
se desenvolvem na vizinhança da ponta da fenda e das cargas pontuais. Ilustra-se também na
Figura 64b) o forte efeito de descentrar a posição da fenda.
P
A
20
80mm
120
120
a) Decomposição do domínio
b) Refinamento da malha
Figura 63: Discretização do modelo de provete de betão
Distribuição da tensão σxx
Distribuição da tensão σyy
Distribuição da tensão σxy
b) Fenda descentrada
a) Fenda a meio-vão
Figura 64: Campos de tensão no provete de betão fendilhado
83
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Para facilitar o refinamento local das malhas, alguns programas disponibilizam elementos de
transição, elementos que compatibilizam os graus de aproximação usados em dois ou mais
elementos com diferentes graus de aproximação, ou seja com um número diferente de nós por
lado ou face. Por exemplo, um elemento com dois nós por lado (variação linear) é
compatibilizado com um elemento com três nós no lado comum (variação quadrática)
restringindo os deslocamentos no nó intermédio de modo a ser linear a variação do deslocamento
nesse lado do elemento. Para o exemplo da Figura 65, esta técnica consiste em obrigar os
deslocamentos do nó j a tomar o valor médio dos deslocamentos dos nós de extremidade do lado,
os nós i e k.
k
j
i
Figura 65: Transição entre elementos com dois e três nós por lado
16. Elasticidade Tridimensional
A formulação do Método dos Elementos Finitos anteriormente apresentada para a análise de
problemas de Elasticidade Plana (Estados Planos de Tensão e Estados Planos de Deformação) é
directamente generalizável à solução de problemas tridimensionais. Os principais aspectos dessa
generalização para a análise de sólidos elásticos são a seguir resumidos.
16.1 Variáveis
As variáveis continuam a ser organizadas em pares duais (variáveis estáticas e variáveis
cinemáticas correspondentes), de modo a preservar as definições dadas na Secção 4 para o
trabalho realizado pelas forças interiores e exteriores. De acordo com a notação aí usada, Ω
representa o domínio (volume) do corpo tridimensional e Γ a fronteira (superfície).
Os campos de tensão e de deformação são agora definidos por seis componentes
independentes das nove componentes dos tensores (simétricos) de tensão e de deformação,
s T = { σ xx σ yy
e T = { ε xx
σ zz σ xy σ xz σ yz }
ε yy ε zz γ xy γ xz γ yz }
(155)
(156)
sendo três as componentes necessárias para caracterizar as forças de massa e de fronteira, assim
como os deslocamentos correspondentes:
84
Análise de Estruturas II: Elasticidade Plana e Tridimensional
f T = { fx
fy
fz}
(157)
t T = { tx
ty
tz }
(158)
uT = { u x
uy
uz }
(159)
Todas as variáveis são medidas no referencial global da malha de elementos finitos.
σ zz
σ zx
dz
dx
σ zy
σ xz
σ xx
σ xy
σ yz
σ yx
Fronteira Γ
tz , uz
z
tx , ux
ty , uy
σ yy
y
x
Domínio Ω
dy
Figura 66: Convenção adoptada na medição de variáveis
16.2 Equações
A forma explícita das equações de equilíbrio (8) e de compatibilidade (10) é a seguinte:
 ∂ xσ xx + ∂ yσ xy + ∂ zσ xz + f x = 0

 ∂ yσ yy + ∂ xσ xy + ∂ zσ yz + f y = 0 em Ω
∂ σ +∂ σ +∂ σ + f =0
x xz
y yz
z
 z zz
 ε xx = ∂ x u x
ε = ∂ u
y y
 yy
 ε zz = ∂ z u z

 γ xy = ∂ y ux + ∂ x u y
 γ xz = ∂ z u x + ∂ x u z

 γ yz = ∂ z u y + ∂ y u z
em Ω
(160)
Quando estas relações são escritas matricialmente, de acordo com a organização
anteriormente definida para os vectores de tensão (155) e de deformação (156), e para os
vectores de forças (157) e de deslocamentos (159), obtendo-se a seguinte generalização para os
operadores diferenciais de compatibilidade e de equilíbrio,
 ∂x
0

0
A=
∂y
 ∂z

 0
0
∂y
0
∂x
0
∂z
85
0 
0 
∂z 

0 
∂x 

∂ y 
Análise de Estruturas II: Elasticidade Plana e Tridimensional
 ∂x

A = 0
 0

T
0
0
∂y
∂z
∂y
0
0
∂z
∂x
0
0
∂x
0

∂z 
∂ y 
(161)
mantendo-se a relação que caracteriza a análise baseada na hipótese de linearidade geométrica.
A forma explícita das condições de equilíbrio (11) na fronteira estática e de compatibilidade
(12) na fronteira cinemática é a seguinte,
 nxσ xx + n yσ xy + nzσ xz = tx

 n yσ yy + nxσ xy + nzσ yz = ty
nσ +nσ +nσ =t
x xz
y yz
z
 z zz
 ux = ux

 uy = uy
u =u
z
 z
em Γ t
em Γ u
em que nx , n y e n y continuam a representar as componentes da normal exterior unitária à
fronteira, no ponto da superfície em que estão aplicadas a força com componente tx , ty e tz ,
sendo u x , u y e u z as componentes impostas do vector de deslocamento.
Na formulação matricial da condição de equilíbrio (11) na fronteira, a matriz de equilíbrio
continua a ser análoga à matriz de equilíbrio no domínio, substituindo a componente da normal
unitária exterior o operador diferencial correspondente (161):
 nx

N T = 0
0

0
0
ny
nz
ny
0
0
nz
nx
0
0
nx
0 

nz 
n y 
A matriz de rigidez local, presente na relação de elasticidade (9), toma a seguinte expressão
para materiais homogéneos e isotrópicos,
 λ + 2µ
 λ

 λ
D=
 0
 0

 0
λ
λ
λ
0
0
0
0
0
0
0
0
0
0
0
0
µ
0
0
0
µ
0
0
0
µ
λ + 2µ
λ
λ + 2µ
0
0
0









(162)
de acordo com a ordenação dos vectores de tensão (155) e de deformação (156), em que λ e µ
são as constantes de Lamé:
86
Análise de Estruturas II: Elasticidade Plana e Tridimensional
λ=
νE
(1 + ν ) (1 − 2ν )
E
2 (1 +ν )
µ =G =
16.3 Funções de Aproximação
O cálculo continua a ser baseado em elementos isoparamétricos, sendo agora os elementosmestre o tetraedro recto, com aresta unitária, e o hexaedro cúbico, com semi-aresta unitária,
como se ilustra na Figura 67. As funções de aproximação continuam a ser polinómios
construídos de maneira a satisfazer as condições (57) e (58):
 1 se j = i
 0 se j ≠ i
Ψ i (ξ j ,η j , ζ j ) = 
N
∑Ψ
i =1
i
(ξ ,η , ζ ) = 1
ζ
ζ
1
1
2
2
ξ
η
1
η
ξ
2
b) Elemento hexaédrico
a) Elemento tetraédrico
Figura 67: Elementos-mestre tridimensionais
1
ξ
η
ξ2
ξη
ζ
ξζ
ηζ
η2
ξ3
ξη
2
ζ2
ξζ 2
ζ3
ξη 2
η
3
η 2ζ
ηζ 2
Figura 68: Pirâmide de Pascal
87
Análise de Estruturas II: Elasticidade Plana e Tridimensional
O número de nós do elemento está relacionado com o grau de aproximação, sendo ainda
válidas as identificações apresentadas na Secção 9, recorrendo agora à pirâmide de Pascal
representada na Figura 68, definida em termos das coordenadas naturais (ξ ,η , ζ ) .
As funções de aproximação do elemento tetraédrico de 4 nós (linear) e do elemento
hexaédrico de 8 nós (trilinear) representados na Figura 69 são as resumidas na Tabela 7.
Elemento
Ψ1
4 nós
1 − ξ −η − ζ
8 nós
1
8
(1 − ξ ) (1 − η ) (1 − ζ )
1
8
(1 + ξ ) (1 − η ) (1 − ζ )
1
8
(1 + ξ ) (1 + η ) (1 − ζ )
1
8
(1 − ξ ) (1 + η ) (1 − ζ )
Ψ5
1
8
(1 + ξ ) (1 − η ) (1 + ζ )
Ψ6
1
8
(1 + ξ ) (1 − η ) (1 + ζ )
Ψ7
1
8
(1 + ξ ) (1 + η ) (1 + ζ )
Ψ8
1
8
(1 − ξ ) (1 + η ) (1 + ζ )
Ψ3
ξ
η
Ψ4
ζ
Ψ2
Tabela 7: Elementos tetraédricos e hexaédricos
ζ
ζ
5
4
6
ξ
7
η
1
2
8
1
3
2
η
a) Elemento tetraédrico
4
ξ
3
b) Elemento hexaédrico
Figura 69: Elementos isoparamétricos de 4 e 8 nós
Tal como para os elementos planos, a aproximação é, em geral, completa nos elementos
tetraédricos e incompleta nos elementos hexaédricos. Por exemplo, e de acordo com a Pirâmide
de Pascal, a aproximação é quadrática completa no elemento tetraédrico com 3 nós por aresta
(tetraedro de 10 nós), sendo cúbica incompleta (apenas contém o termo trilinear ξηζ ) no
elemento hexaédrico de 8 nós (a componente quadrática é também incompleta, pois não contém
os termos ξ 2 , η 2 e ζ 2 , sendo apenas completa a componente linear, com a presença dos quatro
primeiros termos da Pirâmide de Pascal). Interessa também notar que as definições das funções
de aproximação nas faces dos elementos tetraédricos e hexaédricos contêm as funções de
aproximação dos elementos planos correspondentes.
88
Análise de Estruturas II: Elasticidade Plana e Tridimensional
16.4 Aproximações
Os elementos isoparamétricos tridimensionais continuam a ser caracterizados por usarem as
mesmas funções de aproximação para mapear o elemento-mestre no elemento inserido na malha
de discretização,
N
x = ∑ Ψ i (ξ ,η , ζ ) cix
i =1
N
y = ∑ Ψ i (ξ ,η , ζ ) ciy
(163)
i =1
N
z = ∑ Ψ i (ξ ,η , ζ ) ciz
i =1
e para aproximar independentemente cada componente do campo de deslocamento:
N
u x ( x, y, z ) = ∑ Ψ i (ξ ,η , ζ ) d ix
i =1
N
u y ( x, y, z ) = ∑ Ψ i (ξ ,η , ζ ) d iy
(164)
i =1
N
u z ( x, y, z ) = ∑ Ψ i (ξ ,η , ζ ) diz
i =1
Os termos (cix , ciy , ciz ) na definição (163) caracterizam as coordenadas do nó i do elemento,
medidas no referencial global da malha. Na definição (164) os termos u x , u y e u z identificam as
componentes de deslocamento medidas no mesmo referencial e expressas em função das
componentes dos deslocamentos nodais, (dix , d iy , diz ) .
É a seguinte a expressão geral da matriz das funções de aproximação na definição matricial
(35), de acordo com a definição (159) do vector dos deslocamentos:
Ψ 1
Ψ =  0
 0
⋯ ΨN
⋯
⋯
0
Ψ1
0
0
0
⋯
0
0
⋯ ΨN
⋯
0
0
Ψ1
0 
⋯
0 
⋯ Ψ N 
⋯
A definição (37) mantém-se válida para a definição (36) das deformações compatíveis com a
aproximação do campo de deslocamentos, ficando,
 ∂ xΨ 1
 0

 0
B=
 ∂ yΨ 1
 ∂ zΨ 1

 0
⋯
⋯
∂ xΨ N
0
∂ yΨ 1
⋯
⋯
⋯
⋯
0
0
∂ yΨ N
∂ zΨ N
0
∂ xΨ 1
0
∂ zΨ 1
0
⋯
⋯
⋯
⋯
⋯
⋯
89
0
∂ yΨ N
0
∂ xΨ N
0
∂ zΨ N
0
0
⋯
⋯
∂ zΨ 1
0
∂ xΨ 1
∂ yΨ 1
⋯
⋯
⋯
⋯
0 
0 
∂ zΨ N 

0 
∂ xΨ N 

∂ yΨ N 
(165)
Análise de Estruturas II: Elasticidade Plana e Tridimensional
de acordo com a condição de compatibilidade (160) e a organização (156) do vector das
componentes de deformação. Também se mantém válida a definição (38) para a aproximação do
campo de tensão, usando agora a matriz de rigidez local (162).
Recorre-se à generalização da regra de diferenciação (137) para calcular os coeficientes da
matriz de compatibilidade (165),
∂ x Ψ i (ξ ,η , ζ ) =
∂Ψ i ∂Ψ i ∂ξ ∂Ψ i ∂η ∂Ψ i ∂ζ
=
+
+
∂x
∂ξ ∂ x
∂η ∂ x ∂ζ ∂ x
∂ y Ψ i (ξ ,η , ζ ) =
∂Ψ i ∂Ψ i ∂ξ ∂Ψ i ∂η ∂Ψ i ∂ζ
=
+
+
∂y
∂ξ ∂ y
∂η ∂ y ∂ζ ∂ y
∂ z Ψ i (ξ ,η , ζ ) =
∂Ψ i ∂Ψ i ∂ξ ∂Ψ i ∂η ∂Ψ i ∂ζ
=
+
+
∂z
∂ξ ∂ z
∂η ∂ z
∂ζ ∂ z
tomando a matriz Jacobiana da transformação (138) a seguinte expressão:
 ∂x
 ∂ξ

 ∂x
J =
 ∂η
 ∂x
 ∂ζ

∂y
∂ξ
∂y
∂η
∂y
∂ζ
∂z 
∂ξ 
∂z 
∂η 
∂z 
∂ζ 
A matriz inversa é calculada numericamente, em cada ponto,
 ∂ξ
∂x

 ∂ξ
J −1 = 
∂ y
 ∂ξ

 ∂z
∂η
∂x
∂η
∂y
∂η
∂z
∂ζ 
∂ x 
∂ζ 

∂y
∂ζ 

∂z 
mantendo-se os cuidados a ter no mapeamento do elemento-mestre nos elementos da malha de
discretização, para garantir a estabilidade das operações decorrentes da transformação de
coordenadas.
16.5 Equação Resolvente
A equação resolvente para um elemento tridimensional mantém a expressão geral (39),
continuando igualmente válidas as definições (40) para a matriz de rigidez e as definições (42) e
(43) para os vectores das forças nodais equivalentes às forças de massa e de fronteira. Também
continua válida a definição (47) para o vector das forças nodais equivalentes a campos de tensão
ou de deformação residuais, e a definição (48) para a contribuição de apoios elásticos para a
matriz de rigidez do elemento.
90
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Todos estes integrais são calculados numericamente. Para elementos hexaédricos, os integrais
de domínio (146) e (148) são substituídos pelos seguintes,
I Ω = ∫ f (ξ ,η , ζ ) d Ω = ∫
Ω
+1
−1
+1
+1
−1
−1
∫ ∫
f (ξ ,η , ζ ) J (ξ ,η , ζ ) dξ dη dζ
ou, numericamente:
M
M
M
I Ω = ∑∑∑ f (ξi ,η j , ζ k ) J (ξi ,η j , ζ k ) wi w j wk
i =1 j =1 k =1
É semelhante a generalização do cálculo de integrais de domínio para elementos tetraédricos.
Relativamente aos integrais de fronteira, são calculados nas faces desses elementos, tendo
portanto expressões análogas às dos integrais de domínio definidas para os elementos planos.
Após o cálculo dos termos da equação resolvente para cada elemento da malha de
discretização, aplica-se o processo de espalhamento anteriormente descrito para determinar os
termos correspondentes da equação resolvente (46) do modelo da estrutura em análise,
recorrendo a tabelas de incidência nodal análogas às anteriormente descritas para problemas
planos. A única diferença é que essa incidência é agora estabelecida para três componentes de
deslocamento e de força em cada nó da malha.
Em consequência da concepção em que se baseiam os elementos isoparamétricos, a condição
(44) de continuidade dos deslocamentos nodais assegura a continuidade de cada componente do
campo de deslocamentos nas interfaces dos elementos. Para além disso, o equilíbrio das
resultantes das forças nodais dos elementos que partilham um mesmo nó, definidas pela
condição (45), continua a caracterizar a função da equação resolvente (46).
Tal como para os problemas unidimensionais (estruturas articuladas e reticuladas) e para
problemas bidimensionais (estados planos de tensão e de deformação), a aproximação do campo
de deslocamentos em sólidos permite obter soluções aproximadas que são compatíveis mas que,
por regra, violam todas as condições de equilíbrio, tanto no domínio como na fronteira dos
elementos. A equação resolvente (46), ao estabelecer o equilíbrio das forças nodais equivalentes,
assegura que se obtém a melhor solução possível (em termos energéticos) com a aproximação
assumida para o campo de deslocamentos.
17. Utilização de Programas
As três grandes fases da análise de uma estrutura pelo Método dos Elementos Finitos foram
anteriormente caracterizadas e ilustradas na solução de exemplos de aplicação: a fase de préprocessamento, em que se recolhem e armazenam os dados sobre a estrutura e o carregamento, e
se define a malha de discretização e o tipo de elemento; a fase de processamento, em que se
91
Análise de Estruturas II: Elasticidade Plana e Tridimensional
determina a equação resolvente de cada elemento da malha, se atribuem esses coeficientes ao
sistema resolvente da malha e se determina de solução do problema; e a fase de pósprocessamento, em que se caracteriza a resposta da estrutura ao carregamento dado, através da
representação da deformada e dos campos de tensão.
A execução dessas operações exige o recurso a técnicas específicas que visam a optimização
de cada fase do cálculo, para minimizar as exigências de armazenamento da informação, para
acelerar as operações e para assegurar a estabilidade numérica do processo de cálculo. Não são
essas técnicas, que quem deseje desenvolver ou adaptar um programa de elementos finitos deve
conhecer, que a seguir se descrevem.
O que se pretende é resumir a informação mais importante para apoiar a utilização de um
programa de elementos finitos, dando-se especial atenção às fases em que tem de existir, ou deve
existir, uma intervenção directa do utilizador, designadamente na definição dos dados e do
modelo de elementos finitos e, principalmente, de análise dos resultados.
Os programas comerciais partilham a mesma estrutura em termos de concepção mas podem
optar por diferentes estratégias na sequenciação de algumas operações. Todavia, o que mais os
distingue são os níveis de sofisticação que permitem na representação de geometrias e de acções,
na caracterização dos materiais estruturais e na selecção de modelos de análise. Incluem,
tipicamente, análises física e/ou geometricamente lineares, em regime estático ou dinâmico,
podendo ou não modelar a interacção entre a estrutura, a fundação e o carregamento.
Para além das potencialidades e das limitações do método e dos modelos de cálculo em que se
baseia, a boa utilização de um programa de elementos exige muita experimentação e o
conhecimento das consequências de cada uma das opções que o utilizador tem de tomar durante
o processo de análise. São essas opções que adiante se abordam, ainda que de uma maneira
muito limitada, de iniciação à utilização de programas de elementos finitos, pois uma informação
mais detalhada só pode ser apresentada no contexto de um dado programa e para um tipo
específico de análise estrutural.
17.1 Caracterização da Análise
Em consequência da generalidade conceptual do Método dos Elementos Finitos, que mais não é
do que um método de solução numérica de problemas às derivadas parciais, a maioria dos
programas oferece a possibilidade de resolver diferentes tipos de problemas definidos pelo
mesmo tipo de equações, designadamente da mecânica de estruturas, de fundações e de fluidos,
ou da térmica ou acústica, e, muitas vezes, o acoplamento desses problemas.
92
Análise de Estruturas II: Elasticidade Plana e Tridimensional
Por isso, a primeira informação a prestar é o tipo de problema (de análise estrutural) que se
pretende resolver. A segunda é sobre o modelo de análise a adoptar, em consequência das
simplificações que se podem alcançar atendendo à geometria das peças e às características do
carregamento. Em consequência da concepção do Método dos Elementos Finitos, esta segunda
informação é dada definindo (ainda em termos gerais) os graus de liberdade dos nós da malha,
isto é, as componentes do deslocamento e da rotação dos nós que podem ser não nulas.
Esta decisão do utilizador, ainda independente dos elementos a usar na análise, condiciona
todo o processo de cálculo, pelo que não pode ter dúvidas sobre os graus de liberdade de cada
tipo de peça estrutural que será utilizado e as acções a que estará sujeito. Um elemento
unidimensional poderá ter de dois a seis graus de liberdade por nó, as translações de um
elemento de treliça com comportamento plano e as três translações e as três rotações de um
elemento de pórtico com comportamento tridimensional, respectivamente. O mesmo sucede com
elementos planos, correspondendo o primeiro a um elemento para estados planos de tensão ou de
deformação e o segundo a um elemento de casca.
É também nesta fase de entrada de dados que se define o tipo de análise estrutural,
designadamente se é uma análise estática ou dinâmica, e se é geometricamente linear
(deformações e deslocamentos infinitesimais) ou não linear (grandes deformações e/ou
deslocamentos).
Dependendo das potencialidades e da flexibilidade do programa, pode ser necessário definir
ainda nesta fase outros aspectos da análise, podendo uns ser do âmbito da concepção do modelo
estrutural e outros do âmbito do processamento numérico. São exemplos a modelação de tensões
ou de deformações residuais, os métodos de armazenamento da matriz do sistema resolvente e de
solução desse sistema, assim como opções específicas sobre execução de determinados tipos de
análise, designadamente análises dinâmicas ou que envolvam a modelação da interacção da
estrutura com a fundação ou com a acção, por exemplo em problemas de acústica estrutural e de
aerodinâmica estrutural.
17.2 Caracterização da Geometria
Apesar da caracterização da geometria estar muito facilitada nos programas comerciais, esta fase
continua a ser a que consome mais tempo na intervenção do utilizador. A estratégia mais
recomendada é a de decompor o domínio em subdomínios com geometrias simples e, se
possível, que ocorram com alguma frequência, tanto no problema que se pretende analisar como
nos tipos de problemas frequentemente analisados.
93
Análise de Estruturas II: Elasticidade Plana e Tridimensional
É importante conceber cuidadosamente a definição de cada subdomínio, pois uma
sistematização adequada facilita substancialmente as fases seguintes de caracterização do
material estrutural e das condições de fronteira do problema. Para além disso, permite criar
ficheiros de dados que podem ser usados em análises posteriores.
A geometria desses subdomínios é caracterizada definindo as coordenadas dos nós
estritamente necessários para definir os elementos que a caracterizam, designadamente
segmentos, superfícies e volumes, consoante o tipo de aplicação. É em geral possível
sistematizar a caracterização de elementos geométricos através de expressões analíticas simples.
Esses dados são definidos separadamente, para apoiar a reunião dos subdomínios,
designadamente os segmentos ou as superfícies comuns em geometrias planas ou
tridimensionais.
17.3 Caracterização do Material Estrutural
Os programas permitem a utilização de uma grande variedade de modelos para as relações
constitutivas, designadamente modelos elásticos, elastoplásticos e viscoelásticos. Podem incluir
diferentes tipos de anisotropia e de não linearidade, dependendo do nível de deformação e/ou da
evolução das propriedades mecânicas no tempo ou, por exemplo, com a temperatura.
Alguns programas permitem que seja o utilizador a criar (ou seja, a programar) um
determinado modelo constitutivo. No entanto, a tendência é para cada programa se especializar
num determinado tipo de material estrutural, tipicamente para estruturas metálicas ou para
estruturas de betão armado pré-esforçado, caso em que disponibilizam os modelos definidos nos
regulamentos que lhes são específicos e nas condições aí definidas.
17.4 Caracterização das Condições de Fronteira
É na caracterização do carregamento e, principalmente, nas condições de apoio que ocorrem com
mais frequência os erros de utilização de programas de elementos finitos.
Para além da representação gráfica desses dados nem sempre ser suficientemente clara, é fácil
confundir o referencial em que os dados são definidos, no referencial global da estrutura ou nos
referenciais locais dos elementos geométricos a que as cargas ou as condições de apoio serão
atribuídos.
A definição das forças aplicadas e das condições de apoio também devem ser tipificadas por
grupos, para depois facilitar a sua atribuição aos elementos usados na caracterização da
geometria, designadamente, pontos, segmentos e superfícies.
Para além de forças (momentos) e de deslocamentos (rotações) impostos em pontos, os
programas definem um conjunto de opções fixas que traduzem os carregamentos e as condições
94
Análise de Estruturas II: Elasticidade Plana e Tridimensional
de apoio usadas com mais frequência. Está também generalizada a oferta da opção de fixar a
posição relativa de pontos da estrutura ligando-os por bielas (ou planos) rígidos.
No entanto, é muito variável a flexibilidade que os programas oferecem para a caracterização
de forças e de deslocamentos variáveis no espaço (e no tempo, em análises dinâmicas), o mesmo
sucedendo em relação à modelação de apoios deformáveis (por exemplo apoios elásticos) ou
unidireccionais (que apenas resistem a forças de contacto), com ou sem atrito.
Tal como para a caracterização dos materiais estruturais, os programas que se especializam
em determinado tipo de solução estrutural incluem os modelos regulamentares que lhes são
específicos, tanto em termos de acções como de condições de apoio.
17.5 Caracterização da Malha de Discretização
A definição de subdomínios com geometrias simples facilita a geração de malhas regulares, com
uma transição progressiva na forma e nas dimensões das células, que posteriormente serão
identificadas com os elementos finitos. Para além disso, o cuidado posto na definição dos
elementos geométricos de interface (os segmentos ou superfícies que são partilhados por
subdomínios) facilita a regularização e a compatibilização das malhas definidas para cada
subdomínio.
Os programas oferecem diferentes opções para gerar as malhas de discretização dos diferentes
subdomínios definidos na análise. Todas elas visam assegurar um determinado nível de
densidade da discretização, podendo escolher-se diferentes critérios de segmentação (tipicamente
leis de progressão aritmética ou geométrica) e escolher dimensões mínimas e máximas. É
também possível escolher o tipo de célula, triangular (tetraédrica) ou quadrangular (hexaédrica)
e, com alguma frequência, o algoritmo de geração da malha.
É essencial analisar criticamente as malhas obtidas antes de avançar para a escolha do tipo de
elemento a utilizar no cálculo. Devem ser rejeitadas as malhas que apresentem distorções fortes
ou incompatibilidades, e deve-se assegurar que é suficiente o refinamento nas zonas do modelo
em que se esperam grandes concentrações de tensões ou esforços.
Só depois se deve escolher o tipo de elemento finito a adoptar na análise. Tem de ser do tipo
especificamente desenvolvido para o modelo estrutural em análise, deve ser coerente com as
células da malha de discretização e deve ter um grau de aproximação adequado à densidade da
malha que foi criada.
Por coerência com as células da malha entende-se que devem ser usados elementos com a
mesma topologia, triangulares ou quadrangulares. Quando se usa este último tipo de elemento
numa malha com células triangulares, ou se opta pelo inverso, está-se implicitamente a introduzir
95
Análise de Estruturas II: Elasticidade Plana e Tridimensional
uma distorção sistemática dos elementos finitos. O mesmo se aplica, naturalmente, a malhas
tridimensionais definidas por células tetraédricas/hexaédricas, as quais devem ser implementadas
com elementos do mesmo tipo.
É óbvia a necessidade de usar o tipo de elemento finito adequado ao modelo estrutural da
peça, designadamente elementos triangulares ou quadrangulares com dois graus por nó para
estados planos de tensão ou de deformação e com três graus de liberdade por nó para estados
tridimensionais. É também intuitivo que não devem ser usadas malhas relativamente grosseiras
com elementos com poucos nós ou que pode ser excessivo usar malhas muito densas com
elementos com muitos nós.
No entanto, e antes de se começar a conhecer razoavelmente um dado programa, é frequente a
dúvida sobre os elementos a utilizar na modelação, especialmente na análise de lajes e cascas,
finas ou espessas em ambos os casos. Há uma gama de elementos disponíveis bastante vasta,
podendo serem distintos os tipos de elementos disponibilizados por diferentes programas. É
indispensável consultar o manual do programa e seguir as recomendações aí dadas sobre a
adequabilidade de cada tipo de elemento para os diferentes tipos de análise.
Concluída a caracterização da malha de discretização de cada subdomínio e a escolha dos
elementos finitos a adoptar, é importante representar a malha e activar a opção que permite
sobrepor os elementos utilizados para verificar a compatibilidade da malha em termos de
incidência nodal. Apesar da solução obtida com uma malha incompatível não ser
necessariamente pior que a obtida com uma malha compatível, deixam de estar garantidas as
condições de convergência da formulação, as quais é importante garantir para poder ajuizar,
posteriormente, se será necessário refinar essa solução.
Para potenciar a sistematização da definição de geometrias e malhas, os programas permitem
importar e combinar ficheiros em que esses dados estão caracterizados, podendo pôr-se o
problema de compatibilizar malhas e elementos. Como se referiu anteriormente, os programas
podem disponibilizar elementos de transição para facilitar essa compatibilização.
17.6 Análise da Solução
Concluída a caracterização do modelo de elementos finitos, processa-se a montagem do sistema
resolvente e o cálculo da solução (ou das soluções em cada incremento em análises dinâmicas
e/ou não lineares). Essa informação é registada em ficheiros, assim como a informação adicional
que o utilizador possa solicitar, tipicamente a energia de deformação, os deslocamentos em
determinados nós e as tensões ou as deformações em determinados pontos (tipicamente os
pontos de Gauss, onde o erro é minimizado) de determinados elementos.
96
Análise de Estruturas II: Elasticidade Plana e Tridimensional
É indispensável analisar cuidadosamente os resultados obtidos para responder a duas questões
essenciais: se o problema resolvido corresponde ao que se pretendia analisar e, em caso
afirmativo, se o nível de precisão obtido é adequado para os fins dessa análise.
Essa decisão é fundamentada combinando dois conjuntos de informação: as condições de
fronteira do problema, pois o carregamento e as condições de apoio são dados do problema; as
condições de aproximação em que o método de cálculo se baseia, pois sabe-se quais as
condições que devem ser satisfeitas localmente e quais as que são impostas de maneira
aproximada. Os comentários seguintes pressupõem uma análise elástica linear, pois podem ser
diferentes as condições impostas de maneira exacta em problemas baseados noutras hipóteses.
No contexto da análise elástica linear, a solução obtida tem de ser estritamente compatível. É
desnecessário verificar se as deformações são compatíveis com a aproximação dos
deslocamentos pois essa condição é implícita à formulação do método de cálculo. Todavia é
necessário verificar se o campo de deslocamentos é contínuo e se satisfaz as condições de apoio
do problema dado.
Essa verificação faz-se facilmente analisando a deformada da estrutura. Terá havido erro do
utilizador na definição da malha de discretização ou na escolha dos elementos finitos se se
verificarem vazios ou sobreposições entre elementos da malha. E terá havido erro do utilizador
na definição das condições de apoio se estiverem livres movimentos que deveriam estar
restringidos, ou se se verificar o inverso.
É também desnecessário verificar se as relações de elasticidade são impostas localmente, pois
está também implícito na formulação que as tensões são calculadas a partir da aproximação do
campo de deformações impondo essas relações. O que deve ser cuidadosamente verificado é o
erro nas condições de equilíbrio no domínio e na fronteira dos elementos, as quais se sabe serem
impostas apenas de maneira aproximada, através do equilíbrio das forças nodais equivalentes. A
facilidade com que essas condições podem ser avaliadas depende muito da sofisticação do
programa de elementos finitos.
Tal como se fez nos exemplos de aplicação, é possível determinar e representar graficamente
o campo das forças de massa que equilibram as tensões calculadas e compará-las com as forças
de massa dadas para avaliar a qualidade do equilíbrio. Também como se fez nesses exemplos, é
possível calcular e representar graficamente as forças de fronteira que equilibram esse campo de
tensões e verificar o desequilíbrio de forças entre elementos e em relação às forças de fronteira
definidas no carregamento (as condições de fronteira estáticas do problema).
97
Análise de Estruturas II: Elasticidade Plana e Tridimensional
No entanto, o que todos os programas disponibilizam é suficiente para avaliar o equilíbrio da
solução e os eventuais erros na definição do carregamento. Todos os programas disponibilizam
representações gráficas dos campos de tensão, estando sempre presentes duas opções: a
representação das tensões calculadas e a representação da regularização dessa solução (sendo
esta opção designada por smoothing, averaging ou regularization). Os programas disponibilizam
também, em modo numérico ou gráfico, as reacções de apoio (de facto, as forças nodais
equivalentes correspondentes aos deslocamentos restringidos), as quais podem ser usadas para
avaliar se o carregamento foi correctamente definido.
A representação do campo de tensões não regularizado serve sempre para decidir sobre a
inadequabilidade da solução. O nível de convergência é necessariamente insatisfatório se as
descontinuidades no campo de tensão são tais que reflectem a malha de elementos finitos usada
no cálculo. Esse resultado deve servir, no entanto, para decidir como melhorar a solução,
refinando as zonas onde os maiores desequilíbrios se verificam. Pode também servir para expor
zonas de concentração de tensões que não haviam sido consideradas na fase de definição da
malha de discretização.
Devem ser feitas duas verificações quando se obtêm campos praticamente contínuos na
representação não regularizada das componentes de tensão. A primeira é confirmar se as tensões
equilibram as forças de fronteira do problema. Se tal não suceder, terá havido erro na definição
do carregamento. A segunda verificação a fazer é sobre as concentrações de tensão reveladas
nessa solução. Se essas concentrações não podem ser justificadas pelo carregamento (cargas
pontuais ou descontínuas), pelas descontinuidades das condições de apoio ou da geometria
(tipicamente cantos reentrantes), ou por restrições impostas sobre o movimento relativo de nós
da malha (tipicamente bielas rígidas), é muito provável que tenha havido erro nas restrições
postas sobre os graus de liberdade dos nós da malha.
É aceitável uma solução que satisfaça os critérios de análise acima resumidos. No entanto, e
como a maioria dos programas não disponibiliza estimadores de erro, se a aplicação exige um
nível de segurança mais apertado, a única opção possível é realizar estudos de convergência, os
quais podem ser feitos sobre a mesma malha e melhorando a qualidade dos elementos, refinando
local ou globalmente a malha ou mesmo gerando uma malha diferente. Para cada um desses
casos traça-se a variação da energia de deformação (disponibilizada pela maioria dos
programas), de deslocamentos nodais representativos e de tensões em elementos mais sensíveis.
Ao analisar esses resultados é necessário notar que a energia de deformação tende a convergir
mais rapidamente que os deslocamentos e estes mais rapidamente que as tensões.
98
Análise de Estruturas II: Elasticidade Plana e Tridimensional
18. Conclusão
Baseando-se na mesma formulação do Método dos Elementos Finitos, os conceitos fundamentais
que a seguir se resumem repõem os já identificados na análise de estruturas articuladas e
reticuladas. De facto, o único conceito fundamentalmente diferente que foi introduzido nesta
generalização do método para a solução de problemas planos e tridimensionais foi o conceito de
elemento isoparamétrico, o qual também é utilizado no contexto das peças lineares:
• Definem-se elementos com geometria simples num espaço independente daquele em que
se realiza a análise da estrutura, os elementos-mestre triangulares/tetraédricos ou
quadrangulares/hexaédricos, definidos no espaço das coordenadas naturais;
• A estrutura é decomposta em elementos finitos isoparamétricos, os quais se caracterizam
por usar o mesmo conjunto de funções para mapear o elemento-mestre nos elementos da
malha de discretização da estrutura e para aproximar a variação do campo de
deslocamentos nesses elementos;
• Essas funções, cujo grau de variação é determinado pelo número de nós do elemento, são
contínuas e definidas de maneira a facilitar a imposição das condições de fronteira
cinemáticas e de continuidade dos deslocamentos entre elementos;
• A aproximação das componentes de deformação é calculada impondo localmente a
condição de compatibilidade no domínio do elemento e a aproximação das componentes de
tensão é calculada impondo localmente a condição de elasticidade, transferindo-se o erro
da aproximação para as condições de equilíbrio no domínio e na fronteira do elemento;
• Essas condições são impostas exigindo apenas o equilíbrio dos nós do elemento,
recorrendo-se à definição de forças nodais estaticamente equivalentes para obter a equação
resolvente elementar, cujos coeficientes são calculados por integração numérica no espaço
do elemento-mestre;
• As equações resolventes elementares são combinadas para obter a equação resolvente do
modelo de elementos finitos, sendo essa combinação determinada por critérios de
incidência nodal que identificam os deslocamentos nodais dos elementos com os
deslocamentos nodais da estrutura e definem, implicitamente, as forças nodais da estrutura
como as resultantes das forças nodais dos elementos;
• A solução que se obtém é (necessariamente) cinematicamente admissível e recupera
(necessariamente) a solução exacta do problema sempre que a aproximação em cada
elemento permita obter uma solução que é aí estaticamente admissível;
99
Análise de Estruturas II: Elasticidade Plana e Tridimensional
• Quando tal não sucede, as condições de equilíbrio no domínio e na fronteira desses
elementos são violadas localmente mas impostas de maneira fraca, através de uma
condição de equilíbrio imposta sobre as forças nodais equivalentes, as quais satisfazem
(necessariamente) as condições de equilíbrio global da estrutura, mesmo que a solução não
seja exacta;
• Uma solução aproximada pode ser sempre melhorada, convergindo para a solução exacta
(a qual geralmente não tem expressão analítica) quando se subdivide os elementos
(refinamento-h), se aumenta o grau da aproximação em cada elemento (refinamento-p), ou
se combinam os dois processos.
100