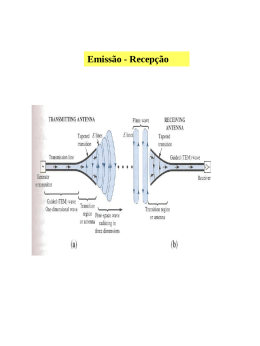
1
2
-
_ e jkrq
^
E 
I q f D ( , ) e
~ q rq
~
Agregados de
Antenas
z
E q r0  jk  rq r0  I q
 e
E 0 rq
I0
jkyq cos I q
e
I0
Iq
I0
 aq  Aqe j q
n jky cos
F   aq e q
q 1
^
r  r  yq cos e
~ q ~0
~r
r
~0
0=
1
Ө

••
• • • •
(q)
y
(n)
x
Ψ – ângulo que a direcção de
observação faz com o eixo ao longo do
qual estão distribuidas as antenas do
agregado.
^ ^
cos   y . e  sin  sin 
~ ~r
4
Espaçamentos comensuráveis
yq  (q 1)d
Fases progressivas
Iq
 a q  A q e jq
I0
a q  A q e j( q 1) 
Factor complexo do agregado
n
F  F ( )  F (  2 )   Aq e j ( q 1)
q 1
  kd cos  
• O factor do agregado é uma função periódica (periodo 2π)
da variável γ.
5
Construção gráfica para obter a forma do diagrama de radiação de
um agregado a partir do Factor (espacial) do agregado
I1         I 2  I1
d /z


| F | cos cos 
2

n
F   aq e jkd (q 1) cos 
q 1
aq  e j (q 1)
Seja   0, n  2
    kd cos 
kd cos 
kd cos 
2
F  1  e jkd cos   e
cos
2
j
 Fm  cos

2
7
Fm ()  Fm 
8
Agregado de radiação longitudinal
D=0.45 δ=kd=0.9π
δ=0.9π
Iq  1e j( q 1) 0.9 
9
Agregado de radiação longitudinal
Woodyard-Hansen
D=0.35 → kd=0.7π
δ=0.9π
Iq  1e j(q1)0.9
10
11
PROE Rad1 130306
Antenas de recepção
Polarização
• A polarização de uma antena é a polarização da onda radiada
pela antena numa dada direcção
• A ponta do vector do campo eléctrico instantâneo traça uma
figura no tempo – este fenómeno designa-se polarização do
campo eléctrico
Abertura efectiva
•A abertura efectiva da antena é uma medida de habilidade da
antena em colectar potência duma onda incidente e fornece-la aos
seus terminais
• Devido à desadaptação de polarizações a potência extraída pela
antena de recepção a partir do sinal incidente não é máxima. Dizse que há perdas de polarização.
PROE Rad7 030406
Polarizações
Polarização
linear
vertical
Polarização
linear
horizontal
Polarização
circular
direita
Polarização
circular
esquerda
Polarização
elíptica
direita
Polarização
elíptica
esquerda
A polarização de uma antena é a polarização da onda
radiada pela antena numa dada direcção.
PROE Rad7 030406
Dipolo eléctrico de Hertz
DEH em modo de recepção
Abertura efectiva
. Seja Ei amplitude do campo eléctrico incidente no
dipolo de comprimento L << 
Ei2
S
2Z 0
( Ei L) 2 sin 2 
1 Ei L sin 
PL 
Rr 
2 Z a 2  Z a*2
8 Rr
Rr  80(L /  ) 2
Ae 2 
PL
3

( sin  ) 2
S 8
m 
2
3
4
G ( )  sin 2   2 Ae ( )
2

Relação fundamental das antenas
G ( ,  ) 
4

2
Ae ( ,  )
PROE Rad7 030406
Em recepção
V 0  h .E
*
~e ~
• he determina a amplitude complexa da tensão induzida em vazio
na antena por um campo
incidente segundo uma direcção (Ө,φ).
Comprimento efectivo – DEH
I
0
 I(0)

^
h  L sin  e
h e  L sin 
~
~e
^
h
~ eM
Dipolo eléctrico de Hertz
 Le
h eM  L
~
f D (, )  sin 
Em condições ideais
Cp=1

Ө=Ө0
φ=φ0

V02  L2 E 2  S  E 2 / 2 Z 0  2 Z 0 SL 2
V02
V02
2 Z 0S
PL 

 L
8R a
8R r
4R r
32
2 S 3   
 L
S
  
4 2  L 
8
2
PL
32
Ae 

S
8PROE Rad7 030406
Relações entre parâmetros característicos
Analisando a ligação entre duas antenas a trabalhar alternadamente
nos regimes de emissão e recepção, a aplicação do Princípio da
reciprocidade permite concluir que o coeciente entre o ganho G e a
área Ae é constante para qualquer antena.
G
 const ant e
Ae
Dípolo eléctrico de Hertz.
G
3  32 

   
Ae
2  8 
1
 4 
  2  const ant e universal
 
Em outras antenas verifica-se:
G
Nas condições ideais,
4
Ae
2
C=1,Ө=Ө0, φ=φ0 tem-se:
V02  h e2 E 2  2h e2 Z0S  PL  SA e   2h e2 Z0
PL
Ae


V02
Y02
2
V   PL 
, R r  R a   2h e Z0 
8
R
8R r A e
a


2
0

 h e2 Z0
2 G
4
V   A e 
, G  D  
V02 2

4

4
R

D



r
2
0
Z h 
D 0  e
Rr   
2
 Z0  h e 

 
D Rr   
Este resultado é generalizável a outras situações
PROE Rad7 030406
2
a) Condições óptimas de recepção
Comprimento efectivo heM
V0=Ei heM
E
V
~i
~ 0
ZL=Za*
Pr=<S>AeM
S
Area efectiva AeM
a) Caso geral
^
Z0 e  jkr
E  j
I 0 h eMf D () e
~ 
~
2 r
Pr  5  A e (, )C p
h e (, )  h eMf D (, )
V0  E i h e (, ) C p
E
V0
~i
E
~a
Cp=1 (antenas coplanares)
V0  E a L  E i L sin 
PROE Rad7 030406
Exemplo
^ 
Antena de emissão com polarização linear  e~ y 
 
Antena de recepção com polarização • esquerda
2
*
h e.E
Cp 
__
h
~ e
__
h
~ e
~
~
2
2
E
2
h *e E

. ~
he E
^
~
~E
~
~
^
 cos 4 5º e  sin 4 5º e
Cp 
^ *
 h e.e
j90 º
~x
^
1 ^
 ^
 e  je
 *.e
~y 
~y
2  ~x
2

^
1 ^

ey 
e  je 

~
~y 
2 ~x
^
1
2
• Metade da potência é perdida
• Nos casos em que esta perda de potência não é tolerada tenta fazer-se
as duas antenas ou com polarização linear vertical ou ambas com
polarização • esquerda
• Mas há situações em que é preferível operar com uma antena linear e
outra circular.
• Por ex. Se num veículo (satélite) espacial uma antena tem
polarização linear devido a rotação de Faraday na ionosfera seria mais
adequado usar uma antena receptora com polarização circular.
PROE Rad7 030406
PROE Rad7 030406
Polarização
• A polarização de uma antena de emissão na direcção (Ө,φ) é a
polarização da onda electromagnética radiada na zona distante
cujo vector de onda k está alinhado com (Ө,φ).
• A polarização de uma antena de recepção na direcção (Ө,φ) é a
polarização da onda electromagnética incidente com o vector de
onda k alinhado (Ө,φ) que, para idênticas intensidades de
iluminação (módulo do associado vector médio de Poynting)
maximiza a potência disponível na antena de recepção (maximiza
a tensão induzida nos terminais, em vazio).
• Em geral a polarização da antena de recepção não é a mesma
que a polarização da onda recebida (incidente), isto é há
desadaptação de polarizações.
• Quando, em recepção, a polarização da onda incidente coincide
com a polarização da antena de recepção (situação ideal) diz-se
que há adaptação de polarizações.
PROE Rad7 030406