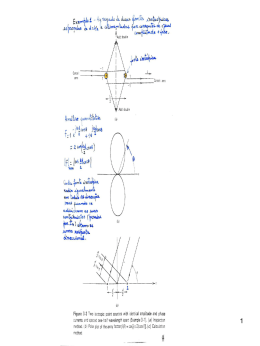
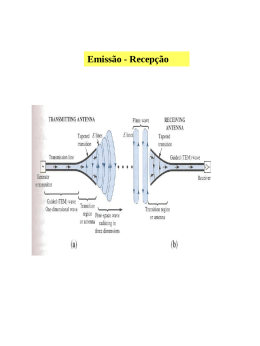
CFI – Aula 4
Polarização de ondas electromagnéticas
PROE CFI Aula4 090306
Polarização
•
•
Comportamento temporal do vector campo eléctrico num ponto fixo do espaço
Exemplo: onda plana e uniforme a propagar-se segundo Z
^
^
~
~
E Ex x  Ey x
~
^
^
~
~
H Hx x  H y y
~
__
•E
__
y ou E x
 onda polarizada linearmente em
^
x e em y
~
__
, respectivamente.
~
__
• Ey e Ex
faz
^
≠ 0 e em fase
O campo eléctrico resultante tem uma direcção que
com o eixo dos xx:
__
arc t g
Ey
__
Ex
PROE CFI Aula4 090306
__
__
• Ey e Ex não estão em fase
_
_
__
E z   E
~
~ 0
e  jkz
Num ponto qualquer do espaço (z=0):
E 0, t   Er co s t  Ei sin t
~
Polarização
circular
__
^
^

E  x  j y  E0
~

~
~

^
^
^
^



E 0, t   E0 x co s t  y sin t  E x x  E y y
~

~
~
~
~


2  E2  E2
Ex
y
0
^
^
E   x  j y  E0
~

~
~

Polarização circular (esquerda)
^
^
E   x  j y  E0
~

~
~

Polarização circular (direita)
__
__
PROE CFI Aula4 090306
Polarização elíptica
__
^
^
~
~
~
E  x A j y B
^
^
^
^
~
~
~
~
E o, t   x A cos t  y sin t  E x x  E y y
~
E x2
A2

E y2
B2
1
Onda polarizada elipticamente
•
A polarização fica completamente especificada pela orientação e pela razão entre
os eixos da elipse, e pelo sentido segundo o qual a ponta do vector campo
eléctrico se move na elipse.
PROE CFI Aula4 090306
Polarização de ondas electromagnéticas
PROE CFI Aula4 090306
Polarização circular
  tg 1
E10 = E20 = E0
_
^
^
~
~
~
E ( z )  ( x  j y ) E0e  jkz
_
^
^
~
~
~
E ( z )  ( x  j y ) E0e  jkz
E2 (0, t )
 t
E1 (0, t )

Onda com polarização circular direita

Onda com polarização circular esquerda
Polarização linear
E1(z) e E2(z)
em quadratura no espaço e em fase no tempo
^
^
~
~
E (0, t )  ( x  y ) E0 cos t
~
(valor instantâneo)
PROE CFI Aula4 090306
• Difusão AM: polarização vertical
• TV: polarização horizontal
• Telemóveis: polarização circular direita
PROE CFI Aula4 090306
Condições fronteiras
•
Na prática os meios são limitados e o estudo da fenomenologia electromagnética envolve as
condições nas fronteiras.
•
As c.n.f.:
o dizem-nos quais as relações que têm que ser satisfeitas pelos campos nos 2 meios num
ponto qualquer da superfície interface.
o têm que ser respeitadas em qualquer ponto da interface e em qualquer instante de tempo.
o determinam-se aplicando as eqs. de Maxwell na forma integral a uma pequena região na
interface dos 2 meios.
PROE CFI Aula4 090306
 Div
E produzida pela carga eléctrica.
~
 Lei de Gauss
Fluxo total de
D   0 E que sai dum volume V limitado pela superficie S é igual à
~
~
carga eléctrica total contida no interior desse volume.
 D . ds
Sf
•
~
~

q
V
dv
Teorema da divergência do cálculo vectorial (Teorema de Gauss)
Fluxo de um campo vectorial U que sai de uma superficie fechada Sf é igual ao integral no
^
volume V da divergência de U.
n
~
Sf = S1 + S 2 + Sl

Sf

D . ds 
~
V
~
S1
 . D dv
~
^
Sl
n
~
~
 D
S2
~
PROE CFI Aula4 090306
^
n
~
^
Componentes normais à fronteira
n
~1
 D . ds  
Sf
~
~
V
S1
 dv
1
2
 B . ds  o
Sf
~
S3
h
S2
~
^
n
~2
As componentes normais da indução magnética numa superfície fronteira e ao atravessar a
superficie de separação dos 2 meios são contínuas.
^

n. B  B
~
~ 1
~ 2
 o
As componentes normais de ao atravessar a superfície de separação de 2 meios são descontínuas,
diferindo do valor da densidade de carga superficial.
^

n. D  D
~
~ 1
~ 2
 
s
PROE CFI Aula4 090306
Componentes tangenciais à fronteira
l

f
E . dl  
~
~

A
B
~
t
. dA
~
h1
1
h2
2
f
A componente tangencial do campo eléctrico através da interface entre os 2 meios é contínua.
^

n E  E
~
~1
~ 2
 o
A componente tangencial do campo magnético ao atravessar uma interface entre 2 meios é
descontínua, no caso de haver uma densidade de corrente superficial (película de corrente de
espessura infinitesimal), sendo a diferença dada pelo valor de Js.
^

n H  H
~
~ 1
~ 2
 J
~s
PROE CFI Aula4 090306
Fronteira dieléctrico/condutor perfeito
 Um meio com condutividade eléctrica perfeita: condutor eléctrico perfeito impede a
existência de quaisquer campos electromagnéticos no seu interior.
 O campo eléctrico é ortogonal á superfície condutora perfeita.
 A indução magnética é tangencial á superfície condutora perfeita.
• H eE
sobre a superfície condutora suportam-se respectivamente, na densidade
~
~
linear de corrente (ortogonal ao campo magnético tangencial) e na densidade de carga
superficial.
E
~
^
x
H
n
~
~
J
~s
PROE CFI Aula4 090306
σ=∞