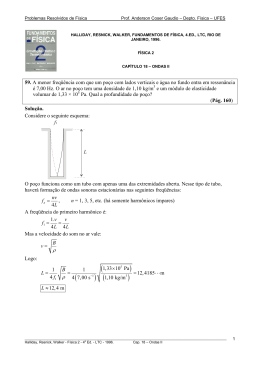
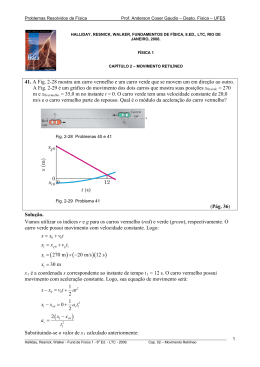
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
HALLIDAY, RESNICK, WALKER, FUNDAMENTOS DE FÍSICA, 4.ED., LTC, RIO DE
JANEIRO, 1996.
FÍSICA 2
CAPÍTULO 17 – ONDAS I
16. Uma onda de freqüência 500 Hz tem uma velocidade de 350 m/s. (a) Quão afastados estão dois
pontos que têm uma diferença de fase de π/3 rad? (b) Qual é a diferença de fase entre dois
deslocamentos, num determinado ponto, em tempos separados de 1,00 ms?
(Pág. 131)
Solução.
Seja y(x,t) uma onda transversal que progride no sentido positivo de x:
=
y( x ,t ) ym sen ( kx − ωt + φ )
Sendo conhecidas a freqüência f e a velocidade de propagação v, podemos determinar k e ω, que
serão usados adiante.
ω = 2π f
2π f
(1)
=
v
v
(a) Deseja-se determinar a distância, sobre o eixo x, que corresponda a uma diferença de fase φ =
π/3. Considere o seguinte esquema:
y
λ (2π)
k
=
ω
x
x (π/3)
Há pelo menos duas maneiras de calcular x. A primeira é por comparação:
λ
x
=
2π π / 3
λ
x=
6
Como:
2π
2π
v
λ =
=
=
2π f
k
f
v
Na equação acima, k foi substituído por (1):
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Física 2 - 4a Ed. - LTC - 1996.
Cap. 17 – Ondas I
1
Problemas Resolvidos de Física
=
x
Prof. Anderson Coser Gaudio – Depto. Física – UFES
( 350 m/s=
) 0,1166 m
v
=
6 f 6 ( 500 Hz )
x ≈ 0,117 m
A segunda forma de calcular x é considerando-se a existência de duas ondas, y1 e y2, defasadas de
π/3:
=
y1( x ,t ) ym sen ( kx − ωt )
π

=
y2( x ,t ) ym sen  kx − ωt − 
3

As funções y1 e y2 estão representadas no gráfico abaixo:
y
y1
y2
x2
x1
x
x
Como os pontos x1 e x2 correspondem a y1 = 0 e y2 = 0, respectivamente, temos:
y=
y=
0
1
2
π

ym sen ( kx=
ym sen  kx2 − ωt − 
1 − ωt )
3

kx1 − ωt = kx2 − ωt −
π
3
π
k ( x2 − x1 ) =
3
x2 − x1 = x =
π
3k
Utilizando-se (1):
x2 − x1 = x =
3
x=
π
2π f
v
v
6f
(b) Vamos utilizar o primeiro método usado no item (a) para o cálculo de ∆φ.
T
∆t
=
2π ∆φ
1
∆t
f
=
2π ∆φ
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Física 2 - 4a Ed. - LTC - 1996.
Cap. 17 – Ondas I
2
Problemas Resolvidos de Física
(
Prof. Anderson Coser Gaudio – Depto. Física – UFES
)(
)
∆=
φ 2π f ∆=
t 2π 500 s −1 1, 00 ×10−3 s= π rad
∆φ ≈ 3,14 rad
________________________________________________________________________________________________________
Halliday, Resnick, Walker - Física 2 - 4a Ed. - LTC - 1996.
Cap. 17 – Ondas I
3