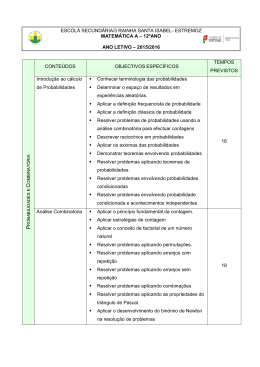
AGRUPAMENTO DE ESCOLAS DR. VIEIRA DE CARVALHO
Escola Básica e Secundária Dr. Vieira de Carvalho
Departamento de Matemática e Ciências Experimentais
Planificação Anual de Matemática A – 12º ano
Ano Letivo 2015/2016
TEMA
TÓPICOS
OBJETIVOS ESPECÍFICOS

AVALIAÇÃO*
Identificar e dar exemplos de experiências aleatórias e
de experiências deterministas.
PROBABILIDADES
 Conceitos
probabilísticos.
E
COMBINATÓRIA

Identificar e determinar todos os resultados possíveis
quando se realiza uma experiência aleatória.

Identificar e dar exemplos de acontecimentos de um
dado espaço de resultados.

Operações com
acontecimentos.

Identificar, definir e dar exemplos de acontecimentos
complementares, interseção de dois acontecimentos,
reunião de dois acontecimentos e acontecimentos
disjuntos.

Conhecer e aplicar as Leis de De Morgan.
 Observação
direta do aluno
na aula em
termos de
atitudes e de
trabalho
 Definição
frequencista de
probabilidade.

Calcular a probabilidade de acontecimentos de
uma experiência aleatória, aplicando:
PROBABILIDADES
- a definição frequencista de probabilidade –
E
Lei dos Grandes Números
COMBINATÓRIA
- a definição clássica de probabilidade –
 Definição clássica
de probabilidade.
Lei de Laplace
 Postura na sala
de aula e
interesse
demonstrado
pelas atividades
realizadas

Calcular a probabilidade de acontecimentos de
uma experiência aleatória, aplicando:
- a definição axiomática de probabilidade
PROBABILIDADES
E
COMBINATÓRIA.
 Definição
axiomática de
probabilidade.

Aplicar os axiomas da probabilidade.

Demonstrar propriedades de probabilidade.
 Fichas de
verificação de
conhecimentos :
- Avaliações
escritas.

Resolver problemas aplicando as propriedades da
probabilidade.

Definir probabilidade condicional.

Resolver problemas envolvendo probabilidade
condicional.

Obter probabilidade da interseção de acontecimentos
à custa da probabilidade condicional.
PROBABILIDADES
E
COMBINATÓRIA
 Probabilidade
condicional e
independência

Definir acontecimentos independentes.

Resolver problemas envolvendo acontecimentos
independentes.

Resolver problemas envolvendo probabilidade
condicional e acontecimentos independentes.
 Realização do
trabalho extra
proposto pelo
professor como
complemento
às atividades
realizadas em
sala de aula.

Definir através de uma tabela ou de um gráfico, a
distribuição de probabilidade de uma variável
aleatória.
PROBABILIDADES
E
COMBINATÓRIA.
 Distribuição de
frequências
relativas e
distribuição
de
probabilidade

Relacionar distribuição de frequências com
distribuição de probabilidade.

Relacionar média e desvio – padrão com valor médio
e desvio – padrão populacional.

Determinar o valor médio e o desvio – padrão de uma
distribuição de probabilidade.
 Perseverança
para ultrapassar
as dificuldades.

 Análise
combinatória.
Conhecer a aplicar o Principio Fundamental da
Contagem.

Aplicar estratégias de contagem.

Aplicar o conceito de fatorial de um número natural.

Resolver problemas aplicando:
- permutações.
- arranjos sem repetição.
- arranjos com repetição.
PROBABILIDADES
E
COMBINATÓRIA.
- combinações sem repetição.
 Triângulo de
Pascal.

triângulo de Pascal.

 Binómio de
Newton
Resolver problemas aplicando as propriedades do
Aplicar o desenvolvimento do binómio de Newton na
resolução de problemas.
Aplicar o cálculo combinatório na resolução de
problemas de probabilidade.
 Estudo
individual para
consolidação
dos
conhecimentos
 Modelo normal.

Identificar a Distribuição Normal.

Conhecer as características da Distribuição Normal.

Usar a calculadora gráfica para determinar
probabilidades referentes a uma variável aleatória
com Distribuição Normal.
PROBABILIDADES
E
COMBINATÓRIA.
 Histograma
versus função
densidade.
 Modelo
binomial.
 Empenho nas
atividades
escolares .

Identificar a Distribuição Binomial.

Resolver problemas envolvendo Distribuição Normal e
Distribuição Binomial.

Função
exponencial de
base superior a 1.

Identificar funções Exponenciais.

Conhecer as propriedades das funções exponenciais.

Resolver equações e inequações exponenciais.

Aplicar as transformações dos gráficos de funções a
funções exponenciais.

A plicar as funções exponenciais na modelação de
situações reais.

Aplicar a função exponencial de base e na modelação de
situações reais.
INTRODUÇÃO
AO CÁLCULO
DIFERENCIAL II

Função
logarítmica de
base superior a 1.

Identificar funções Logarítmicas.

Aplicar as transformações dos gráficos de funções a
funções logarítmicas.

Aplicar as propriedades operatórias dos logaritmos.

Resolver equações exponenciais e logarítmicas.

Resolver inequações com exponenciais e logaritmos.

Definir a função inversa de uma função exponencial ou
logarítmica.

Resolver problemas em contexto real usando funções
exponenciais e funções logarítmicas.

Organização e
rigor científico
com que
apresenta os
cadernos diários
e a resolução de
fichas de
trabalho
propostas.
 Teoria dos limites:
- Limite de uma
função segundo
Heine.
INTRODUÇÃO
AO CÁLCULO
DIFERENCIAL II
- Propriedades
operatórias sobre
limites.
- Indeterminações.

Calcular limites das funções por concretização da variável
independente.

Calcular limites laterais.

Aplicar a definição de limite segundo Heine.

Aplicar teoremas sobre limites no cálculo de limites.

Calcular limites quando 𝑥 → ± ∞ .

Levantar Indeterminações.

Calcular limites envolvendo funções exponenciais e
logarítmicas.
- Alguns limites
notáveis.

Calcular limites de sucessões.
 Participação na
aula.
 Continuidade.
Teorema de
Bolzano Cauchy.

Estudar a continuidade de uma função num ponto.

Estudar a continuidade lateral de uma função num
ponto.
INTRODUÇÃO
AO CÁLCULO
DIFERENCIAL II

Estudar a continuidade de uma função num intervalo.

Aplicar teoremas e propriedades sobre funções
contínuas.
 Assimptotas do
gráfico de uma
função

A plicar o Teorema de Bolzano – Cauchy.

Determinar as assimptotas do gráfico de uma função.

Resolver problemas usando continuidade.

Resolver problemas aplicando o conceito de assimptota
do gráfico de uma função.

Curiosidade
científica.






Derivadas.
INTRODUÇÃO AO
CÁLCULO
DIFERENCIAL II








Aplicações das
derivadas.






Definir derivada de uma função num ponto.
Interpretar geometricamente o valor da derivada de uma
função num ponto.
Determinar as derivadas laterais de ma função num ponto.
Interpretar derivadas infinitas.
Relacionar os conceitos de derivabilidade e de continuidade
de uma função num ponto.
Conhecer o significado de função derivada de uma função.
Demonstrar algumas regras de derivação.
Aplicar regras de derivação.
Derivar funções exponenciais e logarítmicas.
Calcular a segunda derivada de uma função.
Relacionar os gráficos de uma função e da respetiva função
derivada.
Relacionar os gráficos de uma função e da respetiva função
segunda derivada.
Determinar os extremos de uma função aplicando o
conceito de derivada.
Estudar a monotonia de uma função usando o conceito de
derivada.
Estudar o sentido das concavidades do gráfico de uma
função usando a segunda derivada da função.
Estudar analiticamente uma função (a calculadora é usada
apenas para confirmação dos resultados).
Escrever o modelo matemático correspondente a uma
situação real.
Resolver problemas de otimização.
 Trabalho fora do
contexto da sala
de aula.
 Revisões sobre
trigonometria.
TRIGONOMETRIA
E
NÚMEROS
COMPLEXOS

Conhecer e aplicar
trigonométricas.

Resolver equações trigonométricas.

Deduzir e aplicar as fórmulas trigonométricas do seno,
cosseno e tangente da soma e da diferença de dois ângulos.
 Funções
trigonométricas.
 Fórmulas
trigonométricas
do seno, cosseno
e tangente da
soma de dois
ângulos.
 Estudo das
funções
trigonométricas.
as
propriedades
das
funções
 Observação
direta do aluno
na aula em
termos de
atitudes e de
trabalho
Conhecer que 𝐥𝐢𝐦

Calcular limites aplicando o conhecimento de que
𝒙→𝟎
 Estudo intuitivo
𝒔𝒊𝒏 𝒙
do 𝐥𝐢𝐦
.
𝒙→𝟎
𝒙
𝐥𝐢𝐦
𝒙→𝟎
TRIGONOMETRIA
E
NÚMEROS
COMPLEXOS
𝒔𝒊𝒏 𝒙

𝒔𝒊𝒏 𝒙
𝒙
𝒙
=1
=1
 Limites com
funções
trigonométricas
 Postura na sala
de aula e
interesse
demonstrado
pelas atividades
realizadas
 Limites notáveis
 Derivada das
funções
trigonométricas.

Deduzir e aplicar as fórmulas das derivadas das funções
seno, cosseno e tangente.
 Números
complexos
TRIGONOMETRIA
E
NÚMEROS
COMPLEXOS

Identificar √−1 como

Conhecer o conjunto ℂ.

Representar geometricamente um número complexo.

Escrever números complexos na forma algébrica e na forma
trigonométrica.

Adicionar, subtrair,
complexos.
 Números
complexos na
forma algébrica.
 Representação
trigonométrica
de um número
complexo.
i ou seja a unidade imaginária.
multiplicar
e
dividir
 Fichas de
verificação de
conhecimentos :
números

Calcular potências de um número complexo.

Determinar raízes complexas de uma equação.

Calcular as raízes de índice n de um número complexo
escrito na forma trigonométrica.
- Avaliações
escritas.
TRIGONOMETRIA
E
NÚMEROS
COMPLEXOS
 Domínios
planos e
condições em
variável
complexa.

Representar no plano complexo conjuntos definidos por
condições.

Escrever uma condição que represente um conjunto de
pontos, definido no plano complexo.

Interpretar geometricamente condições em
como:
- |𝑍 − 𝑍1 | = 𝑟
- |𝑍 − 𝑍1 | = |𝑍 − 𝑍2 |
- 𝐼𝑚 ( 𝑍 − 𝑍1 ) = 𝑎
- 𝑅𝑒 ( 𝑍 − 𝑍1 ) = 𝑏
ℂ ,
tais
 Realização do
trabalho extra
proposto pelo
professor como
complemento
às atividades
realizadas em
sala de aula.
- 𝑎𝑟𝑔 ( 𝑍 − 𝑍1 ) = ∝
*Os instrumentos de avaliação referidos são comuns a todos os temas sendo, portanto, utilizados sempre ao longo do ano , sempre que o professor os considere
adequados.
OBJETIVOS TRANSVERSAIS

Selecionar estratégias de resolução de problemas.

Analisar situações da vida real identificando modelos matemáticos que permitam a sua interpretação e resolução.

Interpretar e criticar resultados no contexto do problema.

Resolver problemas nos domínios da Matemática.

Descobrir relações entre conceitos de Matemática.

Comunicar conceitos, raciocínios e ideias, oralmente e por escrito, com clareza e progressivo rigor lógico.

Usar corretamente o vocabulário e a simbologia específicos da Matemática.

Apresentar os textos de forma clara e organizada.

Discutir resultados, processos e ideias matemáticos.
• Identificar os dados, as condições e o objetivo do problema.
• Conhecer e pôr em prática estratégias de resolução de problemas, verificando a adequação de resultados obtidos e dos processos utilizados.
• Averiguar a possibilidade de abordagens diversificadas para a resolução de um problema
 Formular hipóteses e prever resultados.
 Resolver problemas nos domínios da Matemática, da Física, da Economia, das Ciências Humanas, ...
 Descobrir relações entre conceitos de Matemática.
 Formular generalizações a partir de experiências.
 Comunicar conceitos, raciocínios e ideias, oralmente e por escrito, com clareza e progressivo rigor lógico.
 Interpretar textos de Matemática.