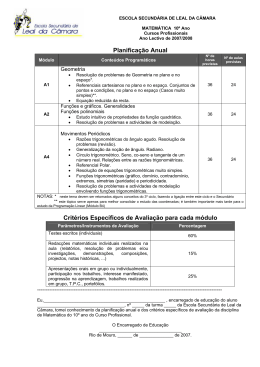
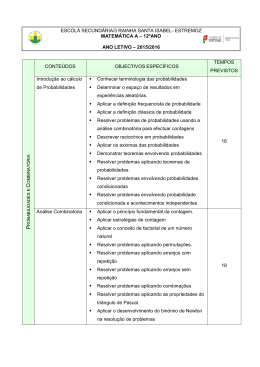
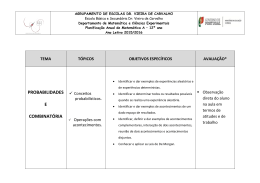
Agrupamento de Escolas de Torre de
Moncorvo
Planificação a longo prazo - Matemática 12o ano
2013/2014
PLANIFICAÇÃO A LONGO PRAZO
MATEMÁTICA
12º ANO
2013/2014
TEMA I: Probabilidades e Combinatória
CONTEÙDOS
Introdução ao Cálculo de Probabilidades:
• Experiência aleatória; conjunto de resultados; acontecimentos.
• Operações sobre acontecimentos.
• Aproximações conceptuais para probabilidade:
- aproximação frequencista de probabilidade;
- definição clássica de probabilidade ou de Laplace;
- definição axiomática de probabilidade; propriedades da probabilidade.
• Probabilidade condicionada; probabilidade da intersecção de acontecimentos.
Acontecimentos independentes.
•
•
•
•
•
•
OBJECTIVOS
30 aulas de 90 minutos
Determinar o espaço amostral de uma experiência aleatória.
Calcular a probabilidade de um acontecimento.
Verificar as propriedades da axiomática aplicada aos vários conceitos
de probabilidade.
Aplicar as propriedades das operações com acontecimentos.
Resolver problemas.
Explicar raciocínios, usando a linguagem específica das
probabilidades.
Distribuição de frequências relativas e distribuição de probabilidades:
• Variável aleatória; função massa de probabilidade:
- distribuição de probabilidades de uma variável aleatória discreta.
• Modelo binomial
• Modelo normal; histograma versus função densidade.
•
•
•
•
•
Definir variável aleatória.
Definir a função massa de probabilidade.
Identificar uma distribuição normal.
Conhecer as características de uma distribuição normal..
Resolver problemas que envolvam os conceitos referidos.
Análise combinatória:
• Arranjos completos, arranjos simples, permutações e combinações.
• Triângulo de Pascal.
• Binómio de Newton.
• Aplicação ao cálculo de probabilidades.
•
•
•
•
Aplicar o princípio fundamental da contagem.
Aplicar estratégias de contagem.
Aplicar o conceito de factorial de um número natural.
Resolver problemas aplicando:
- permutações;
- arranjos;
- combinações.
Resolver problemas aplicando as propriedades do Triângulo de Pascal.
Aplicar o desenvolvimento do binómio de Newton na resolução de
problemas.
•
•
TEMA II: Introdução ao Cálculo Diferencial II
CONTEÙDOS
Funções exponenciais e logarítmicas:
• Função exponencial de base superior a um; estudo das propriedades
analíticas e gráficas.
• Função logarítmica de base superior a um; estudo das propriedades analíticas
e gráficas.
• Regras operatórias de exponenciais e logaritmos.
• Utilização de funções exponenciais e logarítmicas na modelação de situações
reais.
Teoria de limites:
• Limite de função segundo Heine.
• Propriedades operatórias sobre limites.
• Limites notáveis.
• Indeterminações.
• Assimptotas.
• Continuidade.
• Teorema de Bolzano-Cauchy e aplicações numéricas.
Cálculo Diferencial:
• Funções deriváveis. Regras de derivação.
• Segundas derivadas e concavidade.
• Estudo de funções.
• Problemas de optimização.
OBJECTIVOS
•
24 aulas de 90 minutos
•
•
•
•
•
Interpretar gráfica e analiticamente as propriedades das funções exponencial e
logarítmica.
Aplicar as regras operatórias sobre exponenciais e logaritmos.
Resolver equações e inequações com exponenciais e logaritmos.
Definir a função inversa de uma função exponencial ou logarítmica.
Resolver problemas envolvendo funções exponenciais e logarítmicas.
Interpretar fenómenos descritos por funções exponenciais e logarítmicas.
•
•
•
•
•
•
•
Calcular limites de funções.
Usar as regras operatórias sobre limites.
Levantar indeterminações.
Determinar assimptotas.
Estudar a continuidade de uma função.
Aplicar o teorema de Bolzano-Cauchy ao estudo de funções.
Calcular limites de sucessões.
•
•
•
Definir derivada de uma função num ponto.
Interpretar geometricamente o valor da derivada de uma função num ponto.
Interpretar a derivada como velocidade ou aceleração de um móvel num
ponto.
Calcular derivadas.
Estudar funções usando derivadas.
Resolver problemas usando funções.
•
•
•
TEMA III: Trigonometria e Números Complexos
24 aulas de 90 minutos
CONTEÙDOS
Funções seno, co-seno, tangente:
• Funções trigonométricas como funções reais de variável real.
• Estudo intuitivo das funções trigonométricas.
• Equações trigonométricas.
• Fórmulas trigonométricas da soma e da diferença de dois ângulos.
• Limites de funções trigonométricas.
• Derivada das funções trigonométricas.
• Utilização de funções trigonométricas na modelação de situações reais.
Complexos:
• Evolução do conceito de número.
• Números complexos. O número i. O conjunto dos números complexos.
• A forma algébrica dos complexos. Operações com complexos na forma algébrica.
• Representação de complexos na forma trigonométrica. Escrita de complexos nas duas formas,
passando de uma para outra. Operações com complexos na forma trigonométrica.
Interpretações geométricas das operações.
• Domínios planos e condições em variável complexa.
OBJECTIVOS
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Indicar características de funções trigonométricas (sinal,
zeros, monotonia, paridade, período, continuidade,
extremos, gráfico, …)
Resolver equações trigonométricas.
Calcular limites de funções trigonométricas.
Derivar funções trigonométricas.
Resolver problemas usando funções trigonométricas.
Operar com números complexos na forma algébrica.
Calcular raízes quadradas de um real negativo.
Converter a forma algébrica na trigonométrica e vice-versa.
Operar com complexos na forma trigonométrica.
Calcular as raízes de índice n de um número complexo
escrito na forma trigonométrica.
Representar geometricamente as n raízes de índice n de um
complexo.
Determinar as raízes complexas de uma equação.
Representar no plano complexo conjuntos definidos por
condições.
Escrever uma condição que represente um conjunto de
pontos, definido no plano complexo.