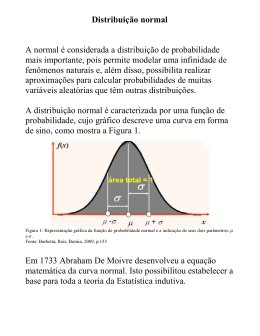
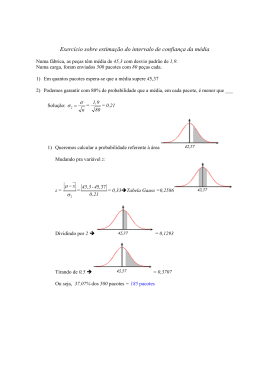
A fórmula de Gauss
Bruno Carvalho Palvarini
Quando cursava o mestrado em Engenharia ouvi de um professor a fantástica
resolução de um problema complexo pelo matemático Gauss quando este tinha
apenas oito anos de idade. Tenho usado a passagem como um bom exemplo de
resolução de situações de alta complexidade e de outras características fundamentais
para a gestão de processos. Aproveito, aqui, para fazer uma pequena adaptação da
história, partindo da formulação real que deveria ser solucionada antes que a classe
pudesse ser dispensada:
- Qual o valor da soma dos primeiros 1.000 números naturais? Em outras
palavras: tomando-se o conjunto A = {1, 2, 3, 4, ..., 999, 1.000}, qual o resultado
da soma de todos os seus elementos?
Segundo o relato, o professor propusera o problema certo de que com tal atitude teria
descanso, pelo menos, até o fim do dia; no entanto, cinco minutos após lançado o
desafio, eis que Gauss lhe traz a resposta à questão e, diante da dúvida do mestre,
demonstra a forma utilizada em sua resolução, tão revolucionária que fez o professor
identificar ali o surgimento de uma fantástica vocação matemática.
Imaginemos agora que três alunos, dentre eles Gauss, estivessem a resolver o
problema nos dias atuais. Além disso, imaginemos que o professor, na ânsia de tornar
a resolução mais difícil, tivesse dado apenas dois minutos para que a solução fosse
entregue.
Desesperado, o primeiro aluno pôs-se a somar a sequência a partir de seu início,
tomando seus números aos pares e, a partir dos resultados parciais, efetuando uma
nova soma (por exemplo: 1+2=3; 3+3=6; 6+4=10, e assim sucessivamente). Ao fim do
tempo previsto, com grande esforço e concentração, digamos que o menino houvesse
efetuado 29 operações de soma – relativas aos trinta primeiros números da sequência
–, chegando a um valor igual a 465 (um erro de cerca de 99,91% em relação ao valor
correto, 500.500). Note-se que, caso tivesse conseguido completar a resolução
segundo o método escolhido, seriam necessárias 999 operações matemáticas, com
somas parciais crescentes, o que aumentaria excessivamente o risco de erros e
demandaria um tempo não disponível.
O segundo aluno, refletindo os primeiros vinte segundos quanto à dificuldade de
alcançar o resultado correto, decidira partir para uma variação do primeiro método –
como os últimos números da sequência representavam os valores mais altos do
conjunto, sua soma deveria ser mais representativa que a dos primeiros. Então,
partindo do pressuposto que seria impossível entregar a solução correta no prazo
previsto, começou a somar os elementos do fim para o começo (ou seja,
1.000+999=1.999; 1.999+998=2.997 e assim sucessivamente). Ao fim dos dois
minutos, sendo mais ágil que o primeiro aluno, conseguiu também realizar a soma de
trinta números, chegando ao valor 29.565. De novo, verificamos que, apesar da
engenhosidade do menino em identificar os pesos dos elementos e em reduzir o
número de operações algébricas (29, uma vez que não tencionava realizar todas as
somas), o erro associado ainda mostrou-se absurdamente alto, de cerca de 94,10%
em relação ao resultado correto. Tal método é similar ao que atualmente costumamos
chamar corriqueiramente de “princípio de Pareto”, ao estimarmos que alguns
elementos concentram a maior parte da informação necessária – mas o próprio Pareto
não chegou exatamente a tais conclusões para todo e qualquer sistema. Isso, no
entanto, seria objeto de um outro texto...
O terceiro aluno, Gauss, gastou o primeiro minuto de seu tempo para avaliar o
problema; como o primeiro colega, verificou a complexidade de realizar 999 operações
em apenas dois minutos e resolveu descartar tal método. A exemplo do segundo
1
menino, concluiu que os números de menor valor concentravam-se no início da
sequência e os maiores, em seu fim, mas brincando com o conjunto-problema,
descobriu um fato interessante: a soma de elementos em posições relativas
semelhantes era idêntica. Em outras palavras, a soma dos extremos da sequência
(1+1.000=1.001) possuía o mesmo valor que a soma do par seguinte (2+999=1.001) e
assim, sucessivamente. Dessa forma, existindo uma quantidade de pares de tais
elementos igual à metade do número de elementos no conjunto (500 pares), bastaria
realizar três operações algébricas – uma soma, por exemplo entre o primeiro e o
último número –, uma divisão – a metade da quantidade de elementos – e uma
multiplicação entre as duas parcelas anteriores, para se chegar ao resultado exato do
problema! Ao fim dos dois minutos, Gauss tinha 100% de correção em seu resultado,
cumprindo também a exigência do tempo e tendo minimizado o risco de tal forma que,
com a aplicação de seu método, fora possível revisar e conferir as poucas operações
algébricas realizadas.
A realidade enfrentada pelos três alunos era idêntica – assim como a complexidade do
problema e a exiguidade de tempo e de recursos. A primeira forma de resolução
demonstrou o grave erro de falta de inovação e de planejamento. Partindo diretamente
para a operação, o garoto partiu também direto para o fracasso, uma vez que o
método se mostrara inaplicável ao contexto. Entretanto, havia um sentimento de
demonstrar esforço e trabalho duro (ainda que em vão), na esperança de conseguir
com isso o perdão do professor pelo resultado incorreto ou, ainda, a possibilidade de
transferência da responsabilidade para o próprio professor – equivocado no mau
dimensionamento dos recursos necessários para a resolução do problema (mais
tempo, mais equipes – para dividir as somas em grupos menores e paralelos de
números, por exemplo – ou calculadoras e computadores para realizar as operações
de forma mais rápida).
A segunda resolução demonstrou uma evolução em termos de planejamento mas um
crasso erro de avaliação, ao simplificar a realidade complexa; descolado da verdade
por não possuir dados que comprovassem suas suposições, o aluno presumiu que
poderia somar apenas os elementos mais relevantes da sequência frente aos recursos
disponíveis. Esperava, assim, que o problema fosse insolúvel e que sua estimativa
fosse aceita diante da incapacidade do professor também conhecer o valor final
esperado.
A solução de Gauss foi perfeita em todos os aspectos; na inovação decorrente da
reflexão voltada ao problema a ser entregue e não à operação (realização de um
número excessivo de somas trabalhosas), na minimização do risco associado (sempre
um número fixo de três operações algébricas, independente do tamanho da
sequência), no cumprimento das premissas de recursos disponíveis (uma única
pessoa, no tempo previsto, sem o uso de outros equipamentos) e, principalmente, no
respeito e na compreensão da complexidade da realidade. Problemas complexos
merecem ser assim reconhecidos, para que se busquem soluções simples. Eis a
principal diferença entre as três abordagens: a primeira partiu de uma realidade e de
uma resolução complexas e fracassou. A segunda, de uma premissa equivocada de
realidade simplificada e não houve como consertá-la durante a evolução dos
trabalhos. A terceira abordagem é admirável por considerar toda a complexidade do
problema, não promovendo qualquer simplificação em seu entendimento; porém,
apresenta uma brutal e definitiva simplicidade em sua resolução.
Em muitos casos, a vida de nossas organizações ainda compele pessoas e unidades
– por motivos culturais e pela repetição de antigas práticas –, a utilizar
preferencialmente a primeira abordagem ou, no máximo, a adotar a segunda
alternativa e considerá-la uma grande inovação.
Inovação, de verdade, encontramos nas ideias de Gauss.
2