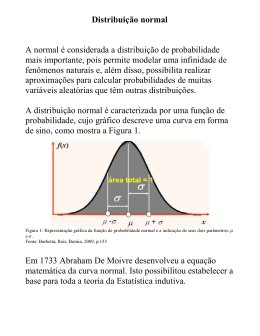
Integração Numérica – Grau de uma regra
Uma regra diz-se de grau n se integrar sem erro todos os polinómios de grau ≤n e existir
pelo menos um polinómio de grau n+1 que não é integrado exactamente.
Exemplos:
Regra do Trapézio (polinómio interpolador de grau 1)
f(x)
Pela modo como foi construída, a regra integra (pelo
menos) funções lineares.
Eh = −
1
⋅ (b − a)3 ⋅ f ''(ξ )
12
p(x)
Ih(f)
Da análise (da ordem da derivada) da expressão do
erro, constata-se que funções de grau 1 (logo com
segunda derivada nula) são integradas sem erro e que
funções de grau 2 (logo com segunda derivada não
nula) são integradas com erro, logo a regra do trapézio
tem grau 1
a
b
Matemática Computacional, MEMec, LEAN, MEAer
Integração Numérica – Grau de uma regra
Exemplos (cont.):
f(x)
Regra do ponto médio (polinómio interpolador de grau 0)
Pelo modo como foi construído, a regra integra (pelo
menos) funções constantes.
Eh =
1
⋅ (b − a)3 ⋅ f (2) (ξ )
24
Ih(f)
a
Contudo, da análise (da ordem da derivada) da
expressão do erro, constata-se que funções de grau 1
(logo com segunda derivada nula) são integradas sem
erro e que funções de grau 2 (logo com segunda
derivada não nula) são integradas com erro, logo a
regra do ponto médio tem grau 1
(a+b)/2
b
f(x)
Ih(f)
a
(a+b)/2
b
Matemática Computacional, MEMec, LEAN, MEAer
Integração Numérica – Grau de uma regra
Exemplos (cont.):
Regra de Simpson (polinómio interpolador de grau 2)
p(x)
Pelo modo como foi construído, a regra integra (pelo
menos) funções quadráticas.
Eh = −
1
⋅ (b − a)5 ⋅ f (4) (ξ )
2880
f(x)
Ih(f)
a
(a+b)/2
b
Contudo, da análise (da ordem da derivada) da
expressão do erro, constata-se que funções de grau 3
(logo com quarta derivada nula) são integradas sem
erro e que funções de grau 4 (logo com quarta
derivada não nula) são integradas com erro, logo a
regra do ponto médio tem grau 3
Matemática Computacional, MEMec, LEAN, MEAer
Integração Numérica – Regras de Gauss
Regras de integração de Newton-Cotes
b
I( f ) =

a
b
f (x)d (x) ≈


N
pn (x)d (x) =
Ai ⋅ f (xi ) =Ih ( f )
i =1
a
↑
nós de
interpolação
Em Newton-Cotes os nós de interpolação estão definidos “à partida” (nós equidistantes), o
que limita o grau de exactidão da regra de integração
Regras de integração de Gauss - Nas regras de Gauss a posição dos nós de interpolação é
escolhida “do melhor modo possível”

N
Ih ( f ) =
i =1
Ai ⋅ f (xi )



Os pesos Ai
e a localização xi
são parâmetros
a definir
Dispomos de 2N parâmetros (os valores dos pesos Ai e a localização dos pontos xi)
→ a regra terá grau 2N – 1
Matemática Computacional, MEMec, LEAN, MEAer
Regra de Gauss com 2 pontos
Exercício: a) Deduzir o valor dos pesos Ai e a localização das abcissas xi de modo à regra
seguinte ter o maior grau possível.
+1
I( f ) =

f (x)d (x) ≈ A1 ⋅ f (x1 ) + A2 ⋅ f (x2 ) = Ih ( f )
−1
b) Indicar o grau da regra.
Nota: Devido à linearidade do operador integral, se a regra integrar sem erro os monómios
1, x, x2, ..., xn, então integra sem erro todos os polinómios de grau ≤ n

pn (x) dx =





a0 + a1 x + a2 x 2 + ... + an x n dx = a0 1 dx + a1 x dx + a2 x 2 dx + ... + an x n dx
Resolução:


I( f ) = f (x)d (x)

−1


Ih ( f ) = A1 ⋅ f (x1 ) + A2 ⋅ f (x2 )
+1

Temos 4 incógnitas (A1, A2, x1, x2)
→ necessitamos de 4 equações
Matemática Computacional, MEMec, LEAN, MEAer
Regra de Gauss com 2 pontos
f (x) = 1 →

I( f ) = f (x) d (x) = 1 d (x) = x −1 = 2 

−1
−1

Ih ( f ) = A1 ⋅ f (x1 ) + A2 ⋅ f (x2 ) = A1 + A2 
f ( x) = x →


I( f ) = f ( x) d ( x) =
=0

−1

−1
−1

Ih ( f ) = A1 ⋅ f (x1 ) + A2 ⋅ f (x2 ) = A1 ⋅ x1 + A2 ⋅ x2 
f (x) = x 2 →


I( f ) = f ( x) d ( x) =


−1
−1

2
2
Ih ( f ) = A1 ⋅ f (x1 ) + A2 ⋅ f (x2 ) = A1 ⋅ (x1 ) + A2 ⋅ (x2 ) 
+1

+1

+1

+1

+1

+1

+1
x2
x d ( x) =
2
x3
2
x d ( x) =
3
 A1 + A2 = 2
+1
 A1 ⋅ x1 + A2 ⋅ x2 = 0
+1
2
=
3
−1
 A1 ⋅ (x1 )2 + A2 ⋅ (x2 )2 =
2
3
Matemática Computacional, MEMec, LEAN, MEAer
Regra de Gauss com 2 pontos


=0
I( f ) = f ( x) d ( x) =

−1

−1
−1

Ih ( f ) = A1 ⋅ f (x1 ) + A2 ⋅ f (x2 ) = A1 ⋅ (x1 )3 + A2 ⋅ (x2 )3 
+1
f (x) = x 3 →

+1

x4
3
x d ( x) =
4
+1
 A1 ⋅ (x1 )3 + A2 ⋅ (x2 )3 = 0
Resulta o sistema de 4 equações não lineares (a 4 incógnitas)
 A1 + A2 = 2

 A1 ⋅ x1 + A2 ⋅ x2 = 0


2
2
2
 A1 ⋅ (x1 ) + A2 ⋅ (x2 ) =
3


3
3
 A1 ⋅ (x1 ) + A2 ⋅ (x2 ) = 0
Ou seja,
Solução
Ih ( f ) = A1 ⋅ f (x1 ) + A2 ⋅ f (x2 ) 
 A1 = A2 = 1


1
−
=
=
x
x
 1 2
3

 1 
 1 
Ih ( f ) = 1 × f  −
1
f
+
×

+

3
3


Matemática Computacional, MEMec, LEAN, MEAer
Regra de Gauss com 2 pontos
Grau da regra de Gauss com 2 pontos
Pelo modo como foi construída, a regra tem (pelo menos) grau 3.
Terá grau 4?
+1
I( f ) =
f ( x) = x
4
→

−1
+1
f (x) d ( x) =

−1
x5
4
x d (x) =
5
+1
=
−1
2
5
4
4
 1 
 1   1   1  1 1 2
Ih ( f ) = 1 × f  −
1
f
+
×


 =−
 +
 =9+9=9
3
3
3
3



 
 

 I( f ) =
2 2
≠ = Ih ( f )
5 9
pelo que não tem grau 4, ou seja a regra
de Gauss com 2 pontos tem grau 3
→ as regras de Gauss com N pontos tem grau 2N – 1
Nota: a dedução das regras de Newton-Cotes poderiam ter sido efectuadas de modo
análogo à utilizada nesta dedução da regra de Gauss com 2 pontos
Matemática Computacional, MEMec, LEAN, MEAer
Comparação da regra do trapézio com regra de Gauss
Trapézio (2 pontos)
f(x)
Ih ( f ) =
b−a
⋅ [ f (a) + f (b)]
2
Ih(f)
Grau 1
a
b
Gauss com 2 pontos
Ih ( f ) = A1 ⋅ f (x1 ) + A2 ⋅ f (x2 )
f(x)
Grau 3
Ih(f)
a x1
Para [a, b] = [−1, +1]
x2 b
 1 
 1 
+
1
×
Ih ( f ) = 1 × f  −
f

+

3
3


Matemática Computacional, MEMec, LEAN, MEAer
Regras de Gauss-Legendre
b
I( f ) =


N
f (x) dx ≈
Ai ⋅ f (xi ) = Ih ( f )
i =1
a
Para Gauss-Legendre os pesos Ai e a localização dos pontos xi encontra-se tabelado para o
intervalo [a,b]=[–1,+1].
Para utilizarmos a informação das tabelas é necessário efectuar uma mudança de variável
para o intervalo [–1,+1],
+1
b
I( f ) =
+1
 f (x) dx =  f ( x(ξ )) ⋅ J(ξ ) dξ =  F(ξ ) dξ ≈  A ⋅ F(ξ ) = I ( f )
−1
a
II
dx
dξ

N
i
i
h
i =1
−1
F (ξ )
Mudança de variável para o intervalo [–1,+1]
-1
+1
ξ
a
b
x
x(ξ ) = a ×
1−ξ
1+ξ
+ b×
2
2
,
J=
dx b − a
=
dξ
2
Matemática Computacional, MEMec, LEAN, MEAer
Regras de Gauss-Legendre no intervalo [-1,+1]
+1

I( f ) = F (ξ ) dξ
Nº de pontos, N
Abcissas ξi
Pesos Ai
1
0
2
−1
 A ⋅ F(ξ )
N
Ih ( f ) =
i
±1
2
i
3
0
i =1
3
4
1
± 3/5
89
59
± (3 − 2 6 / 5) / 7
(18 + 30) 36
± (3 + 2 6 / 5) / 7
(18 − 30) 36
O erro associado às formulas de Gauss-Legendre (com N pontos) é,
2 N +1
Eh = C N × (b − a)
×f
(2 N )
(η ) ,
(N !)4
CN =
,
3
(2N + 1) × ((2N)!)
η ∈[a , b]
Matemática Computacional, MEMec, LEAN, MEAer