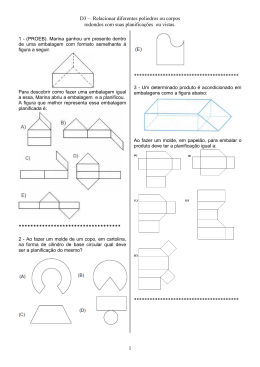
Treino Matemática – Planificação de Sólidos e Trigonometria Básica
1.Observe o prisma hexagonal regular ilustrado a
seguir:
Dentre as alternativas a seguir, a que representa
uma planificação para esse sólido é
3.Ao fazer um molde de um copo, em cartolina,
na forma de cilindro de base circular qual deve
ser a planificação do mesmo?
(Resp. D)
(Resp:c)
2.Marina ganhou um presente dentro de uma
embalagem com formato semelhante á figura a
seguir.
4. Um determinado produto é acondicionado em
embalagens como a figura abaixo:
Para descobrir como fazer uma embalagem igual
a essa, Marina abriu a embalagem e a planificou.
A figura que melhor representa essa embalagem
planificada é: resp. E
Ao fazer um molde, em papelão, para embalar o
produto deve ter a planificação igual a: resp. A
1
Treino Matemática – Planificação de Sólidos e Trigonometria Básica
6.A figura abaixo representa a planificação de um
sólido geométrico.
O sólido planificado é:
(A) uma pirâmide de base hexagonal.
(B) um prisma de base hexagonal.
(C) um paralelepípedo.
(D) um hexaedro.
(E) um prisma de base pentagonal.
5. O formato dos doces de uma determinada
fábrica tem o formato de um tronco de cone.
Como indicado na figura abaixo:
7.Considere as figuras abaixo:
Ao fazer um molde, em papel, para embalar os
produtos deve ter a planificação igual a:
RESPOSTA: A
As figuras I, II e III correspondem,
respectivamente, às planificações de:
A) prisma, cilindro, cone.
B) pirâmide, cone, cilindro.
C) prisma, pirâmide, cone.
D) pirâmide, prisma, cone.
E) pirâmide, cone, prisma.
8.A figura abaixo representa a planificação de um
sólido geométrico.
Qual é esse sólido?
2
Treino Matemática – Planificação de Sólidos e Trigonometria Básica
A) Pirâmide de base hexagonal
B) Pirâmide de base triangular
C) Prisma de base hexagonal
D) Prisma de base triangular
E) Prisma de base quadrangular.
9.Uma determinada caixa de presentes tem a
forma de um tetraedro regular, que nada mais é
que uma pirâmide em que todas as faces são
triângulos equiláteros. Esta caixa, desmontada,
corresponde à planificação descrita em
Sabendo que tg (60 º )  3 , a distância total, em
km, que Pedro percorre no seu trajeto de casa
para a escola é de:
3
4
(B) 4  3
(A) 4 
4 3
3
(D) 4 3
(E) 4  4 3
(C) 4 
12.Para consertar um telhado, o pedreiro Pedro
colocou uma escada de 8 metros de comprimento
numa parede, formando com ela um ângulo de
60º.
(resposta a)
10.Uma barraca de acampamento tem a forma de
uma pirâmide de base quandrangular e cada face
dela, inclusive a base, foi feita com uma lona de
cor diferente. Em cada vértice, foi colocado um
protetor de couro. Para fazer esta barraca foi
preciso dispor de
(A) 5 cortes de lona de cor diferente e 6
protetores de couro.
(B) 5 cortes de lona de cor diferente e 5
protetores de couro.
(C) 6 cortes de lona de cor diferente e 5
protetores de couro.
(D) 6 cortes de lona de cor diferente e 6
protetores de couro.
(E) 4 cortes de lona de cor diferente e 7
protetores de couro.
Sabendo
cos(60º ) 
que:
( sen (60 º ) 
3
, tg (60 º )  3
2
1
). A altura da parede que o pedreiro
2
apoiou a escada é:
(A) 5 m.
11.Para se deslocar de sua casa até a sua
escola, Pedro percorre o trajeto representado na
figura abaixo.
(B) 4 3 m
(C) 8 m.
(D) 8 3 m
(E) 4 m
13.Para permitir o acesso a um monumento que
está em um pedestal de 1,5 m de altura, será
3
Treino Matemática – Planificação de Sólidos e Trigonometria Básica
construída uma rampa com inclinação de 30º com
o solo, conforme a ilustração abaixo:
Sabendo
que:
( sen(30º ) 
distância de 100 m, e consegue obter um ângulo
de 55º.
A altura
do
edifício
aproximadamente:
(A) 58 m
(B) 83 m
(C) 115 m
(D) 144 m
(E) 175 m
3
1
, tg (30 º ) 
3
2
3
). A altura da parede que o
2
pedreiro apoiou a escada é:
4,5 3
(A)
m
3
(B) 3 m.
(C) 3 m
(D) 1,5  3 m.
(E) 4 m
cos(30 º ) 
é,
em
metros,
16. Para o abastecimento de água tratada de uma
pequena cidade, foi construído um reservatório
com a forma de um paralelepípedo retângulo,
conforme a representação abaixo.
14.Um caminhão sobe uma rampa inclinada 15º
em relação ao plano horizontal. Sabendo-se que
a distância HORIZONTAL que separa o início da
rampa até o ponto vertical mede 24 m, a que
altura, em metros, aproximadamente, estará o
caminhão depois de percorrer toda a rampa?
A capacidade máxima de água desse reservatório
é de
(A) 135 m³
(B) 180 m³
(C) 450 m³
(D) 550 m³
(E) 900 m³
17.Um copo cilíndrico, com 4 cm de raio e 12 cm
de altura, está com água até a altura de 8 cm.
Foram então colocadas em seu interior n bolas de
gude, e o nível da água atingiu a boca do copo,
sem derramamento.
3
Qual é o volume, em cm , de todas as n bolas de
gude juntas?
(A) 32π
(B) 48π
(C) 64π
(D) 80π
(E) 96π
(A) 6.
(B) 23.
(C) 25
(D) 92
(E) 100
15.O teodolito é um instrumento utilizado para
medir ângulos. Um engenheiro aponta um
teodolito contra o topo de um edifício, a uma
18. Para desenvolver a visão espacial dos
estudantes,
4
o
professor
ofereceu-lhes
uma
Treino Matemática – Planificação de Sólidos e Trigonometria Básica
planificação de uma pirâmide de base quadrada
como a figura:
Sabendo-se que o volume da pirâmide é de 6 m³,
então o volume do cubo, em m³, é igual a:
(A) 9
(B) 12
(C) 15
(D) 18
(E) 21
21.Uma embalagem de talco de forma cilíndrica
possui 15 centímetros de altura e base com 3
centímetros de raio. Qual é o volume máximo, em
cm³, de talco que essa embalagem comporta?
A) 540 π
B) 180 π
C) 135 π
D) 90 π
E) 45 π
A área da base dessa pirâmide é 100 cm² e a
área de cada face é 80 cm².
A área total, no caso da pirâmide considerada, é
igual a:
(A) 320 cm²
(B) 340 cm²
(C) 360 cm²
(D) 400 cm²
(E) 420 cm²
22.(ENEM 2005). Os três recipientes da figura
têm formas diferentes, mas a mesma altura e o
mesmo diâmetro da boca. Neles são colocados
líquido até a metade de sua altura, conforme
indicado nas figuras.
Representando por V1, V2 e V3 o volume de
líquido em cada um dos recipientes, tem-se
19.De um bloco cúbico de isopor de aresta 3a,
recorta-se o sólido, em forma de H, mostrado na
figura abaixo.
O volume do sólido é:
(A) 27a³.
(B) 21a³.
(C) 18a³.
(D) 14a³.
(E) 9a³.
(A) V1 = V2 = V3
(B) V1 < V3 < V2
(C) V1 = V3 < V2
(D) V3 < V1 < V2
(E) V1 < V2 = V3
20.Um empresário produz sólidos pedagógicos de
plástico, como por exemplo, pirâmides. Ele quer
embalá-las em caixas no formato de um cubo,
sabendo que a pirâmide está inscrita, como
mostra a figura abaixo.
23. Uma pirâmide é mergulhada num aquário
cúbico cheio d’água, como na figura.
O número mais próximo que expressa a relação
entre a quantidade de água final no aquário e a
inicial (antes de mergulhar a pirâmide) é de,
aproximadamente,
5
Treino Matemática – Planificação de Sólidos e Trigonometria Básica
(A) 25%
(B) 33%
(C) 50%
(D) 67%
(E) 72%
24.Observe o gráfico a seguir.
Qual a função que melhor representa esse gráfico
no intervalo [0, 2 ] ?
(A) y = – cos x.
 x
(B) y  cos 
2
(C) y  sen( x)
(D) y  sen 2 x
(E) 2senx .
25. Observe o gráfico a seguir.
Qual a função que melhor representa esse gráfico
no intervalo [2 , 2 ] ?
 x
(A) y  cos  .
2
(B) y  sen x 
(C) y  sen(2 x)
(D) y = – cos(x).
(E) y  2 cos(x)
26.O gráfico de função y  cos x é:
Resposta: B
27. Qual dos gráficos, abaixo, representa a
função y = 2 + senx? (Resp. D)
6
Treino Matemática – Planificação de Sólidos e Trigonometria Básica
A função que gerou este gráfico é representada
por
(A) y = 1 + cos(x)
(B) y = –1 + cos(x)
(C) y = 1 + sen(x)
(D) y = –1 + sen(x)
(E) y = 1 + tg(x)
28. Observe o seguinte esboço de um gráfico:
7