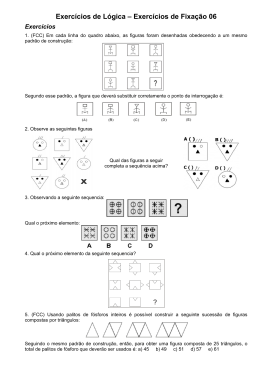
PLANO DE AULA
Dados de identificação
1-ESCOLA DE ENSINO MÉDIO MACÁRIO BORBA
Município: Sombrio, SC
Disciplina: Matemática
Série: 2º ano
Nível: Ensino Médio
Professora: Erodíades Daboit Possamai
Turma: 2
Tempo previsto: 4 h.a.
2-Tema: Sequências e Progressões
Subtemas: Sequências, Progressões Aritméticas e Progressões Geométricas.
3) Justificativa
O estudo das sequências e progressões são necessárias na resolução de diversas
situações do nosso cotidiano. Existem relatos que há muito tempo atrás os
egípcios e babilônicos utilizavam esse método na resolução de problemas. As
progressões aritméticas e geométricas estão bastante presentes no nosso
cotidiano e são necessárias para calcular as grandezas que sofrem variações
iguais em intervalos de tempos iguais, ou seja dentro de um padrão, como o
crescimento populacional, o crescimento de uma bactéria, dentre outras.
4) Objetivos:

Identificar padrões numéricos e sequências;

Diferenciar PA e PG;

Conceituar sequências P.A e P.G;

Interpretar e calcular os termos gerais da P.A. e P.G;

Calcular a soma dos termos de uma PA e de uma PG;

Resolver situações problemas que envolvam PA e PG.
5) Conteúdos envolvidos (conteúdos pré-requisitos para o desenvolvimento
da aula).
As operações básicas;
Função.
.
6) Estratégias:
6.1- recursos: disponível em sala de aula, televisão ou data show, lousa.
6.2- técnicas: Aula expositiva e dialogada, atividades em sala de aula.
7) Procedimentos:
7.1- Problematização:
Situação 1:Utilizando –se de uma folha de papel A4, representamos a PA e a PG
através do estágio de dobradura da folha. Vamos analisar vários aspectos, o
primeiro é a quantidade de partes da folha a cada dobradura que realizamos (PG),
a segunda é o tamanho da parte da folha em relação ao todo em cada etapa da
dobradura(PG) e a terceira é analisar o número de vezes que realizamos a dobra
(PA).
Situação 2: As empresas A e B foram inauguradas na mesma data. Nos
ultimos anos, a empresa A manteve-se em crescimento: no 1º ano obteve lucro de
R$ 100.000,00; após 2 anos obteve lucro de 110.000,00: após 3 anos, 120.000,00;
e assim por diante. A empresa B também se manteve em crescimento: no 1º ano
obteve lucro de R$ 20.000,00; após 2 anos, obteve lucro de R$ 40.000,00; após 3
anos, R$ 80.000,00; e assim por diante.
Escreva a sequencia que representa o lucro de cada empresa.
Qual a diferença que se observa entre o crescimento de cada
sequencia?
Situação 3: maria está com problemas de gargante, e para solucionar
seu problema o médico receitou um antiinflamatório de 8 em 8 horas. Maria
iniciou ser tratamento as 15 horas. Escreva a sequencia das 5 próximas
doses de medicamento que a mesma deverá tomar.
Situação 4: Observe o conjunto de figuras que representam os três
primeitos termos de uma sequência.
Mantendo-se este padrão escreva os 3 próximos termos e responda: qual a
relação que há entre o números de retângulos em cada figura?
7.2- Historicização
As progressões foram estudadas desde povos muito antigos como os
babilônicos. Inicialmente, procurou-se estabelecer padrões como o da enchente
do Rio Nilo, onde os egípcios de 5.000 anos atrás tiveram que observar os
períodos em que ocorria a enchente do rio, pois para poderem plantar na época
certa e assim garantir seus alimentos, os egípcios precisavam saber quando
haveria inundação. Havia, portanto, necessidade de se conhecer o padrão desse
acontecimento. Eles observaram que o rio subia logo depois que a estrela Sírius
se levantava a leste, um pouco antes do Sol. Notando que isso acontecia a cada
365 dias, os egípcios criaram um calendário solar composto de doze meses, de 30
dias cada mês e mais cinco dias de festas, dedicados aos deuses Osíris, Hórus,
Seth, Ísis e Nephthys. Os egípcios dividiram ainda os doze meses em três
estações de quatro meses cada uma: período de semear, período de crescimento
e período da colheita. Na Mesopotâmia surgiram várias tabletas babilônicas muito
interessantes, mas nenhuma delas foi tão extraordinária quanto a tableta Plimpton
322 (1900 a 1600 a.C.). Numa dessas tabletas, a progressão geométrica
1+2+2²+...+29 é somada de forma que a série de quadrados 1²+2²+3²+...+10² é
achada. A Matemática no Egito antigo nunca alcançou o nível obtido pela
Matemática babilônica, talvez porque os egípcios tenham se mantido em semi
isolamento, enquanto a babilônia era o centro das rotas de navios, e
consequentemente, era um centro de troca de saberes. No entanto, devemos
lembrar que os egípcios desenvolveram um papel primordial na preservação de
muitos papiros que contribuíram para o nosso conhecimento atual sobre a
Matemática. Em um papiro que data de 1950 a. C. podemos encontrar alguns
problemas teóricos a respeito de Progressões Aritméticas e Geométricas.
7.3- Operacionalização da aula
Para a execução da aula será disponibilizado online a apostila com o
conteúdo a ser trabalhado em sala de aula.
Problematização do conteúdo em diferentes situações
Breve historicização sobre sequências P.A e P.G;
Apresentação dos conteúdos;
Avaliação.
Cada etapa do desenvolvimento da aula será apresentada conforme segue:
Sequências
Uma sequência é uma função f cujo domínio está contido em IN* e cujo
contradomínio é IR.
Em muitas situações da vida diária aparece a ideia de sequência ou
sucessão.


A sequência dos dias da semana (domingo, segunda,..., sábado);
A sequência dos meses do ano (janeiro, fevereiro, março,...,
dezembro);
Nessas situações observamos uma certa ordem nos elementos da
sequencia. Esses elementos são chamados termos da sequência. Na sequência
dos meses do ano temos:
1º termo: janeiro, 2º termo: fevereiro, 3º termo: março,..., 12º termo
dezembro.
Se representarmos o 1º termo por 𝒂𝟏 , o 2º termo por 𝒂𝟐 , o 3º termo por 𝐚𝟑 ,
e assim por diante até o termo de ordem n, ou enésimo termo 𝐚𝐧 , essa sequência
pode ser representada por:
(𝒂𝟏 , 𝒂𝟐 , 𝐚𝟑 ,..., 𝐚𝐧 )
Determinação de uma sequência numérica
Uma sequência numérica pode ser determinada por uma lei de formação,
ou seja, uma lei que associe a cada número natural n diferente de zero um termo
𝑎𝑛 = f(n).
Para determinar uma sequência de números naturais ímpares, pode-se
utilizar a seguinte lei de formação: f (n)  2n  1 , em que n  IN  .
Progressão Aritmética (PA)
Uma PA é uma sequencia numérica em que cada termo, a partir do
segundo é obtido somando – se ao anterior uma constante r, intitulada razão da
PA.
Exemplos:
 (-7, -4, -1, 2, 5,...) é uma PA sua razão é: r = 𝑎2 - 𝑎1 = -4 – (-7) = 3,
PA crescente;
 (32, 12, -8,...) é uma PA, sua razão é: r = 𝑎2 - 𝑎1 = 12 – 32 = - 20,
PA decrescente;
 (6, 6, 6, 6,...) é uma PA infinita, sua razão é: r = 𝑎2 - 𝑎1 = 6 – 6= 0,
PA constante.
Representações da PA
Por meio das representações especiais de uma PA, podemos diminuir a
quantidade de cálculos exigidos em algumas situações.

Três termos em PA: (x – r, x, x + r);
Termo geral de uma PA
𝑎𝑛 = 𝑎1 + (n – 1)r
Onde: 𝑎𝑛 = termo geral ou o n-ésimo termo, n = número de termos (até 𝑎𝑛 ), 𝑎1 =
primeiro termo, r = razão da PA.
Exemplos:
1) Qual é o 20º termo da PA (2, 8,...)?
𝑎1 = 2
r=8–2=6
n = 20
𝑎20 = 𝑎1 + 19.r = 2 +19 x 6 = 116
2) Quantos múltiplos de 6 existem entre 4.000 e 5.000?
A sequencia dos múltiplos de 6 é uma PA de razão 6. O primeiro múltiplo de 6
existente nesse intervalo é 𝑎1 = 4.002 e o ultimo é 𝑎𝑛 = 4.998. substituindo esses
valores na expressão
𝑎𝑛 = 𝑎1 + (n – 1)r, obtemos:
4.998 = 4.002 + (n – 1). 6 → n = 167
Portanto existem 167 múltiplos de 6 entre 4.000 e 5.000.
Agora vamos retornar as nossas situações 2, 3 e 4 do inicio de nossa aula.
Soma dos n primeiros termos de uma PA
𝑠𝑛 =
𝑛(𝑎 1 + 𝑎 𝑛 )
2
Demonstração utilizando o raciocínio de Gauss:
Exemplos:
1) Calcular a soma dos 60 primeiros números naturais.
A sequência dos números naturais forma uma PA de razão 1 e primeiro termo
igual a 0.
Assim, 𝑎60 = 𝑎1 + 59r → 𝑎60 = 0 + 59 x 1 → 𝑎60 = 59
𝑠60 =
60.( 𝑎 1 + 𝑎 60 )
2
→ 𝑠60 =
60.(0+59)
2
→ 𝑠60 = 1.770
2) Calcular a soma dos 10 primeiros números impares.
Assim, 𝑎10 = 𝑎1 + 9𝑟 → 𝑎10 = 1 + 9 ∙ 2 → 𝑎10 = 19
10 ∙ (1 + 19)
𝑠10 =
→ 𝑆10 = 100
2
A soma dos números impares corresponde a um n qualquer 𝒂𝒏 = 𝒏𝟐 , com n Є
IN*.
Exercícios
1) Em cada caso abaixo, determine x de modo que a sequência seja uma PA:
a) (2x, x + 5, 4x)
b) (x – 1, -3x, 5x + 1)
c) (-2, x² + 2, 7x + 1)
2) quantos termos possui a PA (4,7,..., 91)?
Progressão Geométrica (PG)
PG é uma sequência numérica que em cada termo, a partir do segundo, é obtido
multiplicando-se o anterior por uma constante q chamada razão da PG.
Para uma PG de termos não nulos:
q=
𝑎2
𝑎1
=
𝑎3
𝑎2
=
𝑎4
𝑎3
=⋯=
𝑎𝑛
𝑎 𝑛 −1
Exemplos:
No processo de divisão celular por mitose cada célula de divide originando outras
duas conforme a imagem
Se o processo continua qual a sequência que representa o
número de células originadas em cada etapa da divisão?
Qual a razão que existe em cada etapa?
Outros exemplos:

(- 2, - 4, - 8, -16,...) é uma PG, sua razão é: q =

(1, - 3, 9, - 27,...) é uma PG, sua razão é: q =
𝑎2
𝑎1
𝑎2
𝑎1
=
=
−4
−2
−3
1
= 2;
= - 3.
Classificação de uma PG
Dependendo da razão q uma PG pode ser:
 Crescente: a PG é crescente quando q > 1 e os termos são positivos ou
quando 0 < q < 1 e os termos são negativos.
Exemplo: (2, 6, 18, 54,...) com q = 3
1
(-40, -20, -10, -5, ...) com q =
2

Decrescente: A PG é decrescente quando 0 < q < 1 e os termos são
positivos ou quando q > 1 e os termos são negativos.
Exemplo: (200, 100, 50, 25,...) em que q =1/2
(-4, -12, -36, -108,...) em que q = 3

Constante: A PG é constante quando q = 1.
Exemplo: (10, 10, 10, 10,...) em que q = 1
(-5, -5, -5, -5,...) em que q = 1.

Alternante: A PG é alternante quando q < 0.
Exemplo: (4, -8, 16, -32,...) em que q = -2;
(-81, 27,-9, 3,...) em que q = -1/3.
Termo geral da PG
𝑎𝑛 = 𝑎1 𝑞 𝑛−1
Exemplo:
1) Determinar o oitavo termo da PG (-3, 18, -108,...)
𝑎1
= -3, n = 8 e q =
𝑎8 = (-3).(−6)8−1
−108
= -6, agora basta aplicar a fórmula:
18
→ 𝑎8 = 839.808.
Soma dos n primeiros termos de uma PG finita
𝑠𝑛 =
𝑎 1 . (𝑞 𝑛 −1)
𝑞−1
Demonstração da fórmula:
Exemplos:
1) Calcular a soma dos sete primeiros termos da PG (6, 18, 54, ...)
𝑎1 = 6 e q = 3.
6∙ (37 −1)
𝑠7 =
3−1
→ 𝑠7 =
6∙ (37 −1)
2
→ 𝑠7 = 3 ∙ (37 − 1) → 𝑠7 = 38 -3
𝑠7 = 6.561 − 3 → 𝑠7 = 6.558.
Exercícios
1) Numa PG de razão igual a 2, a soma dos sete primeiros termos é 635. Calcule
o primeiro termo.
2) em cada caso abaixo, determine x de modo que a sequencia seja um PG:
a) (9, x, 4)
b) (x+4, x+20, x+68)
Conclusão da aula:
Questionar os alunos para ver se os objetivos foram alcançados, buscando a
comprovação nos exemplos em sala de aula e na prova.
8- Avaliação
8.1 Instrumentos de avaliação
Prova do conteúdo abordado
9- Referências
BARROSO, Juliane Matsubara. Conexões com a matemática. 1. Ed. São Paulo:
Moderna, 2010.
DANTE, Luiz Roberto. Tudo é matemática. 3. Ed. São Paulo. Editora Ática, 2011.
LIMA, Valéria scomparim. História, conceito e aplicações sobre PA e PG.
<http://matematica-online-clc.blogspot.com.br/2009/05/historia-conceitos-eaplicacoes-sobre.html>. Acesso em: 13 set. 2014.