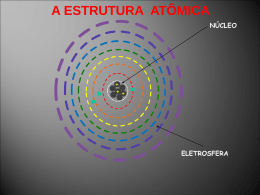
Eletricidade
O início
Eletricidade
• Século VI a.C.
• Grécia Antiga
• Tales de Mileto
Quando?
Onde?
Quem?
ATRITO
Pele de Animal
Ou Tecido
Âmbar
Elektron = Âmbar
Eletricidade
Tales de
Mileto
600 a.C.
Willian Benjamin
Gilbert Frankling
Cristo
Ano 0
Cargas elétricas positivas
Raios são Fenômenos Elétricos
1600
Inglaterra
+
1750
EUA
e negativas
Hoje
-
Eletricidade pode ser transferida
entre corpos.
Invenção do Pára-Raios
Eletricidade
ELETRICIDADE
Eletrostática
Eletrodinâmica
Estudo de Cargas Elétricas
em Repouso
Estudo de Cargas Elétricas
em Movimento
Eletromagnetismo
Estuda o efeito produzido
pela movimentação das
cargas elétricas.
Eletrostática
Você já ouviu falar em Eletricidade estática?
PENSE NISSO!
Explosão em postos
de Gasolina
Carro de Corrida
ao abastecer
Formação
dos raios.
Choque ao
sair do carro.
Já reparou nesses detalhes?
Eletrostática
Eletrosfera
Elétrons – Carga Negativa
Átomo
Neutro
Um átomo NEUTRO é aquele
que possui a mesma quantidade
de elétrons e prótons.
Prótons – Carga Positiva
Nêutrons – Compõem a massa da matéria
Alguns materiais possuem facilidade para trocar
elétrons com os átomos vizinhos, e outros não.
Eletrostática
A falta ou excesso de elétrons deixa o corpo carregado.
Átomos
Eletrizados
Carregado Positivamente
Mais prótons do que elétrons
Carregado Negativamente
Mais elétrons do que prótons
Quanto mais átomos desequilibrados, maior a carga do corpo.
A unidade de medida de Carga Elétrica é o
Coulomb [C]
Eletrostática
Corpos carregados com cargas de sinal igual, SE REPELEM.
Corpos carregados com cargas de sinais opostos , SE ATRAEM.
Positivo
Positivo
Negativo
Negativo
Positivo
Negativo
• PINTURA ELETROSTÁTICA A PÓ
• Revestimento em pó nas versões epóxi, poliéster e
híbrido.
O pó adere perfeitamente às peças mesmo em
pontos de difícil acesso, como cavidades,
reentrâncias e etc.
• Após a aplicação, quando a peça é submetida ao
aquecimento, as partículas de pó aderidas se fundem
formando uma película plástica uniforme, com
espessuras que variam de 40 a 100 microns. Essa
película não amolece mesmo quando submetida a
reaquecimento. O tempo de cura varia de 10 a 30
minutos, a temperatura entre 150°C a 200°C.
Fotocopiadoras
Um cilindro foto-sensível polarizado positivamente é carregado com a imagem
refletida do original através de espelhos, dessa forma a região iluminada
(espaços vazios da imagem) perde a carga elestrostática.
O toner (tinta em pó) carregado negativamente é atraído pelo cilindro, que gira
contra o papel imprimindo a imagem.
Por último, o papel é aquecido para que haja a fixação da tinta.
Eletrostática
Carga Elétrica
Propriedade física dos prótons e elétrons.
Carga Elementar [e]
É a mínima carga possível em um corpo qualquer.
e = 1,6.10-19 C
A carga total [Q] em um corpo é dada pela quantidade de elétrons
que faltam (ou sobram) multiplicado pelo valor da carga elementar:
Q=nxe
Onde:
Q = Carga Total do Corpo considerado;
n = Número de elétrons
e = Carga elementar = 1,6.10-19C
Se faltam elétrons, Q positivo
Se sobram elétrons, Q negativo
Eletrostática
Exemplos
1. Considere uma esfera de borracha que perde 4000 elétrons após um processo de
fricção. Qual é a carga elétrica acumulada neste corpo?
Aplicando-se a fórmula anterior:
Q=n.e  Q= 4000 x 1,6.10-19C   Q = + 6,4.10-16C
É positivo porque perdeu elétrons
2. Qual a carga armazenada por uma esfera de nylon, inicialmente neutra, que adquiriu
10.625.000 elétrons de um outro corpo carregado?
Como o corpo recebeu elétrons, então a carga é negativa.
Q= - n.e  Q= - 10.625.000 x 1,6.10-19C   Q = - 1,7.10-12C
É negativo porque ganhou elétrons
Q= - 1,7pC
Exercícios
• Resolva os exercícios da página 5 da sua
apostila.
Eletrostática
Condutores e Isolantes
Barra de Vidro atritada em lã:
Atritando a ponta
do bastão.
Aproximando-se papel (por exemplo) da ponta do bastão, ocorrerá atração.
Porém, se aproximarmos o papel do meio do bastão, nada ocorre.
Somente a ponta do bastão ficou eletrizada.
Por outro lado, se atritarmos um bastão de ferro, as cargas acumuladas na ponta
desse bastão percorrerão facilmente o corpo, e serão conduzidos a qualquer
outro corpo que estiver em contato, por exemplo, a mão que segura o bastão.
Se segurarmos o bastão de metal por um barbante, por exemplo, haverá eletrização.
Eletrostática
Condutores e Isolantes
Definições:
Condutor: Material cujos átomos possuem facilidade de trocar
elétrons com os átomos vizinhos.
Isolante: Material cujos átomos possuem dificuldade de trocar
elétrons com os átomos vizinhos.
= Dielétrico
Podemos comparar a
Um tubo cheio d’água
Podemos comparar a
Um tubo cheio de areia
Eletrostática
Condutores e Isolantes
Lembre-se do exemplo do caminhão de gasolina:
A carcaça do caminhão é condutora, porém, toda a estrutura é
isolada do solo através dos pneus de borracha.
Enquanto o caminhão está em movimento, está em
constante atrito com o ar, Acumulando energia estática.
Quando conecta-se a mangueira do caminhão ao tanque
subterrâneo do posto, essa energia é transferida à terra,
gerando uma faísca.
Procedimento padrão: aterrar o caminhão
antes de abrir o compartimento de carga para
descarregar a carga acumulada.
Eletrostática
Condutores e Isolantes
Agora o exemplo do Helicóptero:
Ao Abastecer:
Foto: [email protected]
Eletrostática
Agora temos conhecimentos
suficientes para estudar a
Eletrodinâmica!
Eletrodinâmica
Dinâmica = Movimento
Quando temos 2 corpos carregados, um deles positivamente, e o outro
negativamente, diz-se que existe uma diferença de potencial elétrico entre eles.
ddp = 0
Os elétrons do corpo negativo “desejam” ocupar
as lacunas do corpo positivo, neutralizando os dois corpos.
As 3 grandezas fundamentais são :
Tensão Elétrica (ou ddp ou fem): é a força que impulsiona os elétrons de um corpo a
outro.
Corrente Elétrica: é o fluxo ordenado dos elétrons em uma certa direção.
Resistência Elétrica: é a oposição à passagem dos elétrons.
Eletrodinâmica
Tensão Elétrica, Diferença de Potencial (ddp) ou Força Eletromotriz (fem):
força que impulsiona os elétrons de um corpo a outro.
Fontes de Alimentação:
Atenção ao descarte
consciente
Eletrostática
Resistência Elétrica
Condutores
Isolantes
Ferro
Borracha
Alumínio
Polímeros (plásticos)
Ouro
Madeira
Cobre
Nylon
A classificação de um material depende
da sua Resistividade.
Resistividade é uma característica dos
materiais que indica a facilidade do
material desprender elétrons da
camada de valência dos átomos.
Quanto mais alta a resistividade, mais
isolante é o material. Quanto menor a
resistividade, melhor condutor é o
material.
Material
Resistiviade r (W.m)
Condutores
Prata
1,58´ 10-8
Cobre
1,67´ 10-8
Alumínio
2,65´ 10-8
Tungstênio
5,6´ 10-8
Ferro
9,71´ 10-8
Semicondutores
Carbono (grafite)
(3 - 60) ´ 10-5
Germânio
(1 - 500) ´ 10-3
Silício
0,1 - 60
Isolantes
Vidro
109 - 1012
Borracha
1013 - 1015
Eletrostática
Resistência Elétrica
Depende das dimensões do corpo.
[Ω]
ρ = Resistividade do
material
R = Resistência
ρ = Resistividade
l = Comprimento
A = Área da secção transversal (m2)
A = Área da secção transversal
Eletrostática
Resistência Elétrica
Depende da temperatura do corpo.
R2= R1.[1+  . (T2 – T1)]
R2 = Resistência na temperatura 2
R1 = Resistência na temperatura 1
α = Coeficiente de temperatura do material
T1 = Temperatura referência
T2 = Nova Temperatura
[Ω]
Exercícios
• Resolva os exercícios da página 11 da sua apostila.
Eletrodinâmica
Unidades de Medida
Tensão (E)  Volt (V)
Corrente (I)  Ampére (A)
Resistência (R)  Ohm (Ω)
Fonte de Tensão E
Corrente I
Resistência R
5A
220Ω
Símbolo
Símbolos
+
3V
Símbolo
Pilhas, baterias,
carregadores,
Fontes de
aparelhos, etc.
Voltímetro
V
Resistores, Lâmpadas,
Resistência de Chuveiro,
Motores, etc.
Medidor
Amperímetro
A
Ohmímetro
Ω
Eletrodinâmica
Circuito Elétrico
É o arranjo que utiliza energia elétrica para realizar algum tipo de trabalho.
Diferença de Potencial 
Tensão Elétrica (pilha)
E +
-
Lâmpada
Acende
Corrente
Elétrica
I
Resistência
Elétrica
R
As três grandezas estão relacionadas pela LEI DE OHM
A corrente é diretamente
Proporcional à tensão
E inversamente proporcional
À resistência.
E
I= E
R
.
R
x
I
Exercícios
• Resolva os exercícios da página 13 da sua apostila.
Eletrodinâmica
O Resistor
Eletrodinâmica
Resistores Variáveis
RAC + RCB = RAB
Eletrodinâmica
Código de Cores de Resistores
*
Cor
1ª faixa
2ª faixa
3ª faixa
Multiplicador
Tolerância
Preto
0
0
0
100
Marrom
1
1
1
101
± 1%
Vermelho
2
2
2
102
± 2%
Laranja
3
3
3
103
± 3%
Amarelo
4
4
4
104
± 4%
Verde
5
5
5
105
Azul
6
6
6
106
Violeta
7
7
7
107
Cinza
8
8
8
108
Branco
9
9
9
109
Dourado
-
-
-
10-1
± 5%
Prata
-
-
-
10-2
± 10%
Sem cor
-
-
-
-
± 20%
Eletrodinâmica
E-12
10
Valores
Preferenciais de
Resistores
12
15
18
22
27
33
39
47
56
68
82
E-24
E-96
10
100
178
316
562
11
102
182
324
576
12
105
187
332
590
13
107
191
340
604
15
110
196
348
619
16
113
200
357
634
18
115
205
365
649
20
118
210
374
665
22
121
215
383
681
24
124
221
392
698
27
127
226
402
715
30
130
232
412
732
33
133
237
422
750
36
137
243
432
768
39
140
249
442
787
43
143
255
453
806
47
147
261
464
825
51
150
267
475
845
56
154
274
487
866
62
158
280
499
887
68
162
287
511
909
75
165
294
523
931
82
169
301
536
953
91
174
309
549
976
Eletrodinâmica
Potência Elétrica
Relaciona trabalho com o tempo
P=E.I
watts  W
P=R.I.I
P=E.E
R
P = R . I2
P = E2
R
E
R
x
E= 110V
E= 220V
60W
I = 545,45mA
I = 272,73mA
100W
I = 909,09mA
I = 454,55mA
I
Exercícios
• Resolva os exercícios da página 18 da sua apostila.
Eletrodinâmica
Associação de Resistores
1. Associação em Série
REQ = R1 + R2 + R3 + ... + Rn
2. Associação em Paralelo
Exercícios
• Resolva o exercício 1 da página 20 da sua apostila.
Eletrodinâmica
Associação de Resistores
I = 100mA
A
+
R = 120Ω
E = 12V
-
V
+
12V
Queda de
Tensão
Eletrodinâmica
Associação de Resistores
ER1 = R1 x I1
+
I = 50mA
ER1= 120Ω x 50mA
A
ER1 = 6V
R1 = 120Ω
V
E = 12V
-
R2 = 120Ω
+
6V
Queda de
Tensão
+
E
V
=R xI
R2
2
2
6V
Queda de ER2= 120Ω x 50mA
Tensão
ER2 = 6V
Eletrodinâmica
Associação de Resistores
I = 100mA
A
+
R = 120Ω
E = 12V
-
V
+
12V
Queda de
Tensão
Eletrodinâmica
Associação de Resistores
-
R1
120Ω
I2= 100mA
E = 12V
+
I1= 100mA
I = 200mA
R2
120Ω
VR2 = 12V
VR1 = 12V
Exercícios
• Resolva o exercício 2 da página 20 da sua apostila.
Eletrodinâmica
Leis de Kirchhoff
Lei das Malhas (ou Lei das Tensões)
“A somatória algébrica das tensões ao longo de uma malha é Nula.”
ΣV = 0
Entende-se por malha, um circuito fechado, incluindo vários componentes elétricos, como
resistores e fontes de tensão.
+
+
EFonte = 12V
Sentido da
Malha
E1= 5V
-
+
E2= ?
Regra: A seta que coincide com o sentido da Malha, é Positiva;
A seta contrária ao sentido da Malha, é Negativa.
EFonte + (- ER1) + (- ER2) = 0
EFonte – ER1 – ER2 = 0
12V – 6V – 6V = 0
0 = 0  OK!
Exercícios
• Refaça os exercícios anteriores da sua
apostila (a, b e c), calculando as quedas de
tensão em cada componente.
Eletrodinâmica
Outro Exemplo
Calcule o Valor da tensão entre os pontos P e Q.
1º passo: adotar sentido da malha (M1)
2º passo: adotar
quedas de tensão
sentido
das
Componentes passivos, sentido de
negativo para positivo.
Eletrodinâmica
Calcule o Valor da tensão entre os pontos P e Q.
VPQ = - E3 – VR3 + E2
VPQpasso:
= - 3Vadotar
– (2Ω.3,33A)
1º
sentido +da18V
malha (M1)
VPQ = -3V - 6,66V + 18V
2º
adotar sentido das quedas
VPQpasso:
= 8,34V
de tensão
3º passo: adotar ponto de referência
-E3 – VR3 + E2 + VR2 – E1 – VR1 = 0
-3V – R3.I3 + 18V + R2.I2 – 5V – R1.I1 = 0
I1 = I2 = I3 = I
4º passo: realizar a soma algébrica
das tensões de toda a malha
considerando o sentido adotado
5º passo: resolver a equação,
descobrir valor da corrente (I) e
10V – 2Ω.I + 1Ω.I – 2 Ω.I = 0
determinar o valor da tensão entre os
pontos P e Q.
10V – 3Ω.I = 0
-3V – R3.I3 + 18V + R2.I2 – 5V – R1.I1 = 0
-3V – 2Ω. 3,33A + 18V + 1Ω.3,33A – 5V – 2 Ω.3,33A = 0
I = 10V / 3Ω
-3V - 6,66V + 18V + 3,33V – 5V - 6,66V = 0
I = 3,33A
-9,66V + 21,33V - 11,66 = 0
-3V – 2Ω.I + 18V + 1Ω.I – 5V – 2 Ω.I = 0
Eletrodinâmica
Exemplo Prático
Calcule o Valor da tensão da fonte.
Eletrodinâmica
Leis de Kirchhoff
Lei dos Nós (ou Lei das Correntes)
“A somatória das correntes que entram em um nó é igual a somatória das
correntes que saem desse mesmo nó.
ΣI entram = ΣI saem
Entende-se por nó, o ponto de encontro de três ou mais ramos de um circuito, tendo cada
ramo um ou mais componentes elétricos.
Exercícios
• Resolva os exercícios da sua apostila.
Exercícios
• Resolva os exercícios da sua apostila.
IT
I1
I2 = IT .
R1
R1 + R2
R1
R2
30V
I2