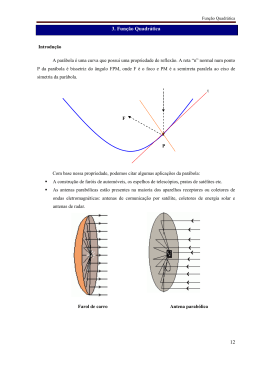
A Propriedade do Foco de uma Parábola
Concepção Principal
Em matemática, um locus é um conjunto de pontos cuja a localização satisfaz as condições
especificas. Se marcamos um ponto P,chamado de foco e uma linha l chamada diretriz, que não passa
por P ,o lugar geométrico dos pontos eqüidistantes de P e L, foma uma parábola. Em outras palavras, é
o gráfico de uma equação quadrática.
O local de pontos eqüidistantes de P e L em forma de parábola. Em outras palavras, é o gráfico de uma
equação quadrática.
Explicando
Suponha que o ponto P possua Coordenadas Cartesianas
contém a equação
e l é uma reta horizontal que
. Podemos fazer isso sem perda de generalidade, basta somente girar o
sistema coordenadas de forma correta. Agora escolher qualquer ponto no plano de coordenadas
gerais
.
A distância P a
A distância l a
é dada por
é dada por
Assim, igualando essas distâncias e resolvendo para y, veremos:
.
.
Desde que todas as variáveis indexadas são constantes, ou seja, simplesmente uma equação
quadrática provando que o local de pontos eqüidistantes de P e L formam uma parábola.
Clique e arraste o ponto vermelho na trama a seguir para definir o foco, P, e use o controle
deslizante para alterar a posição da diretriz l.
Em seguida, escolha o botão "Localizar pontos eqüidistantes" e clique sobre o gráfico de
acrescentar alguns pontos que são eqüidistantes de P e L.
Use a caixa de seleção "Mostrar Parábola" para traçar a parábola e ver a sua equação. Clique em
"Limpar" para limpar o gráfico.
Ajustar Ponto e Reta
Encontrar Pontos ...
Distância onde P para
Ultimo Ponto =
Distância de l para o Último
Ponto =
Mostrar Parábola
Equação da parábola:
10
5
Limpar
0
Posição da reta
-5
-10