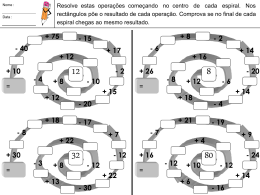
Distância
Arquivo de Entrada: distancia.in
Arquivo de Saída: distancia.out
Tempo Máximo de Execução: 60 s
Uso Máximo de Memória: 32 MB
Descrição
Por um bom tempo os matemáticos têm provado a característica enumerável de conjuntos
numéricos.
Um conjunto A é enumerável se existe uma correspondência de um para um entre todos os seus
elementos e os números naturais
. Tais conjuntos também são chamados contáveis. Esta
correspondência é geralmente definida por meio de uma função bijetora f :
A.
O conjunto Z Z é enumerável, e uma das correspondências é ilustrada abaixo, em uma espiral de
Con Petius.
Este problema consiste em, dadas duas posições de pontos na espiral de Con Petius, determinar a
distância Euclidiana entre estes pontos no plano cartesiano correspondente ao mapeamento Z Z .
A distância Euclidiana entre dois pontos a ( x a , y a ) e b ( xb , y b ) é dada por:
d ( A, B)
( xb
xa ) 2
( yb
ya ) 2 .
Entrada
A primeira linha do arquivo contém a quantidade q de pares de pontos na espiral de Con Petius a
serem analisados (0 q 10000) . A seguir seguem q pares de pontos, cada par em uma linha. Em
cada linha, os pontos a e b estão separados por um espaço (0 a b 2 31 1) .
Exemplo do arquivo de entrada (distancia.in):
3
0 1
0 2
4 8
Saída
Para cada par de pontos na espiral de Con Petius no arquivo de entrada, há uma linha no arquivo de
saída com a distância real entre os pontos. Esta distância deverá ser escrita como uma raiz
e
e
e
e
simplificada t p , tal que p p 0 0 . p1 1 . p 2 2 ... p n n é a fatoração de p com p 0 p1 p 2
pn e
i,0 i n, pi é primo ai 1 . Note que, para números irracionais, só é necessário escrever t se
este é diferente de 1 e, para números racionais, somente se escreve t.
Como não é possível utilizar uma representação matemática elaborada em um simples arquivo de
texto, a seguinte notação para t p a ser utilizada será t * sqrt p, com um espaço entre cada
termo.
Exemplo do arquivo de saída correto para a entrada dada (distancia.out):
1
sqrt 2
2 * sqrt 2
This document was created with Win2PDF available at http://www.daneprairie.com.
The unregistered version of Win2PDF is for evaluation or non-commercial use only.