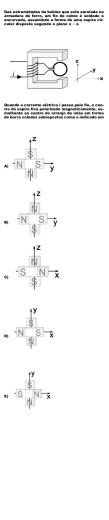
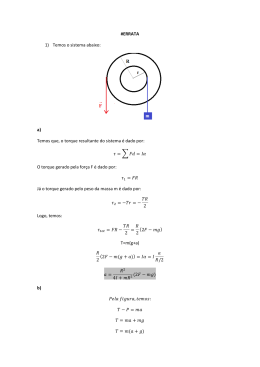
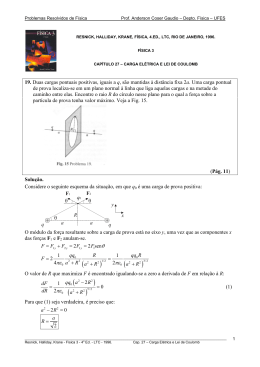
Problemas Resolvidos de Física
Prof. Anderson Coser Gaudio – Depto. Física – UFES
RESNICK, HALLIDAY, KRANE, FÍSICA, 4.ED., LTC, RIO DE JANEIRO, 1996.
FÍSICA 3
CAPÍTULO 34 – O CAMPO MAGNÉTICO
51. Um fio de comprimento L conduz uma corrente i. Mostre que se o fio forma uma bobina
circular, o torque máximo desenvolvido por um determinado campo magnético acontece quando
a bobina tem apenas uma espira e seu módulo é dado por
τ=
1 2
L iB .
4π
(Pág. 153)
Solução.
Como o comprimento do fio é fixo, quanto maior o número de espiras menor será a área de cada
uma. O comprimento do fio (L) deve ser igual ao número de voltas (N) vezes o comprimento de
cada volta (2πr).
L = 2π rN
L
(1)
r=
2π N
O torque da força magnética sobre a espira vale:
τ= μ × B
τ = NiABsenθ
τ = Ni (π r 2 ) Bsenθ
Naturalmente o ângulo θ deverá ser igual a π/2 para maximizar o torque:
τ = π Nir 2 B
Substituindo-se (1) em (2):
(2)
2
 L 
τ = π Ni 
 B
 2π N 
iL2 B
4π N
Como τ ∝ 1/N, conclui-se que para maximizar o torque o número de espiras deverá ser o menor
possível, ou seja, igual a 1 (N = 1).
τ=
τ=
iL2 B
4π
________________________________________________________________________________________________________
Resnick, Halliday, Krane - Física 3 - 4a Ed. - LTC - 1996.
Cap. 34 – O Campo Magnético
1