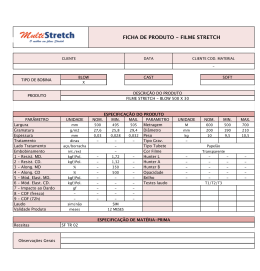
O sistema abaixo foi idealizado para a determinação das pressões dos gáses A, B e C. Sabendo-se que o mesmo encontra-se em repouso e que a
leitura barométrica é 702 mmHg, pede-se determinar a pressão dos gases, tanto na escala efetiva como na absoluta. (valor - 2,5)
Área A
Dados:
F
F = 50 kgf → A = 50 cm 2
kgf
kgf
γ H 2 O = 1000
→ γ Hg = 13600
m3
m3
Gás C
respiro
Gás A
0,25m
H 2O
2,3m
Hg
Gás B
H 2O
1
Pelo conceito de pressão e considerando que o pistão encontra-se em
equilíbrio, tem-se: pgás
C
=
kgf
kgf
F 50kgf
=
=
1
=
10000
A 50cm 2
cm 2
m2
Por outro lado pela equação manométrica se pode escrever que:
pgás + 0,25 × 13600 = 10000 ∴ pgás
A
A
= 6600
kgf
m2
Finalmente: 6600 + 2,3 × 1000 = pgás ∴ pgás = 8900
B
B
Evocando-se
a
relação
entre
a
escala
kgf
m2
absoluta
e
efetiva:
pabs = pefetiva + patm
, pode-se determinar as pressões anteriores na
local
escala absoluta, a qual deve ser sempre caracterizada pelo símbolo abs,
sendo a única exceção a pressão atmosférica, já que esta na escala efetiva
vale sempre zero.
kgf
pgás
= 6600 + 0,702 × 13600 = 16147,2
pgás
= 8900 + 0,702 × 13600 = 18447,2
pgás
= 10000 + 0,702 × 13600 = 19547,2
Aabs
Babs
Cabs
m2
kgf
m2
kgf
m2
2
Um êmbolo de diâmetro 400 mm e comprimento 500 mm pela ação da
gravidade deliza no interior de um tubo vertical de diâmetro interno igual a
402 mm. O espaço entre a superfície lateral do embolo e a superfície
interna do tubo é uniformemente preenchido com óleo lubrificante de
viscosidade igual a 10 −3
2
N×s
m2
. Se o êmbolo atinge a velocidade constante de
m
, pede-se especificar o peso do êmbolo. (valor - 2,5)
s
500 mm
óleo
lubrificante
movimento
Solução: como a velocidade é constante pode-se escrever:
∴ G = Fµ = µ ×
∴ G = 1,26N
∑F = 0
v
2
× Acontado = 10 − 3 ×
× π × 0,4 × 0,5
402
400
−
ε
(
)
2
3
Um certo fenômeno é caracterizado pelas variáveis: aceleração da
gravidade (g); massa específica ( ρ ); velocidade (v) e comprimento
característico (L). Adotando-se a base ρ vL pede-se determinar o(s)
adimensional(is) (Valor - 2,0)
Solução: aplicando-se o teorema dos π :
1. n = 4
[g ] =
2.
L × T −2
[ρ ] = F × L − 4 × T 2
[v ] = L × T − 1
[L ] =
L
3. k – 3
4. m=n-k = 4-3 = 1
5. base - ρ vL
π1 = ρ α1 × v α 2 × Lα 3 × g
F 0 × L0 × T 0 = (F × L− 4 × T 2 ) α1 × (L × T −1 ) α 2 × Lα 3 × L × T − 2
F 0 × L0 × T 0 = F α1 × L− 4α1 + α 2 + α 3 +1 × T 2α1 − α 2 − 2
6. 0 = α1
− α 2 − 2 = 0 ∴ α 2 = −2
0 = −2 + α 3 + 1∴ α 3 = 1
∴ π1 =
L×g
v2
4
O peso de 3 dm³ de uma substância é 23,5 N. Se g = 9,8 m/s², qual será a
sua massa específica no SI (kg/m³); MK*S (utm/m³) e no CGS (g/cm³)?
(valor - 1,5)
Solução:
kg
m
G
23,5
=
⇒ ρSI =
≅ 799,3 3
3
−
V g×V
9,8 × 3 × 10
m
799,3
utm
ρMK *S =
≅ 81,6 3
9,8
m
ρ=
ρCGS =
799,3 × 103
10
6
≅ 0,8
g
cm3
Um tanque de ar comprimido apresenta volume igual a 2,38 × 10 −2 m 3 .
Determine a massa específica e o peso do ar contido no tanque quando a sua
pressão for 441,3 kPa (abs) e a sua temperatura for 21°C.
m2
Dado: R ar = 287
s2 × K
Solução:
ρ ar =
kg
441,3 × 103
≅ 5,23 3
287 × ( 273 + 21)
m
Gar = ρ ar × Var × g = 5,23 × 2,38 × 10 − 2 × 9,8
Gar ≅ 1,22N
5