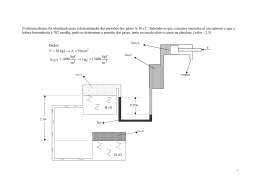
Fluidos, são assim denominados os líquidos e os gases pelo fato de poderem se
escoar com grande facilidade.
Seu estudo teve início com Arquimedes e sua mecânica dos fluídos, responsável
pelo estudo da hidrostática, força gerada por líquidos e gases.
Divisão da Mecânica dos Fluídos
A mecânica dos fluídos foi dividida em duas partes:
Fluído estática – estuda os fluidos em repouso, parados.
Fluído dinâmica – analisa os fluidos que estão em movimento.
MASSA ESPECÍFICA: ρ(Rô) ρ=m/V
VOLUME ESPECÍFICO: v=V/m
PESO ESPECÍFICO: δ=P/V
Densidade
Grandeza Física responsável pela medida da concentração da massa de uma
substância em um determinado volume.
Define-se matematicamente como a razão entre a massa e o volume
correspondentes da substância analisada.
Onde:
d = densidade da substância
m = massa do corpo
V = volume do corpo
A unidade de medida no Sistema Internacional é kg/m³
Densidade (d) ⇒ 0,86 = γf / γ (H2O)
γf= 0,86 x 1.000 (kgf/m3)= 860 (kgf/m3)
γ = ρ.g ⇒ρ = (γ / g) = 860 (kgf/m3) / 9,81 (m/s2 ) = 87,66 (kgf . s2 /m4) ⇒(utm/ m3)
ν = (µ / ρ) ⇒µ = ν×ρ= 0,033 (m2/s)×87,66 (kgf . s2 /m4) = 2,89 (kgf . s /m2)
6)
7)Duas placas planas paralelas estão situadas a 3 mm de distância. A placa superior
move-se com velocidade de 4m/s, enquanto que a inferior está imóvel. Considerando
Pressão
É definida pelo limite da relação de um ponto anterior com a área tendendo a zero.
Esse exemplo indica que mais importante que a força exercida é a área em que a
força atua.
Portanto, a pressão é a divisão entre a intensidade da força F e a área S em que
tal força é distribuída.
Onde:
p = pressão
F = intensidade da força
S = área em que se distribui a força
As unidades de medida no Sistema Internacional são: Pa; ba; 106 dyn / cm²
EXERCÍCIOS:
1)UM LIQUIDO TEM DENSIDADE RELATIVA IGUAL A 0.7. CALCULE A MASSA
ESPECÍFICA PARA ρ H2O =1000KG/M3 E PARA ρH2O=1G/CM3.
0,7=ρ/1000 =
ρ=0,7X1000 = 700
ρ= 0,7 X1 = 0,7
2) DETERMINAR A VISCOSIDADE CINEMÁTICA DO ÓLEO 20 NO
VISCOSÍMETRO DE SAYBOLT PARA UM VOLUME DO ÓLEO DE 60CM3
ESCOANDO NUM DETERMINADO TEMPO.
µ=ρ(0,0022T – 1,8/T)
T= 6 MIN = 6X60S=36S
V=µ/ρ = ρ(0,0022t-1,8/t)/ρ = 0,022x360-1,8/360 = 0,787
V= 0,79 strokes x 100
3) A MASSA ESPECÍFICA DE UM COMBUSTÍVEL LEVE É 805KG/M3.
DETERMINAR O PESO ESPECÍFICO(δ) E A DENSIDADE RELATIVA DESSE
COMBUSTÍVEL.
G=9,8M/S2
PH2O=103KG/M3
δ=P.G
que um óleo ( ν = 0,15 stokes e ρ = 905 kg/m3 ) ocupa o espaço entre elas, determinar a
tensão de cisalhamento que agirá sobre o óleo.
ν = 0,15 stokes = 0,15 cm2/s = 1,50 . 10-5 m2/s
µ = ν×ρ= 1,50 . 10-5 (m2/s) ×905 (kg/m3) = 0,0136 (N. s / m2)
dv
τ = µ [  ]
dy
⇒ τ = µ.[ v0 / e ]⇒τ = 0,0136 (N. s / m2) . [4 (m/s) / 0,003 (m) ] = 18,1 (N/m2)
portanto,
τ = 18,1 Pa
8) A massa específica de um fluido é 610 kg/m3. Determinar o peso específico e a
densidade.
Respostas : 5984 N/m3 e 0,610
9) O peso de 3 dm3 de uma substância é 2,7 Kgf. A viscosidade cinemática é 10-5 m2/s.
Se g é 10 m/s2, determine a viscosidade dinâmica no sistema métrico.
Resposta : 9 x 10-4 Kgf.s/m2
10) Uma placa quadrada de 1 m de lado e 20 N de peso, desliza sobre uma película de
óleo em plano inclinado de 30º. A velocidade da é placa é constante e igual a 2 m/s.
Qual é a viscosidade dinâmica do óleo se a espessura da película é 2 mm ?
Resposta : 0,01 N.s/m2
11) Uma placa retangular de 4 m por 5 m escorrega sobre o plano inclinado da figura,
com velocidade constante, e se apoia sobre uma película de óleo de 1 mm de espessura
e de µ = 0,01 (N. s / m2). Se o peso da placa é 100 N, quanto tempo levará para que a
sua parte dianteira alcance o fim do plano inclinado.
4) Um reservatório graduado contém 500 ml de um líquido que pesa 6 N.
Determinar o peso específico, a massa específica e a densidade do
líquido (considerar g = 9,81 m/s2 ).
Ftang = G . cos(60º) = 100 × 0,50 = 50 N
• Peso Especifico (γ):
V = 500 ml ( 0,50 litro = 0.50 ( 10-3 m3
γ = (G / V) = 6 N / 0.50 ( 10-3 m3 = 12.000 (N/ m3)
• Massa Especifica
(ρ):
γ = ρ.g ( ρ = (γ / g) = 12.000 (N/ m3) / 9,81 (m/s2) = 1.223,2 (kg/m3)
• Densidade (d):
d = γf / γ (H2O) = 12.000 / 9.810 = 1,22
A = 5 × 4 = 20 m2
∆S . cos(60º) = 10 ⇒ ∆S = 20 m
dv
τ = µ [  ]
dy
⇒ τ = µ.[ v0 / e ]⇒τ = ( Ftang / A) ⇒v0 = (Ftang . e / µ . A)
v0 = [ 50 (N) × 0,001 (m) / 0,01 (N. s / m2) × 20 (m2) ] = 0,25 m/s
v0 = (∆S / ∆t) ⇒ ∆t = [ 20 (m) / 0,25 (m/s) ] = 80 s
∆t = 80 s
5) A viscosidade cinemática de um óleo leve é 0,033 m2/s e a sua densidade é 0,86.
Determinar a sua viscosidade dinâmica em unidades dos sistemas Métrico. A peso
específico da água é aproximadamente 1000 kgf/m3.
Viscosidade Dinâmica (µ):