Teoria dos conjuntos
Prof.ª Lúcia Helena de Magalhães
1
CONJUNTOS
1) Introdução:
Analisaremos a seguinte situação problema:
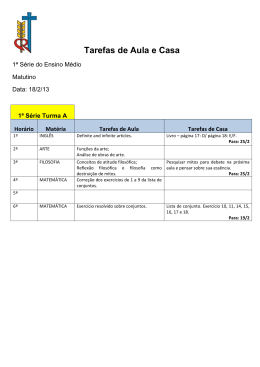
Realiza-se uma pesquisa com 50 pessoas para saber que tipo de atividade física
elas apreciam entre musculação, natação e caminhada, o resultado foi o seguinte: 23
gostam de musculação, 18 de natação e 14 de caminhada; 10 gostam de musculação
e natação; 9 de musculação e caminhada, 8 gostam de natação e caminhada e 5
gostam das três modalidades.
a) Quantas gostam somente de musculação;
b) Quantas gostam só de natação;
c) Quantas não gostam nem de musculação e nem de caminhada;
d) Quantas pessoas gostam só de caminhada ou só natação.
Para resolver questões deste tipo, devemos utilizar conhecimentos de Conjuntos.
2) Noção de Conjuntos:
Toda a Matemática atual é formulada na linguagem de conjuntos. Portanto, a noção de
conjunto é a mais fundamental: a partir dela, todos os conceitos matemáticos podem
ser expressos. Ela é também a mais simples das ideias matemáticas.
Um conjunto é formado por elementos. Dados um conjunto  e um objeto
qualquer a (que pode até mesmo ser outro conjunto), a única pergunta cabível em
relação a eles é:  é ou não um elemento do conjunto  ? No caso afirmativo, diz-se
que  pertence ao conjunto  e escreve-se    . Caso contrário, põe-se   
e diz-se que  não pertence ao conjunto  .
A linguagem dos conjuntos, hoje universalmente adotada na apresentação da
Matemática, ganhou esta posição porque permite dar aos conceitos e às proposições
desta ciência a precisão e a generalidade que constituem sua característica básica.
Vejamos:
Teoria dos conjuntos
Prof.ª Lúcia Helena de Magalhães
2

Conjunto das regiões brasileiras: Norte, Nordeste, Centro-Oeste, Sul e Sudeste.

Conjunto dos estados brasileiros.

Conjunto dos números primos: 2, 3, 5, 7, 11, 13, ...

Conjunto dos números quadrados: 1, 4, 9, 16, 25, 36, ...
Então temos:

R: conjunto das regiões brasileiras,

E: conjunto dos estados brasileiros,

P: conjunto dos números primos,

Q: conjuntos dos números quadrados.
Portanto:

3  P e 8 Q ;

16 Q MinasGer.Sul
Exercícios de Fixação:
Teoria dos conjuntos
Prof.ª Lúcia Helena de Magalhães
3
1) Escreva com símbolos:
a) Colômbia não pertence ao conjunto das regiões brasileiras.
b) Sudeste pertence ao conjunto das regiões brasileiras.
c) 17 pertence ao conjunto dos números primos.
d) 15 não pertence ao conjunto dos números primos.
e) 49 pertence ao conjunto dos números quadrados perfeitos.
f) 38 não pertence ao conjunto dos números quadrados perfeitos.
Resolução:
2) Classifique em verdadeiro (V) ou falso (F):
a) Paraguai  R
b) Nordeste  R
c) 21  P
d) 23  P
e) 20  Q
f ) 64  Q
g) 2  P
h) 55  Q
3) Propriedades, condições e conjuntos:
Os conjuntos substituem as “propriedades” e as “condições”. Consideremos a
propriedade p:
p: x é um número natural ímpar.
Esta propriedade pode ser escrita pelo conjunto M = {1, 3, 5, 7, 9, 11, ...}.
Assim, tanto faz dizer que x possui a propriedade p ou x  M.
Consideremos agora a condição c:
c: x é um número inteiro que satisfaz a condição x² - 4 = 0.
Esta condição pode ser expressa pelo conjunto A = {-2, 2}.
Assim, tanto faz dizer que x satisfaz a condição c ou x  A.
Teoria dos conjuntos
Prof.ª Lúcia Helena de Magalhães
4
4) Igualdade de conjuntos:
Dois conjuntos são iguais quando possuem os mesmos elementos.
Por exemplo: se A = { números naturais ímpares } e B = { 1, 3, 5, 7, 9, 11, ...},
então A = B.
Se A não é igual a B, então A é diferente de B e escrevemos A ≠ B
Exercícios de fixação
3) Escreva o conjunto expresso pela propriedade.
a) x é um número natural ímpar.
b) x é um número natural menor do que 10.
c) x é um número natural múltiplo de 5 e menor do que 31.
d) x é letra da palavra IGUALDADE.
4) Escreva o conjunto dado pela condição:
a) y é um número tal que y² - 25 = 0.
b) y é um número tal que y² - 5y + 6 = 0.
c) y é um número maior que zero e tal que y² - 3y – 10 = 0
d) y é um número divisor de 16 e tal que y³ = 8.
e) y é um número inteiro menor do que 6 e maior que -2.
5) Escreva uma propriedade que define o conjunto:
a) 0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
b) {0, 2, 4, 6}
c) {11, 13 ,15, 17}
d) {0, 1, 2, 3, 4, ..., 99, 100}
5) Conjunto vazio, unitário e universo.
Um conjunto interessante é o conjunto vazio, cuja notação é Ø. Ele é muito útil em
Matemática na simplificação de proposições evitando uma longa e tediosa menção de
exceções. Qualquer propriedade contraditória serve para definir o conjunto vazio.
Por exemplo:
{x I x é um número natural ímpar menor do que 1} = Ø, pois não há um número
natural ímpar menor do que 1.
O conjunto vazio não possui elementos. Podendo ser representado por { }.
Outro conjunto curioso é o conjunto unitário, formado por um único elemento.
Teoria dos conjuntos
Prof.ª Lúcia Helena de Magalhães
5
Exemplo:
{x I x é um número natural par e primo} = {2}, pois o único número par e primo é
o 2.
Observação:
Observe que Ø é diferente de {Ø}, pois {Ø} é um conjunto unitário como único
elemento o conjunto vazio.
O conjunto formado por todos os elementos que estamos trabalhando num
determinado assunto é chamado conjunto universo, cuja notação é U.
Quando atribuímos o universo U, todos os elementos pertencem a U e todos os
conjuntos são partes de U. É muito importante saber em qual universo estamos
trabalhando.
Exemplo:
Se U é o conjunto dos números naturais a equação x + 5 = 0 não tem solução.
Se U é o conjunto dos números inteiros, a equação x + 5 = 0 tem como solução
x = -5.
Exercícios de fixação
6) Classifique como conjunto vazio ou conjunto unitário.
a) A = {polígono que possuem três lados}.
b) B = {x I x é natural maior que 20 e menor que 21}
c) C = {x I x é par maior que 1123 e menor que 1125}.
d) D = {x I x é número primo maior que 11 e menor que 13}
7) Escreva qual é o conjunto universo em cada caso.
a) O triângulo é um polígono de três lados, o quadrilátero é um polígono de quatro
lados e o pentágono, de cinco lados.
b) No conjunto dos números inteiros as soluções da equação x² -16 =0 são -4 e 4.
c) No conjunto dos números naturais a solução da equação x² -16 = 0 é 4.
6) Subconjuntos e relação de inclusão.
Vamos considerar dois conjuntos A e B. Se todos os elementos de A também forem de
B, dizemos que A é subconjunto de B ou que A
está contido em B, ou mesmo que A é parte de B.
Indicaremos como A  B.
A
B
No diagrama ao lado temos:
U
Teoria dos conjuntos
Prof.ª Lúcia Helena de Magalhães
6
Se A não for subconjunto de B, escrevemos A  B.
Exemplos:
1°) Considerando T o conjunto dos números naturais ímpares, e N o conjunto dos
números naturais temos:
T = {1, 3, 5, 7, 9, ...} e N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, ...}
No caso acima, T  N, pois todos os elementos de T pertencem a N.
N
T
2°) Se B é o conjunto dos retângulos e C o conjunto dos quadriláteros, então B  C,
pois todo retângulo é um quadrilátero.
6.1) Relação de inclusão.
Sejam A e B dois conjuntos quaisquer; dizemos que A está contido (ou incluído) em
B, e escrevemos A  B, se todo o elemento de A for elemento de B.
a) A  A pois cada elemento de A pertence a A.
b) Ø  A, qualquer que seja o conjunto A.
A relação de inclusão possui três propriedades básicas. Dados os conjuntos Y, M e P
quaisquer:
b)
Y  Y ( propriedade reflexiva)
Se Y  M e M  Y, então Y = M (propriedade anti-simétrica)
c)
Se Y  M e M  P, então Y  P (propriedade transitiva)
a)
A propriedade anti-simétrica é usada quando queremos provar que dois conjuntos são
iguais.
Exemplo:
Para provar que A = B basta provar que todo elemento de A pertence a B e que
todo elemento de B pertence a A.
A propriedade transitiva é fundamental nas deduções matemáticas.
Por exemplo:
a) N: conjunto dos números naturais,
b) Q: conjunto dos números racionais,
Teoria dos conjuntos
Prof.ª Lúcia Helena de Magalhães
7
c) R: conjunto dos números reais.
Todo número natural é racional.
Todo número racional é real.
Concluímos que, todo numero natural é real.
Se N  Q e Q  R, então N  R.
7) Complemento de um conjunto
O complemento do conjunto B contido no conjunto A, denotado por C A, é a diferença
entre os conjuntos A e B, ou seja, é o conjunto de todos os elementos que pertencem
ao conjunto A e não pertencem ao conjunto B.
CAB = A-B = {x: x
Aex
B}
Graficamente, o complemento do conjunto B no conjunto A, é dado por:
8) Operações com conjuntos
Podemos unir (somar), fazer a intersecção (comparar) e fazer a diferença (subtrair) de
elementos de dois ou mais conjuntos.
Tomemos os conjuntos A = {1, 2, 3, 4, 5} e B = {3, 5, 6, 7} como base para as
operações:
8.1 A união de conjuntos
A UNIÃO dos conjuntos A e B é um novo conjunto contendo todos os elementos de A e
B, ou seja, A
B = {1, 2, 3, 4, 5, 6, 7}.
8.2 A intersecção de conjuntos
Teoria dos conjuntos
Prof.ª Lúcia Helena de Magalhães
8
A INTERSECÇÃO dos conjuntos A e B resulta num novo conjunto contendo apenas os
elementos que são comuns, ou seja, A
B = {3, 5}.
8.3 A diferença de conjuntos
A DIFERENÇA de B com A resulta num novo conjunto contendo os elementos de B
que não pertençam a A, ou seja, B - A = {6, 7}.
9) Conjuntos Numéricos
9.1) Números Naturais
N = { 0 , 1 , 2 , 3 , ... }
9.2) Números Inteiros
Z = { ... , -2 , -1 , 0 , 1 , 2, ... }
OBS: Z* = Z-{0}
Todo número natural é inteiro, isto é, N é um
subconjunto de Z
9.3) Números Racionais
- São aqueles que podem ser expressos na forma a/b, onde a e b são inteiros
quaisquer, com b diferente de 0.
Q ={x/x = a/b com a e b pertencentes a Z
com b diferente de 0 }
Assim como exemplo podemos citar o –1/2 , 1 , 2,5 ,...
-Números decimais exatos são racionais
Teoria dos conjuntos
Prof.ª Lúcia Helena de Magalhães
9
Pois 0,1 = 1/10
2,3 = 23/10 ...
- Números decimais periódicos são racionais.
0,1111... = 1/9
0,3232 ...= 32/99
2,3333 ...= 21/9
0,2111 ...= 19/90
9.4) Números Irracionais
- São aqueles que não podem ser expressos na forma a/b, com a e b inteiros e b
diferente de 0.
-São compostos por dízimas infinitas não periódicas.
Exs:
9.5) Números Reais
-
É a reunião do conjunto dos números irracionais com o dos racionais.
Resumindo:
O
diagrama mostra a relação entre os conjuntos
numéricos.
N  Z  Q  R
Teoria dos conjuntos
Prof.ª Lúcia Helena de Magalhães
10
Portanto, os números naturais, inteiros, racionais e irracionais são todos números
reais.
Obs: entre dois números inteiros existem infinitos números reais. Por exemplo:

Entre os números 1 e 2 existem infinitos números reais:
1,01 ; 1,001 ; 1,0001 ; 1,1 ; 1,2 ; 1,5 ; 1,99 ; 1,999 ; 1,9999 ...

Entre os números 5 e 6 existem infinitos números reais:
5,01 ; 5,02 ; 5,05 ; 5,1 ; 5,2 ; 5,5 ; 5,99 ; 5,999 ; 5,9999 ...
Exercícios de Fixação
9) Usando os símbolos  e  , relacione os conjuntos numéricos a seguir:
a) N e N*
b) Q e R
10) Com os conjuntos numéricos dados, efetue as operações de união e intersecção:
a) Z e Q
b) Q e Ir
11) Determine:
a) N
Z
Teoria dos conjuntos
b) (N
Q) U Z
e)(Q
Prof.ª Lúcia Helena de Magalhães
Ir)
N
11