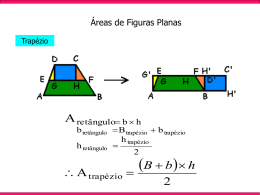
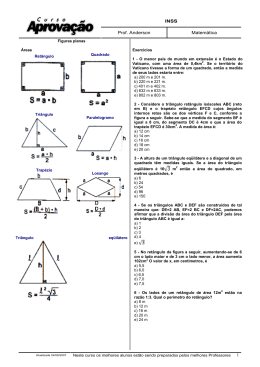
MATEMÁTICA - 1o ANO
MÓDULO 52
POLÍGONOS E
QUADRILÁTEROS
B
b
C
a
c
A
d
D
C
B
D
A
E
B
C
A
E
D
X
B
C
γ
β
W
A
θ
α
Z
D
Y
B
A
C
D
B
C
A
D
B
A
C
D
B
C
A
D
B
A
C
D
B
A
C
D
B
A
C
D
B
A
C
D
B
M
A
C
N
D
B
C
M
A
N
D
Fixação
1) Qual o polígono convexo que tem 90 diagonais?
Fixação
F
2) A diferença entre o número de diagonais dos dois polígonos é 27 e o primeiro tem 3 lados3
a mais que o segundo. Determine os dois polígonos.
Fixação
3) Calcule a soma dos ângulos a, b, c, d, e, indicados na figura.
d
e
c
a
b
Fixação
4) O ângulo interno do polígono regular em que o número de diagonais excede de 3 o número
de lados é:
a) 60º
b) 72º
c) 108º
d) 150º
e) 120º
Fixação
^
5) Na figura, ABCD é um quadrado e CDEF é um losango. Se ECF mede 15º, a medida do
ângulo AÊF é:
E
a) 15º
b) 30º
c) 45º
d) 60º
D
A
e) 75º
15º
B
C
F
Fixação
F
6) Considere as seguintes proposições:
7
r
- todo quadrado é um losango;
- todo quadrado é um retângulo;
- todo retângulo é um paralelogramo;
- todo triângulo equilátero é isósceles.
Pode-se afirmar que:
a) só uma é verdadeira.
b) todas são verdadeiras.
c) só uma é falsa.
d) duas são verdadeiras e duas são falsas.
e) todas são falsas.
a
a
a
a
a
Fixação
7) (UFF) A figura abaixo representa o quadrado MNPQ de lado l = 4 cm. Sabendo que os
retângulos NXYZ e JKLQ são congruentes, o valor da medida do segmento YK é:
a) 3 cm
2
a) 2 3 cm
N
X
P
Y
Z
2 cm
a) 2 cm
2
1 cm
K
L I = 4 cm
a) 2 cm
a) 2 2 cm
M
J
Q
Fixação
8) (UERJ) Na análise dos problemas relativos
aos trapézios, aprende-se que é muito útil
traçar, por um dos vértices da base menor, um
segmento paralelo a um dos lados do trapézio.
Dessa forma, os trapézios podem ser estruturados como sendo a união de paralelogramos
e triângulos, conforme a ilustração a seguir.
centímetros que mais se aproxima da medidaF
da altura do trapézio é:
a) 3
9
B
b) 4
c
c) 5
a
d) 6
b
e) 7
c
d
T
c
U
b
S
e
a
b
T
R
c
U
C
a
(B - b)
P
S
R
Assim a análise de um trapézio RSTU
passa, basicamente para o triângulo de lados
a, c e b. A altura, a existência e os ângulos
do trapézio RSTU podem ser calculados a
partir dos correspondentes, no triângulo RSP.
Considere, então um trapézio onde as bases
medem 10 cm e 5 cm e os outros dois lados,
5 cm cada um. Logo, o número inteiro de
Fixação
9) (UNIFICADO) No quadrilátero ABCD da figura abaixo, são traçadas as bissetrizes CM e
BN, que formam entre si o ângulo α. A soma dos ângulos internos A e D, desse quadrilátero
corresponde a:
D
N
a) 3α
C
b) 2α
c) α
M
α
α
d)
2
A
α
e)
4
B
Proposto
1) A soma das medidas dos ângulos internos de um polígono regular é 2160º. Então o número de
diagonais deste polígono, que não passam pelo centro da circunferência que o circunscreve, é:
a) 50
b) 60
c) 70
d) 80
e) 90
Proposto
2) O ângulo interno de um polígono regular de 170 diagonais é igual a:
:a) 80º
b) 170º
c) 162º
d) 135º
e) 81º
Proposto
3) (UFRJ) De um retângulo de 18 cm de largura e 48 cm de comprimento foram retirados dois
quadrados de lados iguais a 7 cm, como mostra a figura. Qual o perímetro da figura resultante?
Proposto
4) (UERJ) Se um polígono tem todos os lados iguais, então todos os seus ângulos internos
são iguais.
Para mostrar que essa proposição é falsa, pode-se usar como exemplo a figura denominada:
a) losango;
b) trapézio;
c) retângulo;
d) quadrado.
Proposto
P
5) (FUVEST) O retângulo a seguir de dimensões a e b está decomposto em quadrados. Qual6
o valor da razão a/b?
a
a
a) 5/3
b) 2/3
c) 2
b
d) 3/2
e) 1/2
a
b
c
d
e
Proposto
6) (UNIRIO) No cubo a seguir, cada aresta mede 6 cm. Os pontos x e y são pontos médios das
arestas AB e GH. O polígono XCYE é um:
H
Y
F
E
D
A
X
G
C
B
a) quadrilátero, mas não é paralelogramo.
b) paralelogramo, mas não é losango.
c) losango, mas não é quadrado.
d) retângulo, mas não é quadrado.
e) quadrado.
Proposto
P
7) Num trapézio retângulo, a medida do maior ângulo interno é o quádruplo da medida do8
menor. A medida do menor dos ângulos desse trapézio é:
g
a) 30º
b) 36º
c) 45º
d) 72º
e) 90º
Proposto
8) Na figura seguinte, ABCD é um quadrado e BCE é um triângulo equilátero. Calcular, em
graus, a medida do ângulo BFD.
D
C
E
A
B
Proposto
9) (UFRJ) Na figura a seguir, A não pertence ao plano determinado pelos pontos B, C e D. Os
pontos E, F, G e H são os pontos médios dos segmentos AB, BC, CD e DA, respectivamente.
A
E
B
H
D
F
C
G
Prove que EFGH é um paralelogramo.