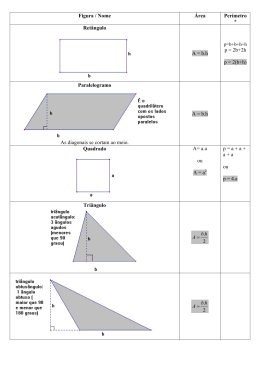
Comprimentos e Áreas
Introdução
Desde os egípcios, que procuravam medir e demarcar suas terras, até hoje,
quando topógrafos, geólogos e arquitetos fazem seus mapeamentos e plantas,
o cálculo de áreas tem sido uma preocupação constante.
Nesta aula você aprenderá como resolver problemas envolvendo áreas.
Área do Retângulo
Tomando como unidade de área o quadrado de 1cm², observamos que cabem
12 desses quadrados no retângulo ao lado. Logo, a área do retângulo é 12cm².
Figura 1
Por outro lado, se multiplicarmos a medida do comprimento do retângulo pela
medida da sua largura, obtemos o mesmo resultado.
Figura 2
Portanto, a área da superfície de um retângulo é igual ao produto das medidas
da base e da altura .
82
Figura 3
Onde
e
são números reais positivos.
Área do quadrado
Particularmente, para o quadrado de lado , ou seja,
e
, temos:
Figura 4
Onde “ ” é um número real positivo.
Área do paralelogramo
Cortando um pedaço do paralelogramo, podemos encaixá-lo do outro lado,
transformando-o num retângulo. Veja:
𝑏
Figura 5
83
𝑏
Figura 6
Então, podemos definir que a área do paralelogramo é igual à área do
retângulo:
𝐴𝑝𝑎𝑟𝑎𝑙
Em que
e
𝑏.
*+
Área do triângulo
Toda região triangular é metade da região limitada por um paralelogramo de
mesma base e altura.
Como dividimos um paralelogramo em dois triângulos iguais, a área de cada
um dos triângulos é igual à metade da área do paralelogramo:
Figura 6
Área do Trapézio
Trapézio é todo quadrilátero com apenas um par de lados paralelos, que são
suas bases. Como pode ser visto na Figura 7.
Figura 7
84
Vamos decompor a região limitada por um trapézio para encontrar sua área.
Considere um trapézio de bases ,
e altura
(números reais positivos).
Primeiro, decompomos a região traçando uma de suas diagonais.
Figura 8
Observe que temos agora duas regiões triangulares:
𝑎
𝑎
𝐵
𝑏
Figura 10
Figura 9
A área de uma região triangular nós já aprendemos a calcular, então temos:
A T  A1  A 2
b.a
B.a

2
2
b.a  B.a

2
(b  B ).a

2
AT 
AT
AT
Ou seja:
85
𝐴 𝑇𝑟𝑎𝑝
𝑏+𝑏 .𝑎
2
Área de um losango
Todo losango pode ser transformado num retângulo equivalente, com altura
e base .
2
Assim, a área da região limitada por um
losango é dada pela metade do produto
das medidas das diagonais.
𝐴𝑙𝑜𝑠𝑎𝑛𝑔𝑜
𝐷. 𝑑
2
Figura 12
Área de um hexágono regular
Um hexágono regular é formado por seis regiões triangulares equiláteras.
Como a área de uma região triangular equilátera é dada por:
.√
,
A área do hexágono é dada por:
A hexágono  6 
l ² 3 6l ² 3

4
4
Simplificando esta equação, tem-se que:
𝐴ℎ𝑒𝑥
𝑔𝑜𝑛𝑜
Em que é um número real positivo.
86
3𝑙 2 √3
2
Área de um Polígono Retangular
Um polígono regular é aquele que tem todos os lados e todos os ângulos
internos congruentes. Ele pode sempre ser inscrito em uma circunferência.
Figura X
Pode-se perceber que se o polígono regular tem lados, a região limitada por
ele pode ser decomposta em regiões limitadas por triângulos isósceles.
Em cada um desses triângulos, a base é o lado ( ) e a altura é o apótema ( ). Logo,
𝐴𝑝𝑜𝑙í𝑔𝑜𝑛𝑜 𝑟𝑒𝑔.
Em que
𝑙. 𝑎
𝑛.
2
: lado
: apótema
: número de lados
Todas estas variáveis representam valores reais positivos.
REFERÊNCIAS BIBLIOGRÁFICAS
BONJORNO, J. R.; BONJORNO, R. A.; OLIVARES, Ayrton. Matemática:
Fazendo a diferença. São Paulo: FTD, 2006.
DANTE, L. R. Matemática. Vol. Único. São Paulo: Ática, 2005.
.
87