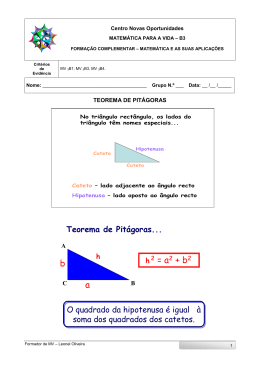
Lista 2: Vetores - Licenciatura em Matemática
Professora: Ivanete Zuchi Siple
1. Mostre que os pontos médios dos lados de um quadrilátero são os vértices de um paralelogramo.
2. Dois vetores são perpendiculares se, e somente se, o seu produto interno é igual a zero.
3. Prove que o segmento que une os pontos médios de dois lados de um triângulo é paralelo ao
terceiro e tem a metade de sua medida.
4. Prove que as diagonais de um losango são ortogonais entre si.
5. No triângulo retângulo abaixo, demonstre vetorialmente as seguintes relações:
(a) O quadrado de um cateto é igual ao produto da hipotenusa pela projeção desse cateto sobre
a hipotenusa, ou seja b2 = an e c2 = am.
(b) O quadrado da altura é igual ao produto das projeções dos catetos sobre a hipotenusa, ou
seja, h2 = mn
6. Demonstre vetorialmente a lei dos senos num triângulo qualquer.
7. Considere o triangulo ABC e sejam M o ponto medio de BC, N o ponto medio de AC e P o ponto
medio de AB. Mostre que as medianas se cortam num mesmo ponto que divide as medianas na
proporçâo 32 e 13 .
8. Mostre, usando vetores, que o ponto médio M de um segmento que une os pontos A(x1 , y1 ) e
2 y1 +y2 z1 +z2
, 2 , 2 ).
B(x2 , y2 ) é M = ( x1 +x
2
1