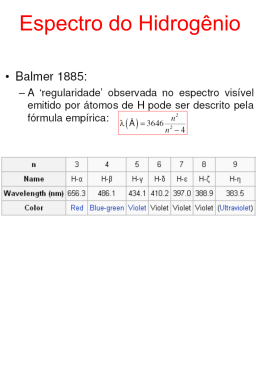
O Modelo Atômico de Bohr A estrutura do átomo revelada. O Espectro Atômico Radiação Contínua Hidrogênio Hélio Mercúrio O Espectro Atômico A assinatura do átomo Produção e observação do espectro: Descarga elétrica passa através de gás monoatômico contido em um tubo. Colisões com elétrons e mesmo entre si levam os átomos a energias mais altas. Ao retornarem para o estado normal os átomos liberam esse excesso de energia na forma de radiação eletromagnética. Ao passar por uma rede de difração (ou prisma) o espectro é separado em seus comprimentos de onda e registrado em uma placa fotográfica para medição. A natureza do espectro atômico: Ao contrário do espectro contínuo emitido por corpos sólidos a altas temperaturas, o espectro atômico revela-se como um conjunto discreto de comprimentos de onda. Emissão característica: Átomos de diferentes elementos revelam espectros discretos específicos. Informação de grande importância prática na identificação atômica. Contudo apresenta em geral grande complexidade com espectros de centenas de linhas. O átomo de Hidrogênio A Série de Balmer n2 0 2 n 4 O espectro atômico do Hidrogênio O espectro do H é o mais simples. Parte do espectro característico do H se localiza na região do visível. Observa-se que os ’s diminuem em separações cada vez menores, indicando uma série que converge para um valor limite 0= 364,56 nm. J. Balmer (1885) estabeleceu empiricamente a fórmula que reproduz os valores da série de linhas para n= 3, 4, 5 ... A fórmula de Rydberg J.R. Rydberg (1890) desenvolveu uma forma mais conveniente de expressar as séries em termos do recíproco do comprimento de onda ( = 1/) Para a série de Balmer: 1 1 RH 2 2 2 n 1 RH= (10.967.757 1) m-1 (por medidas espectroscópicas) O Átomo de Bohr Modelo para o átomo de um elétron Os postulados de Bohr (1913) 1. 2. 3. 4. O elétron orbita o núcleo em movimento circular sob a ação da força coulombiana conforme as leis da mecânica clássica. Só é possível ao elétron mover-se em órbitas para as quais o seu momento angular seja múltiplo inteiro de ћ (h/2). Apesar do elétron estar constantemente acelerado, ele não irradia.energia eletromagnética na órbita permitida . Radiação eletromagnética só é liberada quando o elétron “salta” de forma descontínua de uma órbita com energia Ei para outra com energia Ef, tal que a frequência da radiação emitida é dada por: = (Ei – Ef)/h. Desenvolvimento do modelo Núcleo: carga +Ze e massa M Elétron: carga –e e massa m (m << M) em órbita circular de raio r. Fc= mv2/r = (1/40).Ze2/r2 L= mvr= cte. Quantização: L= n.ћ (n= 1, 2, 3 ...) Raio e velocidade das órbitas n 2 2 r 4 0 m Ze2 Ze2 v 4 0 n 1 Energia total E= U + K Ze 2 U 4 0 r Ze 2 K 8 0 r A solução de Bohr Átomo nuclear estável e espectro explicados Níveis discretos de energia m Z2 e 4 1 En (4 0 ) 2 2 2 n 2 O Espectro atômico discreto Salto quântico do nível ni nf 1 c E E i f hc k 1 m Z2 e 4 1 1 4 4 3c n 2 n 2 0 i f 2 1 1 R Z 2 2 2 n f ni 1 Constante de Rydberg calculada pelo modelo para o H, com os valores conhecidos das constantes universais: me4 R 2 3 1,096897107 m 8 0 h c A solução de Bohr A precisão do modelo para o átomo de Hidrogênio Núcleo de massa finita Até para o H (M 2000.m), a aproximação M é bastante razoável. Contudo pode-se adotar a correção de massa finita do núcleo com (M 1836.m), substituindo o valor da massa do elétron pela sua massa reduzida nas equações: m.M/(m+M) A Cte. de Rydberg corrigida: RM R./m= 10.968.100 m-1 Valor que concorda com dados de medidas espectroscópicas em cerca de 3 partes por 100.000! RH= (10.967.757 1) m-1 Como apresentado antes. O caso do Deutério (D) Isótopo do H com 1 neutron: MD 2M Produz um deslocamento das linhas () do espectro para valores ligeiramente menores. Linha H (vermelha) da série de Balmer para D: O Experimento de Franck-Hertz Comprovação independente dos estados quantizados de energia do átomo J. Franck e G. Hertz (1914) Tradução comentada - Copyright © Michael Richmond Simulação do Experimneto de FranckHertz Generalização das Regras de Quantização Casos particulares Planck: E= nh Bohr: L= nћ • Caso do OHS unidimensional Partícula submetida a uma força tipo: F= -kx Energia total: px2 k .x 2 E 2m 2 Regras de Wilson e Sommerfeld (1916) Para todo sistema físico, cujas coordenadas sejam funções periódicas do tempo, a condição de quantização de cada coordenada ser tal que: p dq n h q E= K + V Neste caso: e como px dx 2E nh k m k m 2 q Sendo q a coordenada em questão e pq o momento associado a q. Integração sobre um ciclo da coordenada. Temos finalmente: E nh Reproduzindo a Lei de quantização de Planck. Generalização das Regras de Quantização • Caso da partícula em órbita circular Elétron atômico em órbita de raio r. Momento angular: L= mvr= cte. p dq Ld Neste caso: • Interpretação de de Broglie (1924) Para a regra de quantização de Bohr. L= mvr = pr = nh/2π mas, p= h/λB q então: 2πr= nλB (n= 1, 2, 3 ...) Assim: 2 L d 2L nh 0 Temos finalmente: Ln h 2 Reproduzindo a lei de quantização de Bohr. As órbitas permitidas, aos elétrons atômicos, são aquelas para as quais a circunferência contém, exatamente um número inteiro de comprimentos de onda de de Broglie. As ondas de de Broglie e as órbitas de Bohr O Modelo de Sommerfeld A estrutura fina do átomo de hidrogênio Órbitas elípticas Semi-eixo maior: a Semi-eixo menor: b Distância entre focos: F1-F2= 2c Excentricidade: e= c/a Regras de Quantização Ld n h L n (n 1,2,3...) p dr n h L(a / b 1) n (n r r r r 0,1,2,3...) E uma 3ª equação p/força centrípeta. O Modelo de Sommerfeld A estrutura fina do átomo de hidrogênio A solução de Sommerfeld Forma e tamanho das órbitas: n n 2 2 a 4 0 b a 2 Ze n Números quânticos: n= nθ + nr nθ= 1, 2, 3 ...n (principal) (azimutal) Energia total: Z 2e4 1 E 40 2 2 2n2 Estados degenerados de energia (mesmo n). Ou seja, mesma energia para diferentes órbitas com mesmo nº quântico principal. O Modelo de Sommerfeld Removendo a degenerescência Correção relativísticas da me A estrutura fina do hidrogênio Cálculo de Bohr mostrou que: v/c ≈ 10-2 produz correções de ≈ (v/c)2 em me e E Que é da ordem (10-4) de separação das linhas de estrutura fina, observadas no espectro do hidrogênio! Velocidade média dos elétrons Dependerá da elipcidade da órbita (nθ) Recalculando a Energia total: Z e 1 Z E 1 n 4 0 2 2 2 n 2 2 4 2 2 1 3 n 4n e2 1 7,297103 Onde, 4 0 c 137 1 É a constante de estrutura fina. As transições observadas são representadas pelas setas de linha cheia. Transições permitidas são definidas pela seguinte regra de seleção: nθi – nθf = 1 O Princípio da Correspondência Uma justificativa para as regras de seleção Enunciado de Bohr (1923) 1. 2. As previsões da teoria quântica para o comportamento de qualquer sistema físico deve corresponder às previsões da física clássica no limite em que os números quânticos que especificam o estado do sistema se tornem muito, muito grandes. Uma regra de seleção deve ser verdadeira para toda a faixa do número quântico considerado. Assim, qualquer regras que sejam necessárias para obter a correspondência no limite clássico (n grande) se aplica igualmente no limite quântico (n pequeno).
Baixar