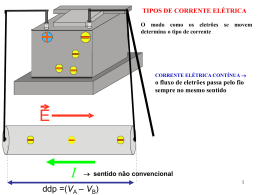
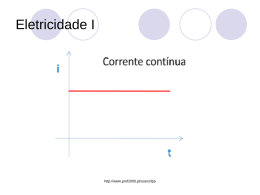
Análise de Circuitos
em Corrente Alternada
Tensão Contínua
Tensão continua ou constante pois o seu
valor não se altera com o tempo.
comportamento da tensão nos terminais da bateria
ao longo do tempo: A tensão não muda, permanece
constante.
Tensão Alternada
O seu valor e polaridade
longo do tempo.
se modificam ao
Conforme o comportamento da tensão então
temos os diferentes tipos de tensão alternada:
senoidal, quadrada, triangular, pulsante,
etc.
De todas essas a senoidal é a que tem um
maior interesse pois é a senoidal a tensão
que é gerada nas usinas e que alimenta as
industrias e residências.
Considerando o circuito da figura abaixo, no qual
temos duas baterias e uma chave que ora conecta
a bateria B1 ao resistor, ora conecta a bateria B2 ao
resistor. Vamos supor que cada bateria fica
conectada ao resistor durante 1s. Como seria o
gráfico da tensão em função do tempo nos
terminais da bateria ?
Tensão Senoidal
A grande vantagem da alimentação em AC,
comparativamente à DC onde as grandezas têm uma
evolução constante no tempo, verifica-se na eficiência do
transporte de energia por esta se poder fazer a muito alta
tensão; a tensão alternada produzida numa central é
elevada por um transformador que, conseqüentemente
diminui, aproximadamente, na mesma proporção a
corrente; as perdas são assim menores em alta tensão, do
que seriam se a energia fosse transportada ao nível de
tensão a que é produzida. Esta foi a principal razão porque
os sistemas AC se impuseram face aos sistemas DC.
Tensão Senoidal
É uma tensão que varia com o tempo de acordo com uma
lei senoidal, portanto nesse caso temos uma expressão
matemática para expressar a tensão (no caso da tensão
quadrada não temos). A expressão matemática é:
v(t)= VM.sen(wt + o) ou
v()
= VM.sen 
Onde VM (em V) é o valor de pico (valor máximo que a
tensão pode ter), w em (rd/s) é a freqüência angular e 0
(rd ou graus) é o angulo de fase inicial,  é o ângulo num
determinado instante t.
Observe que a relação entre ângulo e tempo é dada por :
 = 0 +w.t
Tensão Senoidal
A freqüência angular relaciona-se com a freqüência,
expressa em ciclos por segundo ou hertz (Hz), através
de:
=2f
A freqüência pode ser expressa em função do período,
através de:
f= 1/T
Todos estes parâmetros da senóide estão graficamente
representados na figura seguinte
Todos estes parâmetros da sinusóide estão
graficamente representados na figura seguinte
Então uma tensão senoidal varia em função do
tempo de acordo com uma lei senoidal, mas a
mesma tensão pode ser representada em função
do ângulo (não esqueça que a função seno tem
período de 360 graus ou de 2 rd), sendo a
relação entre ângulo e tempo dada por = 0 +w.t
Dadas duas grandezas sinusoidais com igual frequência, descritas
pelas expressões:
designa-se por desfasagem entre as grandezas, a diferença de fases
iniciais,
.
De acordo com o exemplo dado, diz-se que a grandeza x(t) está
avançada
radianos, relativamente a y(t).
Valor Eficaz
O conceito de valor eficaz de uma tensão ou corrente
alternada senoidal está diretamente ligado à potência
transferida por esse par de grandezas; é através do valor
eficaz que se pode comparar a potência associada a
grandezas AC com potências associadas a grandezas DC.
Fisicamente , o valor eficaz de uma corrente alternada é
o valor da intensidade de uma corrente contínua que
produziria, numa resistência, o mesmo efeito calorífico
que a corrente alternada em questão.
Matematicamente, o valor eficaz, Xef, de uma grandeza
periódica x(t) é determinado através de:
O caso particular de uma grandeza alternada senoidal
expressa por
, que conduz a:
Poder-se-á assim escrever:
Graficamente, o valor eficaz está relacionado com a
área sob a curva que representa a evolução temporal do
quadrado da grandeza, tal como se representa na figura
seguinte.
O valor eficaz de uma grandeza altera-se com a
amplitude, com perturbações na forma da onda, mas
não é afetado por variação da freqüência, nem da fase
inicial
P. ex. uma tensão senoidal de 155V de pico é
aplicada a uma resistência de 100 Ohms. Se ao
mesmo resistor for aplicado uma tensão de 110V
contínuos, a dissipação de potência será a mesma.
Para a tensão senoidal representada abaixo
determine os seus parâmetros: VP=VM= ______V,
VPP= _____V, VRMS= ____V, T= ____ms, f= ____Hz,
w = ____ rd/s e 0 = ____
Representar as seguintes tensões senoidais
v1(t) = 15.sen(2. .103.t ) ( V ).
v2(t) = 20.sen(2. .103.t + /2 )( V ).
NOTAÇÃO COMPLEXA
É uma forma de representar grandezas alternadas
senoidais através de vetores que variam no tempo
(vetores girantes). A notação complexa foi introduzida
por Steinmetz, em 1893, e veio simplificar a análise do
regime permanente de circuitos alimentados em AC.
Pretende-se determinar qual o vetor representativo da
tensão descrita por
Partindo da função de Euler
onde
j
presenta a unidade imaginária, pode-se escrever:
multiplicando
ambos
os
membros da expressão por UM, obtém-se:
que será designado
por vetor girante e representado por:
NOTAÇÃO COMPLEXA
Comparando a expressão de com
a da evolução
temporal de u(t), conclui-se que u(t) corresponde à
parte imaginária de
. Em termos matemáticos
tem-se:
Atendendo a que
o número complexo
pode ser representado no plano complexo como um
vetor que, para t=0, vale
e que rodará com
freqüência angular  ao longo do tempo
(correspondente à multiplicação por
)
NOTAÇÃO COMPLEXA
Representação gráfica de um vetor
girante
O vetor
designa-se por amplitude complexa de
. Graficamente, a tensão descrita por
será, em cada instante, a projeção de
sobre o eixo
dos imaginários.
Diagrama Fasorial
Circuitos Resistivos em CA
Em um circuito puramente resistivo alimentado por uma
tensão alternada (CA), a tensão e a corrente estão em
fase, sendo a relação entre elas dada pela lei de ohm,
isto é : V =R.I ou I = V/R, sendo que usamos valores
eficazes para I e V. Em termos de diagrama fasorial
significa que os fasores representativos da tensão e da
corrente estão em fase.
Indutor
Chamamos de indutor a um fio enrolado em forma de
hélice em cima de um núcleo que pode ser de ar ou de
outro material. A figura abaixo mostra o símbolo para
indutor com núcleo de ar, de ferro e de ferrite.
Indutor em Corrente Contínua
O que acontece quando no circuito da figura abaixo quando
fechamos a chave? A tensão é aplicada no indutor mas a
corrente leva um certo tempo para crescer, a explicação é um
fenômeno chamado auto indução. Ao abrir a chave, no instante
t2, novamente esse fenômeno vai atuar na bobina não deixando
a corrente se anular instantaneamente.
Indutor em Corrente Alternada Senoidal
A corrente em um indutor está atrasada em relação à
tensão em um circuito CC. O que acontece se
alimentarmos um indutor ideal de indutância L com uma
tensão alternada senoidal de freqüência f?
A corrente continua atrasada em relação à tensão e
agora de um ângulo bem definido, 90º.
Concluímos que um indutor se opõe à passagem de uma
corrente alternada (se opõe à variação de uma corrente)
e que a corrente está atrasada em relação à tensão.
Caso o núcleo fosse de ferro ou ferrite a corrente
demoraria mais para aumenta (ou diminuir), isto porque a
indutância da bobina seria diferente em cada caso. A
indutância (L) de um indutor é um parâmetro que dá a
medida da capacidade que tem o indutor de armazenar
energia no campo magnético, a sua unidade se chama
Henry (H).
Quanto maior a indutância (L) mais tempo levará para que
a corrente no gráfico atinja o seu valor máximo. O valor da
indutância depende do número de espiras e do material
usado no núcleo.
Reatância Indutiva
Como vimos um indutor se opõe à variação de
uma corrente. A medida desta oposição é dada
pela sua reatância indutiva ( XL ), sendo calculada
por:
Com L especificado em Henrys
hertz (Hz), XL em ohms (  ).
(H),
f
em
Capacitor em corrente alternada senoidal
Quando ligamos um capacitor em um circuito CC,
inicialmente a corrente é máxima com tensão nula no
capacitor, isto é, existe uma defasagem entre a corrente e
a tensão. Se um capacitor ideal (não tem resistência de
perdas) for ligado à uma tensão alternada senoidal, a
corrente estará 90º adiantada em relação à tensão.
Reatância Capacitiva
É a medida da oposição oferecida pelo capacitor à
passagem da corrente alternada é calculada por:
com C em Farads (F), f em Hertz (Hz) resultando
XC em Ohms (W).
Para calcularmos o módulo da corrente no circuito
poderemos usar a lei de Ohm, isto é :
Impedância Complexa
Impedância Complexa
Define-se impedância complexa, Z a razão entre os
vetores girantes da tensão e da corrente:
Explicitando a impedância complexa de cada um
dos elementos R, L e C, obtém-se:
Uma impedância complexa expressa-se em Ohm 
Impedância Complexa
Pode-se representar vetorialmente as impedâncias e
as amplitudes complexas de cada um dos elementos.
Note-se que a impedância não é um vetor girante, pois
não está a representar qualquer grandeza alternada
senoidal.
Saliente-se, também, o fato de as impedâncias das
indutâncias e dos capacitores se alterar com a
freqüência de alimentação do circuito, contrariamente
ao que acontece com a impedância da resistência
CIRCUITO RL SÉRIE
Na prática um indutor apresenta uma resistência, e além disso
podemos ter resistores em série com o indutor, neste caso a corrente
continuará atrasada em relação à tensão mas de um angulo menor
do que 90º. A figura mostra o circuito e o diagrama fasorial, com as
seguintes expressões:
circuito RL série
Exercício 1: Para o circuito pede-se determinar:
a) Impedância, b) corrente, tensão em R e em L, c) cosf
e d) Formas de onda da tensão total e da corrente
CIRCUITO RC SÉRIE
Relembrando, em um circuito puramente resistivo a
tensão e a corrente estão em fase, e num circuito
puramente capacitivo a corrente esta 90º adiantada em
relação à tensão. Num circuito como o da figura abaixo a
corrente continua na frente da tensão mas de um angulo
menor do que 90º. Observe o seu diagrama fasorial
resultante.
circuito RC série
Define-se a impedância (Z) do circuito como sendo: Z=V/ I
A impedância é a soma dos efeitos da resistência (R=VR/ I) e da
reatância capacitiva (XC=VC/ I) na oposição à passagem da corrente.
O diagrama fasorial nos mostra o seguinte:
1- f é o angulo de defasagem entre a tensão total
e a corrente consumida pelo circuito (I).
2- A corrente no capacitor continua adiantada
em relação à tensão no capacitor (VC).
3- A corrente na resistência (I) está em fase com a tensão na
resistência(VR) e defasada de 90º em relação à tensão no capacitor(VC).
A tensão total do circuito é obtida somando VR com VC vetorialmente.
Do diagrama fasorial obtemos as relações básicas deste circuito:
circuito RC série
Se dividirmos por I2 a primeira igualdade obteremos
expressão que calcula a impedância do circuito
a
O angulo de defasagem, f, também pode ser calculado a partir do
diagrama fasorial sendo dado por:
cos f= R / Z
logo
f= arcos(R/Z)
CIRCUITO RC PARALELO
As mesmas considerações feita para o circuito RC série vale
para o RC paralelo, ou seja, em um circuito puramente
resistivo a tensão e a corrente estão em fase, e num
circuito puramente capacitivo
a corrente
esta 90º
adiantada em relação à tensão.
circuito RC paralelo
Para este circuito valem as expressões
CIRCUITO RL PARALELO
No circuito abaixo temos o circuito e o diagrama fasorial
de um circuito RL paralelo. A corrente total se divide
entre o indutor e o resistor e continuam válidas as
características do indutor ideal (corrente atrasada de 90º
em relação à tensão).
circuito RL paralelo
É importante notar que a fase inicial da tensão do gerador é
ARBITRÁRIA.Caso tivéssemos considerado a fase inicial de V igual
a 0º, todo desenho deveria ser deslocado de 90º no sentido horário.
Cálculo da Impedância
Do ponto de vista de análise, não interessa
saber qual a fase inicial da tensão da rede. O
que importa realmente é a defasagem entre a
tensão total (tensão da rede) e a corrente total
(corrente fornecida pela rede), e o que
determinará essa defasagem será a carga (R e
L). Para este circuito valem as seguintes
expressões.
Z= R.XL/(R2+XL2)0.5
CIRCUITO RLC SÉRIE - RESSONÂNCIA
Para analisar o circuito abaixo deveremos lembrar que a
tensão total aplicada é a soma vetorial das tensões VC, VR e
VL. No diagrama fasorial a tensão na resistência está em
fase com a corrente, a tensão na indutância está adiantada
de 90º enquanto a tensão no capacitor está atrasada de 90º
circuito rlc série - ressonância
No diagrama fasorial estamos considerando, arbitrariamente,
que o circuito é indutivo, e portanto VL > VC, e desta forma
a corrente estará atrasada em relação à tensão. Para obter a
expressão da tensão total e da impedância devemos fazer a
soma vetorial das três tensões.
Observe que VL e VC tem mesma direção mas sentidos
oposto, logo a resultante da operação VL - VC terá o sentido
de VL.
circuito rlc série - ressonância
Impedância e Ressonância
Para o circuito anterior vale as seguintes expressões:
Da equação que se obtém o calculo da impedância observamos
que se XL= XC a impedância será igual a R, isto é, o circuito
será puramente resistivo e a corrente estará em fase com a
tensão. Esta situação é conhecida como ressonância, e ocorre
numa freqüência f0 calculada por :
circuito rlc série - ressonância
O circuito ressonante tem as seguintes características:
•Na freqüência de ressonância, o circuito é puramente resistivo, sendo
a corrente máxima de valor V/R, estando em fase com a tensão.
•Abaixo da freqüência de ressonância a impedância será capacitiva
(XC > XL), estando a corrente adiantada em relação à tensão.
•Acima da freqüência de ressonância a impedância será indutiva (XC
< XL), estando a corrente atrasada em relação à tensão.
CIRCUITO RLC PARALELO - RESSONÂNCIA
Como sabemos, num circuito paralelo a tensão é a mesma
em todos os elementos, veja o circuito RLC paralelo e o
diagrama fasorial com a representação das três correntes e
da tensão total.
circuito rlc paralelo - ressonância
Considerando que IL >IC então obtemos o diagrama fasorial
final onde representamos a soma vetorial das três
correntes(IL, IC e IR).
circuito rlc paralelo - ressonância
Para este circuito são válidas as expressões :
Ressonância
Se XL = XC na expressão da impedância obteremos Z = R,
isto é, o circuito será puramente resistivo sendo esta situação
chamada de ressonância e isso ocorre na freqüência f0 dada
por:
O circuito ressonante tem as seguintes características :
•Na freqüência de ressonância f0, o circuito é puramente
resistivo, sendo a corrente mínima de valor V/R, estando em fase
com a tensão.
•Abaixo da freqüência de ressonância a impedância será indutiva
(XC < XL ), estando a corrente atrasada em relação à tensão.
•Acima da freqüência de ressonância a impedância será capacitiva
( XC > XL ), estando a corrente adiantada em relação à tensão.
Referências
http://www.lei.ucl.ac.be/multimedia/eLEE/PO/realisations/CircuitsElectri
ques/index.htm
http://www.dt.fee.unicamp.br/~www/ea513/ea513.html
http://www.if.ufrgs.br/tex/fis142/