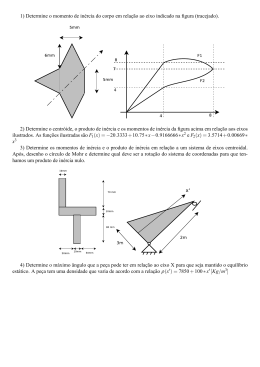
1
Engenharia da Computação
4º / 5° Semestre
RESISTÊNCIA DOS MATERIAIS – AULAS 01
Prof Daniel Hasse
Características Geométricas de Figuras Planas
SÃO JOSÉ DOS CAMPOS, SP
Aula 01 – Figuras Planas I
1- FIGURAS PLANAS
Nesta aula iremos estudar as principais características geométricas das figuras, como por exemplo, área,
momento estático e centróide.
1.1 – Área
O conceito de área já é conhecido de disciplinas anteriores, podemos generalizar o cálculo da área como
sendo a integral definida de um elemento de área 𝑑𝐴 em um domínio 𝐴.
𝐴 = � 𝑑𝐴
𝐴
1.1.1 – Propriedades da área
•
•
•
As unidades de área possuem a forma 𝐿2 , como por exemplo, 𝑚 2, 𝑘𝑚 2 , 𝑚𝑚2 e 𝑝𝑜𝑙2 ;
São sempre positivas;
São aditivas, podem-se somar áreas diferentes desde que possuam a mesma unidade, como se
pode observar na figura a seguir:
𝐴 𝑇 = 𝐴1 + 𝐴2 + 𝐴3
1.2 – Momento Estático com relação a um eixo
Ao contrário da área, o momento estático é sempre relacionado a um eixo. Tomamos o elemento de área
infinitesimal 𝑑𝐴 e multiplicamos pela distância a este eixo e fazemos a integral em todo domínio 𝐴.
De modo geral estamos mais interessados com relação aos momentos estáticos com relação aos eixos de
coordenadas, como visto abaixo.
Momento estático com relação ao eixo X
𝑀𝑆𝑥 = � 𝑦𝑑𝐴
𝐴
Momento estático com relação ao eixo Y
𝑀𝑆𝑦 = � 𝑥𝑑𝐴
𝐴
1
Aula 01 – Figuras Planas I
1.2.1 – Propriedades do Momento Estático
•
•
•
As unidades de momento estático possuem a forma 𝐿3 , como por exemplo, 𝑚 3, 𝑘𝑚 3 , 𝑚𝑚3 e 𝑝𝑜𝑙3 ;
Pode ser positivo, negativo ou nulo, dependendo das coordenadas envolvidas (coordenadas
positivas momento estático positivo, coordenadas negativas momento estático negativo,
coordenadas simétricas momento estático nulo);
É aditivo, podem-se somar momentos estáticos diferentes desde que possuam o mesmo eixo de
referência, como se pode observar na figura a seguir:
𝑀𝑆𝑥 = 𝑀𝑆𝑥 1 + 𝑀𝑆𝑥 2 + 𝑀𝑆𝑥 3
1.3 – Centróide ou Centro de Gravidade
Defini-se como Centróide ou Centro de Gravidade o ponto onde se pode concentrar toda a área de uma
figura, sendo possível assim definir o momento estático como sendo o produto da área pela distância deste
ponto ao eixo a que se refere o momento estático.
𝑀𝑆𝑥 = � 𝑦𝑑𝐴 = 𝐴𝑦𝐺
𝐴
𝑀𝑆𝑦 = � 𝑥𝑑𝐴 = 𝐴𝑥𝐺
𝐴
Deste modo as coordenadas do centro de gravidade podem ser
calculadas por:
𝑥𝐺 =
𝑀𝑆𝑦 ∫𝐴 𝑥𝑑𝐴
=
𝐴
𝐴
𝑦𝐺 =
𝑀𝑆𝑥 ∫𝐴 𝑦𝑑𝐴
=
𝐴
𝐴
Utilizando estas expressões podemos calcular a posição do centro de gravidade de figuras elementares.
Estes valores normalmente são encontrados em tabelas, como a que se encontra ao final desta aula no
Apêndice A.
Nota: O momento estático tomado com relação a qualquer eixo que passa pelo centro de gravidade da
figura é nulo e se o momento estático for nulo, o eixo passa pelo centro de gravidade da figura.
2
Aula 01 – Figuras Planas I
Exemplo Resolvido: Cálculo das propriedades geométricas de um retângulo
Cálculo da Área
y
𝑑𝐴 = 𝑏𝑑𝑦
ℎ
𝐴 = � 𝑑𝐴 = � 𝑏𝑑𝑦
𝐴
h
0
ℎ
𝐴 = 𝑏𝑦| = 𝑏ℎ
0
Cálculo do Momento Estático
dy
𝑀𝑆𝑥
x
𝑀𝑆𝑦
b
Cálculo do Centróide ou Centro de Gravidade
ℎ
ℎ
𝑏
𝑏
𝑏𝑦 2
𝑏ℎ 2
� =
= � 𝑦𝑑𝐴 = � 𝑦𝑏𝑑𝑦 =
2 0
2
𝐴
0
ℎ𝑥 2
ℎ𝑏2
� =
= � 𝑥𝑑𝐴 = � 𝑥ℎ𝑑𝑥 =
2 0
2
𝐴
0
ℎ𝑏2
𝑀𝑆𝑦
𝑏
= 2 =
𝑥𝐺 =
𝐴
𝑏ℎ
2
𝑏ℎ 2
𝑀𝑆𝑥
ℎ
𝑦𝐺 =
= 2 =
𝐴
𝑏ℎ
2
1.4 – Método Prático para a determinação das propriedades geométricas
Na maioria das vezes quando lidamos com figuras com formas complicadas torna-se difícil definir uma
função matemática que descreva esta figura, como é o exemplo da figura a seguir:
Nesses casos utilizamos um método prático, baseado nas propriedades aditivas da área e momentos
estáticos, este método consiste em dividir a figura em figuras menores com propriedades conhecidas,
nesse exemplo iremos dividir a figura em três outras figuras menores, um retângulo, um semicírculo e um
triângulo.
3
Aula 01 – Figuras Planas I
O método prático consiste em montar uma tabela contendo todas as informações de cada uma das figuras
resultantes da subdivisão, apenas neste caso utilizaremos valores negativos para área, porém, temos que
ter em mente que isto é um artifício para se descontar da figura original uma área sem material, esta tabela
encontra-se a seguir e para todos os casos a serem estudados possuirá as mesmas colunas alterando-se
apenas as linhas de acordo com a figura original.
Figura
𝑨𝒊
𝑨𝒚𝑮𝒊
4,67
𝒚𝑮𝒊
𝑨𝒙𝑮𝒊
3
𝒙𝑮𝒊
1
14
3
-3,53
2,5
0,64
-8,83
-2,26
11,47
---
---
29,17
18,74
12
∑
2
1,5
24
18
Para se determinar o centróide ou centro de massa basta dividir o somatório do produto 𝐴𝑥𝐺𝑖 e 𝐴𝑦𝐺𝑖 pelo
somatório de área, assim temos:
𝑥𝐺 =
𝑦𝐺 =
∑ 𝐴𝑥𝐺𝑖 29,17
=
= 2,54
∑𝐴
11,47
∑ 𝐴𝑦𝐺𝑖 18,74
=
= 1,63
∑𝐴
11,47
4
Aula 01 – Figuras Planas I
APÊNDICE A – FORMULÁRIO DE PROPRIEDADES GEOMÉTRICAS DAS FIGURAS MAIS COMUNS
5
Aula 01 – Figuras Planas I
6
Aula 02 – Figuras Planas II
1- FIGURAS PLANAS
Nesta aula iremos continuar a estudar as principais características geométricas das figuras, como por
exemplo, momento de inércia, momento polar de inércia e raio de giração.
1.1 – Momento de Inércia com relação a um eixo
Assim como o momento estático já estudado na aula anterior, o momento de inércia também é sempre
relacionado a um eixo de referência. Tomamos o elemento de área infinitesimal 𝑑𝐴 e multiplicamos pelo
quadrado da distância a este eixo e fazemos a integral em todo domínio 𝐴.
Para os eixos cartesianos, os momentos de inércia podem ser definidos pelas seguintes integrais:
Momento de inércia com relação ao eixo X
𝐼𝑥 = � 𝑦 2 𝑑𝐴
𝐴
Momento de inércia com relação ao eixo Y
𝐼𝑦 = � 𝑥 2 𝑑𝐴
𝐴
1.1.1 – Propriedades do Momento de Inércia
•
•
•
•
Normalmente a notação utilizada para representar o momento de inércia é a letra 𝐼, porém, em
algumas bibliografias a letra 𝐽 também é utilizada, mas esta última normalmente refere-se ao
momento de inércia de massa, propriedade esta utilizada em disciplinas como DSF.
As unidades de Momento de Inércia possuem a forma 𝐿4 , como por exemplo, 𝑚 4, 𝑘𝑚 4 , 𝑚𝑚 4 e
𝑝𝑜𝑙4 ;
São sempre positivos;
São aditivos, podem-se somar momentos de inércia diferentes desde que possuam o mesmo eixo
de referência, como se pode observar na figura a seguir:
𝐼𝑥 = 𝐼𝑥 1 + 𝐼𝑥 2 + 𝐼𝑥 3
1
Aula 02 – Figuras Planas II
Exemplo Resolvido 1: Cálculo do momento de inércia com relação ao eixo 𝑥̅ de um retângulo com sistema
de eixos localizados no centróide:
y
ℎ
ℎ
2
h
dy
x
𝑏𝑦 3 2
𝑏ℎ 3
� =
𝐼𝑥̅ = � 𝑦 2 𝑑𝐴 = � ℎ 𝑦 2 𝑏𝑑𝑦 =
3 −ℎ
12
𝐴
−
2
2
b
Exemplo Resolvido 2: Cálculo do momento de inércia com relação ao eixo 𝑥 de um retângulo com sistema
de eixos localizados na base:
y
h
ℎ
ℎ
𝑏𝑦 3
𝑏ℎ 3
� =
𝐼𝑥 = � 𝑦 𝑑𝐴 = � 𝑦 𝑏𝑑𝑦 =
3 0
3
𝐴
0
2
dy
2
x
b
Obs.: O momento de inércia com relação ao eixo 𝑦
� ou 𝑦, possui cálculo semelhante ao apresentado acima,
portanto, não será demonstrado.
1.2 – Translação de eixos: Teorema de Steiner ou dos Eixos Paralelos para o Momento de Inércia
Em muitas situações possuímos os momentos de inércia 𝐼𝑥̅ e 𝐼𝑦� fornecido com relação aos eixos 𝑥̅ e 𝑦� que
passam pelo centróide, porém, necessitamos do momento de inércia com relação a outros eixos quaisquer
𝑥 e 𝑦 paralelos a 𝑥̅ e 𝑦�, para tal faz-se necessário reescrever as coordenadas fornecidas no sistema
referencial 𝑥̅ 𝑦� no referencial 𝑥𝑦, como pode ser observado a seguir:
𝑥 = 𝑥̅ + 𝑏
𝑦 = 𝑦� + 𝑎
2
Aula 02 – Figuras Planas II
Recalculando o momento de inércia com relação ao eixo 𝑥, temos:
𝐼𝑥 = � 𝑦 2 𝑑𝐴 = � (𝑦� + 𝑎)2 𝑑𝐴 = � (𝑦� 2 + 2𝑎𝑦� + 𝑎2 )𝑑𝐴 = � 𝑦� 2 𝑑𝐴 + 2𝑎 � 𝑦�𝑑𝐴 + 𝑎2 � 𝑑𝐴
𝐴
𝐴
Sabe-se que:
𝐴
𝐴
𝐴
𝐴
𝐼𝑥̅ = � 𝑦� 2 𝑑𝐴
𝐴
𝑀𝑆𝑥̅ = � 𝑦�𝑑𝐴
𝐴
𝐴 = � 𝑑𝐴
𝐴
Na aula anterior, quando estudamos as propriedades do momento estático verificamos que quando o eixo
de referência passa pelo centróide, o momento estático é nulo, portanto podemos reescrever o momento
de inércia sob a seguinte forma:
𝐼𝑥 = 𝐼𝑥̅ + 𝑎 2 𝐴
De forma similar para o momento de inércia com relação ao eixo 𝑦, é dado por:
𝐼𝑦 = 𝐼𝑦� + 𝑏2 𝐴
Exemplo Resolvido 3: Cálculo do momento de inércia com relação ao eixo 𝑥 de um retângulo com sistema
de eixos localizados na base, calculado utilizando o Teorema de Steiner:
𝑏ℎ 3
ℎ 2
𝑏ℎ 3 𝑏ℎ 3 𝑏ℎ 3 + 3𝑏ℎ 3
𝑏ℎ 3
𝐼𝑥 = 𝐼𝑥̅ + 𝑎 𝐴 =
+ � � 𝑏ℎ =
+
=
=
12
12
4
12
3
2
2
1.3 – Raio de Giração com relação a um eixo
O raio de giração refere-se sempre a um eixo. Por definição o raio de giração com relação a este eixo é raiz
quadrada do momento de inércia dividido pela área.
Se fosse possível concentrar toda a área da figura plana em um ponto cuja distância ao centro de gravidade
seja o raio de giração, o momento de inércia com relação a um eixo que passe pelo CG seria a área
multiplicada pelo quadrado do raio de giração correspondente.
Raio de giração com relação ao eixo 𝑥:
𝐼𝑥
𝑖𝑥 = �
𝐴
Raio de giração com relação ao eixo 𝑦:
𝐼𝑦
𝑖𝑦 = �
𝐴
𝐼𝑥 = 𝑖𝑥 2 𝐴
3
𝐼𝑦 = 𝑖𝑦 2 𝐴
Aula 02 – Figuras Planas II
1.3.1 – Propriedades do Raio de Giração
•
•
Normalmente a notação utilizada para representar o momento de inércia é a letra 𝑖, porém, em
algumas bibliografias a letra 𝑟 também é utilizada.
As unidades do raio de giração possuem a forma 𝐿, como por exemplo, 𝑚, 𝑘𝑚, 𝑚𝑚 e 𝑝𝑜𝑙;
1.4 – Módulo de resistência com relação a um eixo central
O módulo de resistência é uma característica geométrica da seção que será utilizada no estudo da flexão.
Apesar de podermos definir o módulo de resistência com relação a qualquer eixo que passe pelo centro de
gravidade da figura plana, neste tópico o módulo de resistência será definido sempre com relação a um dos
eixos centrais da figura. Os módulos de resistência com relação ao eixo central 𝑢 são dados pelas
expressões:
𝑊𝑥𝑠 =
𝑊𝑥𝑖 =
𝐼𝑢
𝑐𝑠
𝐼𝑢
𝑐𝑖
onde:
𝐼𝑢 é o momento de inércia com relação ao eixo 𝑢;
𝑐𝑠 é a distância entre o eixo 𝑢 e o eixo paralelo a ele que tangencia a figura plana no lado superior (caso
haja mais de uma tangente, adota-se a que dá a maior distância);
𝑐𝑖 é a distância entre o eixo u e o eixo paralelo a ele que tangencia a figura plana no lado inferior (caso haja
mais de uma tangente, adota-se a que dá a maior distância).
1.4.1 – Propriedades do Módulo de Resistência
•
•
As unidades do módulo de resistência possuem a forma 𝐿3 , como por exemplo, 𝑚 3, 𝑘𝑚 3 , 𝑚𝑚3 e
𝑝𝑜𝑙3 ;
Os módulos de resistência não são aditivos, isto é, ao contrário do cálculo feito para o momento de
inércia, o módulo de resistência de uma seção tubular não é o módulo da parte de fora menos o
módulo da parte de dentro.
4
Aula 02 – Figuras Planas II
1.5 – Momento polar de inércia com relação a um ponto
O momento polar de inércia é sempre definido com relação a um ponto ou pólo. Tomamos o elemento de
área infinitesimal 𝑑𝐴 e multiplicamos pelo quadrado da distância ao polo e fazemos a integral em todo
domínio 𝐴.
Momento polar de inércia com relação ao pólo 𝑂:
𝐼𝑝 = � 𝑟 2 𝑑𝐴
𝐴
mas:
𝑟 2 = 𝑥2 + 𝑦 2
então:
𝐼𝑝 = � (𝑥 2 + 𝑦 2 )𝑑𝐴 = � 𝑥 2 𝑑𝐴 + � 𝑦 2 𝑑𝐴
𝐴
𝑂
𝐴
𝐼𝑝 = 𝐼𝑥 + 𝐼𝑦
𝐴
1.5.1 – Propriedades do Momento Polar de Inércia
•
O momento polar de inércia é sempre constante quando referenciado a um mesmo ponto, isto
ocorre devido ao fato da soma dos momentos de inércia com relação a eixos ortogonais entre si
que passam pelo mesmo ponto ser constante, como pode ser demonstrado na seqüência:
Definindo novamente 𝑟 2 , temos:
portanto:
𝑟 2 = 𝑥 2 + 𝑦 2 = 𝑢2 + 𝑣 2
𝐼𝑝 = 𝐼𝑥 + 𝐼𝑦 = 𝐼𝑢 + 𝐼𝑣
1.6 – Produto de Inércia com relação a um par de eixos
O produto de inércia é sempre calculado com relação a um par de eixos ortogonais entre si. Neste caso o
elemento de área 𝑑𝐴 é multiplicado pelas distâncias a cada um dos eixos e integrado em toda área 𝐴.
Geralmente o produto de inércia é calculado com
relação aos dois eixos de coordenadas, assim o
produto de inércia com relação aos eixos 𝑥 e 𝑦 é
definido pela integral:
𝐼𝑥𝑦 = � 𝑥𝑦𝑑𝐴
𝐴
5
Aula 02 – Figuras Planas II
1.6.1 – Propriedades do Produto de Inércia
•
•
•
Normalmente a notação utilizada para representar o produto de inércia é a letra 𝐼, porém, em
algumas bibliografias a letra 𝐽 também é utilizada, mas esta última normalmente refere-se ao
momento de inércia de massa, propriedade esta utilizada em disciplinas como DSF. Em alguns livros
o produto de inércia é chamado de momento centrífugo de inércia;
As unidades de Produto de Inércia possuem a forma 𝐿4 , como por exemplo, 𝑚 4, 𝑘𝑚 4 , 𝑚𝑚 4 e 𝑝𝑜𝑙4 ;
O Produto de Inércia pode ser positivo, negativo ou nulo como pode ser observado nas figuras a
seguir:
Para uma figura contida inteiramente no Para uma figura contida inteiramente nos
primeiro ou terceiro quadrantes o produto de segundo e quarto quadrante o produto de
inércia é positivo, pois todos os produtos 𝑥𝑦 inércia é negativo, pois todos os produtos 𝑥𝑦
serão positivos.
serão negativos.
𝐼𝑥𝑦 > 0
•
𝐼𝑥𝑦 < 0
Os produtos de inércia são aditivos, podem-se somar produtos de inércia diferentes desde que
possuam os mesmos eixos de referências, como se pode observar na figura a seguir:
𝑦
𝐼𝑥𝑦 = 𝐼𝑥𝑦 1 + 𝐼𝑥𝑦 2 + 𝐼𝑥𝑦 3
𝑥
1.7 – Translação de eixos: Teorema de Steiner ou dos Eixos Paralelos para o Produto de Inércia
De forma similar ao demonstrado para o momento de inércia podemos definir o produto de inércia com
relação a um par de eixos qualquer com base no produto de inércia com relação ao par de eixos que passa
pelo centróide, como pode ser observado a seguir:
𝐼𝑥𝑦 = 𝐼𝑥𝑦
���� + 𝑎𝑏𝐴
6
Aula 03 – Figuras Planas III
1- FIGURAS PLANAS
Nesta aula iremos estudar eixos e momentos principais de inércia e assim finalizar o estudo de figuras
planas.
1.1 – Eixos e momentos principais de inércia
Existem diversos eixos que passam pelo CG de uma figura plana, porém, existe um par de eixos que
possuem uma maior importância, são os eixos chamados de eixos principais. Esses eixos são importantes,
pois, fornecem o maior e o menor momento de inércia de uma figura plana.
Para se determinar esses eixos faz-se necessário conhecer os momentos e produtos de inércia com relação
a um par de eixos ortogonais qualquer que passa pelo CG de uma figura plana, a determinação da posição
desses eixos, bem como o valor dos momentos de inércia podem ser determinados pelas expressões a
seguir:
Assim como o momento estático já estudado na aula anterior, o momento de inércia também é sempre
relacionado a um eixo de referência. Tomamos o elemento de área infinitesimal 𝑑𝐴 e multiplicamos pelo
quadrado da distância a este eixo e fazemos a integral em todo domínio 𝐴.
Para os eixos cartesianos, os momentos de inércia podem ser definidos pelas seguintes integrais:
𝑢 = 𝑥 𝑐𝑜𝑠(𝛼 ) + 𝑦 𝑠𝑒𝑛(𝛼 )
𝑣 = 𝑦 𝑐𝑜𝑠(𝛼 ) − 𝑥 𝑠𝑒𝑛(𝛼 )
y
v
𝐼1 = 𝐼𝑚𝑎𝑥
dA
v
y
u
𝐼2 = 𝐼𝑚𝑖𝑛
u
α
x
x
1
𝐼𝑥 + 𝐼𝑦
𝐼𝑥 − 𝐼𝑦 2
�
=
+ �
� + 𝐼𝑥𝑦 2
2
2
𝐼𝑥 + 𝐼𝑦
𝐼𝑥 − 𝐼𝑦 2
�
=
− �
� + 𝐼𝑥𝑦 2
2
2
𝑡𝑎𝑛(𝛼1 ) =
𝐼𝑥 − 𝐼1
𝐼𝑥𝑦
𝛼2 = 𝛼1 + 90° = 𝛼1 +
𝜋
2
Aula 03 – Figuras Planas III
1.2 – Exercícios Figuras Planas
Para as figuras a seguir determine todas as propriedades das figuras planas (Área, 𝑀𝑆𝑥 , 𝑀𝑆𝑦 , 𝑋𝐺 , 𝑌𝐺 , 𝐼𝑥 , 𝐼𝑦 ,
𝐼𝑥𝑦 , 𝐼1 , 𝐼2 , 𝛼1 e 𝛼2 ).
𝑖)
y
1
7
1
4
x
2
Aula 03 – Figuras Planas III
3