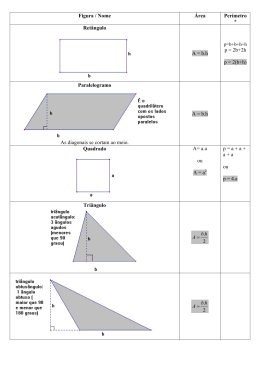
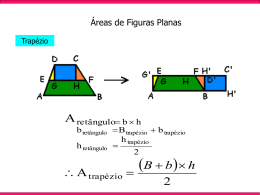
AUTOAVALIAÇÃO
01. Dadas as afirmações:
I. Quaisquer dois ângulos opostos de um quadrilátero são suplementares.
II. Quaisquer dois ângulos consecutivos de um paralelogramo são suplementares.
III. Se as diagonais de um paralelogramo são perpendiculares entre si e se cruzam em seu ponto médio, então este
paralelogramo é um losango.
Podemos garantir que:
a) Todas são verdadeiras.
b) Apenas I e II são verdadeiras.
c) Apenas II e III são verdadeiras
d) Apenas II é verdadeira.
e) Apenas III é verdadeira.
02. Sejam:
P: o conjunto dos retângulos
Q: o conjunto dos quadrados
L: o conjunto dos losangos
A figura que melhor representa as relações existentes entre eles é:
a)
b)
c)
d)
e)
03. Assinale a afirmação falsa:
a) se um losango tiver diagonais congruentes será quadrado.
b) se um retângulo tiver diagonais bissetrizes será losango.
c) em todo trapézio isósceles os ângulos adjacentes a uma mesma base são congruentes.
d) existe paralelogramo cujas diagonais são congruentes e não é eqüiângulo.
e) se um paralelogramo tiver as diagonais perpendiculares é eqüilátero.
04. Assinale a alternativa falsa:
a) em todo trapézio isósceles os ângulos opostos são suplementares.
b) todo trapézio retângulo é trapézio escaleno.
c) em todo losango as diagonais são perpendiculares.
d) as diagonais do retângulo são perpendiculares e congruentes.
e) se um losango tiver diagonais congruentes será um quadrado.
05. Verifique as proposições abaixo quando verdadeiras marque coluna I e quando falsas marque coluna II.
0
1
2
3
4
0
1
2
3
4
Todo trapézio retângulo é trapézio e é retângulo.
Todo losango é paralelogramo e todo quadrado é retângulo.
Se um losango for eqüiângulo obrigatoriamente será quadrado.
Se um retângulo for eqüilátero pode não ser quadrado.
Todo trapézio escaleno é trapézio retângulo.
06. Verifique a veracidade das afirmativas.
0
1
2
3
0
1
2
3
Se em um retângulo as diagonais forem bissetrizes o mesmo será um polígono regular.
Se em um losango as diagonais forem congruentes o mesmo será obrigatoriamente quadrado.
Se em um retângulo as diagonais forem perpendiculares o mesmo será quadrado.
Se em um paralelogramo as diagonais forem congruentes e não-perpendiculares o mesmo será um retângulo, mas
não será quadrado.
07. Julgue as proposições abaixo.
0
1
2
3
4
0
1
2
3
4
Todo quadrilátero inscritível é convexo.
Todo quadrilátero circunscritível é convexo.
Todo quadrado é losango e é retângulo.
Existe paralelogramo que não é trapézio.
Se um retângulo não for losango, é paralelogramo mas não é quadrado.
08. Analise as afirmações abaixo e marque na primeira coluna se for verdadeira e na segunda coluna se for falsa.
0
1
2
3
4
0
1
2
3
4
Se
Se
Se
Se
Se
em
em
em
um
um
um quadrilátero as diagonais forem perpendiculares o mesmo será losango.
um quadrilátero as diagonais forem congruentes o mesmo será retângulo.
um quadrilátero as diagonais forem congruentes e perpendiculares o mesmo será quadrado.
quadrilátero for eqüiângulo será retângulo.
quadrilátero for eqüilátero será losango.
09. Analise as afirmações abaixo e marque coluna I quando verdadeiras e coluna II quando falsas:
0
1
2
3
4
0
1
2
3
4
Todo quadrilátero é inscritível.
Todo quadrilátero é circunscritível.
Todo triângulo é inscritível e circunscritível.
Se um quadrilátero for circunscritível seus ângulos opostos são suplementares.
Se um quadrilátero for inscritível as somas das medidas de seus lados opostos são iguais.
10. Verifique a veracidade das afirmativas:
0
1
2
3
4
0
1
2
3
4
Todo trapézio isósceles é inscritível.
Todo losango é circunscritível.
Todo trapézio isósceles cuja base média tem medida igual a um dos lados não paralelos é circunscritível.
Dado um retângulo qualquer é sempre possível inscrevê-lo em uma circunferência.
Se um retângulo for circunscritível obrigatoriamente será quadrado.
11. Julgue os itens abaixo e marque coluna I quando verdadeiro e coluna II quando falso.
0
1
2
3
4
0
1
2
3
4
Quando uma circunferência circunscreve um losango o mesmo é retângulo.
Um trapézio retângulo jamais ficará inscrito em uma circunferência.
Existe paralelogramo não-inscritível e não-circunscritível.
Todo quadrado é inscritível e circunscritível.
Se um quadrilátero estiver inscrito em uma circunferência seus ângulos opostos são suplementares.
12. Analise as afirmações.
0
1
2
3
4
0
1
2
3
4
Em uma circunferência todo diâmetro é uma corda.
Se uma corda de circunferência for diâmetro as flechas correspondentes serão raios.
Toda semi-circunferência é um arco.
O centro da circunferência sempre pertence à circunferência.
Toda reta normal à circunferência obrigatoriamente passa pelo centro da circunferência.
13. Verifique a veracidade das afirmativas.
0
1
2
3
0
1
2
3
4
4
Toda reta tangente à circunferência é sempre perpendicular ao raio cuja extremidade é o ponto de tangência.
Toda reta secante à circunferência é uma reta normal à circunferência.
Toda reta normal à circunferência é uma reta secante à circunferência.
Se uma reta é tal que a distância do centro da circunferência a esta reta é maior que a medida do raio, a reta é
exterior à circunferência.
Se por um ponto externo a uma circunferência conduzirmos duas tangentes distintas à circunferência, este ponto é
eqüidistante dos pontos de tangência.
14. ABCD é um trapézio. AB = 23cm e CD = 37cm. Sendo M e N médios de AD e de BC, respectivamente, calcule MN e PQ.
15. Analise as afirmações:
0
0
1
1
2
3
4
2
3
4
Se duas circunferências são secantes entre si, a distância entre seus centros é sempre menor que a soma das
medidas dos raios e maior que a diferença absoluta.
Em todo triângulo retângulo circunscritível o raio da circunferência inscrita tem medida igual à semi-diferença entre
a soma das medidas dos catetos e a medida da hipotenusa.
Em todo quadrilátero inscritível os ângulos opostos são suplementares.
Em todo quadrilátero circunscritível a soma das medidas dos pares de lados opostos são iguais.
Se duas circunferências são concêntricas não existe distância entre seus centros.
16. As afirmações abaixo são relativas à quadriláteros:
0
1
2
3
4
0
1
2
3
4
Em todo trapézio a soma da base média com a mediana de Euller é sempre igual à base maior.
Se um losango tiver diagonais congruentes será um quadrado.
Todo trapézio retângulo é trapézio escaleno e possui os ângulos não congruentes suplementares.
Se um losango for quadrado terá obrigatoriamente diagonais congruentes.
Se um quadrilátero tiver diagonais congruentes e perpendiculares pode não ser quadrado.
17. Dentre as afirmações abaixo, feitas sobre quadriláteros, marque coluna I para as verdadeiras e coluna II para as falsas.
0
0
1
2
3
4
1
2
3
4
Se em um quadrilátero as diagonais forem perpendiculares, congruentes e cortarem-se ao meio, o mesmo é
necessariamente quadrado.
Todo trapézio escaleno é trapézio retângulo, mas nem todo trapézio retângulo é escaleno.
Se um losango tiver diagonais congruentes será um quadrado.
Todo quadrado é losango e também é retângulo.
Em todo trapézio isósceles os ângulos adjacentes a uma mesma base são congruentes.
18. Nesta figura, os ângulos â, b̂, ĉ e d̂ medem respectivamente
x
3x
, 2x,
e x. O ângulo ê é reto. Qual a medida do ângulo f̂ ?
2
2
a) 16º
b) 18º
c) 20º
d) 22º
e) 24º
19. Na figura, tem-se m(BÂD) = 108º e m(A D̂ C) = 112º. A medida de E B̂ C é:
a) 68º
b) 72º
c) 108º
d) 112º
e) n.d.a.
20. Seja ABCD um trapézio retângulo. O ângulo formado pelas bissetrizes do seu ângulo reto e do ângulo agudo adjacentes à
base maior mede 92º. Os ângulos agudo e obtuso deste trapézio medem respectivamente:
a) 88º, 92º
b) 86º, 94º
c) 84º, 96º
d) 82º, 98º
e) 79º, 101º
21. As bases de um trapézio isósceles circunscrito a uma circunferência medem 9 m e 6 m. Cada um dos outros dois lados do
trapézio mede:
a) 4,5 m
b) 6 m
c) 7,5 m
d) 8 m
e) n.d.a.
22. Num quadrilátero ABCD, o ângulo Ĉ é igual a 1/3 do ângulo B̂ , o ângulo  mede o quíntuplo do ângulo Cˆ e o ângulo D̂ vale
45º. Pode-se dizer que  - B̂ vale:
a) 50º
b) 60º
c) 70º
d) 80º
e) 90º
E
23. Na figura ABCD é um quadrado, ADE e ABF são triângulos eqüiláteros. Se os pontos C, A e M
M
são colineares, então o ângulo FÂM mede:
A
D
a) 75º
b) 80º
c) 82º 30’
d) 85º
e) 87º30’
F
C
B
B
24. Na figura ao lado o complemento do ângulo x é:
a) 45º
b) 55º
c) 65º
d) 15º
e) 85º
3x
x
C
A
2x
D
2x - 20°
25. Na figura AP , BP , CQ e DQ têm como suporte as bissetrizes dos ângulos internos do
quadrilátero ABCD, logo, o valor de x + y é:
a) 162°
b) 180°
c) 135°
d) 189°
e) 126°
26. O triângulo APB é isósceles de base AB , então podemos afirmar que o suplemento de x é:
a) 90º
b) 100º
c) 110º
d) 145º
e) 130º
27. ABCD é um trapézio retângulo circunscrito a uma circunferência de raio r. Calcule r, sabendo
que AB = 20, CD = 30 e AD = 26.
28. ABCD, na figura, está circunscrito à circunferência de centro Q. Sabendo que AB = 3x, BC = 4x + 1, CD = 5x e DA = 2x + 3,
calcule o perímetro desse quadrilátero.
29. Duas tangentes são traçadas a um círculo de um ponto exterior A e tocam o círculo
nos pontos B e C, respectivamente. Uma terceira tangente intercepta o segmento
AB em P e AC em R e toca o círculo em Q. Se AB = 20 cm, então o perímetro do
triângulo APR, em cm, é igual a:
a) 39,5
b) 40
c) 40,5
d) 41
e) 41,5
30. Na figura, AB é diâmetro da circunferência. O menor dos arcos (AC) mede:
a) 100º
b) 120º
c) 140º
d) 150º
e) 160º
31. As semi-retas PM e PN são tangentes ao círculo da figura e a medida do arco MGN é 4 vezes
a do arco MFN. O ângulo
MP̂N
a) 76º
c) 90º
b) 80º
vale:
a) 108º
e) 120º
32. O pentágono ABCDE ao lado está inscrito em um círculo de centro O. O ângulo central CÔD mede 60º. Então x + y é igual a:
a) 180º
x
b) 185º
c) 190º
d) 210º
e) 250º
y
A
33. Na figura abaixo, o triângulo ABC é isósceles e BD é a bissetriz do ângulo de vértice
θ
35°
B. A medida θ, do ângulo assinalado, é:
a) 55º
b) 50º
D
c) 45º
d) 40º
e) 35º
B
C
34. Se, na figura, AB = 20º, BC = 124º, CD = 36º e DE = 90º, então o ângulo x mede:
a) 34º
b)35º30’
c)37º
d)38º30’
e)40º
x
35. Em um dado triângulo retângulo inscrevemos uma circunferência de diâmetro d e circunscrevemos outra de diâmetro D.
O perímetro do triângulo vale:
a) d + D
b) 2d + D
c) d + 2D
d) 3/2(d + D)
e) 2(d + D)
36. Os pontos A, B e C pertencem a uma circunferência de centro O. Sabe-se que OA é perpendicular a OB e forma com BC um
ângulo de 70º. Então, a tangente à circunferência no ponto C forma com a reta OA um ângulo de:
a) 10º
b) 20º
37. Na figura abaixo o ângulo x mede:
a) 135°
b) 130° 30’
c) 75º
d) 145º
e) 3π rad
4
c) 30º
d) 40º
e) 50º
P
38. Na figura,
α
AB é um diâmetro, a corda AM é o lado do triângulo eqüilátero
N
inscrito e BN , o lado do quadrado inscrito. Calcule o ângulo α, formado pelas
tangentes PM e PN . (Em graus)
A
B
O
M
39. Na figura abaixo o arco AB mede: (Em graus)
→
→
40. As circunferências são tangentes externamente em Q e PA e PB são tangentes às circunferências.
Determine a medida do ângulo AQ̂B onde t é tangente comum e AP̂B = 80º.
a) 100º
b) 110º
c) 120º
d) 140º
e) 150º
GABARITO
01 – C
02 – C
03 – D
04 – D
05 – FVVFF
16 – VVVVV
21 – C
06 – VVVV
07 – VVVFV
14 – MN = 30cm
15 – VVVVF
PQ = 7cm
22 – C
23 – A
09 – FFVFF
10 – VVVVV
11 – VVVVV
12 – VVVFV
13 – VFVVV
17 – VFVVV
18 – B
19 – D
20 – B
08 – FFFVV
24 – B
25 – B
26 – D
27 – 12
28 – 32
29 – B
30 – A
31 – D
32 – D
33 – D
34 – C
35 – C
36 – D
37 – D
38 – 30
39 – 80
40 – D