A ESTRUTURA DO ÁTOMO.
tópico I
1.1 Átomos com apenas um elétron.
As autofunções para sistemas atômicos monoeletrônicos são funções do tipo

( r )  R n , (r)Y,m ()
(1.1.1)
onde as funções R n , (parte radial) são produtos de exponenciais e polinômios de Laguerre, e as
funções Y ,m (parte angular) são os harmônicos esféricos (   (, ) ). As coordenadas
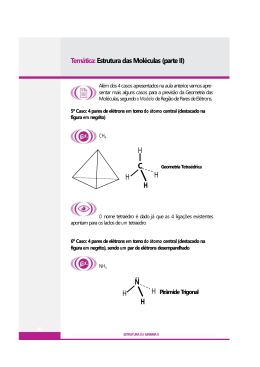
esféricas (r, , ) estão indicadas na figura 1 abaixo
z

r
y

x
Figura 1. Coordenadas esféricas (r ,  , ) com relação às coordenadas cartesianas (x , y , z). r é o módulo do vetor

posição r ,  é o ângulo que este forma com o eixo z e  é o ângulo que sua projeção no plano xy forma com o eixo
x.
Os números quânticos n, , m satisfazem as condições
n  1,2,3, ( número quântico principal)
  0,1,2,, n  1 ( número quântico orbital )
m  ,  1,,0,,   1,  ( número quântico magnético )

As funções de onda ( r ) na expressão (1.1.1) são soluções da equação de Schrödinger
H  E
(1.1.2)
onde
H
2
Ze2
2 
2m e
r
(1.1.3)
é o hamiltoniano monoeletrônico e os autovalores E são dados por
E
1 Z2mee4
2 2n 2
(1.1.4)
Essas funções de onda devem também satisfazer o requisito da normalização
    dV  1
(1.1.5)
ou seja
d


R
r
dr
Y
Y
sen

d
 d  1
, m



2 
2
2
n ,
0

, m
0 0
1.2.Átomos com mais de um elétron.
(1.1.6)
De acordo com o princípio aufbau, em sistemas atômicos multieletrônicos os orbitais
atômicos são preenchidos em ordem crescente de energia e respeitando-se o princípio de Pauli.
Neste procedimento o spin do elétron é fundamental. Cada elétron passa a ocupar um spinorbital que é especificado pela quadra (n, , m, ms ), onde ms =  ½. Dessa forma constroem-se
as configurações eletrônicas: 1s1, para o hidrogênio; 1s2, para o hélio; 1s22s1, para o lítio, e assim
por diante. O conceito de configuração eletrônica, embora seja muito interessante e útil, deve ser
entendido com certo cuidado. Na descrição quântica usual da estrutura de átomos com mais de
um elétron as funções de onda são consideradas como combinações lineares das funções
correspondentes às diversas configurações eletrônicas. Voltaremos a esse ponto mais adiante.
De um ponto de vista mais formal, as funções de onda de sistemas atômicos com mais de um
elétron são autofunções do hamiltoniano não relativístico
2
H
2m e
N
N
  
2
i
i
i
Ze2 1 N e 2
 
ri
2 i  j rij
(1.2.1)
onde N é o número de elétrons, ri é a distância entre o elétron i e o núcleo e ri j a distância entre
os elétrons i e j. O termo de repulsão coulombiana entre os elétrons, e2/ri j , faz com que cada
elétron não mais se encontre em um potencial esferossimétrico. Se esse termo não existisse, a
equação de Schrödinger para um sistema atômico multieletrônico teria uma solução exata.. As
autofunções seriam produtos de funções hidrogenóides do tipo mostrado na expressão (1.1.1), e
os autovalores seriam somas de energias dadas pela equação (1.1.2). Nesse caso o princípio
aufbau teria uma forma interessante: a configuração fundamental do lítio, por exemplo, tanto
poderia ser 1s22s1 como 1s22p1, pois não haveria diferença de energia entre subcamadas com o
mesmo n.
A repulsão coulombiana, que não pode ser negligenciada, torna a resolução da equação
de Schrödinger num problema muito complexo. Porém, são conhecidos hoje em dia métodos que
permitem resolvê-la de modo aproximado, tais como o método de Hartree-Fock e tratamentos
perturbativos. Em geral, nesses métodos parte-se de um conjunto de funções de base que são os
spin-orbitais. Assume-se que uma solução inicial aproximada da equação de Schrödinger é dada
por uma combinação linear apropriada de produtos desses spin-orbitais. Essa combinação linear,
 

( r1 , r2 ,, rN ) , quando normalizada, fornece uma energia que é dada pela equação
E     H dV
(1.2.2)
onde dV é o elemento de volume em 3N dimensões. A equação acima é a chamada forma
integral da equação de Schrödinger. A função de onda  deve expressar o fato de que os elétrons
são partículas indistinguíveis fermiônicas (spin semi-inteiro), e que, portanto, seguem o princípio
de Pauli. Em outras palavras,  deve ser uma função anti-simétrica com relação a troca (
permutação) de elétrons e deve se anular sempre que a dois elétrons quaisquer corresponda o
mesmo spin-orbital.
Uma função de onda desse tipo, segundo a proposta de Slater, pode ser dada na forma de
um determinante, o assim chamado determinante de Slater. Seja n1, 1, m1, ms1, n2, 2, m2,
ms2, , nN, N, mN, msN um conjunto de N spin-orbitais (lembrando que msi =  ½ para
qualquer i ). Vamos usar, para efeito de simplificação, a notação ni, i, mi, msi = i. Vamos,
em seguida, ocupar esses N spin-orbitais com N elétrons. A notação ij indica que o elétron j
está ocupando o spin-orbital i. É importante lembrar que os elétrons são partículas indistinguíveis
e, portanto, o elétron j pode ser qualquer um dos N elétrons. O determinante de Slater é, nesse
caso, dado por
 1
 
 N! 
1/ 2
11 12
21 22


N1 N2

1N
2N




(1.2.3)
NN
O fator (1/N!)1/2 é o fator de normalização. Vejamos um exemplo. Consideremos o átomo de
hélio e sua configuração eletrônica fundamental 1s2. Os spin-orbitais são: 1,0,0,+1/2 e 1,0,0,1/2, ou simplesmente +1/2 e -1/2. Teremos então
1 {1 / 2}1 {1 / 2}2
1
(1,2) 

{1 / 2}1{1 / 2}2  {1 / 2}2 {1 / 2}1
1
2
2 {1 / 2} {1 / 2}
2


(1.2.4)
Podemos aproveitar esse exemplo para o seguinte. No caso da configuração 1s2 temos
apenas dois spin-orbitais, os quais estão ocupados pelos dois elétrons do átomo de hélio. A essa
configuração eletrônica corresponde um, e só um, determinante de Slater, dado pela expressão
logo acima. Suponha que ao invés da configuração fundamental 1s2 tivéssemos considerado a
configuração excitada 1s12p1. Nesse caso teríamos oito spin-orbitais (dois da subcamada 1s e seis
da subcamada 2p). Como temos dois elétrons, poderíamos construir doze determinantes de
Slater, dois  dois, para essa configuração. Na construção desses determinantes obviamente um
dos spin-orbitais deve pertencer à subcamada 1s e o outro à subcamada 2p. Cada um desses
determinantes corresponde a um microestado.
Voltemos agora a alguns parágrafos atrás onde comentamos que a função de onda de um
dado estado multieletrônico é dada por uma mistura de configurações eletrônicas. Em termos de
microestados isto corresponde a dizer que tal função é dada por
   ci  i
(1.2.5)
i
onde as funções  i são determinantes de Slater. A combinação linear acima inclui os
microestados de todas as possíveis configurações eletrônicas. Na prática alguns coeficientes c
são identicamente nulos e outros são muito pequenos. Em geral faz-se um corte (chama-se
também “truncagem”) na soma na equação (1.2.5), tendo-se em mente que quanto mais
microestados   puderem ser incluídos mais precisa será a função  . Existem métodos bem
conhecidos na literatura que permitem construir de modo adequado os spin-orbitais {i}, e
consequentemente os determinantes   , assim como permitem calcular os coeficientes c para
sistemas atômicos multieletrônicos [ ].
1.1. Momento angular


O momento angular  de um objeto com vetor posição r e quantidade de movimento

p é definido por
  
 rp
(1.3.1)
Essa quantidade aparece frequentemente nas equações de movimento de um sistema, clássico ou
quântico. Neste último caso o momento angular de uma dada partícula tem a forma
 

  r  (i )
(1.3.2)

onde  é o operador gradiente com relação a um dado sistema de coordenadas. Com relação a
um sistema de coordenadas esféricas, mostrado na figura 1, o hamiltoniano de um sistema
atômico hidrogenóide é dado por
H
2
2m e
 1   2   1 ˆ 2  Ze2
r
 2 2
 2
r
 r r  r  r  
(1.3.3)
onde o operador quadrado do momento angular é dado por
2 
ˆ 2   2  1   sen     1


  sen 2   2 
 sen   
(1.3.4)
ˆ 2 e ˆ (a
Pode-se mostrar que os harmônicos esféricos Y,m () são autofunções de 
z
componente z do operador momento angular), onde
ˆ  i  
z

(1.3.5)
As respectivas equações de autovalores são
ˆ 2 Y,m ()  (  1) 2 Y,m ()
e
(1.3.6)
ˆ Y ()  m Y ()
z ,m
,m
(1.3.7)
ˆ 2 e ˆ só atuam nas
onde os números quânticos  e m foram definidos na seção 1.1. Como 
z
coordenadas angulares ( e ), as funções R n , (r )Y,m () também são autofunções destes
operadores. Na mecânica quântica isso é equivalente a dizer que esses dois operadores comutam
ˆ ]  [H , ˆ z ]  0 .
com o hamiltoniano H, ou seja, [H , 
2
Para um sistema multieletrônico o momento angular orbital total é dado por


 
L   ri  p i    i
i
(1.3.8)
i
assim como o momento angular de spin total é dado por


S   si
(1.3.9)
i
Como já mencionado logo acima, é bem conhecido na mecânica quântica que se dois
operadores comutam então existe um conjunto completo de funções que são simultaneamente
autofunções desses dois operadores. Isto é de grande utilidade no sentido de que se queremos
encontrar as soluções da equação Â n  a n  n , que eventualmente é uma equação
complicada, podemos trabalhar com um operador B̂ , que comuta com  , tal que as soluções
de B̂ n  b n  n sejam encontradas de modo mais conveniente. Em nosso caso, que é o que se
ˆ 2 e ˆ .
faz na espectroscopia atômica, buscamos autofunções de H através de autofunções de 
z
1.4 Soma de momentos angulares. Os coeficientes de Clebsch – Gordan.
Em sistemas atômicos com simetria esférica (átomos ou íons livres) o operador
hamiltoniano comuta com o operador quadrado do momento angular e com o operador que
corresponde à sua projeção no eixo z. Portanto, as autofunções destes dois últimos operadores
são também autofunções do hamiltoniano do sistema atômico. Isto, na realidade, decorre das
propriedades de simetria de um sistema esférico.
De modo genérico, na mecânica quântica o operador momento angular, Ĵ , é tal que as
seguintes regras de comutação são satisfeitas:
[ Ĵ x , Ĵ y ]= i  Ĵ z
[ Ĵ y , Ĵ z ]= i  Ĵ x
(1.4.1)
[ Ĵ z , Ĵ x ]= i  Ĵ y
e
[ Ĵ z , Ĵ  ]=   Ĵ 
(1.4.2)
[ Ĵ +, Ĵ -]= 2  Ĵ z
onde
Ĵ   Ĵ x  i Ĵ y são os chamados operadores de levantamento (+) e abaixamento (-).
Além disso, temos as seguintes relações:
Ĵ 2 JM  J(J  1) 2 JM
(1.4.3)
Ĵ z JM  M  JM
e
Ĵ  JM   (J  M  1)(J  M) J M  1
Ĵ  JM   (J  M  1)(J  M) J M  1
(1.4.4)
Podemos dizer que as equações (1.4.1-4) acima constituem a definição de momento angular na
mecânica quântica. As funções
JM , que estão dadas na representação de momento
2
angular, são autofunções de Ĵ e Ĵ z , como mostram as equações (1.4.3). J e M são números
quânticos (inteiros ou semi-inteiros) que especificam o estado de momento angular, M
indicando a sua projeção no eixo z. Os possíveis valores de M são limitados pelo valor de J da
seguinte forma : M  J ,  J  1, , J  1, J . Se Ĵ corresponde ao momento angular de um
2
sistema atômico isolado então [ H, Ĵ ] = 0 e [ H, Ĵ z ] = 0 ; as autofunções de Ĵ
2
e Ĵ z são
tambem autofunções de H. Se diz, neste caso, que J é um bom número quântico (o significado
dessa expressão ficará claro mais adiante).
Vamos agora supor que temos um sistema constituído de duas partes (duas partículas, por


exemplo, ou o espaço orbital e o espaço de spin) com momentos angulares J 1 e J 2 . Há,



portanto, um momento angular resultante J  J1  J 2 . A questão que se coloca aqui é a
2
2
seguinte: conhecendo-se as autofunções de Ĵ 1 , Ĵ 1z , Ĵ 2 e Ĵ 2 z , como encontrar as autofunções
2
de Ĵ e Ĵ z  Este é um procedimento bem conhecido na mecânica quântica e chama-se adição
de momento angular. Neste procedimento procura-se combinações lineares, dos produtos
J 1 M1 J 2 M 2 , que sejam autofunções de Ĵ 2 e Ĵ z . Tais combinações têm a seguinte forma:
J1J 2 JM 
JMJ
1
1 2
M 2 J1J 2 JM J1M1 J 2 M 2
(1.4.5)
M1 , M 2
Os coeficientes J 1 M1 J 2 M 2 J 1 J 2 JM
são os chamados coeficientes de Clebsch-Gordan.
Eles constituem uma transformação unitária, entre a base { J 1 M1 J 2 M 2 } e a base
{ J 1 J 2 JM }, e têm algumas propriedades dentre as quais duas são mais importantes: quando as
condições
J1  J 2  J  J1  J 2
e
(1.4.6)
M  M1  M 2
(1.4.7)
não são satisfeitas estes coeficientes se anulam. A condição (1.4.6) também pode ser expressa
como
J  J1  J 2 , J1  J 2  1 ,, J1  J 2
(1.4.8)
ou seja, dados J 1 e J 2 , estes são os únicos valores que J pode assumir para que J 1 J 2 JM seja
2
autofunção de Ĵ e Ĵ z .
Uma imagem vetorial clássica desse procedimento seria a seguinte:
Figura 2. Representação clássica da soma de dois momentos angulares.
 

Devemos notar que, pela quantização do momento angular, os vetores J , J 1 e J 2 não podem
estar na direção z pois os valores máximos permitido a M, M 1 e M 2 são, respectivamente,
J, J 1
e
J2
enquanto
que
os
respectivos
módulos
destes
vetores
são
 J(J  1) ,  J 1 (J 1  1)
 J 2 (J 2  1) . Pela figura acima pode-se ver que
 
cos   M / J(J  1) . Com a adição J1  J 2 , estes dois vetores passam a ter um movimento

de precessão em torno de J , e este, por sua vez, em torno de z. Isto pressupõe que há uma
e
interação que conecta as partes 1 e 2 do sistema. É importante salientar que esta imagem vetorial
clássica, embora útil, não deve ser considerada como a realidade do ponto de vista quântico. Em
termos quânticos dizemos que M 1 e M 2 não são mais bons números quânticos ; os estados de
momento angular definidos por estes números se misturam (como expresso pela combinação
2
linear na equação (1.4.5)). Contudo, as autofunções J 1 J 2 JM são também autofunções de Ĵ 1 e
Ĵ 22 , mas não de Ĵ 1z e Ĵ 2 z . O hamiltoniano do sistema comuta com Ĵ 2 , Ĵ z , Ĵ 12 e Ĵ 22 .
O procedimento para soma de três ou mais momentos angulares será discutido mais
adiante na seção 1.7.
1.5 Termos espectroscópicos
A título de aplicação dos conceitos apresentados na seção precedente consideremos a
configuração eletrônica excitada 1s12p1 do átomo de hélio. Os dois momentos angulares orbitais
envolvidos são  1  0 (orbital s) e  2  1 (orbital p). Note que estamos usando a terminologia
em que o momento angular é denominado pelo número quântico que o define. Segundo a relação
(1.4.8) o momento angular resultante é tal que L só pode assumir o valor igual a 1. Na linguagem
da espectroscopia atômica se diz um estado P (para L=0 temos um estado S, para L=2 um estado
D e assim por diante, seguindo-se uma nomenclatura análoga àquela utilizada para o caso dos
orbitais hidrogenóides s, p, d, etc.). Os momentos angulares de spin são s1  s 2  1 / 2 e,
portanto, os possíveis valores de S (o momento angular de spin resultante) são S = 0 e 1. Temos
assim dois estados de spin para o mesmo estado de momento angular orbital resultante, ou dois
multipletos. Na linguagem da espectroscopia, os estados especificados pelos valores de S e L
chamam-se termos espectroscópicos. Estes são representados pela notação
2S+1
L , onde (2S+1)
é multiplicidade do termo, ou seja, o número de possíveis valores de MS para um dado S (pela
definição de momento angular M S  S ,S  1, , S  1, S ). A cada termo espectroscópico,
por sua vez, corresponde um número de estados dado por (2S+1)(2L+1), os quais são os estados
produtos SM S LM L ou, numa notação mais concisa, SM S LM L . Neste exemplo temos
então dois termos espectroscópicos: o 1P (S = 0, singleto P) e o 3P (S = 1, tripleto P).
O número total de estados, correspondendo aos termos espectroscópicos, é dado pela
soma abaixo,
Número total de estados =
 (2S  1)(2L  1)
(1.5.1)
termos
No caso do exemplo logo acima ele é 3 + 9 = 12, que é justamente o número de microestados da
configuração 1s12p1, como vimos antes.
A toda configuração eletrônica corresponde um certo número de termos espectroscópicos
e o número total de estados SM S LM L
deve ser igual ao número de microestados da
configuração. Isso está diretamente ligado com o princípio da exclusão de Pauli e significa que
nem sempre todos os estados obtidos a partir da soma de momentos angulares são aceitáveis,
pois alguns deles podem violar o princípio da exclusão. Consideremos, por exemplo, a
configuração 1s2 do He. Pela soma de momentos angulares teríamos dois termos: 1S e 3S.
Entretanto, o tripleto S (3S) viola o princípio da exclusão, pois ele pressupõe um microestado
com os dois spins emparelhados no mesmo orbital (1s), ou seja, para este microestado os dois
elétrons estariam ocupando o mesmo spin-orbital. Portanto, para esta configuração só o
singleto S (1S) é permitido. O número de microestados da configuração 1s2 é igual a 1, que é o
número de estados do termo permitido 1S. No caso da configuração 1s12p1 os dois termos 1P e 3P
são permitidos, pois como os elétrons ocupam spin-orbitais com n’s e  ’s diferentes não há
problema com relação a violação do princípio de Pauli.
Os estados SM S LM L , correspondentes aos termos espectroscópicos permitidos, são
combinações lineares de microestados (determinantes de Slater). Os coeficientes desta
combinação estão diretamente ligados aos coeficientes de Clebsch-Gordan. Vejamos um
exemplo disto. Seja uma configuração eletrônica do tipo n n   . Do ponto de vista de soma
1
de momentos angulares temos
1
LM L 
 m m LM
m , m
nm n  m
L
(1.5.2)
e
SM S 

ms , ms
1
2
ms
1
2
ms
1 1
2 2
SM S
1
ms
2
1
2
ms
(1.5.3)
o que leva à
SM SLM L 
 mm LM
m , m, m s , ms
1
2
L
ms
1
2
1
2
ms 1 2 ms
1 1
2 2
SM S nm nm 
ms
(1.5.4)
A combinação linear (1.5.4) acima não garante que os estados SM S LM L
satisfaçam o
princípio da exclusão e, portanto, estes podem corresponder a termos espectroscópicos não
permitidos. O procedimento correto consiste em considerar combinações lineares do tipo
SM S LM L
permitido
 mm LM

m , m, ms , ms
L
1
2
ms
1
2
ms
1 1
2 2
SM S 
(nm m s , n  mms )
onde  representa um determinante de Slater (um microestado) dado por

{nmm s }1
{nmm s }2
1
2
2 {n  m m s } {n  m m s }
1
no qual os spin-orbitais são
{nmm s }  nm
1
2
m s  nm 1 2 m s
e
{n mms }  n m
1
2
ms  n m 1 2 ms
(1.5.5)
Consideremos novamente o caso da configuração 1s12p1. O estado 0010 do singleto P, por
exemplo, tem S  0 , M S  0, L  1 e M L  0 . Em termos da expressão (1.5.5), tendo em
vista as condições (1.4.6) e (1.4.7) de não nulidade, os únicos coeficientes de Clebsch-Gordan
envolvidos são 0010 0110  1 e
1
2 ms
1
2 ( m s )
1 1 00
2 2
 (1)
1 m
s
2
1
2 . Portanto,
não é difícil verificar que
0010 
1
2
[(100 1 2 , 210( 1 2))  (100( 1 2) , 210 1 2)]
(1.5.6)
É importante perceber que embora as autofunções aqui descritas estejam especificadas somente
pelos números quânticos de momento angular, elas têm uma parte radial que normalmente é
especificada pelos números quânticos n e  . Além disso, como veremos mais adiante, nem
sempre uma autofunção é definida sem ambigüidade pelos números quânticos de momento
angular. Por isso é comum utilizarmos símbolos adicionais que representam outros números
quânticos necessários para especificar uma autofunção sem ambigüidade, como por exemplo:
SM S LM L
, onde  está representando tais números quânticos, inclusive os n’s e  ’s que
especificam a parte radial desta autofunção.
Encontrar os termos espectroscópicos permitidos de uma dada configuração eletrônica é,
em geral, uma tarefa trabalhosa quando se tem subcamadas com mais de um elétron. Dispomos,
hoje em dia, de tabelas que mostram os termos permitidos para praticamente todas as
configurações de interesse, além de programas computacionais simples que realizam essa tarefa
rapidamente. Estaremos particularmente interessados em configurações do tipo [ ]n f
N
, que são
as configurações dos íons terras raras (orbitais f ), onde [ ] representa camadas e sub-camadas
3
fechadas, ou o caroço de uma configuração; por exemplo [ Nd3+] = [ Xenônio]4 f . Os elétrons
da subcamada incompleta, ou de valência, são chamados de elétrons opticamente ativos.
De acordo com o princípio da exclusão de Pauli, podemos notar que o caroço não
contribui para os momentos angulares resultantes das configurações eletrônicas, visto que os
únicos valores possíveis de M S e M L são M S   m s  0 e M L   m   0 , e, portanto
S  0 e L  0 . Em outras palavras, se tivéssemos só o caroço o único termo permitido seria um
1
S . Assim, ao procurarmos os termos permitidos de uma configuração, basta nos preocuparmos
com as subcamadas incompletas. Porém, é preciso ter em mente que as possíveis energias
(autovalores) do sistema atômico dependem dos elétrons do caroço.
Vejamos, através de um exemplo simples, o procedimento usual para se encontrar os
termos permitidos de uma eletrônica. Consideremos uma configuração do tipo [caroço]np2, ou
por simplicidade de notação np2. Quando os elétrons em subcamadas incompletas têm o mesmo
n e mesmo  dizemos que são elétrons equivalentes. O procedimento consiste em montar um
quadro tendo os possíveis valores de M L e de MS como linhas e colunas. Cada par ( M L , MS )
especifica uma casa neste quadro. Em cada casa se colocam os microestados compatíveis com os
valores de M L e MS e com o princípio de Pauli. No caso da configuração np2, de acordo com a
relação (1.4.8), os possíveis valores de L e S são L = 2 , 1 , 0 ( D, P e S ) e S = 1 , 0 ( tripleto e
singleto ). Portanto, sem especificar os termos 2S+1L , ML  2 ,  1, 0 ,1, 2 e MS  1, 0 ,1 . Como
os elétrons são equivalentes podemos usar a notação ( m , m ) para indicar os microestados.
Assim, por exemplo, (1 , 0 ) indica um microestado formado pelos spin-orbitais {n , 1 , -1, ½} e {n , 1 , 0 , + ½}. Note que estamos aqui ignorando o caroço da configuração eletrônica,
pois só estamos interessados na obtenção de seus termos espectroscópicos.
O quadro abaixo ilustra o procedimento. Note que na casa correspondente a ML  2 e
MS  1 , por exemplo, não há microestados, caso contrário o princípio de Pauli seria violado.
Todos os possíveis microestados são mostrados. Para N elétrons equivalentes o número de
microestados é dado por
No de microestados (elétrons equivalentes) =
No caso em questão (np2) são 15.
(4  2)!
N!(4  2  N)!
(1.5.7)
ML
MS
1
0
+
2
-1
-
(1 , 1 )
1
D
(1+, 0+)
1
3
(1+, 0-)
1
P
D , 3P
(1+, -1+)
0
3
3
P
3
D , 3P, 1S
(-1+, 0+)
-1
(1-, 0-)
P
(1+, -1-) (1-, -1+) (0+, 0-)
1
P
(1-, 0+)
(1-, -1-)
3
P
(-1+, 0-) (-1-, 0+)
1
D , 3P
(-1-, 0-)
3
P
(-1+, -1-)
-2
1
D
O fato de existir ML  2 (ou ML  2 ) indica um termo do tipo D. Como na linha com ML  2
somente a casa com MS  0 está ocupada, isto mostra que o 1D é permitido enquanto que o 3D
não o é. Ora, um 1D tem 15 = 5 estados, cada um deles sendo dado por uma combinação linear
dos microestados em cada uma das cinco casas da coluna com MS  0 , respectivamente.
Portanto, este número (cinco) deve ser descontado dos nove microestados na coluna com
MS  0 . Passemos em seguida para a linha com ML  1 (ou ML  1 ). Este valor indica um
termo do tipo P, tendo em vista que os valores ML  2 ,  2 já foram utilizados. Como todas as
casas nesta linha estão ocupadas temos um 3P permitido. Como o 3P tem nove estados, este
número deve ser descontado do número de microestados contidos nas nove casas
correspondentes a ML  1 , 0 ,  1 e MS  1 , 0 ,  1 . Note que, com isto, os quatro microestados
nas casas com ML  1 ,  1 e MS  0 foram utilizadas para formar estados do 1D e do 3P, e,
portanto, o termo 1P não é permitido. Se os elétrons não fossem equivalentes isto não ocorreria,
como no caso da configuração excitada 1s12p1 do He. Finalmente, é fácil perceber que o termo
restante permitido é o 1S. O número total de estados  (2S+1)(2L+1) = 15, como era de se
esperar.
1.6 Operadores tensoriais irredutíveis
A álgebra de momento angular foi generalizada a partir de 1942 com os trabalhos de
Racah e Wigner, principalmente. Racah introduziu o conceito de operador tensorial irredutível e
desenvolveu métodos extremamente potentes e mais simples que os métodos anteriormente
conhecidos para o cálculo de elementos de matriz das interações em sistemas atômicos e
moleculares. A chamada álgebra de Racah, ou também álgebra de Racah-Wigner, foi
inicialmente desenvolvida com relação às propriedades de rotação de um sistema esférico, e,
portanto, com relação ao grupo contínuo R3 (grupo das rotações). Essa álgebra tem sido muito
utilizada em vários ramos da química e da física, como por exemplo, a espectroscopia, a química
teórica, a física atômica e molecular e a física nuclear e de partículas. Devemos salientar que a
teoria dos grupos desempenha um papel importantíssimo nessa álgebra, pois é capaz de
descrever todos os seus aspectos qualitativos.
Um tensor de ordem n é uma quantidade com n componentes, as quais mediante uma
rotação do sistema de coordenadas sofrem uma transformação linear. Os tensores ligados a um
mesmo sistema de coordenadas seguem uma álgebra cujas operações elementares são as
seguintes:
i) Adição
Sejam dois tensores de mesma ordem, a e b, os quais são submetidos à mesma
transformação linear induzida por uma rotação do sistema de coordenadas. As somas ai + bi de
componentes correspondentes constituem as componentes de um tensor, a saber, o tensor soma.
ii) Produto
Sejam dois tensores a e b com n e m componentes, respectivamente. Os nm produtos
aibj constituem as componentes de um novo tensor chamado de produto direto dos tensores
iniciais.
iii) Transformações lineares
Seja um tensor de ordem n e uma matriz T (n por n). As quantidades
b j   Tjia i
i
(1.6.1)
constituem também as componentes de um tensor de ordem n. Quando um tensor é submetido a
uma transformação, induzida por uma rotação do sistema de coordenadas, utilizamos a notação
b j   D jia i
(1.6.2)
i
onde de forma geral cada componente bj é uma combinação linear de todos os ai’s. Porém, é
possível se encontrar um novo conjunto de componentes { a r } ligado aos ai’s por uma certa
transformação linear
ar   A ri a i
(1.6.3)
i
de tal modo que mediante uma rotação do sistema de coordenadas certas partes do conjunto { a r }
se transformam separadamente. Isto significa que a matriz de rotação de { a r }, que é dada por
D  ADA1
(1.6.4)
é uma matriz na forma de blocos. Assim, para cada bloco temos que os bj ’s são expressos como
uma combinação linear dos a r ’s correspondentes. Vejamos o exemplo abaixo.

Sejam as três componentes, x, y e z, do vetor posição r . Estas componentes constituem
um tensor de ordem três, pois elas satisfazem as três propriedades mencionadas acima.
Consideremos uma rotação de um ângulo  em torno de z. A matriz que descreve esta rotação é
 cos  sen  0
D   sen  cos  0
 0
0
1
ou seja
(1.6.5)
 cos  sen  0  x  X 
 sen  cos  0  y   Y 

   
 0
0
1  z   Z 
(1.6.6)
onde X  x cos   y sen  , Y  x sen   y cos  e Z = z. Consideremos em seguida a
transformação
1  
3
( x  iy )
8
1 
3
( x  iy )
8
0 
3
z
4
(1.6.7)
ou seja
 x   1 
A  y   1 
 z   0 
(1.6.8)
onde a matriz A é dada por




A




3
8
3
8
0
3
8
3
i
8
i
0

0 


0 

3 
4 
e a sua inversa A-1 é dada por
(1.6.9)
 1 8

 2 3
 i 8
A 1  
2 3

 0


1 8
2 3
i 8
2 3
0

0 


0 

4 
3 
(1.6.10)
De acordo com a relação (1.6.4), a matriz de rotação do conjunto {  } é dada por
0
0 e i
cos   i sen 

D  ADA1  
0
cos   i sen  0   0

0
0
1  0
0
e i
0
0

0
1
(1.6.11)
Note, portanto, que a matriz D é mais “bloqueada” que a matriz D, ou seja, foi possível

encontrar um conjunto {  } que contem as mesmas informações físicas contidas em { r } mas
que se transforma, sob uma rotação do sistema de coordenadas, de modo mais simples e
conveniente. Note que D nos dá simplesmente
1  ei 1
1  ei1
(1.6.12)
0  0
De modo geral podemos sempre encontrar uma transformação que deixe a matriz
D ainda mais reduzida, ou seja, em blocos menores. Porém, esse processo tem um limite. Cada
bloco comporta-se separadamente de modo independente e corresponde a um subconjunto de
uma certa base de funções ou de operadores. Neste limite cada um desses subconjuntos
denomina-se um tensor irredutível. No conjunto {  } acima cada componente comporta-se
como um tensor irredutível sob uma rotação em torno de z. Porém, de modo genérico, para uma
rotação arbitrária do sistema de coordenadas em torno das três direções cada componente de { 
} é uma combinação linear das três componentes de {  }. Por isso, considera-se que o tensor
irredutível é o próprio conjunto {  }; um tensor irredutível de posto1 e ordem três, o qual é
designado por (1) .
As funções (m1) acima são na verdade um caso particular das funções
(ML)  r L YL, M
(1.6.13)
onde os YL,M são os conhecidos harmônicos esféricos. Se tivéssemos usado o procedimento do
exemplo acima com as nove componentes do tensor simétrico {xx , xy , ... , zz}, iríamos
encontrar uma matriz reduzida a três blocos, 55, 33 e 11, correspondendo aos tensores
irredutíveis ( 2) , (1) e ( 0) , respectivamente. Isto significa que o tensor {xx , xy , ... , zz} pode
ser decomposto, ou separado, nos tensores irredutíveis ( 2) , de posto 2 e ordem 5 (cinco
componentes), (1) , de posto 1 e ordem 3 (três componentes) e ( 0) , de posto 0 e ordem 1 (uma
componente).
Como a quantidade rL é invariante sob qualquer rotação do sistema de coordenadas,
podemos dizer que o tensor harmônico esférico Y(L) é um tensor irredutível de posto L e ordem
(2L+1) com componentes YM( L ) (-L  M  L ). As matrizes de transformação (rotação) dos
harmônicos esféricos são conhecidas como as matrizes de rotação de Wigner. Vamos assim
definir um tensor irredutível esférico de posto k e ordem (2k+1) como sendo uma
quantidade com (2k+1) componentes que, sob uma rotação do sistema de coordenadas, se
transforma como o harmônico esférico Y(k).
Podemos ir mais adiante e definir um operador tensorial irredutível esférico T(k), de
posto k e ordem (2k+1), como sendo uma quantidade que, mediante uma rotação do sistema de
coordenadas, satisfaz a condição
D̂Tq( k ) D̂1   D(qkq) Tq(k )
(1.6.14)
q
onde D̂ representa uma operação de rotação e os D(qkq) são os elementos da matriz de rotação de
Wigner (2k+1)(2k+1). Pode-se mostrar que os harmônicos esféricos satisfazem esta condição e,
portanto, podem também ser considerados como operadores tensoriais irredutíveis.
A partir de dois tensores irredutíveis, ou dois operadores tensoriais irredutíveis, de postos
k1 e k2, podemos formar os (2k1+ 1)(2k2+ 1) produtos Tq(1k1 )Tq( 2k 2 ) , os quais constituem as
componentes de um novo tensor (tensor produto). Porém, esse novo tensor não é
necessariamente irredutível. A pergunta que fazemos então é a seguinte: De que maneira
podemos combinar os (2k1+ 1)(2k2+ 1) produtos para formar um novo tensor irredutível ? A
resposta à essa pergunta pode ser facilmente dada se lembrarmos que os tensores irredutíveis
esféricos comportam-se como os harmônicos esféricos e, por conseguinte, como as autofunções
de momento angular. Assim sendo, a combinação linear dos produtos Tq(1k1 )Tq( 2k 2 ) que dá como
resultado um tensor irredutível esférico PQ( K ) é
PQ( K ) 

k1q1k 2q 2 k1k 2KQ Tq(1k1 )Tq( 2k 2 )
(1.6.15)
q1 , q 2
que é análoga à eq. (1.4.5). A notação comumente utilizada para representar o tensor irredutível
resultante é

PQ( K )  Tq(1k1 )Tq( 2k 2 )

(K)
Q
(1.6.16)
1.7 O teorema de Wigner-Eckart
Consideremos a eq. (1.4.5), ou a eq. (1.6.15), em termos de harmônicos esféricos Yk,q e
Y,m . Porém, consideremos Y,m como uma autofunção de momento angular e Yk,q como um
operador tensorial irredutível. A ação do operador Yq( k ) sobre uma autofunção  m produzirá
um estado que não é, obviamente, ortonormal ao espaço formado pelo conjunto {  m }, pois
 m não é autofunção de Yq( k ) . De acordo com a eq. (1.4.5), ou a eq. (1.6.15), temos
 L M   k q  m k  L M Yq( k )  m
q, m
(1.7.1)
onde  representa um conjunto de números quânticos que especificam o estado LM , ou seja,
eles indicam que esse estado provem da ação dos operadores Yq( k ) sobre as autofunções  m . Os
coeficientes de Clebsch-Gordan constituem uma transformação unitária. A transformação inversa
que corresponde à eq. (1.7.1) é dada por
Yq( k )  m   k  L M k q  m LM
(1.7.2)
L, M
Tomando o produto da equação acima por uma autofunção  m temos
 m Yq( k )  m   k  L M k q  m  m LM
(1.7.3)
L, M
No lado direito desta equação, o produto escalar  m L M é que contem a natureza do
operador que está atuando sobre as autofunções  m , já que as quantidades k  LM kq m são
coeficientes de Clebsch-Gordan. Além disso, como é um produto escalar entre duas autofunções
de momento angular, ele deve se anular para L   e/ou M m e não deve depender das
orientações dos momentos angulares especificados por L e  , ou seja, não deve depender de M e
m. Para representar este produto escalar usa-se a notação
 Y( k )  , que se denomina
elemento de matriz reduzido. Assim, o elemento de matriz na eq. (1.7.3) pode ser escrito como
 m Yq( k )  m  kqm km  Y( k ) 
(1.7.4)
o qual fica assim separado numa parte puramente geométrica (o coeficiente de Clebsch-Gordan),
que leva em conta as propriedades de rotação das autofunções  m e do operador Yq( k ) , e numa
parte puramente física que leva em conta a natureza deste operador.
Ao invés de trabalharmos com os coeficientes de Clebsch-Gordan, utilizaremos os
chamados símbolos 3-j , os quais são definidos do seguinte modo
j2
 j1

 m1 m2
j3 
  (1) j1  j2  m 3 (2 j3  1) 1 / 2 j1m1 j2 m2 j1 j2 j3  m3
m3 
(1.7.5)
O valor numérico de um símbolo 3-j não se altera mediante permutações cíclicas das colunas, ou
seja
j2
 j1

 m1 m2
j3   j3

m3   m3
j1
m1
j2   j2

m2   m2
j3
m3
j1 

m1 
(1.7.6)
Para permutações não cíclicas temos a seguinte relação
j2
 j
(1) j1  j2  j3  1
 m1 m2
j3   j2

m3   m2
j1
m1
j3   j1
j3
  
m3   m1 m2
j2   j3

m3   m3
j2
m2
j1 

m1 
(1.7.7)
A condição de ortonormalidade dos símbolos 3-j é dada por
 j1
j2
  m
m1 , m 2

1
m2
j3 

m3 
j2
 j1

 m1 m2
j3 
1
 
 j , j m , m
mm  (2 j3  1) 3 3 3 3
(1.7.8)
ou também
j2
 j1


m2
m1 , m 2 , m 3  m1
2
j3 
 1
m3 
(1.7.9)
As condições de não nulidade para estes símbolos são essencialmente as mesmas dos
coeficientes de Clebsch-Gordan, isto é, a condicão de triangularidade nos j’s e m1+ m2 + m3 = 0.
Outra relação importante envolvendo os símbolos 3-j, que na realidade corresponde à
transformação inversa (1.7.3), é a seguinte:
 (2 j
3
j3 , m 3
j2
 j
 1)  1
 m1 m2
j3 

m3 
j2
 j1

 m1 m2
j3 
  m1 , m1 m 2 , m2
m3 
(1.7.10)
O teorema de Wigner-Eckart para um operador tensorial irredutível atuando entre autofunções de
momento angular pode então ser colocado na seguinte forma (Edmonds 1957, Silver 1976,
Condon e Odabasi 1980, Judd 1998)
k J
 J
 J  T ( k ) J
J M Tq( k ) JM  (1) JM 
  M q M 
(1.7.11)
Note que dessa maneira alguns fatores de fase e o fator (2j3 + 1)-1/2 que relaciona os símbolos 3-j
com os coeficientes de Clebsch-Gordan, Eq. (1.7.5), foram incorporados ao elemento de matriz
reduzido. Podemos encontrar na literatura tabelas que fornecem os valores numéricos dos
símbolos 3-j, como por exemplo, as clássicas tabelas de Rotenberg et al. (1959).
No caso dos harmônicos esféricos utilizamos comumente os chamados operadores de
Racah, C(k), que são definidos por
 4 
C(qk )  

 2k  1 
1/ 2
Yq( k )
(1.7.12)
Utilizando a expressão
  k  
  C( k ) 
m C(qk ) m  (1)  m 

  m q m
(1.7.13)
dada pelo teorema de Wigner-Eckart, e a conhecida integral envolvendo três harmônicos
esféricos (integral de Gaunt)
Y

 , m 
 (2  1)(2k  1)(2  1) 
Yk , q Y, md  (1) 

4


1/ 2
m
podemos facilmente mostrar que
  k     k  

 

 0 0 0    m q m 
(1.7.14)
k 
1 / 2  

 C( k )   (1) (2  1)(2  1) 
 0 0 0
(1.7.15)
Satisfeita a condição de triangularidade, para que o símbolo 3-j que aparece na Eq. acima seja
diferente de zero é necessário que   k   seja par. Este fato tem uma grande importância,
como veremos ao longo desse texto, nas regras de seleção para elementos de matriz envolvendo
os operadores de Racah e autofunções de momento angular.
MÉTODOS PERTURBATIVOS.
2.1 O determinante secular
Na mecânica quântica sabemos que a equação de Schrödinger tem solução exata em
apenas alguns casos como, por exemplo, o átomo de hidrogênio e o oscilador harmônico. Em
particular, no caso de sistemas quânticos com mais de um elétron ela não tem solução exata.
Assim sendo, procura-se, na maioria dos casos, soluções aproximadas. Descreveremos neste
capítulo os métodos mais usuais de se encontrar estas soluções.
Consideremos um sistema quântico cujo hamiltoniano H pode ser separado em duas
partes, H0 e V, tal que
H  H0  V
(2.1.1)
Consideremos também que as autofunções de H0 são conhecidas (na prática, mesmo que de
forma aproximada), ou seja, assumiremos que o problema
H0 n  E n n
(2.1.2)
foi previamente resolvido e que o conjunto {n} é completo e ortonormalizado. Dessa forma
podemos procurar as autofunções de H através de combinações lineares no espaço formado pelas
autofunções n , isto é, podemos escrever
   c n n
(2.1.3)
n
onde  deve satisfazer a equação
H E 
(2.1.4)
a qual, utilizando-se as equações (2.1.1-3), pode ser colocada na forma
c E
n
n
n   cn V n   cn E n
n
n
(2.1.5)
n
Multiplicando-se a equação acima, da esquerda para a direita, por
m
(que é uma das
autofunções do conjunto {n}) encontramos
c E
n
n
m n   cn m V n   cn E m n
n
n
(2.1.6)
n
Como m n  mn , a equação (2.1.6) pode ser reescrita como
c   E 
n
n mn
 Vmn   E mn   0
(2.1.7)
n
onde usamos a notação m V n  Vmn . Assim, para cada autofunção m escolhida teremos
uma equação do tipo (2.1.7). Se o nosso conjunto {n} é formado por N autofunções n (em
princípio N é infinito) podemos construir N equações do tipo (2.1.7), formando um sistema
homogêneo (o lado direito das equações é igual a zero) onde as incógnitas são os cn’s. Como o
sistema de equações é homogêneo, para que tenhamos uma solução que não seja a solução trivial
(todos os cn’s = 0) é necessário que o determinante formado pelos coeficientes dos cn’s seja igual
a zero, isto é
 Enmn  Vmn   E mn
0
(2.1.8)
Este é o chamado determinante secular, o qual, conhecendo-se os autovalores En na equação
(2.1.2) e os elementos de matriz Vmn , permite determinar os possíveis valores de E, ou seja, os
autovalores de H. O determinante secular tem dimensão NN. Como na prática não podemos
considerar N = , normalmente fazemos uma truncagem que é regida pelas características das
propriedades do sistema quântico sob estudo. Você pode, portanto, notar que quanto maior for a
dimensão do determinante secular mais corretos serão os autovalores E. De modo mais explícito
o determinante tem a seguinte forma
E1  V11   E
V12

V1N

V2 N

V21
E 2  V22   E



VN1
VN 2

0
(2.1.9)
E N  VNN   E
Note que os autovalores En e E só aparecem na diagonal principal. A equação (2.1.9) é, na
realidade, uma equação de grau N em E e, portanto, tem N raízes que são os possíveis valores de
E (autovalores de H). Com os recursos computacionais disponíveis hoje em dia pode-se resolver
determinantes seculares de dimensões enormes. Os coeficientes cn , para cada possível valor de
E, podem ser determinados escolhendo-se (N-1) das N equações do tipo (2.1.7) juntamente com
a condição de normalização
N

n 1
2
cn  1
(2.1.10)
Encontrando-se os cn’s para um dado E, tem-se a respectiva autofunção  .
Uma importante interpretação associada a este procedimento é dada a seguir. Dizemos
que o hamiltoniano H0 é diagonal com relação à base formada pelas autofunções n , ou seja,
se pensássemos num determinante secular envolvendo apenas H0 só apareceriam elementos não
nulos na diagonal principal e os autovalores seriam os próprios En, dado que a equação (2.1.2) é
satisfeita. O mesmo vale para H com relação às autofunções  . Porém, H não é diagonal com
relação à base formada pelas autofunções n , como mostra o determinante secular (2.1.9).
Dizemos que a interação V conecta diferentes n ’s, ou também, através de V as autofunções
n se misturam.
O método do determinante secular é o procedimento mais genérico e usual para se
encontrar autofunções e autovalores de um dado hamiltoniano que pode ser separado de acordo
com a equação (2.1.1). Ele é comumente utilizado na descrição de sistemas quânticos na física e
na química.
2.2 Teoria das perturbações independentes do tempo
Uma forma alternativa de se encontrar autofunções e autovalores aproximados de um
certo hamiltoniano pode ser utilizada quando na equação (2.1.1) a interação V, considerada aqui
como não dependente do tempo, é bem menor que H0. Este procedimento constitui a chamada
teoria das perturbações independentes do tempo. A interação V é tratada como uma perturbação
que é adicionada a H0 no sistema quântico.
Pode-se mostrar que (veja, por exemplo, A.S. Davydov : Quantum Mechanics ,
Pergamon Press) a correção até primeira ordem para a função de onda do m-ésimo estado do
sistema quântico é dada por
 m  m  
nm
Vnm
n
Em  En
(2.2.1)
onde os ’s e E’s representam as autofunções e autovalores que satisfazem a equação (2.1.2), ou
seja, as autofunções e autovalores do hamiltoniano não perturbado (H0). Também pode-se
mostrar que a correção até segunda ordem para a respectiva energia é dada por
 m  E m  Vmm  
nm
Vnm
2
Em  En
(2.2.2)
A condição de aplicabilidade para as equações acima é
Vnm  Em  En
(2.2.3)