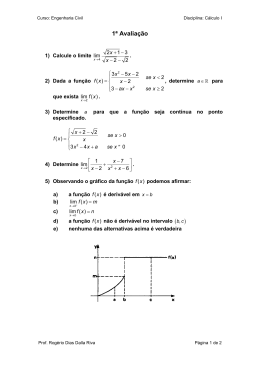
Lista de Exercícios Sobre Sequências e Séries
1. Mostre que {xn = cos(πn)} nao tem limite.
2. Enuncie e demonstre o Teorema de Sanduiche para sequências.
√
√
3. Mostre que as seqüencias { n n} e { n a} com a > 0 convergem para 1.
√
n
4. Mostre que lim n! = ∞
n→∞
5. Determine os quatro primeiros termos de cada seqüência, analise a sua convergência e encontre o limite
caso exista:
n√ o
n
sen(2n+1)+n
n2
en +n2
a) an = n+2
, b) xn = (−1)n+1 en , c) b = n!n , d) yn = (−1)
2n+1
(2n)! , e) cn = e2n −2n , f) tn =
6. Seja a seqüência definida pela recorrência
(
x0 = 1
xn+1 =
sitivo, encontre o seu limite.
x2n +3
2xn
. Sabendo que ele converge para valor po-
7. Verifique a convergência das seguintes séries
∞
∞
X
X
n
P (−1)n (n+1)
P 2n+1
P 2+cos n
P
P cos n
cos(nπ)
1
√ , (c)
√ ,
(a)
, (b)
, (e)
, (f) 1+(−1)
, (g)
3
n
nn , (d)
n
n2
42n
n
n
n=1
k=2
∞
X
P n
P n!
(h) 2n! , (i)
(−1)n n+1
, (j)
nn
n2
n=5
8. Podemos aplicar o teste da razão no ítem (f) da questão acima? Justifique.
9. Analise a convergência das seguintes séries através do teste da raiz ou do teste da integral.
∞
X
P
P (−1)n n
P
n+1
(a) n12 ,
(d)
(b) (2n)n ,
(c)
n! ,
(2n)n
k=0
10. Obtenha o valor, usando séries geométricas:
∞
X
2n−7
(a)
π 21
,
(b) 2.5 31 31 . . .
n=3
11. Mostre que, se 0 < a0 ≤ a1 ≤ a2 ≤ a3 ≤ · · · então a séries alternada
∞
X
(−1)n ai diverge.
n=0
12. Mostre que a séries harmônica alternada
∞
X
(−1)n+1
n
converge e estime o valor com erro máximo de 0.2.
n=1
13. Encontre o centro e o raio de convergência das séries de potências
X en
P
√
a) (−1)n nxn
b)
xn
n!
14. Determine o intervalo de convergência
X 1
P
a)
n!xn
b)
xn
n!
c)
X n3
(x − 2)n
n+1
c)
X en
√ 3n−5
(x
−
3)
22n
d)
X ln n
2n
(x −
√
2)n
15. Encontre a série de potência de
(a) arctan(x2 ), sabendo que arctan0 (x) =
(b) arcsenx, usando arcsen0 x =
√ 1
1−x2
1
.
1+x2
2 k(k−1(k−2) x3 +· · ·
e a série binomial (1+x)k = 1+kx+ k(k−1)
2! x +
3!
+ k(k−1(k−2)
x3 + · · ·
3!
Rx
2
17. Encontre a série de Maclaurin de f (x) = 0 e−t dt.
16. Mostre que (1 + x)k = 1 + kx +
k(k−1) 2
2! x
18. Mostre que a função f (x) = senx pode ser representado como série de Taylor em torno de
x.
π
2 para
todo
19. Seja f (x) =
1
(2−x)3
(a) Encontre a Série de Maclaurin de f (sem usar a série binomial) e mostre que a série representa a
função em [−1, 1].
Z 1
1
dx
(b) Usando a série obtida acima, encontre a expressão de
3
−1 (2 − x)
20. Encontre a série de Taylor de cos x em torno de
π
2.
21. Encontre a representação
em série de potências e determine o seu raio de convergência
√
1
1
a) ln 2 + 3x
b) f ( x) onde (0) = 1, (f 0 (0) = 0 e f 00 (x) = 1+x
4
22. Verifique a convergência das séries
P (−1)n
a)
en
b)
X senn + cos n
2
n2
23. Encontre o centro e o raio de convergência das series de potencias
X n2n
X
n
a)
x
b)
e−n (x − 3)2n
(n!)n
24. Encontre o limite da seqüência convergente an tal que a0 = 1 e an+1 = an +
Entregar seguintes exercícios resolvidos da lista ou do livro até P1:
• Um sobre sequências.
• Um sobre séries geométrica.
• Um sobre séries alternada que envolve estimativa de erros.
• Um sobre teste da raiz ou da razão.
• Um sobre séries de potências para obter raio e intervalo de convergências.
• Um sobre séries de potências que representa a função conhecida.
• Mais dois a sua escolha.
1
2n+1
para n > 1.
Respostas e dicas
1. Use a subsequencia.
2. Reescreva o que foi feito na aula ou no livro.
3. Use a função ln
n
4. Dica: n! ≥ n2 2
1
5. a) lim an = ∞, b) lim xn = @, c) lim bn = 0, d) lim yn = 0, e) lim cn = 0, f) lim tn = .
n→∞
n→∞
n→∞
n→∞
n→∞
n→∞
2
√
6. lim xn = 3. Dica: Chame o limite de L e aplique o limite na fórmula de recorrência.
n→∞
7. (a), (b) e (e) divergem. (c), (d), (f), (g), (h) e (j) convergem absolutamente. (i) converge condicionalmente.
8. Não. Porquê?
9. (a), (c) e (d) convergem, (b) diverge
10. (a) é
8π
3
(b) é
25
10
+
31
990
=
2506
990 .
Dica: 2.5 31 31 . . . = 2.5 + 0.031 + 0.00031 + · · ·
11. Dica: mostre que lim |an | =
6 0
n→∞
12. Terá que somar até n = 5. O valor aproximado é
13. Sendo c o centro e R o raio, será
47
60 .
a) c = 0, R = 1,
√
√
14. a) @, b) I = R, c) I = (1, 3), d) I =
2 − 2, 2 + 2
b) c = 0, R = ∞,
c) c =
√
3, R =
q
3
4
e
15. a) arctan x é a soma da série de potências. Integrando, teremos a série de arctan x. Substitua o x2
nesta série.
b) Integrando a serie binomial que representa o arcsen0 x, teremos o arcsenx.
16. Use a série de Maclaurin.
17. Obter a séries de Maclaurin diretamente não é fácil. Encontre a séries de Maclaurin de et e partir dele,
2
obtenha a series de e−t e calcule a integral.
18. Mostre que todas derivadas são limitadas.
∞
X
(−1)n (n + 2)(n + 1)
f (n+1) (ξ )xn+1 n
19. a) f (x) =
xn , mostre que lim = 0 para |x| < 1. Depois
n+3
n→∞ 2×2
(n + 1)!
n=0
mostre que a séries converge para |x| = 1 e use o Teorema de Abel (a séries de potências é contínua o
intervalo de convergência).
Z 1
∞
∞
X
(−1)n (n + 2) X (n + 2)
b)
f (x)dx =
+
2 × 2n+3
2 × 2n+3
−1
n=0
20.
∞
X
n=0
21.
n=0
(−1)n π 2n+1
x−
(2n + 1)!
2
a)
∞
X
n n+1 n
(−1) 6
n=0
x , raio =
1
6
∞
X
(−1)n+1 xn
b) 1 +
,r=1
2n(2n − 1)
n=1
22. Todas convergem.
23. a) raio = ∞, b) raio =
1
e
n i
X
1 1
24. lim an = 2. Dica: Mostre que an =
(aplicar limite em ambos lados da relação de recorn→∞
2 2
i=0
rência não resolve).