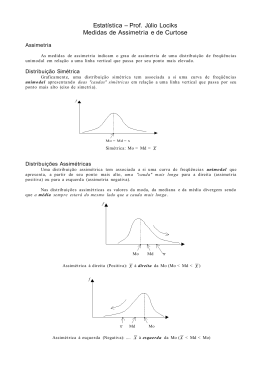
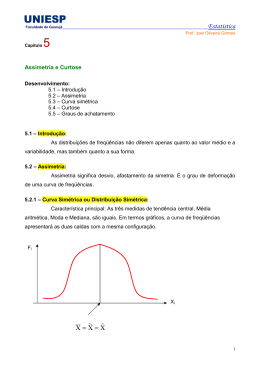
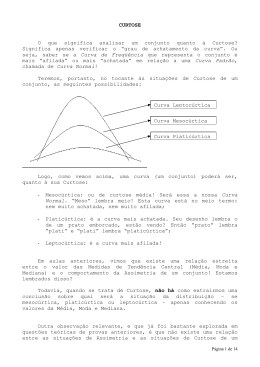
A NORMALIZAÇÃO DE DISTRIBUIÇÕES NÃO-NORMAIS
ATRAVÉS DA TRANSFORMAÇÃO DE BOX-COX E ALGUNS
COMENTÁRIOS SOBRE A AVALIAÇÃO DE QUALIDADE
André Luís Meira de Oliveira
Acadêmico - Engenharia de Produção e Sistemas
Universidade Federal de Santa Catarina
Clarice Castro Souza
Acadêmico, Engenharia de Produção e Sistemas
Universidade Federal de Santa Catarina
Patrick Boehme
Acadêmico, Engenharia de Produção e Sistemas
Universidade Federal de Santa Catarina
Robert Wayne Samohyl, Ph. D.
Professor titular, Universidade Federal de Santa Catarina
Departamento de Engenharia de Produção e Sistemas - Centro Tecnológico
e-mail: [email protected]
One of the most frequently used assumptions in Statistical Process Control is that
measurable variables follow the normal distribution. Traditional texts in the area discuss the
necessity of testing the null hypothesis of normality (for example, Besterfield (1995), Mittag e
Rinne (1993)), but do not explain what to do in the eventuality of rejection of the hypothesis.
In the literature, the normaliity assumption has been investigated in several works in terms of
process capacity indexes. Two of the most recent works suggest the use of generalized
distributions which include the normal as a special case. Castaglioli (1996), who offers a
broad bibliography of the literature, sugests using Burr distributions and Clements(1989) the
family of Pearson ditributions. In this paper, we propose to attack the problem of nonlinearity by transforming the original data through the Box-Cox (1964) transformation. The
transformation is programmed into an exceptionally easy to use procedure in EXCEL and
VISUAL BASIC which calculates the best possible transformation which minimizes the
presence of skewness and assymetry.
Key words: transformation; normality; quality.
1. Introdução:
Uma das suposições mais freqüentes na área de controle estatístico de processo é que
variáveis mensuráveis seguem distribuição normal. Manuais tradicionais vão até o ponto de
admitir que existe a necessidade de testar a hipótese nula de normalidade (por exemplo,
Besterfield (1995), Mittag e Rinne (1993)), mas não explicam o que fazer na eventualidade de
rejeição da hipótese. Na literatura, a suposição de normalidade tem sido investigada em vários
estudos no tocante a índices de capacidade de processo. Dois trabalhos mais recentes sugerem
o uso de distribuições de probabilidade mais gerais as quais incluem a distribuição normal
como um caso especial. Castagliola (1996) sugere o uso de distribuições de Burr e Clements
(1989) a família de distribuições Pearson. O primeiro trabalho oferece uma curta mais
abrangente bibliografia da literatura. Neste trabalho nos propomos a atacar o problema de nãonormalidade pela transformação dos dados originais através da transformação Box-Cox para
chegar a valores transformados que demonstrem normalidade ou no mínimo normalidade
aproximada. Mostraremos também uma rotina no ambiente EXCEL e VISUAL BASIC que
calcula a melhor transformação possível para alcançar valores mínimos para medidas de
assimetria e curtose, assim eliminando a não-normalidade.
A transformação BOX-COX foi introduzida na literatura em 1964 para resolver o
problema de estimação de regressões não lineares. Veja Kennedy, 1994, pp. 103-104, onde
existe um resumo desta área de Econometria. Box e Jenkins usam esta transformação no
software Autobox (1990) para calcular variâncias estáveis.
2. A transformação BOX-COX:
A transformação é relativamente simples:
y(λ) =
(y
λ
− 1)
λ
Onde λ varia entre (-1,1). O valor transformado dos dados passa através de
vários tipos de equações para cada valor de λ. Veja a tabela 1 a seguir:
se λ for
igual a:
-1,0
-0,5
0,0
0,5
1,0
yλ − 1
será igual a:
λ
1
+1
y
1
−1
y
− 0,5
ln y (da regra de L’Hospital)
y −1
0,5
y-1
então
Tabela 1.Alguns valores transformados, para determinados valores de λ.
O resultado do que y ( 0 ) = ln y pode ser demonstrado utilizando a regra de L’Hospital.
Portanto, medidas de assimetria e curtose são minimizadas e a distribuição normal aproximada
quando valores apropriados de λ são encontrados. O coeficiente de assimetria é definido como:
m3
σ3
coef. de assim =
Onde m3 é o terceiro momento de distribuição e σ 3 é o desvio padrão elevado ao
cubo. Existe uma relação entre λ e o coeficiente de assimetria representado no gráfico 1.
Assimetria
BJ
Curtose
.
.
5,99
.
A
B
C
λ
Gráfico 1. A relação entre λ e algumas medidas da não normalidade.
No ponto A, assimetria está no seu valor mínimo dado o valor apropriado de λ.
O coeficiente de curtose é medido pelo quarto momento normalizado pelo desvio
padrão elevado a quatro.
coef. de curtose =
m4
σ4
Desde que o coeficiente de curtose em excesso apresentado é igual a três no caso da
distribuição normal, nesse trabalho utilizaremos o coeficiente de curtose em excesso:
 m4 
coef. de curtose em excesso =  4 − 3

σ
Existe uma relação entre λ e o coeficiente de curtose em excesso representada no
gráfico 1. No ponto C, curtose é minimizado.
A estatística de Bera-Jarque segue a distribuição normal de χ 2 sob hipótese nula de
normalidade com dois graus de liberdade e é uma média ponderada dos dois coeficientes
apresentados acima:
  m3 2  m4  2 
 3
 4 − 3 
σ 
σ
 

2
BJ = N* 
+
 ≈ χ(2)
6
24




Onde N é o tamanho da amostra e num nível de significância de 5% o valor de χ (22 ) =
5,99. Em outras palavras, quando BJ é menor do que 5,99, a hipótese nula de normalidade é
aceita. O gráfico 1 demonstra também a relação entre λ e a estatística de Bera-Jarque. No
ponto B a estatística tem valor mínimo e talvez menor que 5,99.
3. Os cálculos no ambiente EXCEL:
O programa foi desenvolvido no ambiente EXCEL-VISUAL BASIC utilizando a
transformação BOX-COX para a normalização de amostras que não apresentam distribuição
normal, através do cálculo dos valores mínimos de assimetria e curtose.
O usuário insere em um quadro a amostra a ser analisada, essa amostra poderá
apresentar até quinhentos elementos. O intervalo de variação de λ é de (-5,5).
Feito isto o programa efetuará os cálculos da função Y transformada, dos
coeficientes de assimetria e curtose, além dos cálculos da função Bera-Jarque. Analisando os
valores obtidos nesta última função o programa oferecerá ao usuário o melhor vetor da função
Y transformada, ou seja, aquele que melhor satisfaz a condição para a eliminação da não
normalidade, onde χ 2 ≈ 0 .Também será fornecido ao usuário o melhor valor de λ e um
gráfico com os valores da estatística de Bera-Jarque e dos coeficientes de assimetria e de
curtose em função da variável λ.
4. Exemplo:
Submetemos o programa a um exemplo, os valores do vetor não transformado segue
a seguinte distribuição:
Gráfico 2. Histograma da amostra a ser transformada.
Após a efetuados os cálculos, tem-se o melhor λ, igual a -1,8. No gráfico 3 podemos
observar a distribuição após a transformação.
Gráfico 3.Histograma da amostra após a transformação.
σ2
Gráfico 4. Distribuições dos coeficientes de Assimetria, Curtose e da Estatística de BeraJarque, em função de λ.
5. Comentários:
Existem pelo menos dois casos importantes na área de Controle de Qualidade onde a
transformação de Box-Cox pode ser utilizada com freqüência: para o cálculo de índices de
capacidade de processo e na montagem de gráficos de controle. Muitas vezes na distribuição
os dados da linha de produção não são normais, e isso implica em valores diferentes para
índices acima e abaixo da média. Assim, há uma necessidade de falar em Cpk dividido em Cpu
e Cpl. O menor valor de Cpk é o escolhido para representar a capacidade do processo.
Clements (1989) oferece uma metodologia para o cálculo de Cpk na presença de nãonormalidade que leva em conta explicitamente medidas de assimetria e curtose na distribuição
de Pearson. O procedimento sugerido em nosso trabalho é o seguinte:
1. Com os dados originais, calcular o valor de assimetria e curtose e
subseqüentemente o valor da estatística de Bera-Jarque.
2. Se o valor de Bera-Jarque fosse menor que 5,99, então os dados são normais e
nenhuma transformação é necessária.
3. Se o valor de Bera-Jarque fosse maior de 5,99, então os dados não seguem a
distribuição normal e precisam ser transformados. Aplicar a transformação de Box-Cox.
4. Com os dados transformados, calcular o índice de capacidade de processo Cpk.
Neste caso, em função da transformação que normalizou os dados, o Cpk é simétrico (Cpu =
Cpl).
O procedimento para a montagem de gráficos de controle é muito parecido. Passos
1, 2, e 3 são idênticos. Se não houver rejeição da hipótese de normalidade, os gráficos podem
ser montados regularmente. Se rejeitar a hipótese, os dados deveram ser transformados. Passo
4 entraria com a montagem do gráfico utilizando os dados transformados e posteriormente
cada vez que um novo ponto está acrescentado no gráfico ele terá’ que sofrer a transformação
com a variável λ apropriado.
6. Conclusões:
A suposição de normalidade é tradicional na estatística, e experiência mostra que na
maioria dos casos nenhum prejuízo ocorre quando a suposição é utilizada para investigações
preliminares de dados. No evento de que uma empresa esteja implantando para a primeira vez
estatística de processo na fábrica, nestas fases iniciais, a suposição de normalidade é
considerada adequada e freqüentemente nem discutida. Uma empresa experimentando pela
primeira vez com procedimentos estatísticos na fábrica certamente sentirá uma diferença na
eficiência desta, com ou sem levar em conta normalidade nos dados. No entanto, no decorrer
do tempo e da aprendizagem, a empresa poderia avançar para níveis de eficiência maior,
modificando aos poucos os procedimentos e incorporando um nível de sofisticação maior. Na
segunda fase de melhorias deve ser contemplada então, a utilização da transformação de BoxCox. A metodologia apresentada neste trabalho está em fase de teste em várias empresas de
Santa Catarina e pelo menos neste momento preliminar a sua aplicabilidade tem mostrado
resultados interessantes.
6. Bibliografia:
AutoBox Plus. AFS, Inc., 1990.
BESTERFIELD, Dale H. Control de calidad. México, cuarta edicion, Prentice and Hall,
1995.
BOX, G. E. P. e COX, D. R. An analisis of transformatios. Jornal of the Royal Statistical
Society, series B, 26, 211-243.
CLEMENTS, John. Process capability calculations for non-normal distributions. Jornal of
quality process, 95-101, setembro,1989.
KENNEDY, Peter. A guide to econometrics. Massachusetts, third ediction, The mit press,
1992.
MITTAG, H. J. e RINNE, H. Statistical methods of quality assurance. London, Chapman and
Hall, 1993.