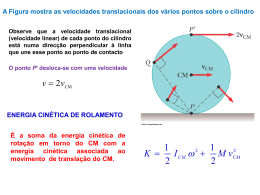
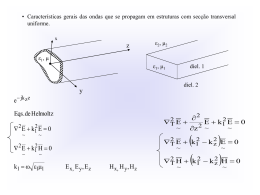
CONVERSÃO MATRICIAL DE SEGMENTOS DE RETA
ATRIBUTOS DESEJÁVEIS
•
•
•
•
•
Linearidade: o arranjo dos pixels devem dar a aparência
de estarem todos sobre um segmento de reta
Intensidade ou espessura uniforme: a imagem do
segmento não varia de extensão ao longo da sua
extensão
Continuidade: sem interrupções
Precisão: a imagem inicia-se e termina nos pontos
especificados
Intensidade independente da inclinação: segmentos de
diferentes inclinações possuem imagens de mesma
intensidade
CONVERSÃO MATRICIAL DE SEGMENTOS DE RETA
ALGORITMO 1
var
x,y,x1,x2, y1, y2: inteiro;
a: real;
begin
a := (y2-y1) / (x2-x1);
for x := x1 to x2 do begin
y := round ( y1 + a * (x2 – x1));
PintaPixel (x,y);
end;
end;
CONVERSÃO MATRICIAL DE SEGMENTOS DE RETA
ALGORITMO BRESENHAM (1965)
var
x, y, x1, x2, y1, y2, s: inteiro;
y := y1;
dy := 2*(y2 – y1);
dx := - 2*(x2 – x1);
s := -(x2-x1) + dy;
for x := x1 to x2 do begin
PintaPixel (x,y);
if s > 0 then begin
s := s + dx + dy;
y := y+1;
end;
else s := s + dy;
end;
TRANSFORMAÇÕES BIDIMENSIONAIS
Dois aspectos da formulação das transformações devem ser enfatizados:
1) Uma transformação é uma entidade matemática única e, como tal, pode ser
denotada por um único nome ou símbolo;
2) Duas transformações podem ser combinadas, ou concatenadas, para a obtenção
de uma única transformação que tenha os mesmos efeitos obtidos pela aplicação
sequencial das duas originais. Assim, a transformação A poderia ser uma translação e
a transformação B uma
mudança de escala. A propriedade de concatenação nos permite determinar uma
transformação C=AB, cujo efeito é transladar e então escalar o objeto.
TRANSFORMAÇÕES BIDIMENSIONAIS
Os princípios de denotação e concatenação irão
pertencer a todas as transformações descritas : recorte
(clipping), apresentação em janela (windowing) e
transformações tri-dimensionais e de perspectiva. Cada
uma destas transformações é usada para gerar um novo
ponto (x’, y’) a partir das coordenadas de um ponto (x, y)
proveniente da descrição da figura original. Se a definição
original inclui uma linha, é suficiente aplicar a
transformação aos pontos da extremidade e mostrar a
linha entre os dois pontos transformados.
TRANSFORMAÇÕES BIDIMENSIONAIS
-
A forma da transformação de
translação é:
x’ = x + Tx
y’ = y + Ty
TRANSLAÇÃO
TRANSFORMAÇÕES BIDIMENSIONAIS
Rotação
Para rodar um ponto (x, y) de um ângulo  em sentido horário, em torno da origem do
sistema de coordenadas, devemos escrever:
x’ = x cos  + y sin 
y’ = -x sin  + y cos 
O triângulo (20, 0), (60, 0), (40, 100) rotacionado 45 (sentido horário) em torno da
origem é (14.14, -14.14), (42.43, -42.43), (98.99, 42.43), e está mostrado na
figura 2. Estas equações podem ser usadas somente se a rotação é em torno
da origem do sistema de coordenadas.
TRANSFORMAÇÕES BIDIMENSIONAIS
Figura 2 - Rotação em torno da origem
TRANSFORMAÇÕES BIDIMENSIONAIS – MUDANÇA DE ESCALA
As transformações de escala
x’ = xS
x
y’ = ySy
podem ser usadas para diversos fins. Se a figura
deve ser ampliada para duas vezes o seu
tamanho original, nós devemos escolher
Sx = Sy = 2. Note que a ampliação é
relativa à origem do sistema de
coordenadas. O triângulo (20, 0), (60, 0),
(40, 100) passa a ser (40, 0), (120, 0), (80,
200), como mostrado na figura 3.
Figura 3 - Mudança de
Escala em relação à origem
TRANSFORMAÇÕES BIDIMENSIONAIS
Figura 6 - Ordem diferente de transformações
TRANSFORMAÇÕES BIDIMENSIONAIS – FORMULAÇÃO MATRICIAL
x'
y ' 1  x
a

y 1b
 c
d
e
f
0

0
1
FORMULAÇÃO MATRICIAL– TRANSLAÇÃO
x'
y ' 1  x
1

y 1 0
Tx

0
1
Ty
0

0
1
FORMULAÇÃO MATRICIAL – ROTAÇÃO
 x'
 
y' 1  x
cos

y 1  sin 
 0

 sin 
cos
0
0

0
1
FORMULAÇÃO MATRICIAL – MUDANÇA DE ESCALA
 x'
 
y' 1  x
S x

y 10
 0

0
Sy
0
0

0
1
CONCATENAÇÃO DE TRANSFORMAÇÕES MATRICIAIS
Supondo-se que:
 x'
y' 1  x
2 0 0


y 1 0 2 0
0 0 1
 
 1 0 0


y  1  0 1 0
10 0 1
 

E que:
 x 
y  1  x 

CONCATENAÇÃO DE TRANSFORMAÇÕES MATRICIAIS
Portanto:
 x 
 
y  1  x
2 0 0  1 0 0



y 1 0 2 0  0 1 0
0 0 1 10 0 1

RESULTANDO:
 x 
 
y  1  x
 2 0 0


y 1  0 2 0
10 0 1

TRANSFORMAÇÕES COMPLEXAS
A transformação de rotação pode ser aplicada para rodar pontos somente em torno da
origem. Portanto, se desejamos derivar uma transformação que irá rodar um ponto de um
ângulo Ø em torno do ponto (Rx, Ry), primeiro precisamos transladar os pontos de tal forma
que (Rx, Ry) coincida com a origem.
x'
y ' 1  x
 1

y 1 0
  Rx

0
1
 Ry
0

0
1
Então a rotação pode ser aplicada
x
y 1  x
cos
y 1 sin
 0
 sin
cos
0
0
0
1
TRANSFORMAÇÕES COMPLEXAS
E finalmente, transladamos o ponto de tal forma que a origem retorne
para (Rx, Ry):
x
y 1  x
1

y 1 0
 Rx

0
1
Ry
0

0
1
TRANSFORMAÇÕES BIDIMENSIONAIS
Estas transformações podem ser concatenadas
 x 
 
y  1  x
 1

y 1 0
 R
 x

0
1
 Ry
0 cos

0  sin 
1  0
 sin 
cos
0
0  1

0  0
1  Rx
0
1
Ry
Se os valores de Rx, Ry e Ø forem conhecidos, as três matrizes
podem ser multiplicadas para se tornar uma só matriz de
transformação.
0

0
1
CONVERSÃO MATRICIAL DE SEGMENTOS DE RETA (EXERCÍCIOS)
1.
Descreva um algoritmo para encontrar os parâmetros da matriz de escalamento (e se
necessário, os parâmetro da matriz de rotação) para uma figura que será desenhada sobre
uma superfície retangular (folha de papel, tela, etc.) visando normalizá-la para ocupar o
máximo espaço desta superfície, sem deformá-la. O algoritmo deve prever o caso, da
figura necessitar sofrer uma rotação visando otimizar o preenchimento da superfície. A
figura encontra-se armazenada através das coordenadas absolutas de suas primitivas
sendo que, no início do arquivo encontram-se armazenados os valores de Xmin, Ymin,
Xmax e Ymax que correspondem respectivamente à menor abscissa, menor ordenada,
maior abscissa e maior ordenada da figura. Também, como entrada para este algoritmo
considere a superfície com diagonal nos pontos (0,0) e (Xs, Ys). Para cada uma das
transformações utilizadas no algoritmo, descrever seus parâmetros.
1.
Suponha que conheçamos um ponto (x’ , y’) e o fato de ele ser a transformação de um
ponto desconhecido (x , y), transformado pela matriz Q. Descreva um mecanismo para
encontrar o ponto original (x,y) . Para que área da computação gráfica este algoritmo
poderia ser útil ?
CONVERSÃO MATRICIAL DE SEGMENTOS DE RETA (EXERCÍCIOS)
3. Prove a afirmação de que a transformação de uma linha entre dois pontos A e B é equivalente à
linha entre os pontos gerados pelas transformações do ponto A e a transformação do ponto
B. Considere apenas as transformações de translação, rotação e mudança de escala.
4. A formulação matricial sugere outras transformações que nós não consideramos, por exemplo, a
transformação x’ = x + ay e y’ = y. Você é capaz de caracterizar estas transformações?