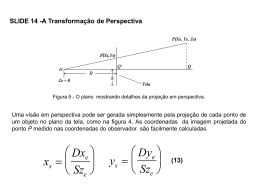
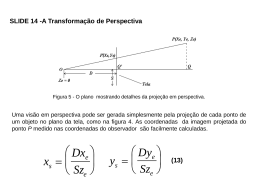
SLIDE 1 – Transformações - Translação
A transformação que translada um ponto para um novo ponto é:
 x
y z 1   x
1
0
y z 1
0
T
 x
0
1
0
Ty
0
0
1
Tz
0

0

0
1
onde , e são os componentes da translação nas direções x, y e z, respectivamente.
(1)
SLIDE 2 – Transformações – Rotação
Em três dimensões, é bastante útil projetar transformações de rotação em torno de cada um
dos três eixos coordenados, como mostrado abaixo:
Figura 1 - As três rotações tridimensionais primitivas. Ângulos são medidos em sentido
horário quando olhamos na direção do eixo de rotação, através da origem.
SLIDE 3 – Transformações
Rotação de um ângulo , em torno do eixo z (Figura 1a), é obtida
transformação:
 x
y z 1   x
 cos
 sin
y z 1
 0
 0
sin
cos
0
0
0
0
1
0
com a seguinte
0
0

0
1
(2)
SLIDE 4 – Transformações
Rotação de um ângulo , em torno do eixo coordenado y (Figura 1b) é dado por:
x
y z 1  x
y
 cos
 0
z 1
 sin

 0
0 sin
1
0
0 cos
0
0
0
0
0

1
(3)
SLIDE 5 – Transformações
Rotação de um ângulo , em torno do eixo coordenado x (Figura 1c) é realizada por:
 x
y z 1   x
0
1
0 cos 
y z 1
0 sin
0
0
0
 sin
cos 
0
0
0

0
1
(4)
SLIDE 6 – Transformações – Mudança de Escala
Uma transformação de Mudança de Escala pode ser usada para escalar dimensões em cada
direção coordenada separadamente:
 x
y z 1   x
 Sx
0
y z 1
0
 0
0
Sy
0
0
0
0
Sz
0
0
0

0
1
(5)
SLIDE 7- Transformações Inversas
A maioria das transformações dadas acima têm inversa, que realiza a transformação
simetricamente oposta. A inversa da matriz de translação é
 x y z 1   x
 1
 0
y z 1
 0
 T
x
0
1
0
Ty
0
0
1
Tz
0
0

0
1
(6)
que desfaz o efeito da translação da equação dada anteriormente. A inversa da primeira
matriz de rotação mostrada (rotação de em torno de z) é, simplesmente:
 cos 
 sin  

 0
 0
sin  
cos 
0
0
0 0
0 0

1 0
0 1
(7)
que é uma rotação de mesma magnitude, em torno do mesmo eixo, mas na direção oposta.
SLIDE 8 - Concatenação
A aplicação sucessiva de várias transformações sucessivas pode ser resumida em uma simples matriz de
transformação, a concatenação da seqüência. Suponha que duas transformações T1 e T2 tenham que ser
aplicadas sucessivamente. O mesmo efeito pode ser obtido com a aplicação de uma única transformação
T3, que é simplesmente o produto das matrizes T1 e T2. Isto pode ser prontamente demonstrado: o ponto
é transformado em por T1:
 x
y z 1   x
y z 1 T1
(8)
O ponto é então gerado pela aplicação de T2:
 x
y z 1   x y z 1 T2
(9)
Substituindo uma equação na outra, temos:
 x


y z 1   x y z 1 T1 T2   x y z 1  T1T2 
(10)
A ordem de aplicação das transformações deve ser preservada quando as
matrizes de transformação são unidas pela multiplicação.
SLIDE 9 - Transformações em Modelamento
Figura 2 - Modelamento de um automóvel pela instanciação
de símbolos e transformações.
SLIDE 10 - Transformações em Modelamento
Se escrevemos um ponto medido no sistema i por Pi, podemos escrever esta observação
como
Pw  Pb Tbw
A conversão para coordenadas do “mundo” fica
Pw   PT
b bb Tbw  Pb TbbTbw 
Se o carro vai se mover 10 metros para o norte, a transformação é convenientemente
expressa em coordenadas do “mundo” por uma translação na direção (assumindo que
aponta para o Norte):
Pw  Pb TbwTww 
Neste caso, é multiplicado posteriormente por uma transformação que representa
a mudança. Estes dois exemplos ilustram que a ordem de transformação é
determinada pelo sistema de coordenadas no qual a mudança é mais
convenientemente expressa.
SLIDE 11 - Transformações em Modelamento
Transformações em modelamento são também usadas para instanciar um símbolo em
diferentes localizações em um modelo. Para continuar o exemplo anterior, consideremos os
quatro pneus. Podemos utilizar um único modelo da geometria do pneu e executar quatro
transformações diferentes para especificar onde os pneus deverão estar localizados em
relação ao sistema de coordenadas do “corpo”. O pneu dianteiro direito, por exemplo, é
descrito pela transformação que converte coordenadas medidas no sistema do “pneu” para
o sistema de coordenadas do “corpo”:
Pb  PT
t tb
Se o pneu é rodado em torno do seu eixo , como deve ocorrer quando o automóvel se move
para frente, a transformação para as coordenadas do carro fica
Pb   PT
t tt Ttb  Pt  Ttt Ttb 
onde é uma matriz de rotação primitiva que roda em torno do eixo x. O que é
realmente necessário, obviamente, é converter as coordenadas do pneu para o
sistema de coordenadas do “mundo”. Concatenando todas as transformações
relevantes, obtemos
Pw  Pt  Ttt Ttb Tbw 
SLIDE 12 - Transformações em Visualização
Figura 3 - O sistema de coordenadas do observador tem sua origem no ponto de vista e o
eixo aponta na direção da visão. O sistema de coordenadas é da “mão-esquerda”
Uma transformação V, a transformação de visualização, é usada para converter pontos no
sistema de coordenadas do “mundo” em pontos no sistema de coordenadas do observador
x
e
ye
 
ze 1  xw
yw

zw 1 V
(11)
SLIDE 13 - Transformações em Visualização
Esta transformação pode ser construída a partir de várias translações e rotações que são
determinadas a partir de parâmetros de visualização. A seção 7 tem um exemplo de
derivação de V a partir de parâmetros de visualização.
Figura 4 - A projeção de perspectiva do ponto P na Tela de visualização.
Nós adotamos a convenção que o sistema de coordenadas do “olho” é um sistema de coordenadas
cartesiano de “mão-esquerda”: o eixo aponta para a frente a partir do Ponto de Vista, o eixo para a
direita, e o eixo para cima. Estas convenções são escolhidas de tal forma que os eixos e fiquem
alinhados com os eixos x e y da tela (veja Figura 4). O nome “mão-esquerda” vem do método utilizado
para lembrarmos as relações de eixos. Se colocarmos a mão esquerda em uma posição tal que o polegar
e o indicador estejam estendidos, de tal forma que os mesmos fiquem alinhados com as direções x e y,
respectivamente, a direção z é apontada a partir da palma da mão e pode ser indicada pelo dedo médio.