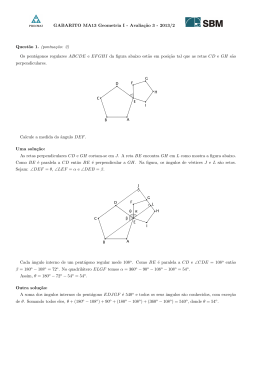
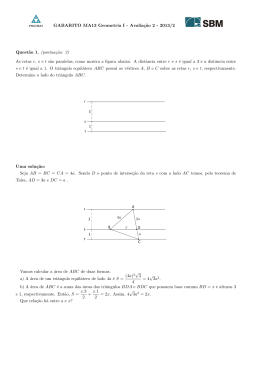
R
Questão .- Use o Teorema de Stokes para calcular C F · dr, onde F(x, y, z) = (x + y 2 )i +
(y + z 2 )j + (z + x2 )k, onde C é o triângulo com vértices (1, 0, 0), (0, 1, 0) e (0, 0, 1), e C é
orientado no sentido anti-horário quando visto de cima.
Solução
Como a curva C é o triângulo com vértices (1, 0, 0), (0, 1, 0) e (0, 0, 1), é claro que C
é uma curva simples, fechada e lisa por partes e a superfı́cie S é formada pela fronteira
de C. De forma que podemos considerar S como sendo a porção do plano que contem os
pontos (1, 0, 0), (0, 1, 0) e (0, 0, 1).
De modo que em primeiro lugar vamos achar a equação do plano P que contem os pontos
(1, 0, 0), (0, 1, 0) e (0, 0, 1). Podemos considerar que P é gerado pelos vetores (−1, 1, 0) =
(0, 1, 0) − (1, 0, 0) e por (−1, 0, 1) = (0, 0, 1) − (1, 0, 0); isto significa que um vetor normal
a P é dado por
i j k
n = −1 1 0 = i + j + k.
−1 0 1 Assim P é da forma x + y + z = d, onde o ponto (0, 0, 1) pertence a P, então 0 + 0 + 1 = d.
Segue-se que a equação do plano P é x + y + z = 1.
Por outro lado, o Teorema de Stokes afirma que
Z
ZZ
F · dr =
rot F · dS.
C
S
i
j
k
∂
∂
∂
rot F = ∂x
∂y
∂z = −2zi − 2xj − 2yk.
x + y 2 y + z 2 z + x2 Então, no caso da superfı́cie S ser dada pelo gráfico z = g(x, y) e dado o campo vertorial
F(x, y, z) = P (x, y, z)i + Q(x, y, z)j + R(x, y, z)k, teriamos que
Z
ZZ
ZZ ∂g
∂g
F · dr =
rot F · dS =
−P
−Q
+ R dA;
∂x
∂y
C
S
D
no nosso caso z = g(x, y) = 1 − x − y; P = −2z; Q = −2x e R = −2y. Então
Z
ZZ
F · dr =
C
(−(−2z)(−1) − (−2x)(−1) + (−2y)) dA;
Z ZD
(−2z − 2x − 2y) dA;
=
Z ZD
Z
F · dr =
ZC
(−2(1 − x − y) − 2x − 2y) dA;
Z ZD
F · dr =
(−2) dA
C
D
onde D é a projeção de S sobre o plano XY , isto significa que
n
.
o
D = (x, y) 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 − x . Logo
Z
Z
1
Z
F · dr =
C
Z
(−2) dydx = −2
0
finalmente,
Z
F · dr = −1.
C
1−x
0
1
(1 − x)dx;
0