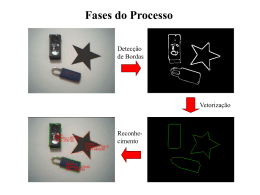
Detecção de Bordas e Linhas I
Paulo Sérgio Rodrigues
PEL205
Conceito de Borda
Conceito de Borda
Conceito de Borda
Técnicas de Detecção de Bordas
(Mapa de Bordas)
Detectores de Mapas de Bordas
basedados em Gradientes
m agf   Gx2  Gy2
1
2
 Gy
 ( x, y )  tan 
 Gx
1
 f 
Gx   x 
f      
Gy   f 
 x 
mag f   G x2  G y2



Detectores de Mapas de Bordas
basedados em Gradientes
Gx (i, j ) 
Zi-1,j-1
Zi-1,j
Zi-1,j+1
Zi,j-1
Zi,j
Zi,j+1
Zi+1,j-1
Zi+1,j
Zi+1,j+1
zi , j 1  zi , j 1
G y (i, j ) 
2
mag f   G  G
2
x
2
y
zi 1, j  zi 1, j
2
 Gy
 ( x, y )  tan 
 Gx
1



Detectores de Mapas de Bordas
basedados em Gradientes
Detectores de Mapas de Bordas
basedados em Gradientes
Detectores de Mapas de Bordas
basedados em Laplaciano
Detectores de Bordas e Linhas
Detectores Baseados em derivadas
Diferença entre Bordas e
Shape (contorno)
Detectar Borda NÃO é Detectar Contorno
Borda, em PDI, NÃO é Contorno
Original
Mapa de Bordas
Contorno
Lidando com Descontinuidade de Bordas
As abordagens vistas até aqui para detecção de bordas e linhas
quase sempre não são eficientes para detectar Contornos em uma
cena. Isso é devido à presença de ruído, descontinuidade de bordas
e relativo baixo contraste entre elas.
O objetivo desta parte da disciplina é definir, dada a saída de um
detector de bordas ou linhas, quais pixels realmente pertencem a
um borda.
Lidando com Descontinuidade de Bordas
Processamento Local
Uma das maneiras mais simples de se definir bordas reais a partir
da saída de um detector é através da análise de características locais.
Os pixels na vizinhança de uma borda possuem características
semelhantes que podem ser usadas para sua detecção. Dada a saída
de um detector como Gradiente, Sobel ou Roberts, pode-se definir
uma borda com base em dois tipos de informação: a) a intensidade
da detecção e b) a direção da detecção.
Lidando com Descontinuidade de Bordas
Processamento Local
Considerando o primeiro critério, pode-se estabelecer um limiar T,
a partir do qual considera-se que um pixel (x’,y’) pertence ou não
a uma borda. Formalmente, a coordenada (x’,y’) de um pixel na
vizinhança de (x,y) é similar em magnitude ao pixel (x,y) se:
f ( x, y)  f ( x' , y' )  T
Lidando com Descontinuidade de Bordas
Processamento Local
Considerando o segundo critério, pode-se também estabelecer um
limiar A (A é um ângulo), a partir do qual considera-se que um
pixel (x’,y’) pertence ou não a uma borda. Se o gradiente de um
pixel qualquer é dado pela equação:
Gy 
1 
 ( x, y )  tan  
 Gx 
então, um pixel (x’,y’) é semelhante a um pixel de uma vizinhança
(x,y) se:
 ( x, y)   ( x' , y' )  A
Lidando com Descontinuidade de Bordas
Processamento Local
Assim, pixels são ligados como pertencentes a mesma região (borda)
se atenderem a ambos aos critérios a) e b).
Região
pixels com mesmas características
Região
pixels com mesmas características
Lidando com Descontinuidade de Bordas
Processamento Local
Lidando com Descontinuidade de Bordas
Processamento Global: Transformada de Hough
Lidando com Descontinuidade de Bordas
Processamento Global: Transformada de Hough
Lidando com Descontinuidade de Bordas
Processamento Global: Transformada de Hough
Lidando com Descontinuidade de Bordas
Processamento Global: Transformada de Hough
Lidando com Descontinuidade de Bordas
Processamento Global: Transformada de Hough
Aplicação da Transformada de Hough
Aplicação da Transformada de Hough
Aplicação da Transformada de Hough
Aplicação da Transformada de Hough
Metodologia
Detecção de Bordas
Detecção de Linhas
Metodologia
Detecção de Linhas
Definição das Regiões de Interesse (ROI)
Metodologia
Definição da ROI
Matching
Aplicação da Transformada de Hough