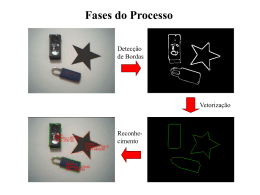
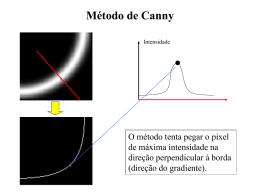
Seminário
Introdução à Visão
Computacional
- The Cyclops Project CPGCC - INE -UFSC
Domínio do Espaço - Parte I
2. Domínio
do Espaço
Parte I - Operações utilizando Convolução
E3. Detecção de Bordas com Convolução Simples
• E3.1 Roberts
• E3.2 Sobel
• E3.3 Robinson
E3’ Operadores Avançados de Detecção de Bordas
• E 3.4 Canny
E3’’ Detecção de Estruturas Salientes
• E 3.5 Sha’aShua
E3. Operações de Detecção de
Bordas
O que é borda ?
É o contorno entre um objeto e o fundo indicando o limite entre
objetos sobrepostos
Variações de intensidade complexas que ocorrem em uma região são
geralmente chamadas de textura. Bordas são definidas como picos da
magnitude do gradiente, ou seja, são variações abruptas da textura
que ocorrem ao longo de curvas dadas pelos valores do gradiente da
imagem.
As bordas são regiões da imagem onde ocorre uma mudança de
intensidade em um certo intervalo do espaço, em uma certa direção.
Isto corresponde a regiões de alta derivada espacial.
E3. Operações de Detecção de
Bordas
E3. Operações de Detecção de
Bordas
O borda unidimensional
E3. Operações de Detecção de
Bordas
O borda bidimensional
E3. Operações de Detecção de
Bordas
Como realizamos a detecção ?
Como uma borda é definida por uma mudança no nível de
cinza, quando ocorre uma denscontinuidade na intensidade, ou
quando o grandiente da imagem tem uma variação abrupta, um
operador que é sensível a estas mudanças operará como um
detector de bordas.
Um operador de derivada faz exatamente esta função. Uma
interpretação de uma derivada seria a taxa de mudança de uma
função, e a taxa de mudança dos níveis de cinza em uma
imagem é maior perto das bordas e menor em áreas
constantes.
E3. Operações de Detecção de
Bordas
Como realizamos a detecção ?
Se pegarmos os valores da intensidade da imagem e acharmos os pontos onde
a derivada é um ponto de máximo, nós teremos marcado suas bordas.
Dado que as imagens são em duas dimensões, é importante considerar
mudanças nos níveis de cinza em muitas direções. Por esta razão, derivadas
parciais das imagens são usadas, com as respectivas direções X e Y. Uma
estimativa da direção atual da borda pode ser obtida usando as derivadas x e
y como os componentes da direção ao longo dos eixos, e computar o vetor
soma.
O operador envolvido é o gradiente, e se a imagem é vista como uma função
de duas variáveis A(x,y) então o gradiente é definido como:
E3. Operações de Detecção de
Bordas
Como implementamos a detecção ?
Um detector de bordas gera:
• uma imagem de gradientes expresso em tons de
cinza (sempre!)
• uma imagem de bordas (onde os pixel com
gradientes irrelevantes foram eliminados)
• uma matriz de vetores de orientação do gradiente
(onde na posição de cada pixel está um valor
indicando a direção principal do gradiente naquele
ponto)
E3.1. Operador de Roberts
É o mais antigo e simples algoritmos de detecção de
bordas. Utiliza um par de matrizes 2x2 para encontrar os
gradientes nas direções x e y:
E3.1. Operador de Roberts
Para determinar onde o pixel avaliado é ou não um pixel de
borda, o gradiente é calculado da seguinte forma:
Se a magnitude calculada é maior do que um valor limite
(parâmetro), o pixel é considerado ser parte de um borda.
E3.1. Operador de Roberts
A direção do gradiente da borda, perpendicular à
direção da borda, é encontrada com a seguinte
fórmula:
E3.1. Operador de Roberts
Problemas:
• O pequeno tamanho da máscara para o operador de
Roberts torna o mesmo fácil de se implementar e rápido
para calcular a máscara de resposta. As respostas,
porém, são muito sensíveis ao ruído na imagem.
• Como a máscara é de tamanho par, a imagem resultante
terá uma linha e uma coluna a menos que a imagem
original
• de fato, o operador calcula o gradiente na posição de um pixel
virtual entre as suas linhas e colunas...
• encher resultante com uma linha e uma coluna pretas...
E3.2. Operador de Sobel
Utiliza duas máscaras para encontrar os
gradientes vertical e horizontal das bordas.
E3.2. Operador de Sobel
• A fórmula para encontrar o gradiente e o ângulo são muito
similares ao operador de Roberts.
• A computação de |G| se torna mais complexa. Na prática |G| é
aproximada da seguinte forma: |G|= |Gx| + |Gy|.
• O módulo do gradiente é proporcional a derivada local da
intensidade.
• O ângulo do gradiente corresponde direção de máxima
variação da intensidade
• Devido as máscaras serem 3X3 ao invés de 2X2, Sobel é muito
menos sensível ao ruído do que Roberts e os resultados são
mais precisos.
E3.3. Operador de Robinson
É similar em operação ao de Sobel, porém usa um conjunto de oito
máscaras, onde quatro delas são as seguintes:
As outras quatro são simplesmente negações destas quatro.
E3.3. Operador de Robinson
• A magnitude do gradiente é o valor máximo obtido ao
aplicar-se cada uma das as oito máscaras ao pixel.
• O ângulo do gradiente pode ser aproximado como o ângulo
na linha de zeros na máscara fornecendo a resposta
máxima.
• Este algoritmo aumenta a precisão de |G|, mas requer
mais computação do que Roberts e Sobel,devido ao
número de máscaras que deve ser aplicado.
• Por outro lado, a determinação do ângulo é simplificada
porque escolhe-se um dentre 8 valores possíveis ao invés
de calculá-lo.
E3.4. Operador de Canny
Proposto por J. Canny em: A computational approach to edge
detection, IEEE Transactions on pattern analysis and machine
intelligence, 8(6), pp 679 – 698 (1986)
Definiu um conjunto de requisitos que um detector de bordas
deveria atender:
1.Taxa de erro: o detector de bordas deve detectar e achar
somente bordas, nenhuma borda deve faltar;
2.Localização: a distância entre os pixels de borda encontradas
pelo detector de bordas e a borda real deve ser a menor possível;
3.Resposta: o detector de bordas não deve identificar múltiplos
pixels de borda onde somente existir um único pixel.
E3.4. Operador de Canny
E3.4. Operador de Canny
O detector de bordas de Canny é um filtro de convolução f que
uniformiza o ruído e localiza as bordas. O problema é identificar
um filtro que otimize os três critérios do detector de bordas:
• Se considerarmos uma borda de uma dimensão variando
no contraste e então convolucionando a borda com a
função de uniformização de Gauss, o resultado será uma
variação contínua do valor inicial ao final, com uma
inclinação máxima no ponto onde existe um "degrau".
• Se esta continuidade é diferenciada em relação a x, esta
inclinação máxima será o máximo da nova função em
relação a original.
E3.4. Operador de Canny
E3.4. Operador de Canny
Os máximos da convolução da máscara e da imagem indicarão bordas
na imagem. Este processo pode ser realizado através do uso de uma
função de Gauss de 2-Dimensões na direção de x e y. Os valores e o
tamanho das máscaras de Gauss dependem da escolha do sigma
(variância) na eq:
E3.4. Operador de Canny
• A aproximação do filtro de Canny para detecção de bordas é G'.
• Convolucionando a imagem com G' obtemos uma imagem I que
mostrará as bordas, mesmo na presença de ruído.
• A convolução é relativamente simples de ser implementada, mas é
cara computacionalmente, especialmente se for em 2D.
• Uma convolução de Gauss de 2D pode ser separada em duas
convoluções de Gauss de 1D.
• O custo computacional do detector de bordas de Canny é
relativamente alto e os resultados são geralmente pósprocessados para maior clareza.
• Entretanto, o algoritmo é mais eficiente no processamento de
imagens com ruídos ou com bordas difusas.
E3.4. Algoritmo do Operador de
Canny
1.Ler a imagem I a ser processada;
2.Criar uma máscara de Gauss de 1D G para convolucionar I. A variância s
de Gauss é um parâmetro fornecido ao detector de bordas;
3.Criar uma máscara de 1-D para a primeira derivada de Gauss nas direções
x e y; nomear como Gx e Gy. O mesmo valor s é usado;
4.Convolucionar a imagem I com G percorrendo as linhas na direção x (Ix)
e percorrer as colunas na direção y (Iy);
5.Convolucionar Ix, com Gx, para dar I´x, o componente x e de I
convolucionado com a derivada de Gauss, e convolucionar Iy, com Gy para
dar I´y;
6.O resultado num ponto é a combinação dos componentes I´x e I´y. A
magnitude do resultado é computada para cada pixel (x,y).
E 3.5 Estruturas Salientes Sha´aShua
•
Introdução
•
Estruturas Salientes
•
A Rede de Saliência
•
O Cálculo da Saliência
•
Exemplos
•
Alguns Problemas
•
Conclusão
E 3.5 Estruturas Salientes Sha´aShua
•
Percepção humana detecta estruturas e formatos
salientes naturalmente
•
Shashua e Ullman propõem um método para se obter
esta percepção
•
Rede de Saliência
•
Avalia a saliência de curvas
•
Baseia-se no comprimento e variação de curvatura
•
Corrige espaços em branco e tremidos nas linhas
•
Gera um Mapa de Saliência
•
Representa os locais salientes da imagem
E 3.5 Estruturas Salientes Sha´aShua
•
Saliência Local
•
Elemento se destaca através de suas propriedades
locais
•
•
•
•
Orientação
Cor
Contraste
Saliência Global
•
Um conjunto de elementos locais torna uma
estrutura globalmente saliente quando se pode
relacioná-los de alguma forma
E 3.5 Estruturas Salientes Sha´aShua
E 3.5 Estruturas Salientes Sha´aShua
E 3.5 Estruturas Salientes Sha´aShua
E 3.5 Estruturas Salientes - Sha´aShua
Requisitos da Rede de Saliência
•
O tempo de detecção de estruturas salientes
não pode depender da complexidade das
curvas de fundo
•
As curvas salientes podem conter falhas e
inconsistências
•
O número de computações deve ser pequeno
E 3.5 Estruturas Salientes - Sha´aShua
Requisitos da Rede de Saliência
•
Locais destacados no mapa de saliência não
precisam ser curvas explícitas na imagem
inicial
•
A medida de saliência não deve ser modificada
após alterações de tamanho, posição e
orientação
E 3.5 Estruturas Salientes - Sha´aShua
A Rede de Saliência
•
Processo computacional
•
•
•
Possui tamanho proporcional ao tamanho da imagem
Realiza iterações locais entre os pontos
•
•
•
•
•
•
Trata os pixels de uma imagem como pontos conectados de
uma rede
Reduz ruídos
Completa espaços em branco
Agrupa segmentos de curvas
Suaviza curvas
Mede a saliência das curvas
Gera um mapa de saliência
•
Exibe a curva mais saliente
E 3.5 Estruturas Salientes - Sha´aShua
O Cálculo da Saliência
•
•
Shashua e Ullman definiram uma função para
calcular a saliência dos fragmentos de uma
curva - Gera Rede de Saliência
•
Cresce de acordo com o comprimento da curva
•
Decresce com a variação da curvatura e com a
quantidade de fragmentos
A medida final é a soma das contribuições das
medidas de saliência dos segmentos
E 3.5 Estruturas Salientes - Sha´aShua
O Cálculo da Saliência
E 3.5 Estruturas Salientes - Sha´aShua
O Cálculo da Saliência
•
Para cada pixel existe um conjunto fixo de
elementos de orientação que conecta o pixel
aos seus vizinhos.
•
Virtual
•
•
Corresponde a uma área vazia na imagem
Real
•
Corresponde a uma área preenchida
E 3.5 Estruturas Salientes - Sha´aShua
O Cálculo da Saliência
E 3.5 Estruturas Salientes - Sha´aShua
O Cálculo da Saliência
E 3.5 Estruturas Salientes - Sha´aShua
O Cálculo da Saliência
E 3.5 Estruturas Salientes - Sha´aShua
O Cálculo da Saliência
E 3.5 Estruturas Salientes - Sha´aShua
O Cálculo da Saliência
Convolução de Gauss
Threshold
Mapa de Saliência
Curva mais Saliente