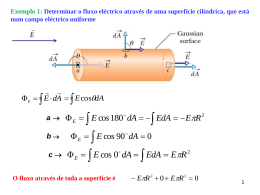
LICENCIATURA EM ENSINO DE FÍSICA – EAD
ELECTRICIDADE: Potencial Eléctrico
Aula – 5
Docente: Moisés João Chambule
1
POTENCIAL ELÉCTRICO
Trabalho e energia potencial eléctrica.
Diferença de potencial.
Gradiente do potencial.
Cálculo de campos através do potencial.
Equações de poisson e Laplace.
1.1.8.1. Trabalho das forças eléctricas
Quando a carga de prova qo se desloca no interior de um
campo eléctrico do ponto A para o ponto B, actuam sobre
ela forças eléctricas que realizam um determinado
trabalho.
Seja ds o deslocamento elementar da carga de prova numa
trajectória rectilínea. Assim considerando Fel uma força
constante em módulo e em direcção.
Definimos trabalho como sendo:
Porque F e S formam um ângulo θ então
3
Se a carga for deslocada do ponto A que dista r1 de Q para o
ponto B que dista r2 de Q, o trabalho realizado será dado
pela integral
Potencial eléctrico
Determinar o trabalho realizado pelo campo eléctrico ao
deslocar a carga de prova no seu seio de r1 à r2.
4
A grandeza
seja
representa diferença de potencial ou
Seja  2 = 0 então W  qo donde   W … potencial
qo
eléctrico.
Def: Potencial elétrico é a capacidade que um corpo
electrizado tem de realizar trabalho, ou seja, a capacidade
de atrair ou repelir outras cargas eléctricas ou ainda
potencial eléctrico é a energia potencial por unidade de
carga.
Unidade: 1J/C= 1V (Volt)
Conclusão: O trabalho a realizar para deslocar uma carga de prova do
infinito para um ponto qualquer no seio do campo eléctrico é igual
ao produto do potencial eléctrico pela carga de prova qo.
5
Quando a carga de prova é deslocada do infinito até um
dado ponto P qualquer no seio do campo eléctrico, o
trabalho das forças eléctricas será negativo e os limites
serão  e P.


W
Sendo  
e Fel  qo E então
qo

 
•Ou     E  ds … potencial eléctrico em termos de campo
eléctrico.
p
Quando as forças eléctricas são conservativas. O trabalho
realizado no campo eléctrico é independente do caminho
percorrido.
P


W1  W2  q o  E  ds
1
P2
6
Se o caminho percorrido for uma linha fechada o trabalho
realizado pelas forças do campo
  conservativas é igual a zero.
W  q o  E  ds  0
1.1.8.3. Noção de Diferença de Potencial
 
  E  ds   12
P2
 
W  q o  E  ds , donde
P2
Sendo
P1
P1
Então W  qo 1  2 
A expressao que esta dentro de parênteses toma o nome de
diferença de potencial U12  1   2
P
W
Assim W  qo  U12 ou seja U   Eds
2
12
 
  Eds
P2
U 12
qo

P1
…diferença de potencial
P1
7
Potencial eléctrico de uma carga eléctrica pontual
8
P
 
   E  ds   E  ds  cos
P

1
   KQ
r


P
ds  cos
dr
  KQ
 KQ  2
2
r

r
P
P
1 1
  KQ  
 r rP 
Como no infinito o potencial tende para zero,
KQ
1 Q …Potencial eléctrico de uma


r
4 o r carga pontual.
Conclusão: O potencial eléctrico de uma carga pontual num
dado ponto do campo eléctrico é inversamente proporcional
à distância r que vai desse ponto à carga eléctrica.
9
Para várias cargas eléctricas distribuídas discretamente
n

teremos:  t  1   2   3  ...   n 
i 1 i

Qi
t 

4 o i 1 r
1
n
Para uma distribuição contínua de cargas teremos
1
dQ
 t   d 
4 o  r
10
Diferença de potencial num campo eléctrico uniforme
A diferença de potencial gera energia eléctrica porque é
justamente ela que permite a passagem de electroes de
um corpo a outro. Se ambos os corpos tiverem o mesmo
potencial eléctrico, não haverá corrida de electroes entre
eles e consequentemente não haverá corrente eléctrica.
Num campo eléctrico constante, a diferença de potencial
entre os pontos a e b é dada por:
 a b  E x
Onde E é o campo eléctrico e x é a distância entre os pontos
a e b.
Em termos do gradiente do potencial e ao longo dos eixos x, y e z o
campo eléctrico é dado pelas expressões:



Ey  
Ez  
x
y
z
Estas equações mostram que a unidade de campo eléctrico também
pode ser o volt/metro (V/m).
Ex  
Equações de Poisson e Laplace.
Da lei de Gauss na forma diferencial, sabemos que:

.E 
0
(1)
E da relação entre o campo e o potencial eléctrico,


vem:
E 
ou E    (2)
r
• Substituindo 2 em 1 teremos:


..   
ou  2  
Eq. de Poison
0
0
Se   0, teremos 2  0 Eq. de Laplace
Superfícies Equipotenciais
São superfície nas quais o potencial é constante. A energia
potencial de um corpo electrizado é a mesma em todos os
pontos desta superfície. Com isto, não há trabalho realizado
para mover o corpo electrizado em tal superfície. Portanto, a
superfície equipotencial, em qualquer ponto, deve ser
perpendicular ao campo eléctrico neste ponto.
A figura mostra as linhas de força do campo eléctrico e as
superfícies equipotenciais.
O MEU MUITO
OBRIGADO
11/5/2015
14