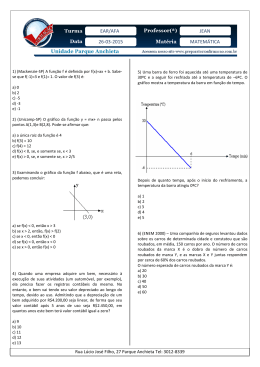
EXERCÍCIOS
CAPÍTULO 3
FUNÇÃO DO 1º GRAU
1) (UFSE) Na figura abaixo tem-se o gráfico da função
do primeiro grau definida por y = ax + b.
1. FUNÇÃO DO 1º GRAU (FUNÇÃO AFIM)
É toda função do tipo f(x) = ax + b, em que a e b são
números reais e a  0 .
Exemplos:
1
f(x) = 2x – 4, f(x) = – 3x + 12, f(x) = 4x e f ( x )  x  1 .
2
Nota: Toda função do 1º grau y = ax + b em que b=0
recebe o nome particular de função linear.
2. GRÁFICO DA FUNÇÃO DO 1º GRAU
O gráfico da função do 1º grau é uma reta oblíqua em
relação aos eixos coordenados, consequentemente,
intercepta ambos os eixos cartesianos.
O valor de a/b é igual a:
a) 3
b) 2
c) 3/2
d) 2/3
e) 1/2
2) (UERJ) A promoção de uma mercadoria em um
supermercado está representada, no gráfico
abaixo, pó 6 pontos de uma mesma reta.
f(x) = x + 2
f(x) = – 2x + 6
y=x
Observações:
1) A função do primeiro grau f(x) = ax + b tem uma
única raiz, que é o valor de x para o qual f(x) = 0;
2) A função do primeiro grau
 é crescente
 x  y quando a  0;
y  ax  b  
é
decrescent
e
 x  y quando a  0.





3) A função f(x) = b não é função
do 1º grau, apesar do seu
gráfico ser uma reta;
Ela é uma função constante.
4) A função linear y = x tem como gráfico uma reta
que passa na origem do sistema cartesiano
formando 45º com o eixo das abscissas e é
chamada Função Identidade.
Exemplos
Ex1. Discutir, em função do parâmetro m, a variação
(decrescente, constante, crescente) da função
y = (m – 1)x + 5;
Resolução: Quando, em uma expressão algébrica,
existe uma variável principal e outras variáveis
secundárias, estas são chamadas parâmetros.
Na expressão y = (m – 1)x + 5, a variável principal é x,
e m é um parâmetro.
O coeficiente de x nessa equação é (m – 1). Assim:
 y é decrescente se m – 1 < 0, ou seja, se m < 1;
 y é constante se m – 1 = 0, ou seja, se m = 1;
 y é crescente se m – 1 > 0, ou seja, se m > 1.
Quem comprar 20 unidades dessa mercadoria, na
promoção, pagará por unidade, em reais, o
equivalente a:
a) 4,50
b) 5,00
c) 5,50
d) 6,00
3) (Unicamp-SP/2005) O custo de uma corrida de táxi
é constituído por um valor inicial Q 0 , fixo, mais um
valor que varia proporcionalmente à distância D
percorrida nessa corrida. Sabe-se que, em uma
corrida na qual foram percorridos 3,6 km, a quantia
cobrada foi de R$ 8,25, e que em outra corrida, de
2,8 km, a quantia cobrada foi de R$ 7,25.
a) Calcule o valor inicial Q 0 .
b) Se, em um dia de trabalho, um taxista arrecadou
R$ 75,00 em 10 corridas, quantos quilômetros seu
carro percorreu naquele dia?
3.
FUNÇÃO DEFINIDA
SENTENÇA
POR
MAIS
DE
UMA
Um elevador é construído segundo as seguintes
especificações:
 para carga de massa menor ou igual a 1.000 Kg,
são usados cabos de aço de 20 mm de diâmetro;
 para carga de massa x Kg, com x > 1.000, são
usados cabos de x/50 mm de diâmetro.
A função seguinte mostra o diâmetro f(x) de cada
cabo, em função da massa x, sendo f(x) em mm e x
em Kg:
 20, se 0  x  1.000

f (x)   x
 50 , se x  1.000

Note que essa função é definida por duas sentenças;
f(x) = 20, se 0  x  1.000
O gráfico de f é:
Perceba, por esse exemplo, que nem sempre é
possível definir uma função através de uma única
sentença y = f(x).
EXERCÍCIO
4) (UFRJ) A cada usuário de energia elétrica é
cobrada uma taxa mensal de acordo com o seu
consumo no período, desde que esse consumo
ultrapasse um determinado nível. Caso contrário, o
consumidor deve pagar uma taxa mínima referente
a custo de manutenção. Em certo mês, o gráfico
consumo (em kWh) x preço (em R$) está
apresentado a seguir:
SÉRIE CASA – FUNÇÃO DO 1º GRAU
1. (Mack-SP 2005) O gráfico esboçado, da função
y  ax  b , representa o custo unitário de produção
de uma peça em função da quantidade mensal
produzida. Para que esse custo unitário seja R$
6,00, a produção mensal deve ser igual a:
a) 930
b) 920
c) 940
d) 960
e) 980
2. (UFPE 2004 adaptada) a poluição atmosférica em
metrópoles aumenta ao longo do dia. Em certo dia,
a concentração de poluentes no ar, às 8h, era de
20 partículas, em cada milhão de partículas, e, às
12h, era de 80 partículas, em cada milhão de
partículas. Admitindo que a variação de poluentes
no ar durante o dia é uma função do 1º grau
(função afim) no tempo, qual o número de
partículas poluentes no ar em cada milhão de
partículas, às 10h20min?
a) 45
b) 50
c) 55
d) 60
e) 65
3. (FGV-SP/2004) Atualmente, o valor de um
computador novo é R$ 3.000,00. Sabendo que seu
valor decresce linearmente com o tempo, de modo
que daqui a 8 anos seu valor será zero, podemos
afirmar que daqui a 3 anos (contados a partir de
hoje) o valor do computador será:
a) R$ 1.875,00
b) R$ 1.800,00
c) R$ 1.825,00
d) R$ 1.850,00
e) R$ 1.900,00
a) Determine entre que valores de consumo em kWh
é cobrada a taxa mínima.
b) Determine o consumo correspondente à taxa de R$
195,00.
4) (UFSM-RS 2005) Sabe-se que o preço a ser pago
por uma corrida de táxi inclui uma parcela fixa, que
é denominada bandeirada, e uma parcela variável,
que é função da distância percorrida. Se o preço da
bandeirada é de R$ 4,60 e o quilômetro rodado é
R$ 0,96, a distância percorrida pelo passageiro que
pagou R$ 19,00, para ir de sua casa ao shopping, é
de
a) 5 Km
b) 10 Km
c) 15 Km
d) 20 Km
e) 25 Km
5) (UFMT 2006) Em uma cidade operam duas
empresas de telefonia fixa. Admita que a empresa
A cobra uma taxa fixa de R$ 30,00 mais R$ 0,15
para cada minuto de ligação local ou interurbana,
que a empresa B cobra uma taxa fixa de R$ 20,00
mais R$ 0,20 para cada minuto de ligação local ou
interurbana. Nessas condições, é mais vantajoso
optar pela empresa A, em planos de, no mínimo,
a) 200 minutos
b) 180 minutos
c) 150 minutos
d) 120 minutos
e) 100 minutos
GABARITOS – CAPÍTULO 3
GABARITO – EXERCÍCIOS – FUNÇÃO 1º GRAU
1) E
2) A
3) a) R$ 3,75. 3b) 30 km.
4) a) [ 0, 50 ]
4b) 180 kWh
GABARITO – SÉRIE CASA – FUNÇÃO 1º GRAU
1) D
2) C
3) A
4) C
5) A