JOSÉ MÁRIO GOMES SILVA “Experiencia realizada com alunos do 12ºAno da Escola Secundária de São Miguel” INSTITUTO SUPERIOR DA EDUCAÇÃO
DEPATAMENTO DE CIÊNCIAS & TECNOLOGIA
2008
JOSÉ MÁRIO GOMES SILVA “Experiencia realizada com alunos da Escola Secundária de São Miguel” TRABALHO CIENTÍFICO APRESENTADO AO ISE PARA OBTENÇÃO DO GRAU DE
LICENCIATURA EM ENSINO DE MATEMÁTICA SOB A ORIENTAÇÃO DE
DR.:ARLINDO TAVARES SEMEDO
2
Dedicatória A todos aqueles que de uma forma ou outra
contribuíram, com o seu apoio, para que este
trabalho se efectivasse.
A todos os meus professores e colegas que me
apoiaram imenso durante a elaboração deste
trabalho
2
O Júri;
__________________________________________________________
__________________________________________________________
__________________________________________________________
Praia, aos ____ de ________________ de 200___
3
Índice I-PARTE ................................................................................................................................................................ 4 INTRODUÇÃO ..................................................................................................................................................... 4 II-PARTE ............................................................................................................................................................... 7 2. PROBLEMA MATEMÁTICO ........................................................................................................................ 7 Fundamentação teórica .................................................................................................... 7 2.1- Problema e exercícios – diferenças............................................................................... 8 2.2- Definição de um problema matemático ....................................................................... 9 2.3 - Formas de expressar problemas matemáticos: ........................................................ 11 2.4 - Classificação de problemas textuais .......................................................................... 12 2.5 - Níveis no desenvolvimento do resolvedor de problemas ......................................... 12 2.5.1- As heurísticas de resolução de problemas .......................................................... 13 2.6 - Etapas da resolução de um problema segundo Polya ............................................. 14 2.7 - Como resolver problemas (segundo Polya). ............................................................. 14 2.7.1- Importância da revisão na resolução de problemas .......................................... 16 III-PARTE ........................................................................................................................................................... 17 3. FUNÇÃO EXPONENCIAL ........................................................................................................................... 17 3.1 - Definição ...................................................................................................................... 17 3.2- Função exponencial y = a x (com a > 0 e a ≠ 1) definidas em (estudo intuitivo) . 18 3.2.1-Função exponencial de base a >1 ......................................................................... 18 3.2.2 - Função exponencial de base a ∈ ]0;1[ ............................................................... 19 3.2.3 - Função exponencial de base e ............................................................................. 20 Limites notáveis ............................................................................................................... 21 3.3 - Translação dos gráficos de funções exponenciais .................................................... 22 3.4-Equações e inequações exponencial ............................................................................ 23 3.4.1-Equações exponenciais .......................................................................................... 23 3.4.2-Inequações exponenciais........................................................................................ 24 3.5-Relação entre função exponencial e função logarítmica ........................................... 25 Logaritmo – definição. .................................................................................................... 25 3.6-Derivada da função exponencial ................................................................................. 26 3.7-Resolução de problemas ............................................................................................... 29 3.7.1-Sugestões metodológicos para a resolução de problemas................................... 29 3.7.2- Problemas propostos............................................................................................. 47 IV-PARTE ........................................................................................................................................................... 49 4-TRABALHO DE CAMPO .............................................................................................................................. 49 4.1-Metodologia ................................................................................................................... 49 4.2-Recolha e tratamento de informações ......................................................................... 52 4.2.1- Organização e reflexão sobre as respostas ......................................................... 52 5-COONCLUSÃO E RECOMENDAÇÔES .................................................................................................... 58 5.1-Conclusão ...................................................................................................................... 58 5.2-Recomendações ............................................................................................................. 60 ANEXO ................................................................................................................................................................ 65 4
I-PARTE
INTRODUÇÃO
Como professor de Matematica durante seis anos, ao longo da carreira tivemos oportunidade
de trabalhar com alunos, cuja a idade vai dos 12 até à idade adulta, contribuindo, deste modo,
na resolução de problemas relacionados com a disciplina de Matemática, e, como é natural,
alguns desses estudantes tinham um talento excepcional para a Matemática, enquanto que
outros a viam como uma disciplina particularmente difícil de aprender. No entanto, a maioria
dos desses alunos manifestaram uma capacidade média em apreender matemática, Durante o
ano lectivo, deu-se uma atenção especial à resolução de problemas, utilizando,
essencialmente, o modelo de resolução função exponencial.
A questão fundamental no ensino de Matemática não é a alteração dos conteúdos, mas sim, a
mudança nos métodos de ensino e na natureza das actividades a realizar com os alunos.
Importa, porém, que o professor faça uma planificação cuidada do processo ensinoaprendizagem, o que implica desafios à actualização científica e pedagógica, à criatividade,
mas também ao equilíbrio e bom senso1.
Sendo assim, deve ser dado um tratamento especial à resolução de problemas utilizando
modelo de resolução função exponencial devido à sua aplicação na vida quotidiana.
1
Ferreira Neves Maria Augusta
Matemática 8 Guia do Professor
5
Os problemas são situações não rotineiras que constituem desafios para os alunos e em que,
frequentemente, podem ser utilizados varias estratégias e métodos de resolução e não
exercícios, geralmente de resolução mecânica e repetitiva, em que apenas se aplica um
algoritmo que conduz directamente à solução.
Como se tem verificado muito insucesso, mais concretamente na disciplina de Matemática e,
dentro da Matemática, a resolução de problemas é um dos factores que contribui para o
insucesso e pelo facto de a resolução de problemas já ter sido objecto de estudo de um
trabalho realizado com alunos do 2º ciclo e, por outro lado, levando em consideração que, no
presente ano lecciono o 12º ano, por esse motivo justifica-se a escolha do tema para o trabalho
do fim do curso: “Resolução de Problemas Matemático Utilizando o Modelo de
Resolução Função Exponencial”, tendo por base a experiência realizada com alunos da
Escola Secundária de São Miguel e cujo objectivo é propor algumas estratégias ou soluções
para diminuir o insucesso ou para melhorar o ensino-aprendizagem da Matemática.
Com o desenvolvimento do tema, pretendo dar um contributo docente, de forma a
proporcionar a organização sistemática dos conhecimentos diacrónicos, e contextualização, de
modo a verificar as diversas contribuições para o desenvolvimento
do processo ensino-aprendizagem e também propor aos professores e alunos algumas
sugestões metodológicas na abordagem da resolução do problema , tendo em conta que a
maioria dos alunos, quando se lhes fala do assunto em destaque começa a “temer”. Com o
mesmo, pretendo, atenuar esse preconceito junto dos referidos alunos, começando por
resolver problemas simples que os cativam para a nova unidade temática.
A par de tudo que ficou exposto acima, esta monografia, pretende, sobretudo:
¾ Identificar as dificuldades dos alunos na resolução de problemas textuais utilizando o
modelo de resolução função exponencial;
¾ Resolver problemas textuais utilizando o modelo de resolução função exponencial;
¾ Aprofundar nos aspectos teóricos e práticos sobre resolução de problemas ;
¾ Identificar as potencialidades na resolução de problemas textuais no desenvolvimento
cognitivos dos alunos;
¾ Desenvolver a competência no sentido de valorizar a resolução de problemas na
organização de processo ensino-aprendizagem da Matemática.
6
O trabalho está estruturado de forma a possibilitar uma leitura abrangente. Na primeira parte
fez-se a introdução, posteriormente realizou-se um pequeno estudo sobre problemas
matemáticos (definição, caracterização, formas de a expressar, classificação, identificação das
etapas e níveis do resolvedor …etc) e, depois, fez-se um estudo da função exponencial para,
de seguida, apresentar o trabalho realizado no campo, bem como o tratamento dos dados
recolhidos. Por último, a conclusão.
7
II-PARTE
2. PROBLEMA MATEMÁTICO
Fundamentação teórica
Viver a Matemática na escola pode ser uma experiência feliz se proporcionarmos aos alunos
experiências matemáticas diversificadas que estejam ao seu alcance e sejam autênticos
desafios aceites com prazer.
A resolução de problemas constitui, em Matemática, um contexto universal de aprendizagem
e deve, por isso, estar sempre presente associada ao raciocínio, à comunicação e integrada
naturalmente nas diversas actividades.
A Matemática é a única ciência onde pouco valor se dá à erudição. O valor de um matemático
é avaliado não pelo que ele sabe mas pela sua capacidade de resolver problemas. E não é para
menos: a Matemática vive de problemas, infelizmente a retórica da Resolução de Problemas
virou um dos modismos do Sistema Escolar nos últimos anos. O resultado é o de se esperar:
os oportunistas de plantão e os ingénuos despreparos conseguiram deturpar de tal modo o
assunto que hoje podemos encontrar as actividades mais ridículas rotuladas como resolução
de problemas matemáticos2.
Um bom problema matemático além de representar um desafio, tanto ao poder dos
matemáticos como ao poder da disciplina por eles criada, também "mexe" com a Matemática:
2
Agnelo, António Mateus, João Matias e Thiago Rodrigo
8
faz com que a melhor entendamos, fertiliza-a e permite que possamos resolver outros
problemas.
2.1- Problema e exercícios – diferenças
“O que para alguns é um problema para outros é um exercício e para alguns outros uma
distracção”. (Ditado popular).
Muitas vezes o professor de Matemática costuma pedir ao aluno para resolver exercícios ou
problemas, e até os livros didácticos induzem a utilizar esta palavra - para aprender um
determinado tópico da matéria. Ou seja, é preciso diferenciar problema de exercício, palavras
estas, muitas vezes utilizadas como equivalentes pelos professores de Matemática.
O exercício é uma actividade de adestramento no uso de alguma habilidade ou conhecimento
matemático já conhecido pelo resolvedor, como a aplicação de algum algoritmo ou fórmula já
conhecida. Ou seja, o exercício envolve mera aplicação de resultados teóricos enquanto o
problema necessariamente envolve invenção e/ou criação significativa, mais concretamente
Um problema é uma tarefa na qual o individuo ou grupo se confronta com a necessidade de
encontrar uma solução, não possuindo um procedimento directamente acessível que garanta a
solução.
Um matemático, ao descrever o seu trabalho, certamente não deixará de pronunciar duas
palavras presentes no seu dia a dia: problema e prova.
O problema é o meio pelo qual a Matemática se desenvolve, ou seja, o “alimento” da
evolução matemática. Um problema tem seu grau de importância relacionado à quantidade de
ideias novas que ele traz à Matemática e o quão ele é capaz de impulsionar os diversos ramos
da Matemática – sobretudo aqueles em que ele não está directamente relacionado.
A prova está indissoluvelmente ligada ao problema e é a única maneira de atestar ou não a
solução Matemática do mesmo. A prova representa o rigor, a solidez e a consistência da teoria
Matemática e nada mais é do que uma sequência de raciocínios dedutivos que parte de fatos
de veracidade já conhecida – como teoremas e axiomas – e chega até o resultado em
demonstração, resolvendo o problema.
9
No contexto de educação Matemática, um problema, ainda que simples, pode suscitar o gosto
pelo trabalho mental se desafiar à curiosidade e proporcionar ao aluno o gosto pela descoberta
da resolução. Neste sentido, os problemas podem estimular a curiosidade do aluno e fazê-lo a
se interessar pela Matemática, de modo que ao tentar resolvê-los o aluno adquire criatividade
e aprimora o raciocínio além de utilizar e ampliar o seu conhecimento matemático.
2.2- O que é um problema?
Agora que falamos da importância dos problemas na Matemática, podemos dar uma definição
intuitiva de problema.
Existem diversas concepções acerca do que é um problema:
Para Newell & Simon (1972), “um problema é uma situação na qual um indivíduo deseja
fazer algo, porém desconhece o caminho das acções necessárias para concretizar a sua acção”
Segundo Chi e Glaser (1983) “o problema é uma situação na qual um indivíduo actua com o
propósito de alcançar uma meta utilizando para tal alguma estratégia em particular”
Definição- (segundo Polya )
Um problema matemático é toda situação requerendo a descoberta de informações
matemáticas desconhecidas para a pessoa que tenta resolve-lo, e/ou a invenção de uma
demonstração de um resultado matemático dado. O fundamental é que o resolvedor tenha de
inventar estratégias e criar ideias; ou seja: pode até ocorrer que o resolvedor conheça o
objectivo a chegar, mas só estará enfrentando um problema se ele ainda não tem os meios
para atingir tal.
O quadro teórico sobre a resolução de problemas considerado adequado e por isso adoptado,
foi o Modelo de Resolução de Problemas de Polya. Tal modelo, foi apresentado aos alunos
numa aula, através de uma transparência, comportando as diversas fases (mais simplificadas),
acompanhadas de um exemplo prático e de muito simples de aplicação.
10
De acordo com a definição dada pelos autores podemos concluir que a palavra “problema”
tem conotações diferentes de indivíduo para indivíduo e por isso, torna necessário caracterizar
o sentido que lhe damos.
Perfilhamos a ideia que Kantowski (1977) traduz na seguinte afirmação:“Um indivíduo está
perante um problema quando se confronta com uma questão a que não pode dar resposta ou
com uma situação que não sabe resolver, usando conhecimentos imediatamente disponíveis”
Podemos destacar alguns exemplos que ilustram a situação acima referida:
1-No torneio de ténis de mesa, que se vai. Realizar numa escola, estão inscrito 92
participantes. Cada participante necessita de 3 bolas. Quantas bolas serão distribuídas?
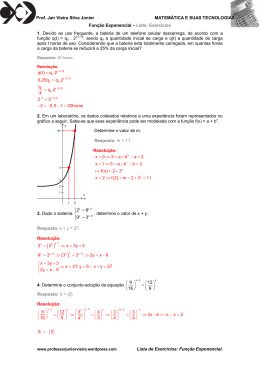
2- A função f (t ) = 1000e1,2t traduz o crescimento de uma certa população de insectos
(t representa o tempo em semanas).
Mostra que a variação da função é proporcional à própria função. Qual é o significado desta
relação?
A premeria questão para alunos do 4º ano do E.B.I é um problema, não será um problema
para um aluno do3ºciclo ensino secundário, pois no seu repertório de conhecimento faz parte
o algoritmo da multiplicação. Trata-se de um simples exercício de aplicação. No entanto, para
os mesmos alunos, a segunda questão já constitui um problema. Será necessário descobrir um
caminho que lhes permita dar a resposta.
2.2- Características de um problema proposto a um resolvedor
A partir das concepções de problemas acima, entendemos que existe um problema quando há
um objectivo a ser alcançado e não sabemos como atingir esse objectivo. Em Matemática,
existe um problema quando há um resultado – conhecido ou não – a ser alcançado utilizando
a teoria Matemática.
Um problema é mais valioso à medida que o resolvedor – ou seja, quem está se propondo a
encontrar uma solução ao problema - tenha de inventar estratégias e criar ideias. Quem
resolve pode até saber o objectivo a ser atingido, mas ainda estará enfrentando um problema
se ele ainda não dispõe dos meios para atingir tal objectivo.
11
Dai há necessidade de identificar algumas características de um problema proposto ao
resolvedor:
Segundo Resnick
Ö
Um problema tem várias características
•
sem algoritmização - o caminho da resolução é desconhecido, ao menos em
boa parte;
•
complexos - precisam de vários pontos de vista;
•
exigente -a solução só é atingida após intenso trabalho mental; embora o
caminho possa ser curto, ele tende a ser difícil;
•
exigem lucidez e paciência para na aparente desordem vermos as
regularidades, os padrões que permitirão a construção do caminho até a
solução;
•
nebulosos- podem ocorrer que nem todas as informações necessárias estejam
aparentes; por outro lado, pode ocorrer que existam conflitos entre as
condições estabelecidas pelo problema;
•
não há resposta única além de normalmente ocorrer de existirem várias
maneiras de se resolver um dado problema, pode ocorrer de não existir uma
melhor solução e até de não existir solução; ao contrário do que a Escola
ensina:
2.3 - Formas de expressar problemas Matemáticos:
•
Texto e esquema;
•
Texto e gráfico;
•
Texto e tabela;
•
Texto e figura;
•
Texto e equação / inequação;
•
Texto.
12
2.4 - Classificação de problemas textuais
Tendo em conta que o trabalho a ser realizado é sobre problemas textuais utilizando modelo
de resolução função exponencial há necessidade de avaliar os problemas textuais.
Os problemas textuais podem ser classificados segundo os seguintes critérios:
Ö
Conteúdo do problema (ex: problemas sobre: movimento, trabalho conjunto,
moedas, números, idades, misturas de líquidos, figuras geométricas,...);
Ö
Nível de abstracção (ex: problemas práticos e teóricos);
Ö
Método de resolução (ex: problemas: algébricos, lógicos, geométricos; problemas
que se resolvem utilizando “instrumentos” de análise Matemática).
2.5 - Níveis no desenvolvimento do resolvedor de problemas
Na resolução de problemas existem indivíduos com diferentes características, a ideia
defendida pelo matemático Kantowski que os classificou de acordo com as capacidades
pessoais de resolver problemas matemáticos em seguintes estágios:
•
Inerte:
a pessoa tem nenhum ou quase nenhum entendimento do que seja resolver um
problema matemático; em particular, não é capaz de atinar por onde começar. O
máximo que se consegue fazer nesse estágio é reproduzir procedimentos de
resolução muito simples e que foram exaustivamente explicados e exemplificados.
Ou seja: uma pessoa nesse estágio está restrita ao mundo dos exercícios, e é
necessário que esses sejam bastante exemplificados;
•
Imitador:
com pouca explicação e exemplificação, torna-se capaz de fazer exercícios mas
ainda não é capaz de resolver verdadeiros problemas; é capaz de participar
produtivamente em grupos que estejam discutindo a resolução de problemas de
tipo novo, contudo é incapaz de trabalhar sozinho;
•
Capaz:
atingiu a capacidade de resolver problemas, mas esses devem ser variantes
relativamente simples de problemas que aprendeu ou já resolveu;
•
Avançado:
além de demonstrar uma capacidade superior de resolução, através da velocidade
13
de resolução, da variedade e da maior complexidade dos problemas que é capaz de
enfrentar, a pessoa começa a ser capaz de conceber processos de resolução
diferentes dos que tinha aprendido;
•
Artista:
a pessoa não só atingiu uma proficiência superior de inventar novos processos de
resolução como preocupa-se em explorar caminhos alternativos, buscando
resoluções mais elegantes ou poderosas.
2.5.1- As heurísticas de resolução de problemas
Antes de entrarmos na exposição e análise das diversas heurísticas de resolução de problemas
é muito importante termos uma ideia clara sobre o significado da palavra heurística. Para tal,
recorremos ao dicionário Houaiss que nos “traduz” heurística em vários contextos:
¾ Contexto científico: “a ciência que tem por objectivo a descoberta dos fatos”3;
¾ Contexto de problematização: “a arte de inventar, de fazer descobertas” ou “método de
investigação baseado na aproximação progressiva de um dado problema”;
¾ Contexto pedagógico: “método educacional que consiste em fazer descobrir pelo
aluno o que se lhe quer ensinar”.
Percebemos, portanto, que falar em heurística de resolução de problemas é falar sobre
“métodos e regras que conduzem à descoberta, inovação, investigação e resolução de
problemas.
Podemos também observar que heurística pode referir-se tanto ao contexto científico quanto
ao contexto educacional; para nós, ambos os contextos são pertinentes, pois ao mesmo tempo
em que queremos avaliar a importância da resolução dos problemas na evolução da
Matemática – descoberta de novos resultados, criação de novos, problemas,..., etc. - também
queremos ressaltar a importância dos problemas no processo ensino-aprendizagem
3
HOUAISS, António et al. Dicionário Houaiss da Língua Portuguesa. Rio de Janeiro, Objetiva, 2001, 1ª ed., p. 1524.
FERREIRA, Aurélio Buarque de Holanda. Novo Aurélio – O dicionário da língua portuguesa. Rio de Janeiro, Nova Fronteira,
2000, 3ª edição
14
2.6 - Etapas da resolução de um problema segundo Polya
Muitas vezes a pessoa que está perante um problema matemático começa a resolver um
problema sem entender o problema mas não é preciso ter preça, um problema antes de ser
resolvido é preciso entender e estabelecer um plano de acção.
Procurando organizar um pouco o processo de resolução de problemas, o grande matemático
George Polya o dividiu em quatro etapas, que resumimos abaixo. Antes de passarmos a elas,
é muito importante enfatizar que Polya nunca pretendeu que sua divisão correspondesse à
uma sequência de etapas a serem percorridas uma após outra, sem que nunca seja conveniente
ou necessário voltar atrás que funcionasse como uma “poção mágica” para resolver problemas
matemáticos.
E dela podemos destacar tais como:
o
1-Entendimento do problema;
o
2-Invenção de estratégias de resolução;
o
3-Resolução/execução;
o
4-Revisão.
2.7 - Como resolver problemas (segundo Polya).
1- Entenda o problema:
•
Primeiro, tens de entender o problema:
•
Qual é a incógnita? Quais são os dados? Quais são as condições?
•
É possível satisfazer as condições? Elas são suficientes para determinar a incógnita?
Ou são insuficientes? Ou redundantes? Ou contraditórias?
•
Faça uma figura. Outra se necessário. Introduza notação adequada.
•
Separe as condições em partes.
2- Construa uma estratégia de resolução
Ache conexões entre os dados e a incógnita. Talvez seja conveniente considerar problemas
auxiliares ou particulares, se uma conexão não for achada em tempo razoável. Use isso para
"bolar" um plano ou estratégia de resolução do problema.
15
Vale a pena expandirmos um pouco esses conselhos:
•
Já encontrou este problema ou algum parecido?
•
Conhece um problema semelhante? Conhece teoremas ou fórmulas que possam
ajudar?
•
Olhe para a incógnita! E tente achar um problema familiar e que tenha uma incógnita
semelhante.
•
Aqui está um problema relacionado com o seu e que você já sabe resolver. Conse--gue
aproveitá-lo? Pode usar seu resultado? Ou seu método? Deve-se introduzir algum
elemento auxiliar de modo a viabilizar esses objectivos?
•
Consegues enunciar o problema de uma outra maneira?
•
Se não conseguiu resolver o problema dado, tente resolver um problema parecido.
Consegue imaginar um caso particular mais acessível? Um caso mais geral e mais
acessível? Consegues resolver alguma parte do problema? Mantenha apenas parte das
condições do problema e observe o que ocorre com a incógnita, como ela varia agora?
Consegues obter alguma coisa desde os dados? Consegues imaginar outros dados
capazes de produzir a incógnita? Consegues alterar a incógnita ou os dados, ou ambos,
de modo que a nova incógnita e os novos dados fiquem mais próximos?
•
Estás a levar em conta todos os dados? E todas as condições?
3- Execute a estratégia
Frequentemente, esta é a etapa mais fácil do processo de resolução de um problema. Contudo,
a maioria dos principiantes tendem a pular para essa etapa prematuramente, e acabam dandose mal. Outros elaboram estratégias inadequadas e acabam se enredando terrivelmente na
execução.
•
Execute a estratégia.
•
Ao executar a estratégia, verifique cada passo que consegues mostrar claramente que
cada um deles está correcto?
4 - Reveja
•
Examine a solução obtida.
•
Verifique o resultado e o argumento.
•
Você pode obter a solução de um outro modo?
16
•
Qual a essência do problema e do método de resolução empregado? Em particular,
você consegue usar o resultado, ou o método, em algum outro problema?
2.7.1- Importância da revisão na resolução de problemas
1- A revisão é a última etapa da resolução, (segundo Polya)
Conforme vimos em texto anterior, Polya dividiu o processo de resolução de problemas
matemáticos em quatro etapas: entendimento do problema, invenção de estratégia de
resolução, execução e revisão.
Poderíamos dizer que Polya pretendia duas coisas nessa última etapa:
•
Uma depuração da resolução
•
Uma abstracção da resolução
Antes de passarmos a detalhes, observemos que na Escola existem ao menos caricaturas das
três primeiras etapas de Polya, mas nada no que toca à etapa da revisão. Os professores ou
ignoram essa importante etapa ou alegam que a mesma é inviável de trabalhar face à falta de
tempo, dificuldade de testar, frustração dos alunos, etc.
2- Reveja para depurar a resolução
O objectivo é verificar a argumentação usada, procurando simplificá-la. Pode-se chegar ao
extremo de buscar outras maneiras de resolver o problema, possivelmente mais simples, mas
menos intuitivas e só agora acessíveis ao resolvedor.
3- Reveja para abstrair a resolução
Agora, o objectivo é reflectir no processo de resolução procurando descobrir a essência do
problema e do método de resolução empregado. Tendo-se sucesso nessa empreitada, poderse-á resolver outros problemas mais gerais ou de aparência bastante diferente. Ela representa a
possibilidade de aumento do "poder de fogo" do resolvedor. Feito por matemático talentoso,
esse trabalho de depuração representa a possibilidade de fertilização da Matemática.
17
III-PARTE
3. FUNÇÃO EXPONENCIAL
3.1 - Definição
Chama-se função exponencial a uma função que tem expressão analítica do tipo a x
(a ∈
•
+
\ {1} e x ∈
.
Para estudar esta função é preciso recordar a noção de potência, sendo assim
enunciamos algumas propriedades:
Seja a, b ∈
e ∀x, y ∈
a) a 0 = 1
1
ax
= ax × a y
b) a − x =
c) a x + y
d ) a x× y = ( a x )
y
e) 1x = 1
x
1
⎛1⎞
f)⎜ ⎟ = x
a
⎝a⎠
h) ( a × b ) = a x × b x
x
Potência
Definiu-se potência de expoente natural n dum número real a, por an ,sendo
a → base
x → expoente
⎧⎪a1 = a
⎨ n
n −1
⎪⎩a = a × a ;
n = 2,3, 4,........
18
3.2- Função exponencial y = a x (com a > 0 e a ≠ 1) definidas em
(estudo intuitivo)
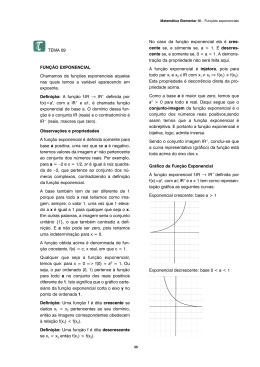
3.2.1-Função exponencial de base a >1
Seja a um número real positivo. A aplicação
f :
→
+
, com f ( x) = a x
Chama-se função exponencial de base a
Vamos estudar algumas propriedades desta função.
(1) O domínio da função é
.
(2) Como a>1 então a x > 0, ∀x ∈
logo o contradomínio da função é
(2) Sendo a > 1, x2 > x1 ⇒ a x2 > a x1 , ∀x1 , x2 ∈
+
.
, então f é crescente.
Cresce mais rapidamente quando maior for o valor de a e para cada a o crescimento é
mais rápido para os valores maiores de x
(3) Seja x1 ≠ x2 ⇒ a x1 ≠ a x2 , ∀x1 , x2 ∈
logo f é injectiva.
(4) A função não tem zeros visto que a x > 0, ∀x ∈
.
(5) Pontos da intercessão com eixo das ordenadas (0,1)
0 ∈ D f ⇒ f (0) = a 0 = 1
(6) lim a x = +∞
x →+∞
e lim a x = lim a − x = lim
x →−∞
x →+∞
x →−∞
1
= 0 (ver a tabela pag.25).
ax
(7) Admite a assimptota horizontal de equação y=0 quando x → −∞ e não tem
assimptotas verticais nem oblíquos.
(8) Esboço do gráfico
19
3.2.2 - Função exponencial de base a ∈ ]0;1[
Seja a um número real positivo. A aplicação
f :
→
+
, com f ( x) = a x
Chama-se função exponencial de base a
Vamos estudar algumas propriedades desta função.
(1) O domínio da função é
.
(2) Como 0 < a < 1 então a x > 0, ∀x ∈
então o contradomínio da função é
(2) Sendo 0 < a < 1, x2 > x1 ⇒ a x2 < a x1 , ∀x1 , x2 ∈
+
.
então f é decrescente.
Decresce mais rapidamente quando maior for o valor de a e para cada a o decrescimento é
mais rápido para os valores maiores de x
(3) Seja x1 ≠ x2 ⇒ a x1 ≠ a x2 , ∀x1 , x2 ∈
logo f é injectiva.
(4) A função não tem zeros visto que a x > 0, ∀x ∈
.
(5) Pontos da intercessão com eixo das ordenadas (0,1)
0 ∈ D f ⇒ f (0) = a 0 = 1
(6)
0 < a <1⇒
1
> 1;
a
x
⎛1⎞
seja g ( x) = a e seja f ( x) = ⎜ ⎟ = a − x
⎝a⎠
x
Então f(x) identifica-se com g(-x), ou seja, g(x)=f(-x) , portanto os gráficos de f e de g são
simétricos em relação ao eixo das ordenadas.
Então o limite lim a x = +∞
x →−∞
e lim a x = 0
x →+∞
(7) Admite a assimptota horizontal de equação y=0 quando x → +∞ e não tem
assimptotas verticais nem oblíquos.
(8) Esboço do gráfico
20
3.2.3 - Função exponencial de base e
Já estudamos várias funções exponenciais de base superior a 1. Tem particular interesse
estudar a função cuja base é o número e 2,71828…. que é designado por número de Neper .
Define-se função exponencial de base e a função:
→
f:
+
x a ex
Esta função goza das mesmas propriedades que qualquer outra função exponencial de base
superior a 1 e aparece na descrição de vários fenómenos.
Observe o gráfico
Característica da função exponencial de base e:
y = ex
Dominio
+
Contradominio
Zeros
não tem
Sinal
Positiva
Monotonia
injectividade
Assimptotas
Crescente
injectiva
horizontal y = 0
comportamento nos etretremos docontradominio
lim e x = 0
x →−∞
lim e x = +∞
x →+∞
21
Limites notáveis
•
ax
= +∞ ∀k ∈
x →+∞ x k
O crescimento de a x , com a> 1, é tão rápido que se tem lim
“a exponencial cresce mais depressa do que qualquer potencia do seu expoente “ como
xk
= 0 , ∀k ∈
x →+∞ a x
consequência, tem-se obviamente lim
visto que o inverso dum infinitamente
grande é um infinitésimo.
Exemplo
2x
=
x →+∞ x 4
lim
Já sabemos que
lim 2 x = +∞
e
x →+∞
indeterminação do tipo
lim x 4 = +∞ , logo estamos perante uma
x →+∞
∞
.
∞
Podemos determinar alguns valores construindo uma tabela.
X
…
1
2
3
…
50
…
100
…
2x
…
2
4
8
…
250
…
2100
…
x4
…
1
16
81
…
504
…
1004
…
2x
x4
…
2
1
4
8
81
… ≈ 1,8 × 108 …
≈ 1,3 × 1022
…
2x
Facilmente podemos ver 4 toma valores tão grandes quanto se queira, maiores que
x
qualquer número dado, quando x aumenta indefinidamente.
•
Experimenta dar a x valores cada vez mais próximos de zero, positivos ou negativos, e
verifica (com a calculadora) que
ex − 1
toma valores cada vez mais próximos de 1. O
x
facto da tangente ao gráfico de e x , no ponto (0,1) , permite ter declive 1 e escrever
ex − 1
=1
x →0
x
lim
22
3.3 - Translação dos gráficos de funções exponenciais
Partindo do conhecimento do gráfico da função : a x , a > 0 e a ≠ 1
Por translação é possível obter o gráfico da função do tipo:
y = b + a( x+d )
Exemplos:
Ver anexo (pag.66)
23
3.4-Equações e inequações exponencial
3.4.1-Equações exponenciais
Equação exponencial tem este nome porque apresenta a incógnita em algum expoente. Numa
equação exponencial encontraremos potências em que a base será conhecida e o valor do
expoente será desconhecido, ou seja, será uma incógnita.
Ex: 52 x +3 = 3125
Resolução de equações exponenciais:
É conveniente saber que nem todas as equações exponenciais podem ser resolvidas.
A existência de poderosos computadores e grandes centros de computação
permitem obter aproximações muito precisas, mas as soluções exactas
geralmente não são possíveis.
Vamos estudar alguns exemplos resolvidos. O que pretendemos é demonstrar como, a partir
de algumas etapas simples, é possível transformar uma equação exponencial numa igualdade
de duas potências da mesma base.
Para lembrar:
É importante observar os passos dados até aqui para resolver os
exemplos seguintes de equações exponenciais.
Exemplo:
a) 3x = 81 ⇔ 3x = 34 ⇔ x = 4
b) 2 x −5 = 16 ⇔ 2 x −5 = 24 ⇔ x − 5 = 4 ⇔ x = 9
c) 52 x +3 = 3125 ⇔ 52 x +3 = 55 ⇔ 2 x + 3 = 5 ⇔ 2 x = 5 − 3 ⇔ x = 1
Analisando os passos ali dados podemos concluir que para resolver essas equações é
necessário realizar dois passos importantes:
1º ) Reduzir os dois membros da equação a potencia de mesma base
2º) Aplicar a propriedade:
a x = a y ⇔ x = y (a ≠ 1 e a > 0)
24
3.4.2-Inequações exponenciais
Inequação exponencial -uma desigualdade em que a incógnita figura em expoente.
2 2 + x > 1 ⇔ 2 2 + x > 2 0 ⇒ 2 + x > 0 ⇔ x > −2
Ex:
CS = ]−2; +∞[
Propriedade que nos permite resolver inequações exponenciais:
+
Se a ∈
, r1 , r2 ∈
en tã o :
1−
a > 1 ∧ r1 > r2 ⇒ a r1 > a r2
2−
a < 1 ∧ r1 > r2 ⇒ a r1 < a r2
Exemplos:
1-Resolve as seguintes inequações:
a) 2 x−2 − 8 > 0
1−
x
⎛1⎞ 2
b) ⎜ ⎟ > 3x
⎝3⎠
c) x × 5x − 4 × 5x ≥ 0
a) 2
x−2
−8 > 0⇔ 2
x
2
x−2
>8⇔ 2
x
2
x−2
Resolução
> 2 ⇒ x − 2 > 3 ⇔ x > 3 + 2 ⇔ x > 5.... CS = ]5; +∞[
3
x
x
1−
−x
⎛ ⎛ 1 ⎞ −1 ⎞
x
2 x −2 x
⎛1⎞ 2 ⎛1⎞
> ⎜⎜ ⎟ ⎟ ⇔ ⎜ ⎟ > ⎜ ⎟ ⇒ 1− < −x ⇔ − <
⇔
⎜⎝ 3 ⎠ ⎟
2
2 2
2
⎝ 3⎠
⎝ 3⎠
⎝
⎠
⇔ 2 − x < −2 x ⇔ − x + 2 x < −2 ⇔ x < −2 ....CS = ]−∞; −2[
1−
⎛1⎞
b) ⎜ ⎟
⎝3⎠
1−
⎛1⎞
>3 ⇔ ⎜ ⎟
⎝3⎠
x
c) x × 5 x − 4 × 5 x ≥ 0 ⇔ 5 x ( x − 4 ) ≥ 0 ⇔ ( como 5x > 0 ) para que 5x ( x − 4 ) ≥ 0 x − 4 ≥ 0 ⇒ x ≥ 4
CS = [ 4; +∞[
Outra forma de resolver
x
−∞
x
+
5
x−4
x
5 ( x − 4)
CS = [ 4; +∞[
4
54
0
0
+∞
+
+
+
25
3.5-Relação entre função exponencial e função logarítmica
Logaritmo – definição.
Dados dois números a e b positivos a ≠ 1 chama-se logaritmo na base a de b
número x tal que a = b ⇔ x = log a b
Exemplos:
a ) log 3 81 = 4 porque 34 = 81
b) log 2 64 = 6
( log a b )
o
x
porque 26 = 64
c) log1000 = 3 porque 103 = 1000 c) ln e3 = 3 porque e3 = e3
A partir do gráfico da função exponencial podemos fazer o esboço do gráfico da função
logarítmica tendo em conta que a função logarítmica é a inversa da função exponencial
Função logarítmica
Vimos no parágrafo anterior que a função x → a x , com a ∈
bijecção que aplicava
sobre
+
+
, a ≠ 1, e´ uma
.
A função inversa desta função exponencial chama-se função logarítmica na base a. Trata-se,
então, da função x → log a x
Assim, podemos obter o gráfico f −1 , desenhando o gráfico de , a recta y = x , e o simétrico
de cada ponto ( x, y ) do gráfico de f relativamente à recta y = x .
26
A partir do gráfico da função
y = ax
esboça o gráfico
+
y = log a x com a, x ∈ e a ≠ 1 compara as características das funções.
da
função
Comparando as duas funções:
y = ax
y = log a x com a > 1
+
Dominio
+
Contradominio
Zeros
não tem
x =1
(log a 1 = 0)
Sinal
Positiva
negativa em ]0,1[
Positiva em ]1,+∞[
Monotonia
Crescente
Crescente
injectividade
injectiva
injectiva
horizontal y = 0
Assimptotas
Limites importantes
lim a = 0
x
x →−∞
lim a x = +∞
x →+∞
vertical x = 0
lim log a x = −∞
x → 0+
lim log a x = +∞
x →+∞
3.6-Derivada da função exponencial
Comecemos por calcular a derivada da função exponencial de base e , g ( x) = e x .
Por definição:
g ( x + h) − g ( x )
e x+h − e x
e x × eh − e x
eh − 1
eh − 1
x
x
g `( x) = lim
= lim
= lim
= lim e ×
= e × lim
=
h →0
h →0
h →0
h→0
h →0
h
h
h
h
h
= ex ×1 = ex
vem (e x )`= e x
Regra:
A derivada da função exponencial de base e é dada por:
(e x )`= e x
Sendo u = f ( x) função, tem-se
(eu )`= u `×eu
Nota: A função exponencial é a única função cuja expressão da derivada coincide com a
própria função.
Exemplo:
(e3 x )`= (3x)`×e3 x = 3e3 x
Derivada da função exponencial de base a> 1
Calculemos agora a derivada de uma função exponencial de base a> 1. Seja g ( x) = a x .
Por definição de logaritmo, sabemos que:
27
a = eln a donde , a x = ( eln a ) = e x ln a
x
Aplicando a definição da derivada da exponencial de base e, vem:
( a ) = ( e ) = ( x ln a ) × e
x `
x ln a `
`
x ln a
= ln a × e x ln a = ln a × a x
Poranto,
(a )
x `
= ln a × a x
Sendo f ( x) uma função, vem:
(a )
f ( x) `
= ln a × f `( x) × a f ( x )
ou
(a )
u `
= ln a × u`× a u com u = f ( x)
Regra:
A derivada de uma função exponencial de base a>1 é dada por:
(a )
x `
= ln a × a x
Sendo u = f ( x) uma função, tem-se: ( a u ) = ln a × u `× a u
`
Exemplos
a ) f `( x) = ( e 4 x ) = ( 4 x ) × e 4 x = 4e 4 x
`
`
`
4x
4x
4x
4x
⎛ 34 x ⎞ ( 3 ) × x − 3 × x` ln 3 × ( 4 x )`×3 × x − 3 × 1 ln 3 × 4 × 34 x × x − 34 x
b) g `( x) = ⎜
=
=
=
⎟ =
x2
x2
x2
⎝ x ⎠
4x
ln 3 × 4 x × 34 x − 34 x 3 ( 4 x ln 3 − 1)
=
=
x2
x2
`
Exercícios propostos
1-Resolve as seguintes condições:
d ) 23 x + 2 = 2
a) 32 × 3-x+1 = 34
b) 16 x − 2 × 22 x − 8 × 2 x + 8 = 0
c) ( 2x ) = 16 × 8x
x
g ) x 2 e x + 3xe x = 0
2
⎛1⎞
e) ⎜ x ⎟ − 3e x + 2 = 0
⎝e ⎠
f ) e x − e2 x = 0
h) 2 x
2
−5 x
=
1
64
i ) e x + 2 − 4 x 2 .e x = 0
j ) 2e x + e− x − 3 = 0
k ) 2 x +3 + 4 x +1 = 320
28
1−
x
2
l )2x−2 − 8 > 0
⎛1⎞
m) ⎜ ⎟
⎝ 3⎠
o) 3x − 27 < 0
p) ( 0.1) < 103
⎛1⎞
r) ⎜ ⎟
⎝ 10 ⎠
> 3x
n) x × 5x − 4 × 5x > 0
k ) x2 × 2x−1 > 0
x
x −4
> 10
s) − xex + 2ex < 0
t ) e x + 2 − 4 x2 e x ≥ 0
2- Calcule a derivada de cada uma das funções seguintes:
a) h(x) = 2x
d ) i( x ) = 2 xe 4 x
b) f (x) = e
ex
e) k (x) =
x
34x
f ) g (x) =
x
4x
c) j( x) = 32x
3
+7x
29
3.7-Resolução de problemas
3.7.1-Sugestões metodológicos para a resolução de problemas
O termo “crescimento exponencial “é muitas vezes utilizado para caracterizar um fenómeno
de crescimento cada vez mais rápido, embora o modelo matemático dessa realidade nem
sempre seja uma progressão geométrica. O desenvolvimento de uma doença, a propagação de
um boato, o crescimento de uma população, é exemplos de situações em que aquele termo é
usado.
um boato
Supõe que no dia 1 de Abril alguém (nos boatos nunca se sabe quem começa) se lembra de
lançar um boato e que, cada dia que passa, quadríplica o número de pessoas apanhadas pelo
boato.
Supondo que o boato não é desmentido, quantos dias serão precisos para que o boato se
espalhe junto de toda a população de Cabo Verde?
Escreva a função que define essa propagação.
Reflexão
⇒ Ler atentamente o
Acção
9 Ler.
problema?
⇒ De que problema se trata?
9 Problema de um boato , que pretende
saber o tempo para que a mesma chegue a
toda a população Cabo Verdiana
⇒ O que é que sabemos acerca
do tema em destaque
(população C. Verdiana)?
⇒ O que foi pedido?
⇒ O que foi dado?
9 Existem aproximadamente 510 000(INE)
Obs:(Uma previsão)
9 O tempo para que esse boato chegue a
toda a população de C. verde.
9 A relação que existente entre o dia e o
numero de pessoas que a informação
chegue junto da mesma.
⇒ Existe um algoritmo pré
estabelecido para resolver o
problema?
9 Não.
30
⇒ Será que é necessário
9 Sim.
utilizar variáveis?
9 d, para representar o número de dias e p o
⇒ Como? Para quê?
número de pessoas ambas desconhecidas.
⇒ Que modelo?
9 Uma tabela ,uma função ...
⇒ Escreve as relações.
9 Ver (1)
⇒ Que modelo Matemático
9 Função exponencial.
traduz o problema?
9 Sim.
⇒ Esse modelo traduz o
significado do problema?
9 Sim.
⇒ Pode se comprová-lo no
enunciado do problema?
9 Fazendo substituição para alguns
⇒ De que forma?
números.
⇒ Existe outra forma de
9 Sim
representar o problema ?
9 Ver(2)
⇒ Tira conclusões e formula
uma resposta
Reflexão/acção
(1)
Nº de dias
Nº de pessoas
_______________________________________________________________-
1
P=1
= 40
=1
2
P=1× 4
= 41
=4
3
P=1× 4× 4
= 42
=16
4
P=1× 4× 4× 4
= 43
=64
5
P=1× 4× 4× 4× 4
= 44
=256
…..
………………
….
…..
31
Designado por d o número de dias e por P o número de pessoas, podemos definir a
função que caracteriza essa propagação do boato. P = 4d −1
Aparentemente parece que vai demorar um certo tempo, mas ….
D (nº de dias)
N (nº de pessoas)
…..
……
6
1 024
7
4 096
8
16 384
9
65 536
10
262 144
11
1 048 576
12
4 194 304
13
16 777 216
No dia 11 de Abril já todos os Cabo-verdianos foram apanhados pelo boato. (2)
32
Propagação de uma praga
Ao combater uma praga de insectos com um novo insecticida, verificou-se que, em cada
dia, o número de insectos decresce 50%. Supondo que o número inicial de insectos foi
estimado em 1000000, define a função que traduz a variação do número de insectos em
função do tempo.
Ao fim quanto tempo deixará de haver insectos?
Reflexão
⇒ Ler atentamente o
Acção
9 Ler.
problema?
⇒ De que problema se trata?
9 Definir uma função que traduz a variação de
insectos em função de tempo.
⇒ O que foi pedido?
9 A função que traduz a variação do número
de insectos em função do tempo e
determinar o tempo necessário para que essa
praga terminasse.
⇒ O que foi dado?
9 Foi dado o número de insectos e a relação
entre dia e número de insectos infectados
pela insecticida.
⇒ Existe um algoritmo pré
9 Sim , Ver(9).
estabelecido para resolver
o problema?
⇒ Será preciso usar
9 Sim.
variáveis?
⇒ Para representar o quê?
9 Para representar o tempo (d) e numero de
insectos infectado (I).
⇒ Já resolveu problemas
9 Sim.
semelhantes?
⇒ Que relação existe entre
as variáveis?
9 É que o número de insectos diminui por dia
50%.
33
⇒ Pode se traduzir relação
9 Sim.
para a linguagem
Matemática?
9 Função exponencial.
⇒ Que modelo Matemático
pode se utilizar.
⇒ Como é que se processa a
9 Numa tabela porque já se resolveu um
problema parecido.
organização da
informação ?
9 Sim
⇒ É possível usar algum
Calculadora gráfica ou computadores.
instrumento? Qual é o
instrumento?
9
⇒ Analisa o procedimento
Ver (3)
que utilizou e dê a
resposta.
Reflexão/acção
Sabemos que, cada dia, o número de insectos é metade do número do dia anterior. Se
representarmos por d o número de dias e por l o número de insectos, a função fica
definida por: l = 1000000 × 0,5d
Podemos construir uma tabela.
Nº de dias
Nº de insectos
0
1000 000
1
500 000
2
250 000
3
125 000
4
62 500
5
31 2509
…..
…..
20
0.95
Verifica que, à medida que os dias passam, o número de insectos decresce rapidamente.
Trata-se de uma situação de decrescimento geométrico ou exponencial.
34
Embora teoricamente o número de insectos nunca chegue o zero, podemos considerar
que a praga é erradicada ao fim de 20 dias.
l = 1000000 × 0,520 ≈ 0.95
(3)
Juros
1-Um banco Exponencial Cabo-verdiano, é um banco muito especial. Sobre qualquer
depósito a prazo dá 9% de juro ao ano.
Supõe que fazes um depósito a prazo de 1000 contos no BCV. Qual vai ser o teu capital
acumulado ao fim de um ano?
E se em vez de dar 9% de 12 em 12 meses, o BCV oferecer mensalmente 9/12%?
Qual vai ser, neste caso, o capital acumulado ao fim de um ano?
Terás vantagem em adoptar esta segunda modalidade?
Reflexão
Acção
⇒ Ler atentamente o problema?
9 Ler.
⇒ De que problema se trata?
9 Problema de juro.
⇒ O que foi pedido?
9 Determinar o capital açulado de acordo
com a taxa de juro pré estabelecida, para
alem disso comparar as duas propostas.
⇒ O que foi dado?
9 A taxa de juro e saldo contabilístico.
⇒ Existe alguma fórmula que
9 Sim.
permite resolver o problema?
⇒ Qual é a formula?
9 C = D × (1 + j ) , j-juros e m-meses
⇒ Já resolveu problemas
9 Sim.
m
semelhantes?
⇒ Existe um único modelo para
a resolução do problema
referido?
9 Não.
35
⇒ Identifica alguns modelos.
9 Função exponencial, regra de três
simples etc.
⇒ Como calcular capital
9 Ver(4)
acumulado?
⇒ A solução é lógica.
⇒ Analisa, formula a resposta .
9 Ver(4)
Reflexão/acção
•
Juro capitalizado uma vez por ano
Como o juro é de 9%, o depósito vai ser multiplicado no fim do ano por (1+0,09) ou
seja, 1,09. Obtém-se assim:
C = D × 1, 09 = 1000 × 1, 09 = 1090 contos
•
Juro capitalizado 12 vezes por ano
Como o juro é de 9/12%, e vai ser capitalizado 12 vezes durante o ano, o depósito
vai ser multiplicado mensalmente por (1+0,09/12), ou seja, 1,0075. Obtém-se assim,
ao fim de um ano:
(4)
12
⎛ 0, 09 ⎞
12
C = D × ⎜1 +
⎟ = 1000 × 10075 = 1093 contos
12 ⎠
⎝
Nesta segunda modalidade ganha-se mais 3 000$00, aproximadamente.
36
2- Em 2006, o João depositou 100 contos à taxa anual de 15%. Supondo que a taxa
anual não se alterou, que capital terá no final do ano 2016?
Utilizando o procedimento acima citado a resolução se processa da seguinte forma:
Registe, numa tabela, o valor do capital do João desde 2006
Ano
Nº de anos de depósito
Capital (em contos)
2006
0
100
2007
1
100+0,15 × 100=100 × 1,15=115
2008
2
100 × 1,152 =132,25
2009
3
100 × 1,153 ≈ 152, 088
2010
4
100 × 1,154 ≈ 174,901
….
….
…..
2016
10
100 × 1,1510 ≈ 404,556
R: Ao fim de 10 anos, o João terá cerca de 405 contos. A expressão que permite saber o
capital do João ao fim de t anos é dada por C (t ) = 100 × 1,15t . Trata-se de uma função
exponencial de base superior a 1.
De um modo geral, um capital Q que se deposite num banco a uma taxa de 15% ao ano
1
⎛ 0,15 ⎞
t
converte em C = Q ⎜1 +
⎟ ao fim de um ano e em C = Q × 1,15 ao fim de t anos.
1
⎝
⎠
37
Idade de um fóssil
Para saber a idade de um fóssil os cientistas determinaram a quantidade do isótopo
Carbono 14 nele contido. A função C (t ) = Qe
−
t
5760
indica a quantidade de carbono 14
que resta no fóssil decorridos t anos desde a morte do animal ou planta até à
actualidade. Na fórmula, Q representa a quantidade do isótopo à data da sua morte.
Para um fóssil em que Q=1000 g, qual é a quantidade de Carbono 14 que nele pode ser
detectada passados 1000, 2000 e 10 000 anos?
Acção
Reflexão
⇒ Ler atentamente o problema?
9 Ler.
⇒ De que problema se trata?
9 Problema de idade de um fóssil.
⇒ O que é pedido?
9 Determinar a quantidade de Carbono 14
que no referido lhe tem detectado num
determinado tem .
9 A função que define a quantidade de
⇒ O que é dado?
Carbono 14 no fóssil em estudo num
determinado período de tempo.
9 Sim.
⇒ Os dados são suficientes?
⇒ Como
pode
organizar
a
9 Numa tabela.
informação?
9 Sim , a calcadora gráfica e computadores.
⇒ É necessário algum material
de apoio se sim indica-o?
9 Ver (5)
⇒ Analisa as informações e tira a
conclusão.
9 Ver (5)
38
Reflexão/acção
Para esta situação a função fica definida por C (t ) = Qe
−
t
5760
.
Através deste quadro podemos analisar o comportamento da função.
T (anos)
Quantidade de 14C (gramas)
0
1000
1000
840,6
2000
706,6
3000
594
4000
499,4
5000
419,8
6000
352,9
7000
296,6
8000
249,4
9000
209,6
10 000
176,2
…………
…………..
R: A função é, pois decrescente e ao fim de 10 000 anos restam apenas cerca de
176g dos 1000g de Carbono 14 inicial, pode também observar-se este
graficamente (Utilizando a calculadora grafia)
39
Temperatura
4-Na pastelaria “Só doce” a temperatura ambiente é constante. Se a temperatura, em
graus centígragos, de um café servido nessa pastelaria, t minutos após ter sido colocado
na chávena, for dada por f (t ) = 25 + 50e −0,05t , t ∈ [ 0, +∞[ (e-número de Neper).
4.1-Determina a temperatura do café no instante em que é colocado na chávena.
4.2-Ao fim de que tempo a temperatura do café é de 50ºC?
4.3-Qual a temperatura ambiente? Justifica.
Reflexão
Acção
Acção
⇒ Ler atentamente o problema.
9 Ler.
⇒ De que problema se trata?
9 Problema de temperatura que é
dada a expressão que define a
mesma num dado intervalo de
tempo.
⇒ O que é dado?
9 A expressão que define a situação
em causa e o intervalo tempo.
⇒ O que é pedido?
9 Determinar a temperatura no
instante que é colocado na
chávena, o tempo que a
temperatura do café é de 50ºC e a
temperatura ambiente.
⇒ É necessário utilizar as
variáveis ou já existe uma
expressão que define a
9 Não, há uma expressão que define
a situação que é
f (t ) = 25 + 50e −0,05t , t ∈ [ 0, +∞[
situação?
⇒ Identifica o tempo que o
café é colocado na chávena.
9 t=0.
40
⇒ Faça a concretização da
9 Ver(6)
variável para t=0 e analise a
situação.
⇒ Que modelo Matemático
9 Função exponencial e equação
exponencial.
traduz a situação (4.2)
⇒ Resolve a condição.
9 Ver(7)
⇒ É necessário algum
9 Tabela logarítmica ou calculadora
gráfica.
instrumento?
⇒ O resultado transcreve a
9 Ver(7.1)
situação?
⇒ Organiza a tua resposta.
9
⇒ Existe um algoritmo
9 Não
Ver(7.1)
preestabelecido para a
situação (4.3).
⇒ Que relação existe entre a
9 Quando
o
tempo
aumenta
temperatura ambiente e a
indefinidamente a temperatura tente
temperatura do café ?
estabilizar a temperatura ambiente.
⇒ Organiza a sua resposta e
faça verificação.
Ver
(7.2)
Reflexão/acção
4.1-
Resolução
Dados
t=0 ; a expressão f (t ) = 25 + 50e −0,05t , t ∈ [ 0, +∞[ Calculemos
f (0) = 25 + 50e −0,05×0 =
= 75
R:A temperatura do café no instante em que é colocado na chávena é de 70ºC
( 6)
41
4.2Dados
t=0 ; Temperatura f (t ) =50ºC; a expressão f (t ) = 25 + 50e −0,05t , t ∈ [ 0, +∞[
Resolução
50 = 25 + 50e −0,05t ⇔ 50 − 25 = 50e −0,05t ⇔
25
1
1
⇔ e −0,05t =
⇔ 0,05t = ⇔ 2 = e0,05t ⇔
50
2
e
⇔ ln 2 = 0, 05t ⇔ t ≈ 14mn
(7)
Verificação
f (50) = 25 + 50e −0,05×50 = 25 + e−2,5 = .........
R: O tempo é aproximadamente 14 minutos .
4.3-Calculemos lim f (t ) = lim ( 25 + 50e −0,05t
x →+∞
x →+∞
(7.1)
) = lim ⎛⎜⎝ 25 + 50 × e 1
x →+∞
0,05t
⎞
⎟ = 25
⎠
R: A temperatura ambiente é de 25ºC
(7.2)
42
Problemas de optimização
1- A função f (t ) = 1000e1,2t traduz o crescimento de uma certa população de insectos (t
representa o tempo em semanas).
Mostra que a variação da função é proporcional à própria função. Qual é o significado
desta relação?
REFLEXÃO
⇒ Ler atentamente o enunciado.
ACÇÃO
9 Ler.
⇒ De que problema se trata?
9 Problemas de optimização ou seja
⇒ O que é pedido?
crescimento da população de insectos.
9 Para mostrar que f `(t ) = 1, 2 × f ( x) .
⇒ O que é dado?
9 E dado a expressão que traduz o
⇒ Quais são condições?
crescimento da população de insectos.
9 A variação da função é proporcional a
⇒ É necessário usar variáveis?
mesma.
9 Não.
⇒ Existe
um
algoritmo
9 Sim.
preestabelecido para a referida
situação?
9 Primeiro determinar a 1ª derivada , 2º
⇒ Qual é o algoritmo?
estudar o sinal da 1ª derivada .
f (t ) = Pe kt ( K > 0)
⇒ Executar
e
resultado obtido.
verificar
o
9 Ver(8)
⇒ Dar a resposta.
Idem
Reflexão/acção
43
Podemos começar por considerar a função f como a composta de duas funções.
f (t ) = f (u ) = 1000eu
Utilizando
a
derivada
em que u (t ) = 1, 2t
da
função
composta
obtém-se:
f `(t ) = f `(u ) × u = ⎡⎣1000eu ⎤⎦ × (1, 2t ) = 1000 × ⎡⎣eu ⎤⎦ × (1, 2t ) =
`
`
`
= 1000eu × 1, 2 = 1, 2 × f (t )
Como f `(t ) > 0 para qualquer valor de t ∈
+
, a função f é crescente em todo o seu
domínio.
Por outro lado, como f `(t ) = 1, 2 × f (t ) , quanto maior for a população maior vai ser a taxa de
variação. Por exemplo:
t = 1 semana
f (1) = 1000e1,2 ≈ 3320
f `(1) = 1, 2 × 1000e1,2 ≈ 3984
Ao fim de uma semana existem cerca de 3320 insectos a taxa de variação é de 3984.Com a
população a aumentar continuamente e a taxa de variação proporcional a ela, tem-se, passada
outra semana:
t = 2 semana
f (2) = 1000e 2,4 ≈ 11023
f `(2) = 1, 2 × 1000e 2,4 ≈ 13228
Ao fim de duas semanas a população já aumentou para 11023 e a taxa de variação aumentou
para 13228.
Assim podemos concluir que à medida que a população aumenta, a taxa de variação também
aumenta, de tal modo que esta é directamente proporcional ao aumento da população.
f `(t ) = 1, 2 × 1000e1,2t
Existe muitos fenómenos naturais, como por exemplo o crescimento de populações que
podem ser descritos por funções do tipo f (t ) = Pe kt ( K > 0) em que t designa o tempo e P a
44
população inicial. A variação de qualquer função deste tipo é proporcional à própria função,
ou seja, f `(t ) = K × f (t )
(9)
Utiliza o mesmo procedimento acima referido para resolver o mesmo problema
2-O número de peixes de um lago foi estimado em 500, sendo o seu crescimento populacional
dado pela função logística p(t ) =
10000
1 + 19e
−
t
5
, em que t representa o tempo (em meses).
2.1-Qual é a taxa de variação ao fim de um mês? E ao fim de 10 meses?
2.2-Em que momento a taxa de variação é mais rápida?
2.3-A longo prazo, qual vai ser a evolução da população?
Sugestão de resolução
Esta função tem como domínio
+
, não tem zeros e é contínua em todo o seu domínio.
Vamos calcular a derivada da função a fim de responder às duas primeiras questões.
Utilizando a regra do quociente:
`
t
t
t
− ⎞
− ⎞
− ⎞
⎛
⎛
⎛
5
5
5
(10000 ) ⎜1 + 19e ⎟ − 10000 ⎜1 + 19e ⎟ −10000 ⎜ −3,8 × e ⎟
⎝
⎠
⎝
⎠ =
⎝
⎠=
p`(t ) =
t 2
t 2
− ⎞
− ⎞
⎛
⎛
⎜ 1 + 19e 5 ⎟
⎜1 + 19e 5 ⎟
⎝
⎠
⎝
⎠
`
=
38000 × e
−
t
5
t
− ⎞
⎛
5
⎜1 + 19e ⎟
⎝
⎠
2
Como p`(t ) > 0∀t ∈
•
+
, a função p é crescente em todo o seu domínio.
Ao fim de um mês:
p`(1) ≈ 114
Neste momento, os peixes reproduzem-se à razão de 114 (por mês).
•
Ao fim de dez meses:
p`(10) ≈ 403
Neste momento, a taxa de reprodução é de 403 peixes (por mês).
Aparentemente a função cresce cada vez mais rapidamente, ou seja, a taxa de variação dos
peixes é cada vez maior. Com uma calculadora gráfica podemos verificar que esta suposição
não é correcta.
45
Pode observar-se que o gráfico apresenta um ponto de inflexão, aproximadamente para t=14.
Isto significa que vai existir um momento em que a taxa de variação, embora sempre positiva,
deixa de aumentar e começa a diminuir. Para sabermos quando atinge o seu valor máximo
podemos procurá-lo com a calculadora gráfica a partir da representação da função p ou sua
derivada:
Para t ≈ 14, 72 a função derivada é máxima e aproximadamente igual a 500, ou seja, a taxa de
variação nesse momento é de 500 peixes (por mês).
Podíamos também ter obtido este valor calculando a segunda derivada.
`
t
t
t
⎡
⎤
− ⎛
− ⎞⎡
− ⎤
5
5
5
t
⎢
⎥
e
1
19
e
0,
2
3,8
e
+
−
+
−
⎜
⎟⎢
⎥
⎢
⎥
e 5
⎝
⎠
⎣
⎦
p``(t ) = 38000 × ⎢
⎥ = 38000 ×
t 2
t 4
− ⎞ ⎥
− ⎞
⎛
⎢⎛
5
5
⎜1 + 19e ⎟
⎢ ⎜1 + 19e ⎟ ⎥
⎝
⎠
⎝
⎠
⎣
⎦
Calculando os zeros da segunda derivada ficamos a saber o valor máximo da primeira.
p``(t ) = 0 quando −0, 2 + 3,8e
Resolvendo a equação:
−
t
5
=0
46
−0, 2 + 3,8e
−
t
5
=0⇔e
−
t
5
=
0, 2
t
⎛ 0, 2 ⎞
⎛ 0, 2 ⎞
⇔ − = log ⎜
⇔ t = −5 × log ⎜
⎟
⎟ ⇔ t ≈ 1472
3,8
5
⎝ 3,8 ⎠
⎝ 3,8 ⎠
Da observação do gráfico da primeira derivada podemos ainda constatar que, a longo prazo, a
taxa de variação vai aproximar-se do valor 0. Tal significa que a população de peixes do lago
poderá estabilizar. Podemos ter confirmação determinando o limite da função quando
x → +∞ .
lim
x →+∞
10000
1 + 19e
t
−
5
=
10000
= 10000
1 + 19 × 0
O número de peixes vai aproximar-se de 10000. O gráfico da função tem uma assimptota
horizontal de equação y = 10000 . Aliás, qualquer população animal tende a ter o seu
crescimento condicionado por vários factores (espaço, falta de alimento, concorrência de
outras espécies, etc.).
47
3.7.2- Problemas propostos
1-Sabendo que uma colónia, constituída inicialmente por 100 000 bactérias, cresce a uma taxa
de 6,8% por minuto, qual o número de bactérias ao fim de 1 hora?
2-O Pedro aos 15 anos, resolveu aplicar todas as suas economias -1250euros – numa conta a
prazo. O banco garantiu-lhe até aos 21 anos um juro anual de 7%
2.1- Descreve a evolução financeira do Pedro naquele período de tempo.
2.2-Traduz graficamente esta situação.
3-No lanchonete do Carlos, que se mantêm à temperatura ambiente constante de 18ºC, um
galão quente a 70ºC.
4-Sabendo que a temperatura em ºC, é dada, em instante, em função do tempo decorrido após
a saída do galão, por T (t ) = A + B • e − ct (A e B ,c constantes positivos , t em minutos).
.4.1-Determina A e B e c (c com 4 casas decimais) sabendo que ao fim de 10m a temperatura
do galão é 45ºC.
4.2-Qem pediu um galão quente mas deseja bebê-lo a 35ºC quanto tempo terá que esperar?
5-Numa população do litoral desde 1980 que se estuda, ano a ano, o número de habitantes
existentes e verificam que este se ajuste à lei: N = 400 × 1, 2t (t – número de anos com inicio
em 1980).
5.1-Qual a população em 1980?
5.2- Qual a população em 1985? E em 1995?
5.3-Quantos habitantes terão em 2009?
6-Numa população do interior foi feito um estudo análogo e verificou-se que a lei é
N = 1200 × 0,85t .
6.1-Qual a população em 1980, em 1985 e em 1995?
6.2-Qual é a população prevista para o ano 2008?
7-Uma população tem uma taxa de crescimento de 2% ao ano desde 1900.
7.1-Que função exponencial traduz o número de habitantes que em 1900 era de 350.
7.2-Quantos habitantes tinha em 1950? E quantos terá em 2010 se continuar a mesma lei?
48
7.3-Quantos anos demora nestas condições a duplicar o número de habitantes?
7.4- Mostra que o número de habitantes pode ser dado por uma expressão do tipo y = a × ebx
8- Um ser vivo tem por grama de Carbono 10−6 gramas de Carbono 14 ( C14 ). O Carbono 14
inicia a desintegração após a morte e a massa reduz-se a metade em 5500 anos (período de
semidesintegração do Carbono14).
8.1-Qual a expressão que dá a quantidade de Carbono 14 por grama de Carbono ao fim de t
anos?
8.2-Ao fim de quantos anos a quantidade de Carbono 14 se reduz a ¼?
8.3-Num fóssil de 3000 anos que quantidade de Carbono 14 existirá em cada grama de
Carbono?
8.4-Analisou-se um bocado de osso encontrado numas escavações e havia 5 × 10−6 gramas de
Carbono em 100g de Carbono. Que idade terá o osso?
49
IV-PARTE
4-TRABALHO DE CAMPO
4.1-Metodologia
Este estudo foi feito no âmbito da obtenção do diploma de licenciatura em ensino de
Matemática, no qual se baseou numa experiência de trabalho com três turmas de Matemática
do 12º ano de escolaridade na Escola Secundária de São Miguel, tendo como proposta
pedagógica a valorização do processo de ensino-aprendizagem centrado na resolução de
problemas utilizando o modelo de resolução função exponencial.
Foi considerado como objectivo fundamental do estudo a análise da evolução dos alunos em
relação a capacidade de resolver problemas e principalmente as dificuldades dos alunos na
resolução dos problemas, utilizando o modelo de resolução função exponencial.
Os trabalhos de campo realizado em Maio do ano lectivo 2006/2007 estiveram envolvidos
todos os alunos do 12º ano da área Económico e Social e os alunos da área Ciências e
Tecnologia. Ao longo da experiência, a distribuição semanal das horas lectivas foi 2+1+1. De
uma forma geral nas aulas de duas horas, os alunos trabalharam em grupos de 4 ou de 6 na
resolução das fichas de trabalho que lhes eram propostas nas aulas de uma hora a partir das
actividades exploradas em grupo, o professor formalizou alguns conceitos e regras, organizou
sínteses e propôs exercícios de práticas individuais.
A proposta pedagógica, definida pelo investigador das turmas partiu da aceitação de alguns
princípios gerais. E que destacamos os seguintes:
•
a resolução de problemas é importante na formação Matemática dos alunos;
•
o ensino da Matemática deve decorrer num ambiente de trabalho que estimule o aluno
a envolver-se activamente na construção de conhecimento;
50
•
a função exponencial é um conceito importante na consolidação dos conceitos
ministrados;
•
o trabalho em pequenos grupos, na medida em que permite o desenvolvimento de
capacidades como argumentar e criticar, expor as suas ideias e ouvir as dos colegas,
comparar estratégias e soluções, é uma experiência que deve ser proporcionada aos
alunos;
•
na exploração de situações que favoreçam uma participação activa dos alunos é
importante dar tempo para que estes possam desenvolver as actividades que lhes são
propostas e reflectir sobre elas.
A natureza do tema em estudo, leva-nos a investigar um contexto de práticas complexas e
subjectivas, por isso, optámos pelas metodologias de observação directa, técnicas de recolha de
dados por inquéritos de questionários e entrevistas, de modo a termos possibilidades de
compreender com uma margem mais alargada o tema.
Para o efeito, elaborou-se uma ficha de questionário, que é constituída por questões abertas,
semiabertas e fechadas, destinados aos alunos do 12º ano de escolaridade da escola
Secundária de São Miguel.
A dada ficha tem questões de categorias diferentes, englobando treze parâmetros e um item e
esses parâmetros têm três questionários semi-fechados destinados aos alunos e também nove
perguntas fechadas e duas abertas respectivamente;
O Inquérito foi aplicado aos alunos do 12º ano de escolaridade na escola Secundária de São
Miguel, alunos referentes as turmas de Económico e Social 1 , Económico e Social 2 e
também na turma de Ciências e Tecnologia 1. Esse inquérito vem na sequência de
comparação e complementaridade dos resultados recolhidos nas outras técnicas utilizadas,
tendo em conta que, os alunos, sendo autores principais do processo de ensino aprendizagem,
podem revelar aspectos importantes da vida escolar, e permite ainda, recolher maior número
de dados possíveis para a pesquisa.
A escolha dessas técnicas justificam-se, na medida em que, permitem um tratamento mais
sistematizado dos dados, obtendo maiores números de dados possíveis em menos tempo, e
ainda facilita, muito o tratamento dos dados disponíveis.
51
A escola secundária de São Miguel tem aproximadamente 150 anos no 12º ano, sendo assim
87 tem a Matemática e os restantes são da área Humanística.
O inquérito com os alunos foi feito nas turmas com os alunos distribuídos em cada sala, em
momentos diferentes e reunidos num mesmo espaço, responderam às questões propostas
depois de lida e explicadas pelo inquiridor; Os alunos receberam as fichas de inquérito,
preencheram-nas, sob a orientação do inquiridor que prestou esclarecimentos sempre que
necessários e de seguida recolheu as fichas preenchidas, agradecendo a colaboração de todos.
Depois de se ter procedido à recolha das fichas de entrevistas abertas e semiabertas, procedeuse, a leitura e análise das respostas, de acordo com as categorias, que de seguida, foram
sistematizada num quadro com base nas tendências e afinidades das respostas de cada
entrevistado.
Os inquéritos feitos aos alunos, receberam um tratamento estatístico através do recurso aos
programas informáticos SPSS e Excel para Windows; Após obtenção dos ficheiros finais
procedeu-se à análise e tratamento das informações disponíveis, com base nos dados
recolhidos por categoria, contendo uma síntese final de todos os dados referentes a resolução
de problemas.
No entanto, pode-se referir que, a utilização dessas técnicas permitem recolher de forma
eficiente e eficaz, importantes informações sobre as visões, as percepções, e os conhecimentos
dos principais intervenientes, sobre o assunto em questão; oferecendo maiores
disponibilidades dos dados para analise e tratamento.
52
4.2-Recolha e tratamento de informações
4.2.1- Organização e reflexão sobre as respostas
O questionário foi aplicado numa amostra de 50 alunos. Desses, 44% são do sexo masculino e
56% do sexo feminino, sendo que 56% são da área Económico e Social e 44% da área
Ciências e Tecnologias, respectivamente. Esses alunos apresentaram as suas ideias acerca do
que entendiam por um problema matemático, findo ao qual, a título de exemplo, procedemos
à resolução de problemas. Aproveitamos para questionar os alunos a cerca do gosto pela
resolução de um problema matemático, relação entre os problemas resolvidos e a sua
aplicação no dia-a-dia e algumas dificuldades na resolução desses problemas, como constam
dos itens seguintes:
Nas questões abertas e semiabertas obtivermos as seguintes respostas:
No que tange a definição de problema matemático, todos os entrevistados revelaram que têm
ideia da definição de um problema matemático. As definições dadas pelos alunos foram de
encontro, na sua maioria, às ideias a seguir apresentadas:
•
problema matemático é aquele que devemos ler primeiro interpretar e, só depois,
responder às questões;
•
problema matemático é quando temos um enunciado na linguagem corrente e que
temos que o transformar na linguagem Matemática e, depois, resolvê-las, utilizando
algoritmo;
•
são conjuntos de dados que nos são fornecidos para podermos resolver.
•
é aquele que nos ajuda a resolver segredos matemáticos;
•
um problema refere-se a algo com que uma pessoa se depara, ocultando ou
escondendo algo mais que está por detrás;
•
É uma tarefa na qual o indivíduo ou grupo se confronta com a necessidade de
encontrar a solução, não possuindo um procedimento directamente acessível que
garanta a solução.
Quanto aos questionários fechados, como se sabe, houve nove questões fechadas. No que
tange ao número de vezes que os entrevistados resolvem um problema matemático, 22%
resolvem, no máximo, quatro vezes e 26% resolvem problemas superiores a quatro vezes e
53
não superiores a oito vezes e os restantes dos entrevistados resolvem problemas superiores a
oito vezes.
“Número de vezes que os alunos andam a resolver problemas”
Número de
Vezes
0-4
Frequência Percentagem
11
22.0
4-8
13
26.0
Superior a 8
Total
26
50
52.0
100.0
No que se refere ao grau de dificuldade dos problemas resolvidos nas turmas, 72%
consideram que esses problemas são fáceis e 14% responderam que são difíceis e os restantes
mostraram-se indiferentes.
Dado que os problemas levados para turma tinham como objectivo facilitar a compreensão do
conteúdo, elaborou-se um questionário concordemente. 58% desses alunos responderam que
facilitam a compreensão dos conceitos envolvidos e 48% responderam que não.
Quanto à justificação, os alunos responderam que os problemas resolvidos lhes têm ajudado
na compreensão e solidificação do conceito de função exponencial e argumentaram de
seguinte forma:
Resolver qualquer problema facilita a resolução de outros problemas, mesmo que não seja de
Matemática, tendo em conta que há problemas, envolvendo função exponencial, que estão
ligados a Química. Também, conforme disseram, ao resolver problemas, há propriedades que
a partir daí ficam mais claros devido a tanta prática. Acrescentaram ainda que resolver
problemas leva os alunos a lembrar dos conteúdos trabalhados nos trimestres passados, ajuda
os alunos a ampliar a visão das coisas e, consequentemente, o aluno fica mais ágil na
resolução de exercícios, envolvendo a função exponencial. Um problema relacionado com a
questão em estudo contribui para desenvolver a forma de pensar dos alunos, desenvolve o
espírito crítico em relação ao tema em estudo e isso reflecte-se na aprendizagem.
54
“Os problemas resolvidos são fáceis?”
Resposta
Frequência Percentagem
Sim
36
72.0
Não
7
14.0
Nem um nem
outro
Total
7
14.0
50
100.0
“Os problemas resolvidos facilitam na compreensão de outros conteúdos?”
Resposta Frequência
Percentagem
Sim
29
58.0
Não
21
42.0
Total
50
100.0
No que diz respeito às resposta dos alunos acerca da resolução de problemas por cada tema,
40% dos alunos responderam que o professor de Matemática apresenta muitas vezes
problemas para serem resolvidos em cada tema em estudo, 50% responderam que o professor
apresenta problemas às vezes, 6% responderam que quase nunca e 4% responderam que o
professor nunca lhes apresenta problemas para serem resolvidos nos temas estudados.
“Os temas estudados costumam ser aplicados pelo professor na resolução de problemas?
Dados
Frequência Percentagem
Muitas vezes
20
40.0
As vezes
25
50.0
Quase nunca
3
6.0
Nunca
2
4.0
Total
50
100.0
Questão: “Você gosta de resolver os problemas matemáticos?” 76% dos alunos entrevistados
responderam que gostam de resolver problemas e 24% responderam que não.
Apesar de algumas dificuldades dos alunos na resolução de problemas, de acordo com as
respostas fornecidas, muitos gostaram de resolver problemas e até justificaram que quando se
resolve um problema, o aluno reflecte mais e isso influencia no entendimento de cada tema
em estudo; Alguns até mesmo responderam que gostam de resolver problemas para poder
55
fazer mais prática e também para poder ter mais oportunidade de questionar. Ainda um outro
factor que leva aos alunos a gostar de resolver problemas tem a ver com o facto de poder
entender melhor os conteúdos e fixar melhor a matéria em resultado de aplicabilidade na
resolução de problemas. Por último, acharam que resolver problemas os ajuda a ter mais
clareza da realidade, ou seja, que a resolução de problemas é uma forma de se ver a ligação da
Matemática com a realidade.
Quanto aos que responderam negativamente à questão, justificaram a escolha com o pouco
gosto que têm pela disciplina, o não entendimento dos conteúdos e a demora para se chegar a
um resultado, que muitas vezes acaba por ser incorrecto.
“Gosto pela resolução de problemas”
Resposta Frequência
Percentagem
Sim
38
76.0
Não
12
24.0
Total
50
100.0
A resposta dos alunos acerca da forma como o professor lhes tem apresentado o tema função
exponencial, 56% responderam que gostam e entendem; 12% não gostam, mas entendem;
28% responderam que sim; mas não entendem; 4% dos alunos responderam que não gostam
da forma como o professor lhes apresentaram o tema e que não entendem.
“ Gosto pela forma como o professor apresenta a função exponencial”
Resposta
Frequência Percentagem
Sim entendo
28
56.0
Não mas entendo
Sim mas não
entendo
Não
6
14
12.0
28.0
2
4.0
Total
50
100.0
Quanto a aplicabilidade do conteúdo no dia-a-dia, 86% dos entrevistados responderam que
sim e 14% responderam que não. Em relação ao tema em estudo, os referidos alunos
argumentaram de forma semelhante, isto é, a maioria dos inqueridos justificaram que o
conceito tem aplicabilidade na vida quotidiana relativamente aos problemas de evolução de
56
uma habitação, propagação de uma doença, cálculo de juros e também propagação de um
boato… etc.
“Aplicabilidade do conteúdo no dia-a-dia”
Resposta Frequência
Percentagem
Sim
43
86.0
Não
7
14.0
Total
50
100.0
66% dos entrevistados responderam que entendem o conteúdo mas não conseguem aplicá-lo
na resolução de problemas e 34% desses entrevistados responderam que não .
“Relação entre o entendimento do conteúdo e a sua aplicação na resolução de problemas”
Resposta Frequência
Percentagem
Sim
Não
33
17
66.0
34.0
Total
50
100.0
Dificuldades na resolução de problemas matemáticos
Como se sabe, o objectivo do trabalho é identificar as dificuldades dos alunos na resolução de
problemas, utilizando o modelo de resolução função exponencial. Para tal, eles apontaram
algumas dificuldades, tais como:
Ö
Identificar informação necessária para resolver um problema.
Ö
Seleccionar estratégias para resolver problemas.
Ö
Medir a extensão de progresso feito durante a tentativa de solução.
Ö
Implementar uma estratégia.
Ö
Determinar a aceitação dos resultados.
Ö
Entendimento do conteúdo.
Ö
Concentração.
Ö
Em entender o pedido do enunciado.
57
Ö
Transformar na potência de mesma base.
Ö
Iniciar a organização de informações.
Ö
Transformar o problema em linguagem matemática.
Ö
Equacionar o problema.
Ö
Relacionar o tema, que é função exponencial, com a resolução de problemas.
Ö
Análise de resultados.
Ö
Apresentação de solução.
58
V-PARTE
5-COONCLUSÃO E RECOMENDAÇÔES
5.1-Conclusão
A pesquisa que levamos a cabo, cujo produto final redunda a este trabalho, permitiu-nos
constatar, entre outras coisas, o que se segue:
Em primeiro lugar, ressalto a necessidade premente de abordador o tema da resolução de
problema no níveis mais baixos uma vez que, por exemplo, o professor sentir-se-á mais à
vontade em utilizar as ideias expostas na segunda parte, a saber, conceitos de problemas
matemáticos, uma vez que neste nível os problemas redundam praticamente a cálculos
algébricos;
Não esgotamos a exploração do tema, pois apenas demos um modesto contributo para a sua
clarificação, pelo que será de todo oportuno se o mesmo vier a ser aproveitado noutros níveis.
No que tange ao trabalho de campo propriamente dito, os alunos evoluíram significativamente
em relação à capacidade de resolver problemas. Ao nível do trabalho em grupo, revelaram
uma crescente facilidade em compreender os problemas, em implementar estratégias
adequadas à sua resolução e em organizar o trabalho escrito de forma adequada. Os alunos
passaram a conseguir resolver problemas, numa atitude de crescente autonomia, deixando de
solicitar qualquer ajuda.
59
Em relação à resolução de problemas individualmente, alguns alunos ainda evidenciavam
dificuldades em resolver, de uma forma correcta, os problemas apresentados. No entanto, um
grande número deles conseguia mostrar uma certa compreensão dos problemas propostos e
procurava estratégias adequadas para sua resolução.
Em relação à utilização de estratégias de resolução de problemas pelos alunos, foi também
possível observar uma grande evolução, que se deu graças à resolução de problemas por
ensaio e erro sistemático. Também foi com crescente facilidade que os alunos identificaram
padrões de distribuição numérica e que aplicaram a fórmula de recorrência na resolução de
problemas.
A função exponencial é um modelo matemático utilizado em diversas actividades,
nomeadamente, em cálculo de juros compostos e na descrição da evolução de populações. É
de grande adequação pedagógica inserir o estudo desta função num contexto de modelação
matemática.
Também foi possível observar a forma como a calculadora facilitou a persistência na
resolução de problemas. Aliviados do peso dos cálculos, os alunos “agarravam-se” à
calculadora, não desistindo perante as tentativas frustradas.
Na medida em que os alunos revelaram uma crescente facilidade em analisar as situações
apresentadas e em propor diferentes processos para a sua resolução, a solução de problemas
influenciou positivamente o processo de ensino-aprendizagem. Por outro lado, alguns
problemas, quando devidamente contextualizada a exploração de conceitos, facilitaram a sua
compreensão.
Os alunos consideram que o trabalho realizado em torno da resolução de problemas foi uma
experiência que os entusiasmou e que lhes deu uma ideia diferente da Matemática. Para a
maioria dos alunos, a resolução de problemas “ajuda a saber pensar”, facilitando assim a
compreensão dos conteúdos estudados. Para outros, embora em número mais reduzido, a
resolução de problemas é sobretudo motivadora, uma vez que entusiasma a trabalhar e a
analisar situações que podem surgir no dia-a-dia.
60
A apresentação escrita da resolução de problemas foi um aspecto em relação ao qual os alunos
tiveram algumas dificuldades. A elaboração de ensaio escrito que descreve de uma forma
clara os aspectos fundamentais que levaram à resolução de problemas revelou dificuldades
iniciais, os alunos conseguiram com mais facilidade apresentar resoluções em que registavam
o trabalho que iam realizando à medida que resolviam os problemas.
Pôde-se concluir que, em relação a muitos aspectos relacionados com a resolução de
problemas, os alunos evoluíram significativamente. Mas é importante realçar que a evolução
foi lenta e implicou trabalho e envolvimento de todos.
Finalmente, parece particularmente significativo o facto de a maioria dos alunos ter
considerado que com as actividades desenvolvidas em torno da resolução de problema
aprenderam e aprendem a pensar.
5.2-Recomendações
A resolução de problemas é um instrumento precioso no ensino de Matemática pois, para
além de constituir um meio de consolidação de conhecimentos (e sua avaliação), também é
uma forma de introduzir novos conceitos e conhecimentos, sem se cair na resolução rotineira
de exercícios com elevada componente mecânica (memorização e aplicação directa, ou quase,
de procedimentos e técnicas).
Na aplicação desta estratégia é muito importante saber escolher o problema a propor. Os
problemas devem ser interessantes e compatíveis com o grau de conhecimento dos alunos, de
interpretação fácil, de linguagem simples, familiar e que permitam extrapolações de forma a
desafiar o "apetite" dos alunos, para que estes possam experimentar sensações, como a tensão
de resolver e desenvolver um problema e a glória da descoberta.
Se um aluno resolver determinados problemas com facilidade, sentir-se-á mais seguro ao
deparar-se com novos problemas (matemáticos ou não), enquanto que um aluno com mais
dificuldade, poderá sentir-se desmotivado e perder, inclusive, a vontade de estudar a
Matemática. Desta forma, é realmente importante e decisiva a correcta escolha dos problemas
a resolver (quer a nível matemático - estrutura e conteúdo - quer a nível de formulação -
61
linguagem, contexto, formato); o ter em conta o percurso escolar individual e colectivo dos
alunos (especialmente as dificuldades a nível do individual e do todo) e o acompanhamento
dado durante os vários processos de resolução.
Este acompanhamento é um aspecto fundamental, quando se trata de exploração de uma
tarefa como esta, visto que o professor pode (e deve) questionar o aluno, sugerindo-lhe (sem o
limitar) alguns caminhos para a resolução, deixando-lhe, no entanto, uma parte substancial do
trabalho, visto que o objectivo da resolução de um problema é não só o atingir de soluções (no
caso de existirem), mas também, e de forma marcante, o desenvolvimento de um raciocínio
sólido e autónomo.
Este apoio é, também, uma oportunidade que um professor não deve perder para se relacionar
com os alunos e lhes mostrar que um problema é um desafio divertido a ultrapassar, isto é,
que um problema é um jogo, assim como a própria Matemática o é, no qual, embora muitas
vezes não se precise mais do que papel e lápis, podemos utilizar tudo o que sabemos e tudo o
que temos à mão para o resolver: por exemplo, o uso de calculadoras, computadores, réguas,
esquadros, compassos... e até materiais produzidos pelos próprios professores e alunos.
É importante perceber que as tarefas que trazemos para a aula são sempre transformadas
pelos alunos, na medida em que eles criam significados próprios que dependem de seus
objectivos. Assim, ao invés de enfatizar as tarefas em si e esperar que tenham um
significado único e fixo, o professor deve preocupar-se em, gradualmente, aproximar os
significados criados pelos alunos àqueles pretendidos pela tarefa. Esta forma de olhar a
actividade dos alunos requer uma nova forma de comunicação e aprendizagem na sala de
aula. Ao trabalhar com as situações da balança, por exemplo, na resolução de uma
equação, seria interessante promover um formato de aula que incluísse pelo menos as
seguintes características (que devem ser adaptados pelo professor para cada ala de aula):
1. Permitir que os alunos resolvam os problemas testando hipóteses para os valores das
incógnitas (como no exemplo da secção anterior). Isso lhes dará familiaridade com o
comportamento da balança e suas relações com a Matemática.
2. Mesmo que os alunos já tenham obtido as respostas correctas com o teste de hipóteses
(uma estratégia essencialmente aritmética), devem ser incentivados a escrever equações
sobre o comportamento da balança (uma estratégia de modelagem algébrica) e, a seguir,
62
reunidos em duplas para que possam começar a compartilhar suas ideias com os colegas.
3. Devem ser convidados a registar (ou o professor deverá registar ele mesmo) todos os
tipos de expressões produzidas no quadro (incluindo as “erradas” e mesmo aquelas que
não estão escritas com símbolos algébricos).
4. Incentivar cada aluno (ou dupla de alunos) a apresentar a sua equação, explicando os
detalhes de como a construiu. Isso pode tomar muito tempo da aula, mas o
desenvolvimento dessa capacidade de construir argumentos para defender ideias é o
principal objectivo da escola em qualquer área.
5. O professor não precisa descartar as ideias erradas do ponto de vista matemático
assim que elas aparecem. É recomendável que se organize para fazer perguntas sobre
o significado das acções dos alunos, explicitando os contrastes entre as equações
produzidas e a situação em que se presencia.
6.Uma vez que os alunos tenham argumentado em favor de suas expressões (tendo,
talvez, já realizado modificações em relação a suas ideias iniciais), o professor
poderia até propor votações entre os alunos para a escolha da equação mais adequada
entre as apresentadas no quadro, a fim de tentar perceber em que direcção a maioria
da turma está a organizar a sua compreensão do problema. Cada votação solicita
novas defesas das equações mais votadas e menos votadas, introduzindo novas
questões que irão gradualmente alertando os alunos para as modelagens mais ou
menos adequadas da situação da balança. (É de realçar que o importante não é a
votação em si, mas a defesa que os alunos são capazes de fazer sobre a sua
produção.)
7. A resposta correcta não precisa ser alcançada já no primeiro problema. Aliás, diga-se de
passagem, uma resposta correcta não indica necessariamente que um aluno pensou mais
correctamente do que o outro que deu uma resposta errada! Portanto, é necessário planear
vários problemas e muitas situações, nas quais os alunos podem gradualmente exercitar sua
capacidade de construir representações matemáticas (por exemplo, equações algébricas) e
63
defender seus pontos de vista.
O trabalho do professor é fundamental e insubstituível em todos esses pontos. É assim que
estaremos criando oportunidades para o aluno aprender a construir argumentos matemáticos
para problemas e situações, a justificar suas acções e engajar-se em actividades de discussão
nas quais a Álgebra funciona como uma ferramenta de modelagem e resolução de problemas.
64
BIBLIOGRAFIA
ABRANTES Paulo/FERNANDES C. Raul, Matemática 11, Texto editora-Lisboa.
BRITO Cristiano /MARTINS Ana Cristina /CABRAL ST. Aubin Marinela, Matemática
Aplicações teóricas Volume II.
FREITAS A. César/ GOMES francelino, Matemática 11º ano de escolaridade (2ºano
complementar), TOMO1, R. Barros ,14-18-Tel864548-1194, Lisboa 1979.
FERREIRA N. Maria Augusta/MONTEIRO F. Maria Luísa Função3, Exercícios Matemática
12º-2ª parte-Porto Editora.
FERREIRA N. Maria Augusta, Matemática 8 Guia do Professor.
FERNANDES Domingos/BORRALHO António/AMARO Gertrudes, Resolução de
problemas: processos cognitivos, concepções de professores e desenvolvimento curricular
Modulo resolução de problemas matemática (projecto consolidação dos sistemas educativos).
LIMA Yolanda /GOMES Francelino; XEQMAT, Matemática 11º e 12º
Paulo/BASTOS Rita, Matemática 12 volume I
PORFÍRIO, Joana (1993). A resolução de problemas na Aula de Matemática. Lisboa: APM.
VEIRA L. Ana /BERNARDES António/ LOUREIRO Cristina/VARANDAS José Manuel
/VIANA José ;1ª Edição contraponto/rua Costa Cabral,859,4200Porto
Regulamento escolar interno do ISE-Regulamento de Trabalho de Fim de Curso. Maio de
2000.
65
66
GRÁFICOS
1-
2-
f1(x)=3x, f2(x )=5x, f3(x)=7x, f4(x)=1 e f5(x)=0,
f(x)=2x, g(x)=2x+2 e h(x)=2x, .
3- f(x)=2x, f1(x)=2x+1, f2(x)=2x+2 e f3(x)=2x+3.
67
4- f(x)=9x
5-
f(x)=(1/4)x
6-
f(x)=2x e g(x)=(1/2)x
68
69
Questionário aos alunos
Sou professor de matemática na escola secundária de São Miguel. Este questionário tem por
objectivo recolher informações sobre resolução de problemas matemáticos utilizando modelo
de resolução função exponencial.
Agradeço muito se pudesse colaborar comigo, respondendo às perguntas do questionário.
Garanto o anonimato e a confidencialidade das tuas respostas a todas as questões é muito
importante.
I- Identificação do entrevistado
1-Asinale com X a sua condição.
Sexo
Masculino
feminino
Área de estudo Económico social
C. tecnologia
Outras áreas
2-O que entendes por um problema matemático?
--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------3-Quantas vezes já resolveste um problema matemático neste ano lectivo?
Responde colocando um X a frente da opção que traduz a tua experiência.
0 a quatro vezes (0-4)
Quatro a oito vezes (4-8)
Mais do que oito vezes
4-Os problemas resolvidos na sua turma consideras que são fáceis ?
Sim
Não
Nem um nem outro
4.1-Achas que facilitam a compreensão dos conceitos envolvidos?
Sim
Não
Justifica----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
70
5-Em cada tema que estudaste, este ano lectivo, o teu professor de matemática costuma
apresentar problemas para resolveres?
Muitas vezes
Algumas vezes
Quase nunca
Nunca
6-Você gosta de resolver os problemas matemáticos?
Sim
Não
Assim -assim
Indica as razões-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------7-Quando o professor introduziu o estudo da função exponencial, entendeste com facilidade?
Sim
Não
8-Gostaste da forma como o teu professor de matemática te apresentou a função exponencial?
Não
Sim mas não entendo
Não gosto mas entendo
Sim e entendo
9-Achas que o conteúdo tem aplicabilidade na vida do dia-a-dia?
Sim
Não
Porquê-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------10-Os problemas que resolveste nas aulas tinham relação com a vida quotidiana?
Sim
Não
Porquê ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------11-Entende o conteúdo mas não consegue aplicar na resolução de problemas?
Sim
Não
Indica as razões-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------12- Você tem algum documento ou estudas só com o material que o professor dá?
---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
71
13-Demoras muito tempo a resolver problemas envolvendo função exponencial?
Sim
Não
Justifica--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- ---14-Quanto tempo demoras em resolver os problemas do tipo e quais são as suas dificuldades?
-------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------15-Achas que o tempo que o professor dá para resolver os problemas é :
Suficiente
pouco
muito
Justifica----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------16-Quando o professor resolveu os primeiros problemas ensinou vos a técnica como é que se
resolve ?
Sim
Não
Justifica---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------17-Deixe uma sugestão ou seja a melhor forma para ministrar o conteúdo e aplica-la na
resolução de problemas---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------