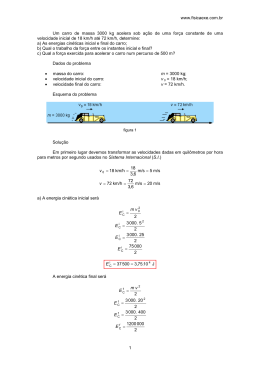
Regressão Linear
Computação – 2º Semestre 2011/2012
Caso de Estudo
Cinética Enzimática
30 Abril 2012
Regressão Linear
2
Cinética Enzimática



Os enzimas actuam como catalisadores que aceleram as reacções
químicas nas células.
Normalmente, convertem um químico, o substrato, noutro, o
produto.
A equação de Michaelis-Menten é frequentemente usada para
descrever estas reações:
vm [ S ]
v

ks  [S ]
em que v é a velocidade da reacção, vm a velocidade máxima, [S] a
concentração do substrato e ks uma constante (meia saturação)
Um modelo alternativo é a equação de Michaelis-Menten de
segunda ordem:
v [ S ]2
v
30 Abril 2012
m
k s2  [ S ]2
Regressão Linear
3
Cinética Enzimática

A figura ilustra a relação entre a velocidade e a concentração de
substrato prevista por ambos os modelos:
30 Abril 2012
Regressão Linear
4
Cinética Enzimática

Problema: Usar regressão linear nas versões linearizadas dos
modelos anteriores para o ajuste dos seguintes dados:

Solução (modelo 1):

v [S ]
Linearizar o modelo: v  m
ks  [S ]
Determinar a recta:

1 1 ks 1


v vm vm [ S ]

>> S=[1.3 1.8 3 4.5 6 8 9];
>> v=[0.07 0.13 0.22 0.275 0.335 0.35 0.36];
>> [a,r2]=linregr(1./S,1./v)
a =
16.4022 0.1902
r2 =
0.9344
30 Abril 2012
Regressão Linear
5
Cinética Enzimática
vm [ S ]
 Solução (modelo 1):
ks  [S ]
 Calcular os coeficientes do modelo:
v

1 1 ks 1


v vm vm [ S ]
>> vm=1/a(2)
vm =
5.2570
>> ks=vm*a(1)
ks =
86.2260

Resultado final:
v
5.2570[ S ]
86.2260  [ S ]
30 Abril 2012
Regressão Linear
6
Cinética Enzimática

Problema: Usar regressão linear nas versões linearizadas dos
modelos anteriores para o ajuste dos seguintes dados:

Solução (modelo 2):

Linearizar o modelo:
Determinar a recta:
vm [ S ]2
1 1 k s2 1
v 2
  
2
ks  [ S ]
v vm vm [ S ]2

>> [a,r2]=linregr(1./S.^2,1./v)
a =
19.3760 2.4492
r2 =
0.9929
30 Abril 2012
Regressão Linear
7
Cinética Enzimática

Solução (modelo 2):
 Calcular os
>> vm=1/a(2)
coeficientes do modelo:
vm [ S ]2
1 1 k s2 1
v 2
  
k s  [ S ]2
v vm vm [ S ]2
vm =
0.4083
>> ks=sqrt(vm*a(1))
ks =
2.8127

Resultado final:
0.4083[ S ]2
v
7.911  [ S ]2
30 Abril 2012
Regressão Linear
8