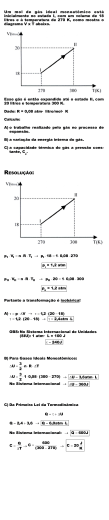
HTTP://COMSIZO.BLOGSPOT.COM/
Resolução de “Curso
Básico de Física” de H.
Moysés Nussenzveig
Capítulo 09 - Vol. 2
Engenharia Física 09 – Universidade Federal de São Carlos
11/9/2009
*Conseguimos algumas resoluções pela internet, outras foram feitas por nós.
ComSizo.blogspot.com
Capítulo - 9
1 - O tubo de vidro de um barômetro de mercúrio tem secção reta de 1 cm ² e 90 cm de
altura acima da superfície livre do reservatório de mercúrio. Num dia em que a
temperatura ambiente é de 20°C e a pressão atmosférica verdadeira é de 750 mm/Hg, a
altura da coluna barométrica é de 735 mm. Calcule a quantidade de ar (em moles)
aprisionada no espaço acima da coluna de mercúrio.
H
h
a = 1 cm² = 10-4 m2
Po = 750 mmHg = 99967,10 Pa
13,6.10 /
Temos que as pressões:
. . .
. . .
. . .
. . 0,9 0,735. 10'(
!99967,10 13,6.10 . 9,81.0,735&.
+ 1,3.10', -.
8,314. 20 273
. . . . . .
2 – Dois recipientes fechados de mesma capacidade, igual a 1 l, estão ligados um ao
outro por um tubo capilar de volume desprezível. Os recipientes contêm oxigênio,
inicialmente à temperatura de 25°C e pressão de 1 atm.
a) Quantas gramas de O2 estão contidas nos recipientes?
b) Aquece-se um dos recipientes até a temperatura de 100°C, mantendo o outro
a 25°C. Qual é o novo valor da pressão?
c) Quantas gramas de O2 passam de um lado para o outro? Despreze a condução
de calor através do capilar.
a) Pela relação dos gases ideais:
. . 32.10' . 1.013.10, . 2.10'
. . . . . . 8,314.298
+ 2,62
b) Pela relação dos gases:
. . . . . . . . /
0
/
/ 1
1
2
2 / . 1 2 1
2
/ / 2.1,013.10, 373.298
1
2 + 1,12.10, 1,11 3
298
373 298
2
ComSizo.blogspot.com
Capítulo - 9
c) Pela relação obtida no item a:
. . 32.10' . 1.12.10, . 2.10'
` ` 1,16
. 8,314.298
Portanto, a variação é:
∆ ` 1,16 2,62 + ∆ 0,15 6
* O sinal negativo do ∆m indica que houve perda de massa.
3 - Um recipiente de paredes adiabáticas é munido de um pistão adiabático móvel, de
massa desprezível e 200 cm² de área, sobre o qual está colocado um peso de 10 kg. A
pressão externa é de 1 atm. O recipiente contém 3 l de gás hélio, para o qual CV =
(3/2)R, à temperatura de 20°C.
a) Qual é a densidade inicial do gás? Faz-se funcionar um aquecedor elétrico
interno ao recipiente, que eleva a temperatura do gás, gradualmente até 70°C.
b) Qual é o volume final ocupado pelo gás?
c) Qual é o trabalho realizado pelo gás?
d) Qual é a variação de energia interna do gás?
e) Quanto calor é fornecido ao gás?
Dados:
A = 200 cm² = 2 x 10-2 m² ; m = 10 kg ; MHe = 4 g/mol ; CV = (3/2)R ∴ CP = (5/2)R
V1 = 3 l = 3 x 10-3 m³
P0 = 1 atm = 1,013 x 105 N/m²
T1 = 20°C =293 K
a)
P1 = P0 +
F
m.g
10 x 9,8
= P0 +
= 1,013 x 105 +
⇒ P1 = 1,062 x 105 N/m²
-2
A
A
2 x 10
P1.V1
= 0,13 mols
R.T1
m n.M He
ρ= =
⇒
V
V
n=
ρ = 0,174 kg/m³
b) T2 = 70°C = 343 K ; P1 = P2
V1 V2
=
⇒
V2 = 3,51 l
T1 T2
c)
W1→2 = ∫ P.dV = P ∫ dV ⇒W1→2 = P.(V1-V2) W1→2 = 1,062.105.(3,51-3).10-3
V2
V2
V1
V1
+ W1→2 =54,34 J
d)
∆U = n.CV.∆T = P.V.(R.T)-1.CV.∆T = 1,062.105.3.10-3.(293)-1.(3/2) .50
+ ∆U = 81,51 J
e)
∆U = ∆Q – W ⇒ ∆Q = 136 J
3
ComSizo.blogspot.com
Capítulo - 9
4 – Um mol de um gás ideal, com γ = 7/5, está contido num recipiente, inicialmente a 1
atm e 27°C. O gás é, sucessivamente: (i) comprimido isobaricamente até ¾ do volume
inicial V0; (ii) aquecido, a volume constante, até voltar à temperatura inicial; (iii)
expandido a pressão constante até voltar ao volume inicial; (iv) resfriado, a volume
constante, até voltar à pressão inicial.
a) Desenhe o diagrama P-V associado.
b) Calcule o trabalho total realizado pelo gás.
c) Calcule o calor total fornecido ao gás nas etapas (i) e (ii).
d) Calcule as temperaturas máxima e mínima atingidas.
e) Calcule a variação de energia interna no processo (i) + (ii).
γ = 7/5
n = 1 mol
P1 = 1 atm
T1 = 27°C = 300 K
V2 = (3/4)V1
∴ CP = (7/2)R ;
CV = (5/2)R
a)
AB:
P1.V1 = n.R.T1
⇒
V1 (3 4 )V1
⇒
=
T1
T2
T2 = 225 K
P1 P2
=
T2 T1
P2 = 1,33 atm = (4/3) atm = 1,35 x 105 N/m²
V1 = 24,6 l
BC:
b)
c)
⇒
W = WAB + WBC + WCD + WDA
mas
V
3 
 3
W = P1  − 1V1 + P2 1 − V1 = 1 (− P1 + P2 )
4
4 
 4
W = 207,67 J ≅ 208 J
WBC = WDA = 0
 1
 1
W(i) = WAB = P1 . − .V1 = 1,013.10 5. − .24,6.10 −3 = - 623,5 J
 4
 4
5
∆U(i) = n.CV.(T2 – T1) = 1. .8,314.(225,1125 − 300,15) = - 1559,655 J
2
∆Q(i) = ∆U + W
⇒
∆Q(i) = - 2183,156 J
W(ii) = WBC = 0
4
ComSizo.blogspot.com
Capítulo - 9
∆U(ii) = n.CV.(T1 – T2) = + 1559,655 J
∆Q(ii) = + 1559,655 J
∆QT = - 2183,156 + 1559,655 = - 623,50
d)
e)
⇒
P2 .V1 1,33 x 2406
=
= 399 K
⇒
n.R
1 x 0,082
P .V
1,013 x 2406 x 3
= 224,98 K
= 1 2 =
n.R
4 x 8,314
∆QT = - 624 J
Tmáx =
Tmáx = 400 K
Tmin
⇒
∆U ( i ) = −107,875 J 

∆U (ii) = +107,875 J 
Tmin = 225 K
∆U ( i ) + ∆U (ii ) = 0
5 – Um mol de um gás ideal, contido num recipiente munido de um pistão móvel,
inicialmente a 20°C, se expande isotermicamente até que seu volume aumenta de 50%.
a seguir, é contraído, mantendo a pressão constante até voltar ao volume inicial.
Finalmente, é aquecido, a volume constante, até voltar à temperatura inicial.
a) Desenhe o diagrama P-V associado.
b) Calcule o trabalho total realizado pelo gás neste processo.
a) Em AB:
. . . .
3
2
. 2
3
3
2
3
7 . . . ln =2 > 1 2
3
2
b) Temos que o trabalho é dado por:
7 789 79:
3
2
3
. . . ln =2 > 11 2
3
2
3
1
3
1
. . . ln =2 > . . 1 2 8,314.293,15 1ln 1 2 2
3
2
3
+ 7 176 ?
5
ComSizo.blogspot.com
Capítulo - 9
6 – 0,1 mol de um gás ideal, com CV = (3/2)R,
descreve o ciclo representado na fig. no planto
(P, T).
a) Represente o ciclo no plano (P, T),
indicando P (em atm) e V (em l) associados aos
pontos A, B e C.
b) Calcule ∆W, ∆Q e ∆U para os
processos AB, BC, CA e o ciclo.
a)
P (atm)
A
C
B
V(l)
b) Processo AB:
W = n.R.T.ln(VB/VA) = 0,1 . 8,31 . 300 . ln (2,46/1,23) = 173 J
Q = W = 173J
∆U = 0 (não há variação de temperatura)
Processo BC: (Volume Constante)
W = 0 (Não realiza Trabalho)
Q = nCv∆T = 0,1x12,5x300 = 375J
∆U = nCv∆T -W = 375J
Processo CA: (Pressão Constante)
W = nR∆T = 0,1x8,31x300 = - 249J (O trabalho será negativo pois o volume diminui)
Q = 0,1x(2,5)x(8,31)x300 = -623J
∆U = 623 – 249 = -374J
7 – 1 g de gás hélio, com CV = (3/2)R, inicialmente nas condições NTP, é submetida aos
seguintes processos: (i) Expansão isotérmica até o dobro do volume inicial; (ii)
Aquecimento a volume constante, absorvendo 50 cal; (iii) Compressão isotérmica, até
voltar ao volume inicial.
a) Represente os processos no plano (P, V), indicando P (em atm), V (em l) e T
(em K) associado a cada ponto.
b) Calcule ∆U e ∆W para os processos (i), (ii) e (iii).
6
ComSizo.blogspot.com
Capítulo - 9
AB: p1V1 = p2V2
1V0 = p2 x 2V0
P2 = 0,5 atm
Processo AB:
∆U = 0 (não há variação de temperatura)
W = Q = n.Cv.∆T = 393 J
Processo BC: (Volume constante)
∆W = 0
∆U = Q = nCv∆t = 209 J
Processo CD: (transformação isotérmica)
∆U = 0
W = Q = n.Cv.∆T = -490 J
7
ComSizo.blogspot.com
Capítulo - 9
8 – Um mol de um gás ideal descreve o ciclo ABCDA representado na fig., no plano (P,
V), onde T = T1 e T = T2 são isotermas. Calcule o trabalho total associado ao ciclo,
em função de P0, T1 e T2.
Em A:
. / . / / Em B:
. 0 . 0 0 . /
. 0
/
7 789 79: 7@8 0 / . . . ln 1 2 . . . ln 1 2
0
. . /
+ 7 0 / . . . ln 1
2 . . . ln 1
2
. 0
. Logo, o trabalho total é:
9 - Um mol de gás hélio, com CV = (3/2)R, inicialmente a 10 atm e 0°C, sofre uma
expansão adiabática reversível até atingir a pressão atmosférica, como primeiro estágio
num processo de liquefação do gás.
a) Calcule a temperatura final (em °C).
b) Calcule o trabalho realizado pelo gás na expansão.
a) O hélio é um gás monoátomo se Cv = 3/2R então Cp = 5/2R
γ =
Cp
= 5/3
Cv
Dados:
Estado inicial
Pi = 10 atm
Vi = ?
Ti = 0ºC = 273 K
Estado Final
Pf = 1 atm
Vf = ?
Tf = ?
n =11 (nº de mols)
8
ComSizo.blogspot.com
Capítulo - 9
R = 8,3145 J/mol K
γ
PiVi = Pf V f
γ
PiVi = nRTi
Pf V f = nRT f
γ
 Vi

V
 f

P
 = f
P

 i

 Pi

P
 f
 Vi

 V
 f



(A)
  Ti
=
 T
  f




Elevando – se ambos os lados desta expressão pelo expoente γ, temos:
 Pi

P
 f




 Pi

P
 f




 Pi

P
 f




γ
γ
γ
 Vi

V
 f

 
 =  Ti 

T 

 f 
 Pf

 Pi
  Ti
 = 

  Tf
γ −1
T
= i
T
 f
P
T f = Ti  i
P
 f




γ −1








γ
Substituindo A na expressão temos:
γ
γ
χ
Substituindo os dados temos:
 10 
Tf = 273  
1
5 / 3−1
5/3
Tf = 108,7 K = -164,3 ºC
b) O trabalho numa expansão adiabática entre os estados (i) e (f) é:
Wi – f = -nCv (Tf - Ti)
Wi – f = 2045J
9
ComSizo.blogspot.com
Capítulo - 9
10 – 1 l de H2 (para o qual γ = 7/5), à pressão de 1 atm e temperatura de 27°C, é
comprimido adiabaticamente até o volume de 0,5 l e depois resfriado, a volume
constante, até voltar à pressão inicial. Finalmente, por expansão isobárica, volta à
situação inicial.
a) Represente o processo no plano (P, V), indicando P (atm), V (l) e T(K) para
cada vértice do diagrama.
b) Calcule o trabalho total realizado.
c) Calcule ∆U e ∆Q para cada etapa.
V1 = 1 l ; V2 = 0,5 l ; M H 2 = 2 g/mol ; TA = 27°C = 300 K ; P1 = 1 atm
5

C V = 2 R

7
 CP = R
2

7
γ=
5
a) AB:
P1.V1γ = P2 .V2γ
⇒
V2 = 2,64 atm = 2,64 x (1,013 x 105) N/m²
T1.V1γ −1 = T2 .V2γ −1
⇒
TB = 395,85 K ≅ 396 K
P2 P1
=
TB TC
⇒
TC = 149,9 K ≅ 150 K
BC:
b)
W A→ B = −
(P2 .V2 − P1 .V1 ) = − (2,64.1,03.10 5.0,5.10 −3 − 1,013.10 5.1.10 −3 )
γ −1
7 / 5 −1
WA→B = - 81,04 J
WB→C = 0
WC→A = P1(V1 – V2) =1,013.10 5.(1 − 0,5).10 −3 ⇒ WC→A = 50,65 J
WT = -30,3 J
c)
P1.V1
⇒ n = 0,041 mol H2
R.TA
∆UAB = - WA→B (QAB = 0) ⇒
∆UBC = n.CV.(TC – TB)
⇒
∆QCA = n.CP.(TA - TC)
⇒
∆UCA = ∆QCA - WC→A
⇒
n=
∆UAB = + 81 J
∆UBC = ∆QBC = -207,5 J
∆QCA = 177,3 J
∆UCA = 126,6 J
10
ComSizo.blogspot.com
Capítulo - 9
11 - Um mol de um gás ideal, com CV = (3/2)R, a 17°C, tem sua pressão reduzida à
metade por um dos quatro processos seguintes: (i) a volume constante; (ii)
isotermicamente; (iii) adiabaticamente; (iv) por expansão livre. Para um volume inicial
Vi, calcule, para cada um dos quatro processos, o volume e a temperatura finais, ∆W e
∆U.
n = 1 mol ; Pi = 2.Pf ; T1 = 17°C = 290 K.
5

C
=
R
P

3
2
CV = R 
5
2
 γ=
3

(i): Volume constante.
2Pf Pf
=
Vf = Vi
⇒ T2 = 145 K
T1 T2
∆W = 0
∆U = n.CV.(T2 – T1) ⇒ ∆U = -1808,3 J
(ii): Temperatura constante.
2.Pf.Vi = Pf.Vf
∆U = 0
⇒ Vf = 2.Vi
 2.Vi 

∆W = n.R.T. ln
 Vi 
(iii): Adiabático.
⇒
∆W = 1671 J
(2.Pf ).Viγ = Pf .Vfγ
⇒
Vf = 1,52 Vi
T1.Viγ −1
⇒
T2 = 219,4 K
=
T2 .Vfγ −1
∆Q = 0
∆U = - ∆W ⇒ n.CV.∆T
∆W = + 885 J
⇒
∆U = - 885 J
(iv): Expansão livre.
2.Pf.Vi = Pf.Vf
T2 = T1
∆Q = 0
∆U = 0
∆W = 0
⇒ Vf = 2.Vi
12 - No método de Rüchhardt para medir γ = Cp / Cv do ar, usa-se um grande frasco
com um gargalo cilíndrico estreito de raio a, aberto para a atmosfera (p0 = pressão
atmosférica), no qual se ajusta uma bolinha metálica de raio a e massa m. Na posição de
equilíbrio O da bolinha, o volume de ar abaixo dela no frasco é V (fig.).
a) Calcule a força restaurador a sobre a bolinha quando ela é empurrada de uma
distância x para baixo a partir do equilíbrio, o movimento sendo suficientemente rápido
para que o processo seja adiabático. Mostre que a bolinha executa um movimento
harmônico simples e calcule o período τ em função de a, m, V, p0 e γ.
11
ComSizo.blogspot.com
Capítulo - 9
b) Numa experiência em que a = 0,5 cm, m = 10 g, V = 5 l, p0 = 1 atm, o período
observado é τ = 1,5 s. Determine o valor correspondente de γ para o ar.
13 - Um mol de um gás ideal, partindo das condições NTP, sofre: (i) uma compressão
isotérmica até um volume de 5 l, seguida de (ii) uma expansão adiabática até retornar ao
volume inicial, atingindo uma pressão final de 0,55 atm.
a) Calcule P ao fim da etapa (i) e T ao fim de (ii).
b) Calcule Cp e Cv para este gás.
c) Calcule a variação total de energia interna.
d) Calcule o trabalho total realizado.
Na CNTP, temos:
Vo=22,4L; Po=1atm; To=273K
a) Analisando i:
T=To; V=5L
. . Analisando ii:
V`=22,4L; P`=0,55 atm; W= - ∆U
1 A 22,4
+ 4,48 3
5
4,48
B
log I
J
logFG`H
`
7
0,55
. B `. `B 1 2 C C
+C
22,4
`
5
log I`G J
log I
J
5
Logo:
B'/
B
`
B'/
` B
` . 1 2
`
B'/
B
` K
'/
,
0,55 K
273. 1
2 ,
4,48
+ L 150M
5
RS + RS 7G 1
C1
2
U
5
PRT
5 7
7
O C RT RS . C RT . + RT 2 5
2
NRS
b) Pela relação temos:
Q
O
RS 12
ComSizo.blogspot.com
Capítulo - 9
c) ∆V . RS . ∆ ∆V 1. . 8,314. 150 273 + ∆V 2557?
,
0
d) Trabalho total é igual à soma dos trabalhos de i e ii. Logo:
Z
1
7W ∆V . . . X . Y 7W ∆V . . . ln 1 2 Z[ 5
7W 2557 1.8,314.273. ln 1
2 + 7W 847?
22,4
13